Объем призмы. Объем призмы как найти

Объем граненой пирамиды равен произведению высоты h(os) на сумму высот s₁(ABCDE), нижнее основание пирамиды огранки₂ (abcde) и среднее между ними.

Объем четырехугольной призмы: как вычислить, формулы и примеры

Рассмотрим, как вычислить объем четырехугольной призмы с видами и примерами.

Стереометрия — важная часть уроков общей геометрии, посвященных свойствам пространственных фигур. Одной из таких форм является четырехугольная призма. В этой статье более подробно рассматривается задача о том, как вычислить объем четырехугольной призмы.

Что собой представляет призма четырехугольная?

Очевидно, что прежде чем дать вид опухоли четырехугольной призмы, необходимо дать четкое определение этой геометрической фигуры. Под такой перспективой понимается трехмерный многогранник, окруженный одновременно двумя произвольно одинаковыми четырехугольниками и четырьмя прямоугольниками.

Четыре параллельные стороны — это дно фигуры, а четыре прямоугольника — боковые стороны. Здесь следует пояснить, что основание не обязательно является прямоугольником, хотя прямоугольники также являются четырехугольниками. Пример неправильного четырехугольника, который может быть основанием призмы, показан на рисунке ниже.

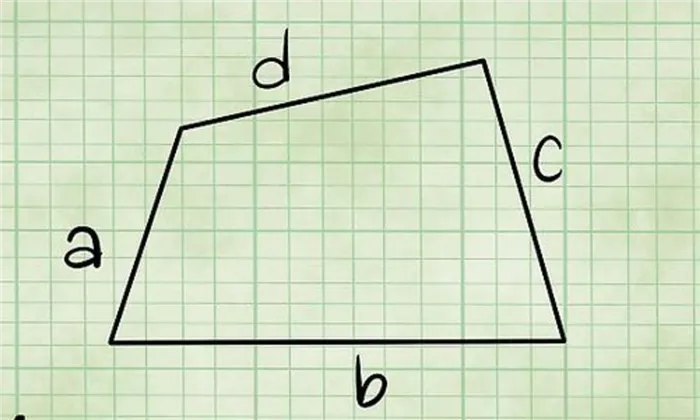
Каждая четырехгранная призма состоит из шести граней, восьми вершин и 12 ребер. Существует несколько типов четырех призм. Например, они могут быть угловыми или линейными, нерегулярными или нормальными. В следующей статье показано, как рассчитать количество четырехугольных призм с учетом их видов.

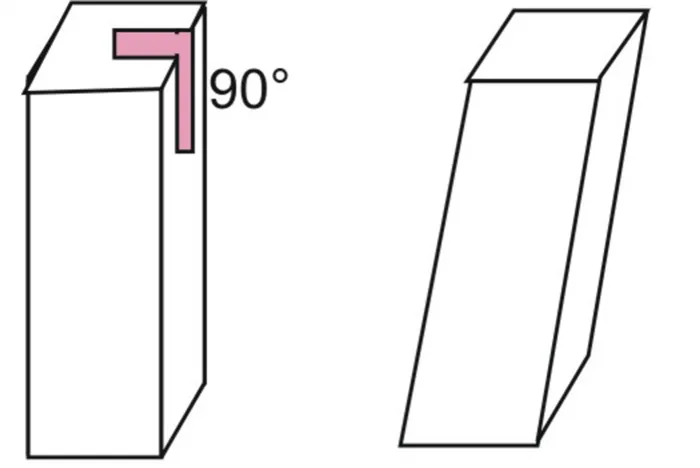
Наклонная призма с неправильным основанием

Поскольку это наиболее асимметричный тип четырехугольной призмы, расчет ее объема относительно сложен. Объем может быть определен по следующим типам

Под символом s_o символизирует площадь основания. Если это основание ромбическое, прямоугольное или продолговатое, вычислите s_o Расчет прост. Таким образом, для ромбических и прямоугольных применяется тип

где a — сторона основания, h_a — падает с вершины основания — это длина высоты.

Если основанием является неправильный многоугольник (см. выше), его площадь нужно разделить на более простые фигуры (например, треугольники) и найти общую сумму путем вычисления площади.

Для объемных типов символ обозначает высоту призмы. Это длина вертикального участка между двумя основаниями. Поскольку призма наклонная, высота рассчитывается с помощью длины боковой кости B между гранями и основанием и двойного угла.

На чертеже видно, что стороны состоят из четырех равных прямоугольников. Их площадь рассчитывается как произведение периметра основания на высоту фигуры.

Формулы вычисления объема правильной призмы

Существуют различные типы подходящих призм, в зависимости от многоугольников основания. Тип расчета объема одинаков во всех случаях.

Внимание. Если преподаватель обнаружит плагиат в вашей работе, серьезных проблем не избежать (вплоть до выкидыша). Если вы не можете написать свой собственный, вы можете заказать его здесь.

Единственное различие заключается в том, как расположены S-области каждой фигуры.

Треугольная

Чтобы вычислить объем прямоугольного треугольника по его основанию, используйте следующие типы

где DŽ (DŽ frac4 \ cdot a^2 = s \) — площадь прямоугольного треугольника при его основании, a — сторона треугольника, h — высота общей фигуры.

Четырехугольная

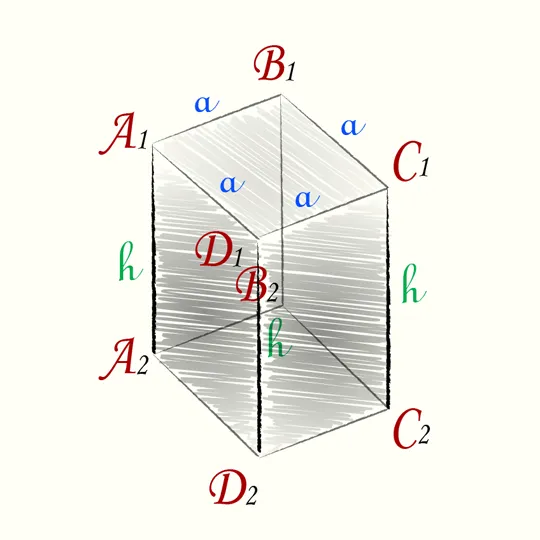
Для квадратного основания объем вычисляется с помощью следующих типов

Пятиугольная

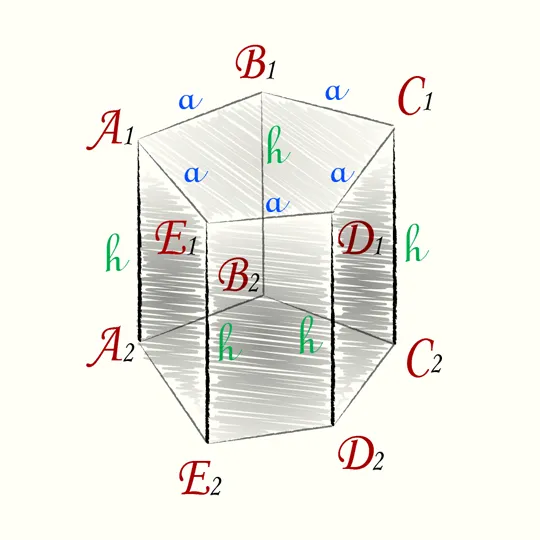
В этом случае объем рассчитывается в соответствии с типом.

Шестиугольная

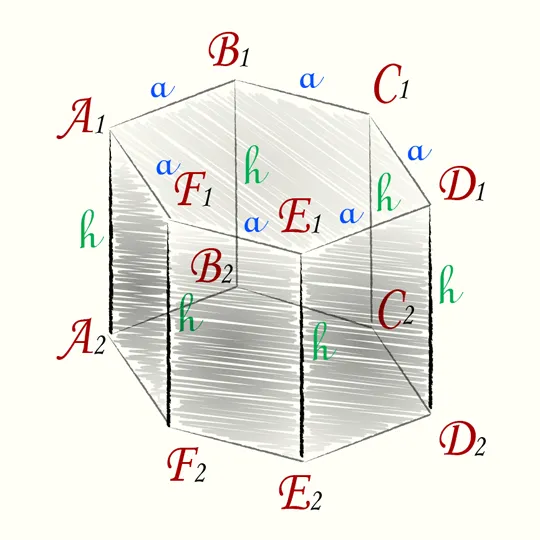
Для призм с правильным шестиугольником в основании тип опухоли следующий

Объем наклонной и прямой

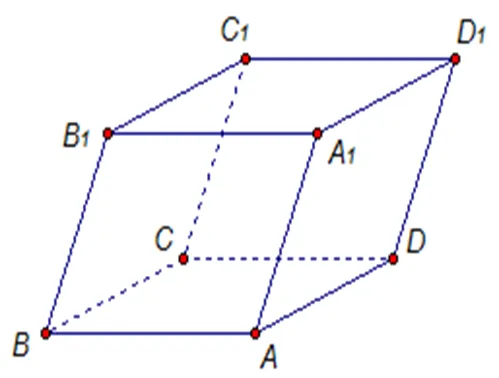
Его можно найти, умножив площадь основания на высоту: основание — это площадь призмы.

Поэтому формула для расчета объема такая же, как и для предыдущего варианта, и зависит только от формы основания.

То же самое относится и к прямым призмам. Сначала вычисляется площадь основания, затем она умножается на высоту.

Примеры задач

Известно, что площадь основания призмы равна 12 Ј (см ^ 2 \), а ее длина 5 см. Вычислите объем фигуры.

Площадь основания уже задана, поэтому форма основания не имеет значения. Замените известные значения в уравнении:.

В основании прямой призмы лежит четырехугольник со сторонами α и β 6 см и 3 см. Высота этой формы составляет 10 см. Вычислите его объем.

Поскольку сначала нам нужно определить площадь четырехугольника и вычислить его объем, мы используем следующее уравнение: Ј(V = a \ cdot b \ cdot h \)

Если основание четырехугольной призмы квадратное, а сама форма прямая, то она называется нормальной призмой. Стоит пояснить, что если все стороны призмы прямоугольные, каждая из которых перпендикулярна основанию, то призма прямая. Схема справа показана ниже.

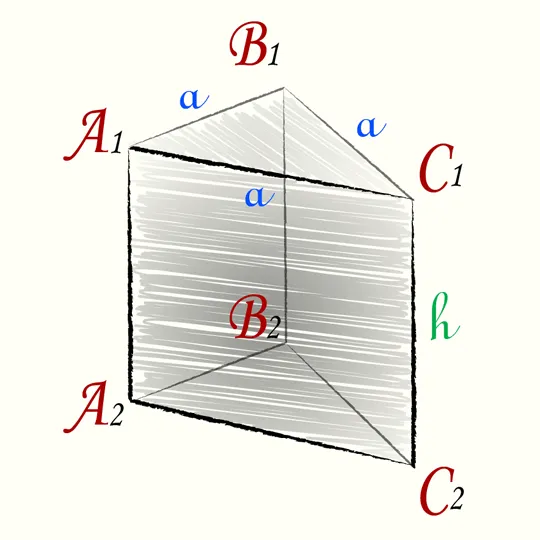
Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ Основание призмы.

Четырехугольник A₁B₁BA, B₁BCC₁ и А₁C₁CA — это стороны призмы.

Стороны грани — это ребра призмы (A₁B₁, A₁C₁, C₁B₁, АА₁, CC₁, BB₁AB, BC, AC), треугольная призма имеет в общей сложности девять сторон.

Высота призмы — это часть вертикальной линии, соединяющей две стороны призмы (h на рисунке).

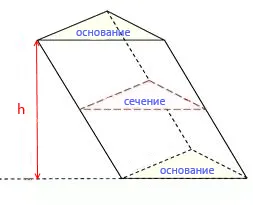
Диагональ призмы — это часть призмы с концами в двух вершинах призмы, которые не принадлежат одной стороне. Треугольная призма не может иметь такую диагональ.

Площадь основания равна площади треугольной грани призмы.

Сторона призмы равна сумме площадей квадратных поверхностей призмы.

Объем правильной фигуры через значение ее диагонали

Поскольку треугольная призма является самой простой фигурой в этом классе, она имеет только один тип диагонали. Это диагонали трех прямоугольников.

Предположим, что у нас есть правильная форма с диагональю d (прямоугольная диагональ) и высотой h. Как вычислить его объем?

Во-первых, необходимо определить стоимость базовой стороны. Для этого используйте теорему Пифагора.

Тогда формула для объема треугольной призмы принимает вид

V = √3/4 x a2 x h = √3/4 x (d2 —h2) x h

Для нормальной призмы объем всегда является функцией двух параметров (h и d в данном уравнении).

Вычисление объема правильной пятиугольной призмы

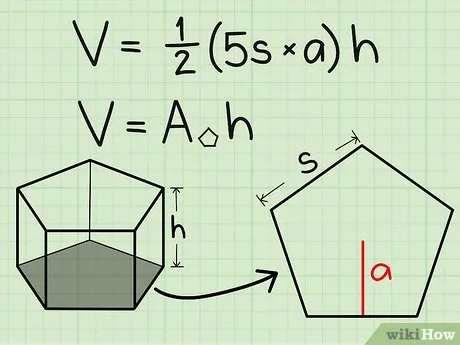
Напишите уравнение для объема пятиугольной призмы. Формула такова: v=1/2x5x сторона пятиугольника x запас x высота призмы. Используя первую часть уравнения, вы можете найти площадь пятиугольника в основании призмы. Это можно представить как нахождение областей пяти треугольников, составляющих правильный пятиугольник. В этом случае стороны пятиугольника равны основанию треугольника, а делитель равен высоте треугольника. Умножьте эти величины на 1/2, чтобы найти площадь треугольника, и умножьте результат на 5. Это происходит потому, что пять одинаковых треугольников образуют основание правильной пятиугольной призмы. 4

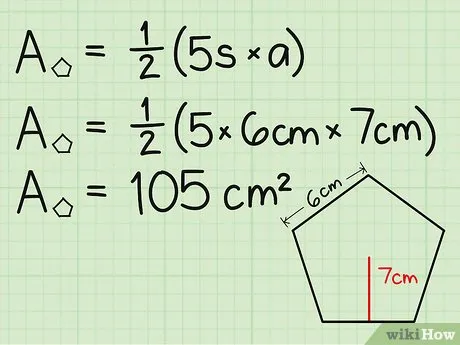
Найдите площадь основания пятиугольника. Предположим, что длина одной стороны равна 6 см, а длина другой — 7 см. Просто замените эти элементы в формуле.

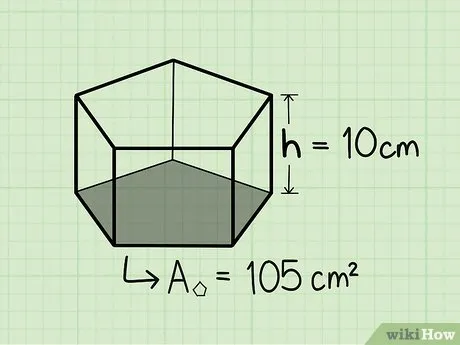
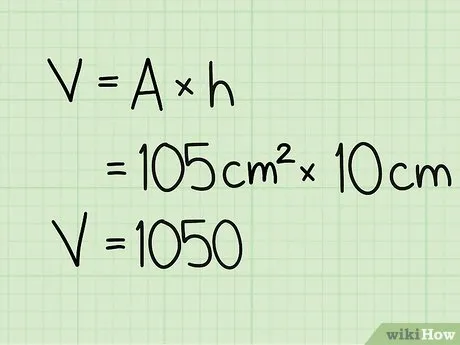
Умножьте площадь основания пятиугольника на высоту призмы. Умножьте площадь основания (105 см 2 ) на высоту (10 см), чтобы найти объем правильной пятиугольной призмы.

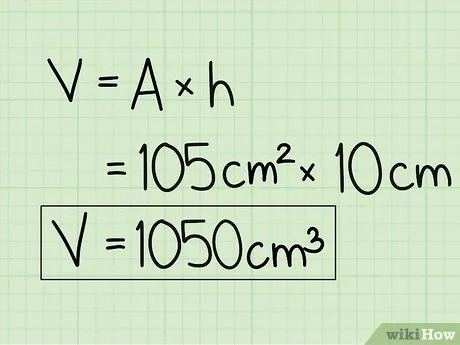
Цена высоты треугольника HA вытекает из того, что противоположное основание также является интерстициальным и дихотомическим. Таким образом, площадь SO является функцией только одного параметра (сторона A).

Объем усеченной пирамиды

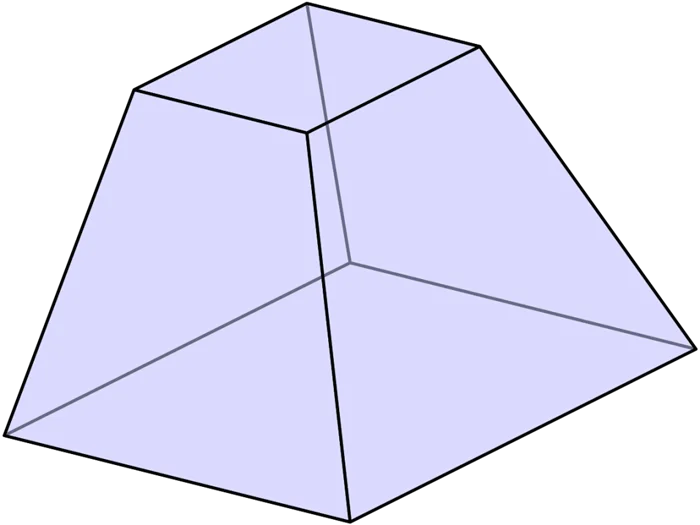
Объем граненой пирамиды равен произведению высоты h(os) на сумму высот s₁(ABCDE), нижнее основание пирамиды огранки₂ (abcde) и среднее между ними.

Тип среза пирамиды объем:.

S1 — площадь вершины разрезанной пирамиды, S2 — площадь основания разрезанной пирамиды, H — высота разрезанной пирамиды.

Объем цилиндра

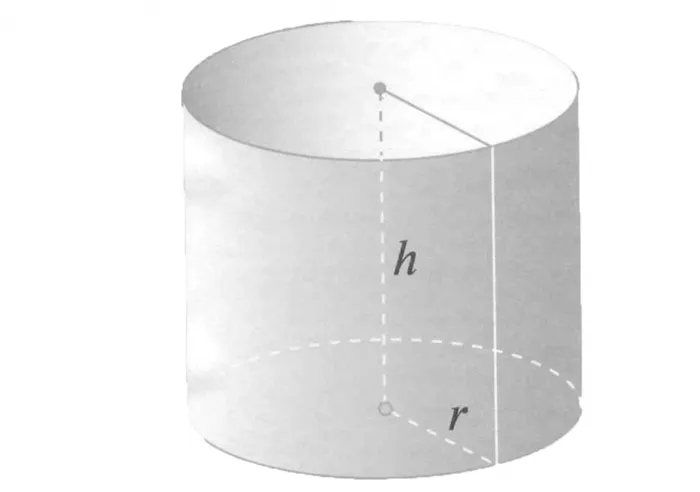
Объем цилиндра равен произведению основания основания на высоту основания.

Вид объема цилиндра: v =πr2 h v = s h

v — объем цилиндра_o — площадь основания цилиндра, r — радиус цилиндра, h — высота цилиндра, π = 3,141592

Объем правильной треугольной пирамиды

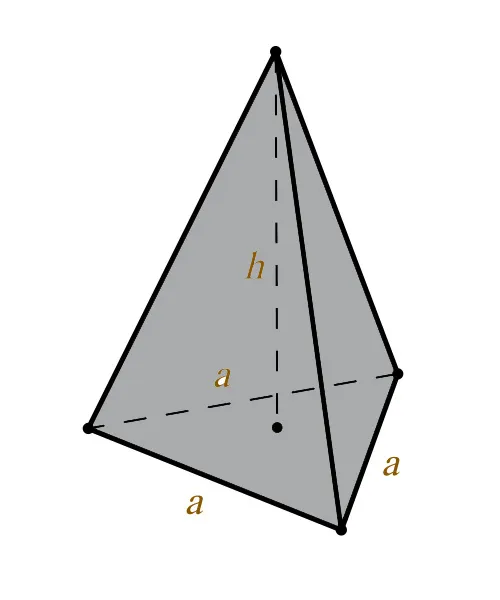
Объем нормальной треугольной пирамиды равен одной трети произведения нормального треугольника, основание которого S (ABC) на высоту H (OS).

Вид объема пирамиды из нормальных треугольников следующий

V — объем пирамиды H. Высота пирамиды A — это сторона основания пирамиды.

Обратите внимание, что если окружность описана вокруг прямоугольного треугольника, то треугольник является ее диаметром, т.е. c = 2r. Поэтому при необходимости тип c можно заменить на (2r).

Объем призмы с равнобедренным треугольником в основании

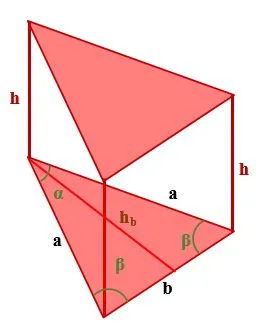
Если треугольник изошеллы находится в основании призмы, то его объем можно найти по следующему виду

Где: v — объем призмы с изоширным треугольником в основании h. _b — Это высота треугольника изошелла и угол между длиной равной стороны треугольника изошелла при основании призмы B — основании треугольника изошелла A — и длиной стороны треугольника изошелла при основании призмы B — основании треугольника изошелла B. Угол между сторонами бигенного треугольника B и основанием — равными сторонами треугольника изохилла при основании призмы B — треугольника изохилла при основании призмы B.

Объем параллелепипеда и куба

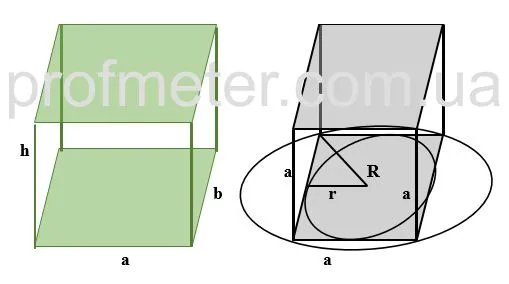
Если основание призмы прямоугольное, то число типов для нахождения количества таких призм также больше.

Где: v — объем призмы в основании, на котором расположен прямоугольный VC. Высота куба h — это высота призмы, описанной вокруг основания куба r. Куб.

Плоскость, параллельная боковой грани, проходит через среднюю линию основания треугольной призмы. Объем разрезанной треугольной призмы равен 5. Найдите объем исходной призмы.

Объем прямых призм

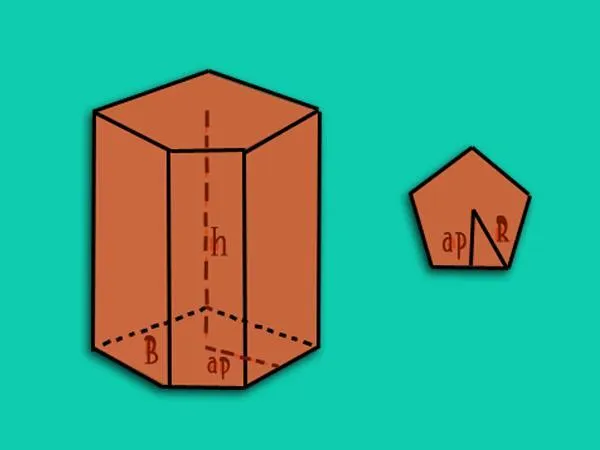
Сразу же отметим, что не существует общего вида для вычисления объема прямоугольной призмы, приведенного выше для нормальной призмы. Для нахождения этого количества необходимо использовать исходную формулу.

Как и в предыдущем случае, это длина внешнего прыща. Что касается базовой площади, то здесь могут быть получены различные значения. Задача вычисления прямой призмы — найти площадь ее основания.

Поэтому он должен рассчитываться исходя из особенностей самой базы. Например, для треугольника площадь можно вычислить следующим образом

где HAP — божественность треугольника, т.е. высота треугольника, падающая на основание A.

Если основание четырехугольное, это может быть стол, прямоугольник, прямоугольник или вообще любой тип. Во всех упомянутых случаях для определения площади используется соответствующий тип планеты. Например, в случае со столом у этого человека есть форма.

Здесь HA — высота трапеции, а A1 и A2 — длины ее параллельных сторон.

Чтобы определить площадь многоугольников высшего класса, необходимо разделить их на простые фигуры (треугольники, четырехугольники) и вычислить сумму последних.

Объем наклонных призм

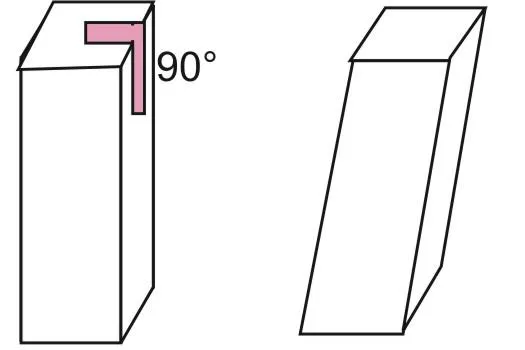
Это самый сложный случай вычисления объема призмы. К этим предметам также применимы общие типы.

Однако, если трудно найти площадь основания, представляющего какой-либо тип, возникает дополнительная проблема определения высоты фигуры. Она всегда короче длины внешнего пупырышка наклонной призмы.

Проще всего найти эту высоту, если известен угол наклона фигуры (ровный или двугранный). Если дан такой угол, используйте его для построения прямоугольного треугольника в свету, одной из сторон которого является высота H, и найдите значение H, используя тригонометрические функции и теорему Пифагора.

Геометрическая задача на определение объема

Дана обыкновенная призма с треугольным основанием длиной 14 см и высотой 5 см. Каково количество треугольной призмы?

Поскольку мы говорим об обычной схеме, мы вправе использовать привычный тип. У нас есть:.

v3 = 3/4*a2*h*ctg(pi/3) = 3/4*52*14*1/√3 = √3/4*25*14 = 151,55 см3.

Треугольные призмы имеют достаточно симметричную форму, из них часто строят различные архитектурные сооружения. Эта стеклянная призма используется в видовых точках.

Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоской поверхностью. Его название зависит от формы его основания. Например, если она треугольная, то призму называют «треугольной».

Площадь поверхности и объём

Чтобы найти объем призмы, необходимо знать ее основание и площадь ее высоты.

Поскольку основанием нормальной четырехгранной призмы является квадрат со стороной A, тип можно записать более подробно.

Если речь идет о кубе, который представляет собой нормальную призму равной длины, ширины и высоты, то объем рассчитывается следующим образом

Чтобы понять, как найти стороны призмы, нужно представить себе конструкцию призмы.

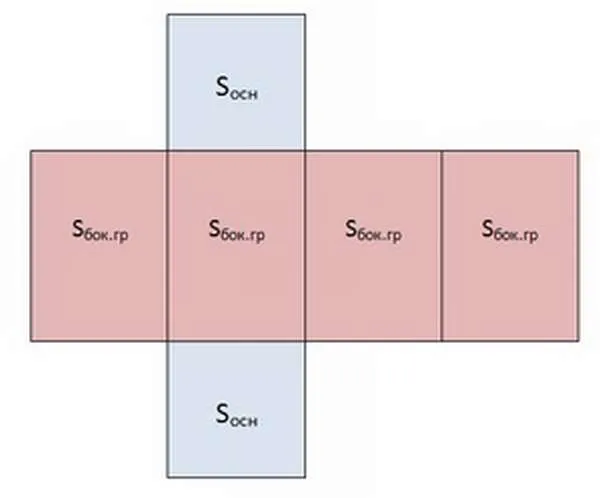
На чертеже видно, что стороны состоят из четырех равных прямоугольников. Их площадь рассчитывается как произведение периметра основания на высоту фигуры.

Так как периметр квадрата равен p = 4a, то вид имеет вид

Чтобы вычислить общую площадь призмы, к двум площадям основания прибавляют площадь боковых сторон.

Для четырехугольной призмы формула имеет вид

Для поверхности куба:.

Зная объем или поверхность, можно вычислить отдельные элементы геометрического тела.

Нахождение элементов призмы

Часто возникают проблемы, когда известен объем или площадь стороны, а нужно определить длину основания или высоты. В таких случаях можно извлечь уравнение.

• длина стороны основания: a = Sбок / 4h = √(V / h),
• длина высоты или бокового ребра: h = Sбок / 4a = V / a²,
• площадь основания: Sосн = V / h,
• площадь боковой грани: Sбок. гр = Sбок / 4.

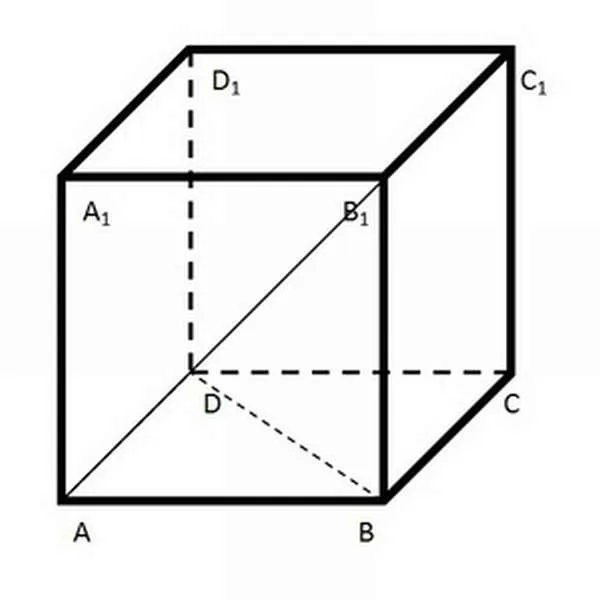
Чтобы определить площадь диагонали, нужно знать длину диагонали и высоту фигуры. В случае квадрата, d =a√2. Отсюда следует, что: d =a√2.

Этот тип используется для вычисления диагонали призмы.

Чтобы понять, как применять указанные пропорции, можно потренироваться и решить несколько простых задач.

Примеры задач с решениями

Некоторые из задач, представленных на выпускном экзамене по математике, перечислены ниже.

Коробка, имеющая форму правильной квадратной призмы, заполнена песком. Его уровень составляет 10 см в высоту. Каков будет уровень песка, если его пересыпать в контейнер той же формы, но с основанием в два раза длиннее?

Обоснование следующее. Количество песка в первом и втором контейнерах не изменилось, т.е. объем песка в них одинаков. Мы можем обозначить длину основания через a. В этом случае для первой коробки объем вещества составит:

Для второго ящика длина основания равна 2a, но высота уровня песка неизвестна:

Поскольку V₁ = V₂, мы можем приравнять эти выражения:

После уменьшения обеих частей уравнения на a² получаем:

В результате новая плоскость песка будет иметь размер h = 10 / 4 = 2,5 см.

ABCDA₁B₁C₁D₁ — правильная призма. Известно, что BD = AB₁ = 6√2. Найдите общую площадь поверхности тела.

Чтобы было легче понять, какие элементы известны, рисунок можно реконструировать.

Поскольку речь идет о правильной призме, можно сделать вывод, что в основании лежит квадрат с диагональю 6√2. Диагональ боковой грани имеет ту же величину, поэтому боковая грань также имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина каждого ребра определяется известной диагональю:

Общая площадь находится по формуле для куба:

В комнате идет ремонт. Известно, что его пол представляет собой квадрат площадью 9 м². Высота помещения 2,5 м. Помещение представляет собой квадрат с планировкой 9 м. Какова минимальная стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Учитывая, что пол и потолок квадратные, то есть нормальные четырехугольники, а стены перпендикулярны горизонтальным поверхностям, можно сделать вывод, что это нормальная призма. Необходимо определить площадь его боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обои будут покрывать площадь S сторон = 4-3-2,5 = 30 м².

Минимальная стоимость обоев для этой комнаты составит 50-30 = 1500 рублей.

Таким образом, для решения задач о прямоугольной призме достаточно знать, как вычислить площадь и периметр квадрата и прямоугольника, а также иметь формулы для нахождения объема и площади.