Двузначное натуральное число — это натуральное число, записанное с помощью двух знаков (двух цифр). Используемые числа могут быть одинаковыми или разными.
Натуральные числа
Натуральные числа и различные системы их представления восходят к древним цивилизациям, таким как Древняя Месопотамия, Древний Египет, Древний Китай и племена майя. Концепция числа «ноль», по-видимому, появилась позже, чем поздние вавилонские и майянские представления о натуральных числах.
В древние времена палочки использовались для счета. Этот символистский метод сохранился в римском исчислении. Число в этой нотации — это сумма или разность баров, записанных без точек.
По мере развития нотации некоторые числа представлялись буквами алфавита. В современных системах счисления значение каждой цифры в числе определяет ее положение в числе. Первыми такими системами обозначений были вавилонская (шестнадцатеричная) и индийская (десятичная).
Вариантом индийской десятичной системой счисления является современная арабская система с тем различием, что в индийской системе отсутствовал ноль. Цифру
Натуральные числа. Множество натуральных чисел
Натуральные числа 400, 2, 3 и ⌘ точка $ используются для нумерации (одна груша, две груши, три груши и т.д.) или для обозначения порядкового номера предмета в пределах аналогичного.
Натуральные числа принято записывать с помощью арабских цифр:
Ноль как натуральное число
В русской литературе принято исключать нуль из числа натуральных чисел (
Аксиомы Пеано для натуральных чисел
Множество $N$ называется множеством натуральных чисел, если N$ имеет 400 섹 элементов и N$ имеет функцию последовательности $S:N \ в N$, такую, что выполняются следующие условия.
400 \ в N $: единицы измерения — натуральные числа.
$ x \ в N $, $ S \ слева (x \ справа)\ в N $: если число является натуральным, то следующее число также является натуральным>.
$ \ не существует x \ в N \ слева (S \ слева (x \ справа) = 1 \ справа)$: не существует натурального числа до 1>.
$ S \ слева (b \ справа) = a$ и $S ∈ S ∈ S ∈ S ∷ слева (c \ справа) = a$, то $ b = c$: если за натуральным числом $a$ следует число $b$ и число $c$, то $ b =c$.
Аксиома индукции. Пусть $ P \ слева (n \ справа)$ — единственный предикат, зависящий от натурального числа $n$. Итак.
$ P \ слева (1 \ справа)$ и $\ для всех n{ слева (P \ слева (n \ справа)$ Длинная стрелка P \ слева (S \ слева (n \ справа)$, для $ \ всех n{ P \ слева (n \ справа)$:.
Если высказывание $P$ истинно для $n=1$ и для каждого $n$ истинность $P\ слева (n \ справа)$ следует из истинности $P\ слева (n + 1 \ справа)$, то $P\ слева (n \ справа)$ истинно для любого натурального $n$.
Все аксиомы отражают понятия физического порядка и числовых линий.
($P \ не в N $), а множество нулевых натуральных чисел обозначается $N_0$.
В международной математической литературе множество $ \ левых \ $ обычно называют множеством целых положительных чисел и обозначают $Z+$. Множество $\left \ $ обычно называют множеством целых неотрицательных чисел и обозначают $Z.<\ge 0>$.
Чтобы прочитать натуральные числа, сделайте следующее.
Разделите числа на группы по $ 3 $ цифр справа налево.
Прочитайте группы по $ 3 $ в порядке слева направо и добавьте название класса.
Если группа цифр состоит из одних нулей, имя класса опускается.
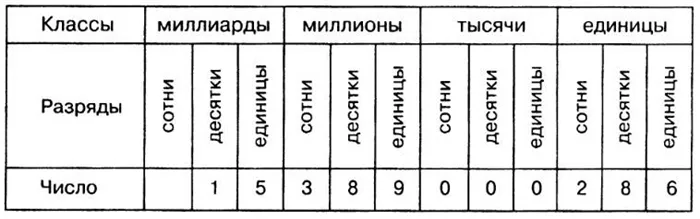
Каждая цифра класса называется цифрой класса.
Наименьшее натуральное число — это число, используемое в первой половине перечисления. Например, цифра $9$ меньше, чем $20$ (запишите $9 55$).
1, 2, 3, 4, 5, 6, 7, 8, 9$.

Готовые работы на аналогичную тему
Натуральное число (или натуральное число) — число, которое появляется естественным образом при измерении чего-либо.
Натуральные числа: $3, 48, 157, 1089, $25556.
Все натуральные числа, расположенные в порядке возрастания, образуют ряд натуральных чисел.
Существует два подхода к определению натуральных чисел
Числа, полученные в результате счета (нумерации) объектов (например, первый, второй и т.д.).
Числа, используемые для обозначения количества объектов (нет стула, стул, два стула и т.д.).
В первом подходе натуральные числа начинаются с единицы, а во втором — с нуля.
Математики не пришли к единому мнению о том, следует ли считать ноль натуральным числом. В большинстве российских источников первый подход является традиционным. Второй подход широко используется при планировании (например, индекс RAIDS, номера битовых кодов и т.д.).
Натуральные числа не включают отрицательные или нецелые числа.
Сумма всех натуральных чисел обозначается $ n = \ левое \ $ и характеризуется бесконечностью. Это объясняется тем, что каждое вещественное число $ n $ имеет натуральное число большее, чем $ n $.
Какое из этих чисел является натуральным числом?
)
Ответ: $ 5; \ \ \ \ \ 38; \ \ \ \ \ \ ну 4.
Для формулировок и доказательств многих теорий натуральных чисел удобно использовать ноль, поэтому в первом подходе используется понятие расширенного множества натуральных чисел, включающего ноль, обозначаемого $ n_0 $ или $ z_0.
Он был изобретен арабами, после чего система нумерации приняла свой современный вид.
Час стоит $160 (из расчета $60): $400 за час включает 60 минут; 400 минут включает 60 секунд.
Работа Пьера де Ферма была заложена как отдельная наука, включающая изучение чистых и типичных свойств натуральных чисел, основанная на фундаменте теории чисел или хорошей арифметики.
Теоретико-множественное определение натуральных чисел (определение Фреге—Рассела)
Согласно теории множеств, единственным объектом построения математической системы является целое.
Поэтому, исходя из концепции целого, натуральные числа вводятся в соответствии с двумя правилами.
Числа, приведенные таким образом, называются нормальными или обычными числами.
Первые нормальные числа и соответствующие им натуральные числа описываются следующим образом
Кроме того, есть и другие цифры. Например, в информатике используется двоичная система. При измерении времени используется шестнадцатеричная система символов.
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел уходит корнями в доисторические времена. С древних времен люди считали вещи. Например, торговля требовала подсчета товаров и строительных материалов. Даже в повседневной жизни людям приходилось считать предметы, еду и животных. Первоначально числа действительно использовались только для счета в жизни, но позже, с развитием математики, они стали частью науки.
Натуральные числа — это числа, которые мы используем для измерения вещей.
Примеры: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,.
Ноль не упоминается в натуральных числах.
Назовем все натуральные числа, или множества натуральных чисел, обозначаемые символом n.
Таблица натуральных чисел.
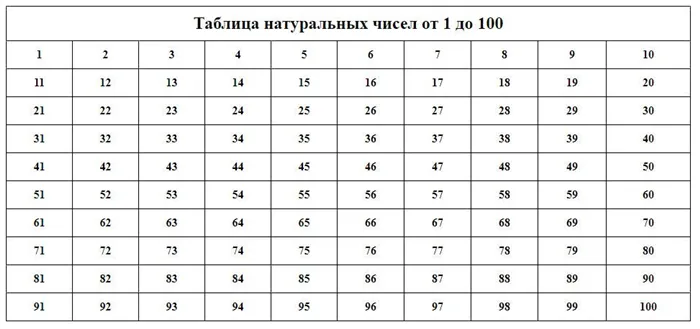
Натуральный ряд.
Натуральные числа, записанные последовательно в порядке возрастания, представляют собой серию натуральных чисел или набор натуральных чисел.
Свойства ряда натуральных чисел:.
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример №1: Напишите первые пять физических чисел. Решение: натуральные числа начинаются с единицы. 1, 2, 3, 4, 5.
Пример №2: Является ли натуральное число нулем? Ответ — нет.
Пример № 3: Каково первое натуральное число? Ответ: натуральные числа начинаются с единицы.
Пример № 4: Каково последнее натуральное число? Какое самое большое физическое число? Ответ: натуральные числа начинаются с единицы. Последнего числа не существует, потому что каждое следующее число больше предыдущего. Большинство чисел не существует.
Пример 5: Имеет ли одно из натуральных чисел предыдущее число? Ответ: нет, потому что единица — это первое число в ряду натуральных чисел.
Пример № 6: Назовите следующее число в ряду натуральных чисел после числа: а) 5, б) 67, в) 9998. ответ: а) 6, б) 68, в) 9999.
Пример № 7: Числа в натуральном порядке между числами: а) 1 и 5; б) 14 и 19. Решение: а) 1, 2, 3, 4, 5 — три числа находятся между числами 1 и 5. б) 14, 15, 16, 17, 18, 19 — четыре числа находятся между числами 14 и 19.
Пример числа 8: Назовите предыдущее число после числа 11. Ответ: 10.
Пример № 9: Какое число используется для подсчета предметов? Ответ: натуральные числа.
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
Деление дробей. Правила. Примеры.
Множественные натуральные числа — это натуральные числа, для записи которых используются два или более символов. Множественные натуральные числа бывают двухзначными, трехзначными и т.д. Цифры.
Сравнение натуральных чисел
В системе позиционирования количественный эквивалент каждой цифры зависит от ее положения в коде номера. Это означает, что числа можно сравнивать по одной цифре за раз, добавляя ведущий ноль одинаковой длины.
При сравнении натуральных чисел необходимо проверить количество цифр в каждом числе. Наибольшая цифра — это цифра с наибольшим количеством знаков. Если числа имеют одинаковое количество цифр, сравнивайте их слева направо. Числа с другой первой цифрой больше, чем остальные цифры.
Разряды натурального числа, значение разряда
Элементами базового или фундаментального числа в десятичной системе счисления являются степени 10: 10 = \ (10 ^ 1 \), 100 = \ (10 ^ 2 \), 1000 = \ (10 ^ 3 \).
Каждая позиция цифры в числе называется числительным, при этом первая цифра слева обозначает число, умноженное на 10. Самая маленькая цифра справа, крайняя правая цифра, является единицей измерения, далее справа налево следуют десятки, сотни, тысячи и т.д. 105 показывает, что 1 — это число сотен, 0 — число десятков и 5 — число единиц.
Арифметические действия над натуральными числами
Арифметические операции включают
Как и при решении других арифметических выражений, последовательность действий следующая. Сначала выполняются операции внутри или вне скобок, сначала умножение и деление, затем сложение и вычитание.
Результат сложения и умножения натуральных чисел во всех случаях является натуральным числом. Можно сказать, что все они замкнуты в терминах сложения и умножения. Операции над элементами серии не дают результата.
Вычисление и деление не обязательно приводят к натуральным числам.
Кроме того, их сложение и умножение являются заместительными и коррелятивными. Это означает, что все элементы формул для этих операций могут быть сдвинуты друг к другу или сгруппированы с помощью круглых скобок.
Самый простой способ найти произведение однозначных натуральных чисел — использовать умножение девяносто девять. Для ускорения вычислений многозначные числа представляются в виде цифровых сумм данных.
Умножение 732 на 10 можно выразить как сумму 700 + 30 + 2.
Формула выглядит следующим образом.
Используя комбинированные свойства умножения, формула приобретает вид
Фактор натурального числа — это функция, определяемая набором неотрицательных целых чисел, которые являются произведением всех натуральных чисел от 1 до названного числа.
Коэффициенты обозначаются восклицательным знаком после числа. Коэффициент 4 записывается как 4! Оно равно 1 x 2 x 3 x 4 = 24.
Если число записано с нулем, оно называется «нулем». Обратите внимание, что ноль не является натуральным числом, но может обозначать его отсутствие. Ноль в объекте означает отсутствие.
Натуральные числа с нолями
С одной стороны, оказывается, что 0 не является натуральным числом. Но кажется естественным спросить: является ли 10 натуральным числом? Конечно, это число и любое другое число с бесконечным числом нулей относятся к этой формуле, поскольку они могут быть использованы для счета или перечисления.
Действия, которые могут выполняться над натуральными числами
Над натуральными числами можно производить различные математические операции.
- Сложение. Два или более чисел являются слагаемыми, а результат действия называется суммой: 345 + 1 813 = 2 158
- Вычитание. Первое число, называемое уменьшаемым, должно быть больше другого, которое именуют вычитаемым. В результате получаем разность: 455 — 120 = 335
- Умножение. Два или более множителей, а в результате получается произведение: 36 х 3 = 108
- Деление. Первое число, которое будет делиться, называют делимым, второе – делителем, а результат – частным. Может быть с остатком или без него: 450:15=30, 450:20=22 + остаток 10.
Существует также порядок натуральных чисел, символика которого такова: ab, где a — основание порядка, а b — экспонента. Например, 3 2 = 9.
Разряды и натуральные числа
Разряд — это точка, в которой число находится в пределах цифры. Каждая цифра называется отдельно и располагается в порядке старшинства (справа налево, от низшей к высшей). Количество цифр в числе соответствует количеству разрядов.
Наименьший значащий разряд равен 1, а старший разряд всегда соответствует крайнему левому разряду.
Например, число 5 469 состоит из четырех цифр.
- 9 – разряд единиц,
- 6 – разряд десятков,
- 4 – разряд сотен,
- 5 – разряд тысяч.
Старшая цифра обозначается как
Цифры сгруппированы по классам, каждый класс содержит три цифры.
Для удобства чтения между классами обычно ставятся пробелы.
Каковы физические ценности математики? Это произвольные величины, представленные рядом натуральных чисел в последовательности. Другой пример: 184 345 567 100 — это число имеет четыре разряда: единицы, тысячи, миллионы и миллиарды.
Каждая позиция цифры в числе называется числительным, при этом первая цифра слева обозначает число, умноженное на 10. Самая маленькая цифра справа, крайняя правая цифра, является единицей измерения, далее справа налево следуют десятки, сотни, тысячи и т.д. 105 показывает, что 1 — это число сотен, 0 — число десятков и 5 — число единиц.
Названия некоторых больших чисел
Одна тысяча (1000) — 1 000 (тысяча)
Один миллион (1 000 000) — 1 000 000 (десятки тысяч)
Один миллиард (1 миллиард) — 1 000 000 000 (100 миллионов)
1 триллион (один триллион) — 1 000 000 000 000 000 000 (сто миллиардов)
Рассмотрим цифру 6,000126,754.
Прочитано: 6,0126,754.
В категории миллионов все цифры равны нулю. Поэтому, если 6 000 126 754 читается: 6 000 126 754, то этот класс имен не произносится.
Значение цифры в записи числа
Важность цифры зависит от ее положения в числе.
Например, в числе 56 97 8 цифра 8 означает 8. Это связано с тем, что он находится в последней позиции (в столбце единиц) записи числа.
При регистрации числа 4238 9 цифра 8 означает восемь десять. Это происходит потому, что он находится во второй позиции от конца записи числа (в десятой позиции).
В записи 53008 47 цифра 8 означает 800. Это происходит потому, что он размещается в третьей позиции от конца числа (вместо сотни).
Число 0 и цифра 0
Число 0 не является натуральным числом.
Число 0 означает, что десятичная часть числа не имеет единиц. Он также используется для обозначения числа «ноль» (что означает «нет»).
(Например, 1:0 в хоккейном матче означает, что другая команда не забила ни одного гола).








