Содержание 1. организация времени 2. разрушение идей 3. зачем нужно уметь измерять и вычислять площадь фигуры 4. не площади 5. площадь прямоугольника 6. д.д. 9. обзор курса 10. домашнее задание 10.
Как найти площадь многоугольной фигуры. Смотреть что такое «Площадь многоугольника» в других словарях
В задачах по геометрии студентов часто просят вычислить площадь многоугольника. Они могут иметь самые разные формы, от привычного треугольника до n -g с немыслимым количеством вершин. Кроме того, эти многоугольники могут быть выпуклыми или полыми. В любом случае, начинать нужно с внешней формы фигуры. Это позволит вам выбрать наилучший способ решения проблемы. Этот показатель может оказаться нормальным. Это значительно упрощает решение проблемы.
При рисовании трех или более пересекающихся линий, образующих фигуру. Это многоугольник. Это видно по количеству перекрестков. Назовите полученное число. Может быть:.
- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такие фигуры обязательно характеризуются двумя позициями.
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются смежными, необходимо проверить, принадлежат ли они одной стороне. Если да, то они являются смежными. В противном случае они могут быть соединены в секции. Их следует называть диагоналями. Они могут быть спроектированы только с помощью многоугольников с тремя или более вершинами.
Какие их виды существуют?
Многоугольники с четырьмя или более углами являются выпуклыми или полыми. Разница с полыми многоугольниками заключается в том, что некоторые из их вершин могут находиться по разные стороны от линии, проходящей через любую сторону многоугольника. У выпуклых многоугольников все вершины всегда находятся по одну сторону от такой линии.
В геометрии средней школы большая часть времени посвящена выпуклым формам. Таким образом, задача заключается в нахождении площади выпуклого многоугольника. Кроме того, существует тип радиуса периметра. Это поможет вам найти необходимое значение для любой заданной формы. В других случаях четкого решения нет. Для треугольников он один и тот же, но для квадратов или таблиц он совершенно другой. Если форма неправильная или имеет много вершин, принято делить их на простые и известные части.
Как поступить, если фигура имеет три или четыре вершины?
В первом случае, который оказывается треугольником, можно использовать один из типов.
- S = 1/2 * а * н, где а — сторона, н — высота к ней;
- S = 1/2 * а * в * sin (А), где а, в — стороны треугольника, А — угол между известными сторонами;
- S = √(p * (p — а) * (p — в) * (p — с)), где с — сторона треугольника, к уже обозначенным двум, р — полупериметр, то есть сумма всех трех сторон, разделенная на два.

Можно доказать, что числа с четырьмя вершинами являются прямоугольными.
- S = а * н;
- S = 1/2 * d1 * d2 * sin(a), где d1 и г2 — диагонали, α — угол между ними;
- S = a * в * sin(α).
Площадь трапеции имеет вид s = n * (a + c) / 2, где a и c — длины оснований.
Объект исследования. Метод исследования: «Грант. Можно предположить, что существует несколько способов найти многоугольники многоугольников на клетчатой бумаге с помощью c.
Через сторону
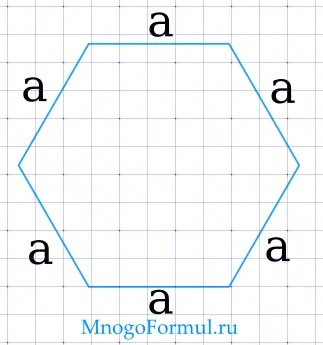
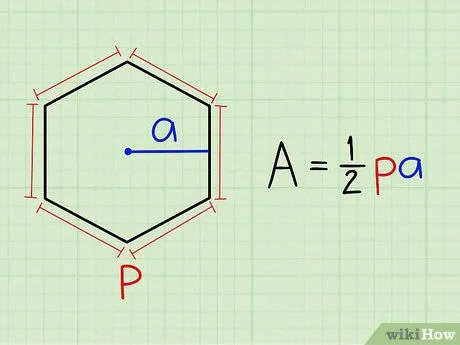
Человек находит область нормальных многоугольников с одной стороны:.
) >>, где a — сторона многоугольника, а n — количество сторон многоугольника.
Через радиус вписанной окружности
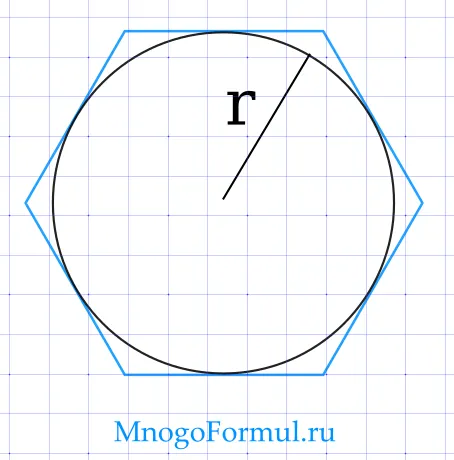
Тип нахождения площади нормального многоугольника через радиус конечного цикла: ) >>, где r — площадь многоугольника через радиус конечного цикла.
) >>, где r — радиус в ячейке, а n — количество сторон многоугольника.
Через радиус описанной окружности
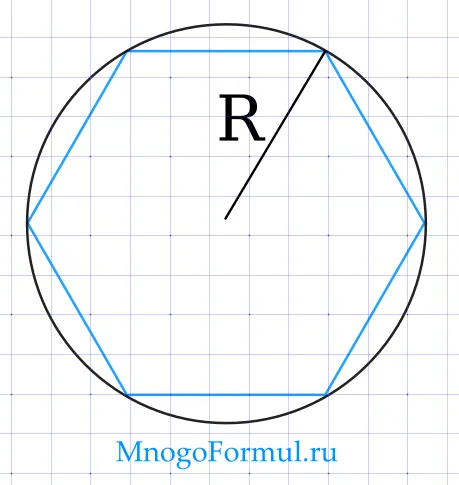
Нахождение площади обычного многоугольника через радиус района:.
\ cdot r^2 \ cdot n \ cdot \ sin(⌘ frac)>, где r — радиус в периферии, а n — число сторон многоугольника.
В большинстве случаев данные смущают тем, что содержат только размер ячейки. Однако никакой дополнительной информации не требуется. Рекомендация для решения таких задач — разделить фигуру на множество треугольников и прямоугольников. Эти площади очень легко вычислить по длинам сторон, которые можно легко суммировать.
Трапеция
Трапеция — это четырехугольник с двумя параллельными и двумя непараллельными сторонами.
S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота стола.
Мы можем построить высоту стола, проведя отрезок так, чтобы он соединял параллельные стороны под прямым углом.
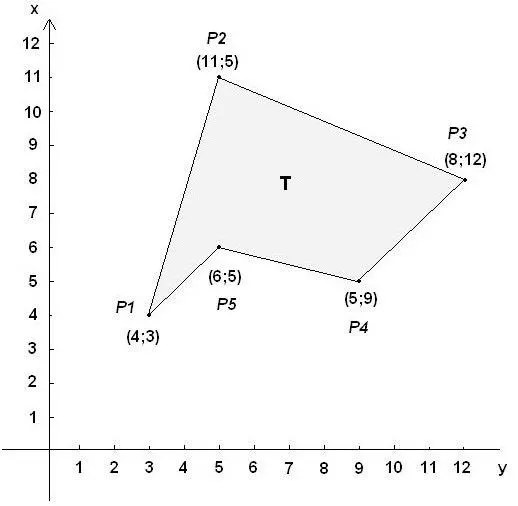
Что делать, если в задаче даны координаты вершин многоугольника?
То есть мы знаем набор пар чисел для каждой точки, которые определяют стороны фигуры. Обычно они записываются как (x1; y1) для первого, (x2; y2) для второй вершины, а n-ая вершина имеет значения (xn; yn)。 Тогда площадь многоугольника определяется как сумма n слагаемых. Каждый из них выглядит следующим образом: ((yi+1 +y私)/2) * (xi+1 — x私)。 В этом выражении i варьируется от одного до n.
Стоит отметить, что знак результата зависит от пересекаемой формы. Если использовать приведенную выше формулу и двигаться по часовой стрелке, то ответ будет отрицательным.
Формула площади прямоугольника
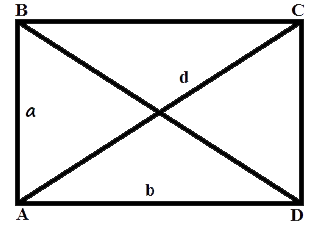
Площадь прямоугольника равна произведению длин двух его смежных сторон
Треугольник — это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных тремя отрезками. Эти три точки называются вершинами, а отрезки — сторонами. Площадь треугольника можно вычислить несколькими способами на основе исходных данных, давайте рассмотрим их.
解決。 В этой задаче нам даже не нужен рисунок. Обозначим высоту через h, тогда основание, которое в два раза длиннее, равно 2h. Произведение этих чисел — площадь, то есть она равна 162:
Понятие площади многоугольника
Понятие площади знакомо нам из повседневного опыта: мы измеряем площадь спортивной площадки или садового участка, используем площадь для расчета количества обоев или коврового покрытия для ремонта комнаты и т.д. Давайте попробуем придать понятию площади определенную математическую строгость.
Под площадью многоугольника будем понимать площадь его внутренней поверхности. Как и в случае измерения длин отрезков, измерение площадей основано на сравнении данной фигуры с фигурой, площадь которой принята за единицу измерения. Единицей площади является площадь квадрата, сторона которого равна единице отрезков.
Например, если за единицу измерения отрезков приняты 1 мм, 1 см или 1 м, то за единицу измерения площади принимают площадь квадрата со стороной 1 мм, 1 см или 1 м. Площадь такого квадрата называется квадратным миллиметром или квадратным метром
При выбранной единице измерения площадь каждого многоугольника выражается положительным числом, которое показывает, сколько раз единица измерения площади и ее части укладываются в данном многоугольнике. Обычно площадь обозначается буквой
Для определения приблизительного значения площади можно использовать палитру — прозрачную пленку с квадратной сеткой (рис. 141).
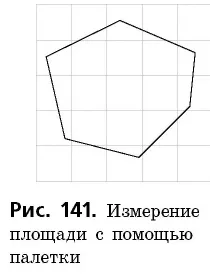
Поместив палетку на фигуру, площадь этой фигуры определяется обычным измерением количества единичных квадратов, которые помещаются в эту фигуру. Однако на практике применение этого метода неудобно. Поэтому для определения площади многоугольника мы обычно измеряем только несколько соответствующих сегментов, а затем вычисляем площадь по соответствующим формулам. Вывод этих формул основан на свойствах площадей, которые мы обсудим ниже.
Прежде всего, отметим, что когда два многоугольника равны, единичная площадь и ее части складываются в каждом из них одинаковое количество раз, т.е. имеет место следующее свойство.
1. Равные многоугольники имеют равные площади.
Далее, пусть многоугольник состоит из нескольких частей — других многоугольников, которые не имеют общих внутренних точек (рис. 142). Если эти части имеют площади то площадь всего многоугольника равна их сумме:

2. Если многоугольник состоит из многих многоугольников, то его площадь равна сумме площадей этих многоугольников.
Третье свойство площадей связано с единицей измерения.
3. Площадь квадрата со стороной, равной единице длины, равна единице площади.
Вышеуказанные три свойства называются аксиомами областей. Таким образом, площадь многоугольника — это положительная величина, числовое значение которой удовлетворяет аксиомам площади.
Из этого, в частности, следует, что каждый многоугольник имеет некоторую площадь, которая однозначно определена в заданных единицах.
意味
Если площади равны, то две фигуры называются равными.
Очевидно, что, согласно первому посту о площади, два равных многоугольника равны. Однако два равных многоугольника не равны.
Рассматривая два равных прямоугольных треугольника (рис. 143а), можно найти равнобедренные треугольники (рис. 143б), прямоугольники (рис. 143в), прямоугольники (рис. 143г) или два смежных четырехугольника, прилегающих друг к другу, один из которых с личиночным доктором (рис. 143e). Все эти формы являются изомерными. То есть, они состоят из одних и тех же многоугольников.
Тип вершины — это настоящее облегчение для студентов, которые не смогли освоить все виды вычислений для расчета областей фигуры, и которые еще не понимают, как делить фигуру или создавать дополнительные структуры. Это приближает их к расчетам в области «известного через скважины».
Формула Пика для вычисления площади многоугольника материал для подготовки к егэ (гиа) по геометрии (9, 11 класс)
В 21 веке некоторые дети могут запомнить огромное количество информации, с которой они каждый день ходят в школу. Во многих случаях о них забывают.
Задача найти площадь многоугольника, изображенного на шашечной бумаге, очень интересна и увлекательна. Что интересного можно найти на уровне пледа, то есть на бесконечном количестве бумаги, на которой преобладают равные квадраты? Вы увидите, что задачи, связанные с клетчатой бумагой, совершенно разные. Мы знаем различные способы выполнения этих задач: методы интегрирования, методы деления и т.д. Одним из таких методов является тип вершины для нахождения площади многоугольника.
Важность этого вопроса заключается в том, чтобы помочь учащимся 9 и 11 классов подготовиться к GCSE и использовать его в математике.

Георг Александр Пик был австрийским математиком. Георг Пик родился в еврейской семье и учился у своего отца, чудо-ребенка и директора частного института. Георг обучался дома (у своего отца) до 11 лет, когда он поступил в четвертый класс гимназии. В возрасте 16 лет Пик сдал выпускные экзамены и был принят в Венский университет. В следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году он защитил докторскую диссертацию, а в 1881 году был назначен ассистентом на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, а в 1892 году — пэр-профессором (полным профессором). Университет в Германии.
Спектр математических интересов Пика был очень широк. В частности, он написал статьи по функциональному анализу и дифференциальной геометрии, эллиптическим и авериевым функциям, теории дифференциальных уравнений и комплексному анализу, в общей сложности более 50 проблем. Его имя связано с Пиком Пика, Пиком Неванлинны Помехи и Пиком Шварца.
Теорема Пика для вычисления площади многоугольника, открытая в 1899 году, широко известна. Некоторое время теорема оставалась незамеченной, но в 1949 году польский математик Хуго Штейнгауз включил теорему в свой знаменитый «Калейдоскоп математики». С тех пор теорема Пика стала широко известна.
Теорема привлекла большое внимание, и люди стали восхищаться ее простотой и элегантностью.
В Германии эта теорема включена в школьные учебники.
Когда 12 марта 1938 года нацисты вошли в Австрию, он вернулся в Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в Терезиенштадт, лагерь, созданный нацистами на севере Чехии, где он умер через две недели в возрасте 82 лет.
C-число узлов сетки, расположенных в пределах полигона,
D-число узлов сетки, расположенных на границе полигона.
Основным требованием для применения формулы Пика является то, что многоугольник, изображенный на клетчатой бумаге (сетке), должен иметь только целочисленные вершины, то есть они обязательно должны лежать в узлах сетки. (Узел — это пересечение ячеек).
По теме: методические разработки, презентации и конспекты
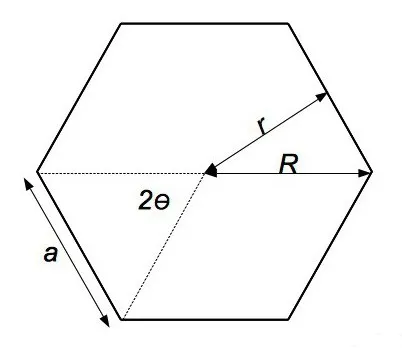
Разработка урока по геометрии для 9 класса «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности».
Разработка плана урока по новому материалу в 9 классе по геометрии «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности» Конспект урока по геометрии.
Площадь прямоугольника. Вычисление площадей фигур на клетчатой бумаге с помощью формулы Пика
Формирование понятия «площадь» как величины; единицы площади — проверка формул площади прямоугольника и квадрата — способы вычисления площади треугольников и других многоугольников, используя.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Данная презентация посвящена выведению различных формул, показывающих связь между стороной правильного многоугольника и радиусом периметра окружности. В презентации также рассматриваются дополнительные формулы.
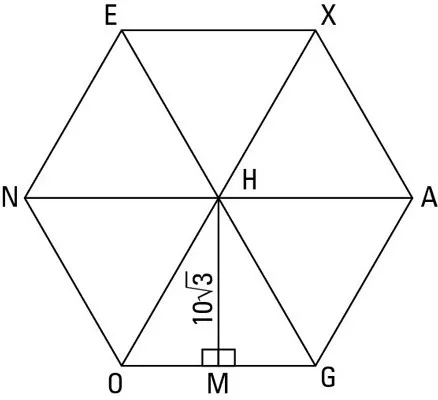
Урок по теме «Вычисление площадей фигур на клетчатой бумаге. Формула Пика».
Разработка урока геометрии по теме «Вычисление площадей фигур на клетчатой бумаге». Формула Пика» 8 класс. Включает конспект и презентацию. Вы можете использовать его для подготовки к ГИА и ЕГЭ по математике.
Площадь многоугольника. Формула Пика. Реферат-исследовательская работа.
Объект исследования. Метод исследования: «Грант. Можно предположить, что существует несколько способов найти многоугольники многоугольников на клетчатой бумаге с помощью c.

Методическая разработка по теме «Решение задач на вычисление площадей многоугольников».
Цель урока: закрепить знания формул для вычисления площади многоугольников.
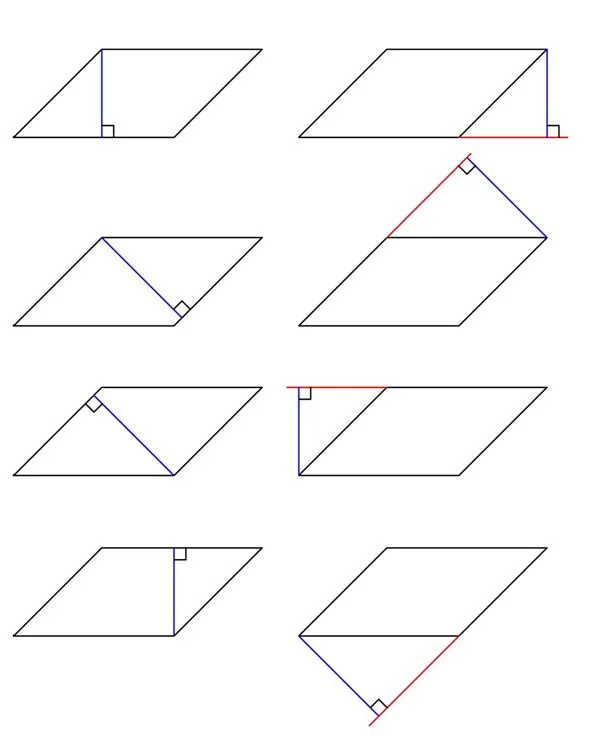
Вычисление площади многоугольника
Тема: Площадь многоугольника.Цель урока: Создать условия для расширения представлений о вычислении площади геометрических фигур, познакомить с формулой Пика и ее применением.








