Наименьшее общее кратное: как найти. Как найти общее кратное

Между единицей и делителем существует определенная связь. Действительно, если A кратно B, то B является делителем этого числа, и наоборот.

НОД и НОК

Мы продолжаем изучать разделения. В этом уроке мы рассмотрим такие понятия, как NOD и NOC.

NOD — наибольший общий делитель.

НОК — наименее распространенное множественное число.

Это довольно скучная тема, но ее необходимо понять. Не понимая этого, вы не сможете эффективно работать с дробями, что является настоящим недостатком в математике.

Наибольший общий делитель

Значение. Наибольший общий делитель A и B — это наибольшее число, которое A и B делят без остатка.

Чтобы получить представление об этом определении, замените A и B двумя числами. Например, замените A на число 12, а B на число 9. Затем прочитайте это определение.

Наибольший общий делитель чисел 12 и 9 — это наибольшее число, на которое делятся числа 12 и 9.

Из определения ясно, что речь идет об общем делителе 12 и 9. Делитель является наибольшим из всех существующих делителей. Нам нужно найти этот наибольший общий делитель (НОД).

Существует три способа найти самую большую аудиторию для двух номеров. Первый метод требует много времени, но дает хорошее понимание предмета и ощущение его смысла.

Второй и третий методы очень просты и быстро находят узелок. Рассмотрите все три метода. Вы сами решаете, какой из них использовать.

Первый метод заключается в том, чтобы найти все возможные деления на два числа и выбрать наибольшее деление. Рассмотрим этот метод для следующего примера: найти наибольший общий делитель 12 и 9.

Сначала найдите все потенциальные делители числа 12. Для этого разделите 12 от 1 до 12 со всеми делителями. Если делитель может делиться на 12 без остатка, выделите его синим цветом и заключите в скобки с соответствующим объяснением.

12:1 = 12 (12 делится на 1 без остатка, поэтому 1 является делителем 12)

12:2 = 6 (12 делится на 2 без остатка, поэтому 2 является делителем 12)

12 : 3 = 4 (12 делится на 3 без остатка, поэтому 3 является делителем 12)

12 : 4 = 3 (12 делится на 4 без остатка, поэтому 4 является делителем 12)

12: 5 = 2 (2 с остатком) (5 не является делителем 12, потому что 12 не делится на 5 без остатка)

12: 6 = 2 (6 является делителем 12, так как 12 делится на 6 без остатка).

12:7 = 1 (5 с остатком) (7 не является делителем 12, так как 12 не делится на 7 без остатка).

12:8 = 1 (с балансом) (8 не является делителем 12, потому что 12 не делится на 8 без баланса).

12: 9 = 1 (3 с остатком) (9 не является делителем 12, так как 12 не делится на 9 без остатка).

12: 10 = 1 (2 с остатком) (10 не является делителем 12, так как 12 не делится на 10 без остатка).

12: 11 = 1 (1 с остатком) (11 не является делителем 12, так как 12 не делится на 11 без остатка).

12: 12 = 1 (12 является делителем 12, так как 12 делится на 12 без остатка).

Теперь найдите делитель числа 9. Для этого проверьте все делители от 1 до 9.

9:1 = 9 (1 является делителем 9, так как 9 делится на 1 без остатка)

9: 2 = 4 (1 имеет остаток) (2 не является делителем 9, так как 9 не делится на 2 без остатка)

9 : 3 = 3 (3 является делителем 9, потому что 9 делится на 3 без остатка)

9 : 4 = 2 (1 на остаток) (4 не является делителем 9, так как 9 не делится на 4 без остатка)

9 : 5 = 1 (4 — остаток) (9 не делится на 5 без остатка, поэтому 5 не является делителем 9)

Второй способ нахождения НОД

Теперь рассмотрим второй метод нахождения наибольшего общего делителя. Суть этого метода заключается в анализе обоих простых чисел и умножении их на общее число.

Пример 1. Найдите НОД 24 и 18.

Сначала проанализируйте оба числа в простых множителях.

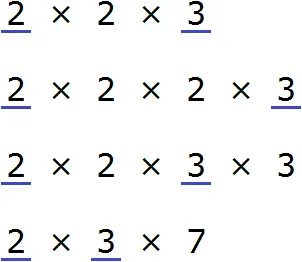
Затем умножьте их на общий множитель. Чтобы избежать путаницы, можно подчеркнуть общий множитель.

Рассмотрим разложение числа 24. Его первый коэффициент равен 2. Найдите тот же коэффициент в разложении 18 и проверьте, что он там тоже присутствует. Подчеркните оба парных слова.

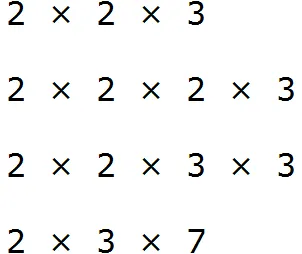
Давайте снова посмотрим на 24 разложения: второй фактор также равен 2. Найдите тот же фактор в 18 разложениях и проверьте, что его нет во втором. Тогда мы ничего не подчеркиваем.

Следующие две из 24 разработок также отсутствуют в 18 разработках.

Перейдите к последнему множителю в разработке 24. Мы ищем тот же коэффициент в расширении 18 и видим, что он там тоже присутствует. Мы подчеркиваем оба треугольника.

Таким образом, общими множителями для 24 и 18 являются множители 2 и 3. Эти множители необходимо перемножить, чтобы получить НОД.

Давайте снова посмотрим на 24 разложения: второй фактор также равен 2. Найдите тот же фактор в 18 разложениях и проверьте, что его нет во втором. Тогда мы ничего не подчеркиваем.

Вычисление НОК, правила в математике

Существуют различные правила и алгоритмы для нахождения математических ноксов. Самый простой способ — рассчитать НОК двух номеров участия. Этот метод прост, но приемлем для небольших натуральных чисел.

Необходимо создать серию чисел, кратных каждому выбранному значению.

Из рядов видно, что числа 12 и 24 появляются в обоих рядах. Это обычные кратные числа. Однако 12 — это меньшее число.

Как найти НОК через НОД

NOC можно определить с помощью NOD (большего общего делителя).

В этом разделе есть несколько понятий, которые требуют разъяснения.

Первое число — это натуральное число, которое может делиться само на себя или только на единицу.

Наименьшее простое число — 2. Это единственное натуральное простое число. Все остальные — нечетные числа.

Множество чисел делится не только на себя и единицу, но и на другие целые положительные числа.

Эти числа являются делителями 8 и 36 (делители). Это те, кто может разделить 8 и 36 без остатка. В обоих приведенных выше примерах делители (8 и 36) являются комплексными числами, поскольку имеют более трех делителей.

Приведенные выше серии имеют одинаковые делители. 1, 2, 4 и 8.

Самое большое число — 8. Это наибольший общий делитель.

Наибольший общий делитель (НОД) — это число, в котором выбранная пара (или более) чисел не делится на остаток.

Существуют пары чисел, которые имеют только один общий делитель. Затем они сначала вызываются друг против друга: НОД (9, 8) = 1, НОД (12, 10) = 1.

В следующем примере показана пара чисел со значениями NOD и NOC.

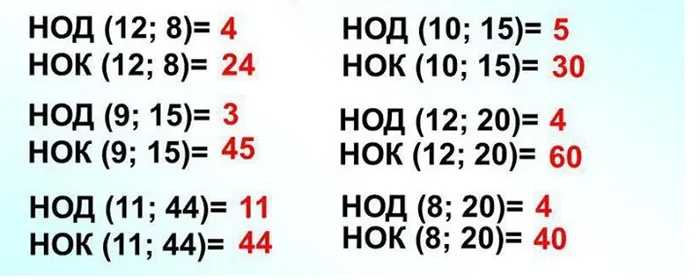
Решением проблемы нахождения NO из NOD является следующее уравнение.

НОК от a и b равен произведению a и b на наибольший общий делитель a и b (НОД(a, b)).

Этот вывод показывает, что НОК и НОД взаимосвязаны. Наименьшее общее кратное можно легко найти в наибольшем общем делителе двух или более натуральных чисел.

Как найти НОК через разложение чисел

Помимо генерации серии умножений для каждого из двух выбранных натуральных чисел, для определения правильного НОК используется метод мультипликативного разложения.

Найденный первый элемент первой разработки перед умножением сравнивается с элементом второй разработки.

После разложения 9 на простые множители появляется ряд элементов.

После разложения на 12 появляется последовательность.

После факторизации числа 9 получается 3*3. После факторизации 12, получаем: 2 * 2 * 3. Объединение обоих множителей дает произведение: 3 * 3 * 2 * 2 * 2 = 36.

Наименьшее общее кратное 9 и 12 равно 36.

Чтобы проверить, давайте запустим действие.

На практике мы пишем NOC (9, 12) = 36.

Такая операция может быть использована для нахождения более сложных чисел NOK.

Число 50 делится на 1, 2, 5, 10, 25 и 50.

Число 180 делится на 1, 5, 15, 30, 45, 90 и 180.

Анализ 50 на кратные числа дает 2, 5, 5.

Разложите 180 на 2, 2, 3, 3, 3, 5.

Из первой разработки получаем 2*5*5. Сравнение со второй разработкой дает 2 и 23. При умножении этого ряда получается произведение 2 * 5 * 5 * 2 * 3 * 3 = 900. Это наименьшее общее кратное 50 и 180.

Следовательно, NOC (50, 180) = 900.

Существует еще один простой способ найти EAP. Он подходит, когда одно число делится на другое поровну. Например, НОК (15, 30) = 30, НОК (20, 80) = 80, НОК (16, 48) = 48.

Если два числа не имеют общего делителя, их можно просто перемножить, чтобы получить NOQ. Например, НОК (7, 8) = 56, НОК (4, 9) = 36, НОК (7, 9) = 63.

Число делителей данного значения конечное, а кратных — бесконечное. Природные ценности имеют одинаковую стоимость. Это тот, кто делится с ними без остатка. Разобравшись с понятием самой низкой цены для конкретного экспонента, перейдем к тому, как ее найти.

Частные способы нахождения

Как и в любой математической задаче, существуют особые случаи, когда необходимо найти NEQ. Это помогает в определенных ситуациях.

• если одно из чисел делится на другие без остатка, то самое невысокое кратное этих чисел равно ему (НОК 60 и 15 равно 15);
• взаимно простые числа не имеют общих простых делителей. Их самое небольшое значение равно произведению этих чисел. Таким образом, для чисел 7 и 8 таковым будет 56;
• это же правило работает и для остальных случаев, включая специальные, о которых можно прочитать в специализированной литературе. Сюда же следует отнести и случаи разложения составных чисел, которые являются темой отдельных статей и даже кандидатских диссертаций.

Особые случаи встречаются реже, чем стандартные примеры. Однако они позволяют научиться работать с деталями разной степени сложности. Это особенно верно для дробей с неравными знаменателями.

Немного примеров

Давайте рассмотрим несколько примеров, которые помогут вам понять, как найти наименьшее общее кратное.

1. Находим НОК (35; 40). Раскладываем сначала 35 = 5*7, затем 40 = 5*8. Добавляем к наименьшему цифру 8 и получаем НОК 280.
2. НОК (45; 54). Раскладываем каждое из них: 45 = 3*3*5 и 54 = 3*3*6. Добавляем к 45 цифру 6. Получаем НОК, равный 270.
3. Ну и последний пример. Есть 5 и 4. Простых кратных для них не имеется, поэтому наименьшее общее кратное в этом случае будет их произведение, равное 20.

Примеры позволят вам понять NOC, нюансы и как найти смысл этих операций.

Найти EAE гораздо проще, чем кажется на первый взгляд. Используются как простые разложения, так и простые умножения значений между ними. Это умение работать с математическим отделом полезно для дальнейшего изучения математических предметов, особенно дробей различной сложности.

Не забывайте регулярно решать примеры, используя различные методы. Это развивает логику и помогает запомнить многие термины. Если вы научитесь находить такие экспоненты, вы сможете успешно работать с другими разделами математики. Успехов вам в изучении математики!

Таким образом, произведение простого множителя наибольшего числа и простого множителя второго числа, которое не входит в развитие наибольшего числа, является наименьшим общим кратным.

Определение наименьшего общего кратного

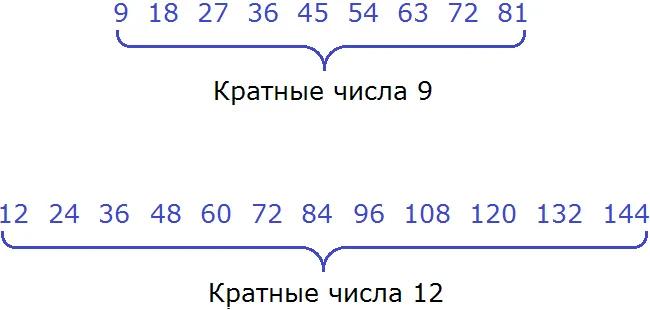
Число b кратно a, если b делится на a без остатка. Это произносится как «b кратно a». Он обозначается k.

кратные числа 3 или К(3) : 6, 9, 12,15, 18 и т.д.

Может существовать бесконечное количество кратных чисел.

Общее кратное двух положительных целых чисел — это число, которое одинаково делится на оба.

Наименьшее общее кратное двух натуральных чисел — это наименьшее общее кратное этих чисел. Они называются НОК.

Например, НОК (5, 9) — это наиболее часто встречающееся кратное 5 и 9.

Нахождение НОК

Чтобы найти наименьшее общественное кратное, можно использовать один из двух методов

Для двух/небольших чисел

Если речь идет о двух числах (или небольшом числе), процесс нахождения НОК выглядит следующим образом

1. Записываем в ряд кратные для каждого числа по возрастанию.
2. Находим первое совпадение в полученных рядах чисел. Это и есть НОК.

Найдите минимальное общественное кратное примеров чисел 6 и 14.

6: Кратные решения, такие как 12, 18, 24, 30, 36, 42, 48 и т.д. 14: кратные 28, 42, 56 и т.д.

Таким образом, НОК (6, 14) = 42.

Для нескольких/больших чисел

Этот метод подходит при работе с большими числами или когда необходимо найти НОК, содержащие более трех чисел.

Сперва раскладываем числа на простые множители – простые числа, которые делят число нацело (их количество для разных чисел, также, может быть разным). Для удобства начинаем с самого маленького значения и заканчиваем самым большим.

Например, найдем его НОК (12, 28, 32).

Решение Разложите эти числа на их первые коэффициенты.

Среди факторов нескольких факторов (12), цифра 3 не присутствует в большинстве (32) — среди агентов медианного числа (28), цифра 7 не присутствует.

Таким образом, НОК (12, 28, 32) = 32⋅3⋅7 = 672.

Иные случаи

1. если одно из чисел, требующих минимального общего множества общих чисел, является целым числом деления с другими числами, то это число — NOK.

Например, НОК (20, 40, 80) = 80.

2. слагаемое первого числа является произведением этих чисел, так как нет общего первого множителя.

Наименьшее открытое кратное или LSN от A и B — это наименьшее число, которое можно разделить одновременно на A и B. Другими словами, она кратна A и B.

Как найти наименьшее общее кратное чисел

Студенты часто встречают такую формулировку в математических работах: «найдите наименьшее общее кратное числа». Это то, что вам нужно научиться делать, если вы хотите выполнять различные действия с дробями с разными знаменателями.

Нахождение наименьшего общего кратного: основные понятия

Чтобы понять, как рассчитать NOC, необходимо сначала определить значение термина «множественность».

Кратное A — это натуральное число, деленное на неравное. Таким образом, 15, 20, 25 и т.д. Их можно считать более множественными, чем 5.

В то время как делители числа могут быть ограничены, кратные числа бесконечны.

Общие кратные натуральных чисел — это числа, которые делятся без остатка.

Как найти наименьшее общее кратное чисел

Наименьшее общее кратное (НОМК) числа (двух, трех или более) — это наименьшее физическое число, деленное на все эти числа без остатка.

Существует несколько способов найти НОК.

Для небольших чисел удобно записывать все кратные им числа на одной строке, пока не будет найдено общее. Множественное число пишется с прописной буквы К.

Например, кратное 4 можно записать как

Таким образом, мы видим, что наименьшая аудитория для 4 и 6 равна 24. Этот символизм заключается в следующем.

Если числа большие, или если вам нужно найти наименьшее общественное кратное трех или более чисел, предпочтительнее использовать другой метод вычисления NOK.

Для выполнения задания необходимо проанализировать предложенные числа в первом факторе.

Сначала напишите анализ большего числа, а затем запишите его под анализом других чисел.

Каждое числовое деление может содержать разное количество множителей.

Например, проанализируйте 50 и 20 в первом факторе.

При расширении меньшего числа следует выделить множитель, отсутствующий в первом расширении большего числа, и добавить его. В приведенном примере не хватает двух.

Теперь мы можем вычислить наименьшие общественные кратные 20 и 50.

(20, 50) = 2 * 5 * 5 * 2 = 100

Таким образом, произведение простого множителя наибольшего числа и простого множителя второго числа, которое не входит в развитие наибольшего числа, является наименьшим общим кратным.

Чтобы найти три и более числовых коня, как и в предыдущем случае, необходимо проанализировать их все в первом факторе.

Например, найдите наименьшие представления 16, 24 и 36.

Поэтому факторизация больших чисел не включает только два колеса два (в 24-часовом развитии есть одно).

Поэтому их необходимо добавить к расширению большего числа.

(12, 16, 36) = 2 * 2 * 3 * 3 * 3 * 2 * 2 = 9

Существуют особые случаи, когда необходимо определить наименьшее общее кратное. Например, если одно число можно разделить на другое число и еще на одно число, то максимальное из этих чисел не является самым распространенным.

Например, 12 и 20 НОК равны 20.

Если вам нужно найти наименьшую аудиторию для первого числа, у которого нет такого делителя, то мок равен произведению.