Он может быть рассчитан по одному из двух типов. Оба предоставляют правильные и точные данные. Последний вариант полезен, когда базовая область уже известна. Если неизвестно, то проще одновременно умножать три линейных измерения, избавляясь от ненужных процессов.
По какой формуле вычисляется объем прямоугольного параллелепипеда?
Параллельный лепсид — это многогранник, состоящий из шести четырехугольных поверхностей с параллельными гранями на пару. Существуют различные виды параллельных видов, в зависимости от типа четырехугольника, на котором они основаны. Давайте рассмотрим, что это такое и чем они отличаются. Узнайте, как найти площадь и сумму подобий прямоугольников и наклонных, используя известные типы.
Куб или прямоугольник — это шестиугольный многогранник с прямоугольником в основании. Его противоположные поверхности взаимно параллельны, а верхнее схождение перпендикулярно. Ребра, выведенные из одной вершины, называются размерами.
Геометрические свойства тела:.
- Диагонали многогранника в месте пересечения делятся на равные отрезки.
- Место пересечения диагоналей – центр симметрии геометрического тела.
- Размеры противоположных граней равны.
- Квадрат диагонали равен сумме квадратов измерений.
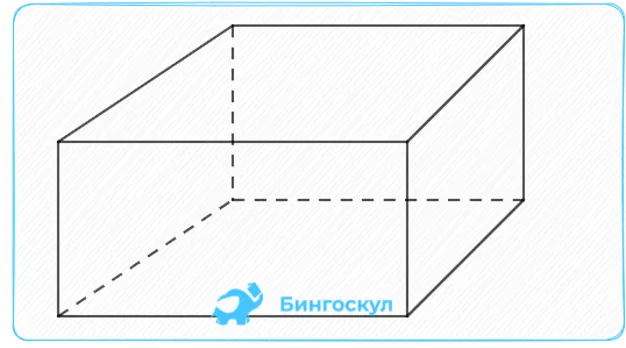
Рассмотрим объем прямоугольной параллели и ее площадь.
Как найти площадь параллелепипеда
Площадь — это числовая характеристика плоской фигуры, обозначающая количество квадратов на ее стороне, равное одному вписанному на ее поверхности. Она рассчитывается как сумма площадей шести прямоугольных поверхностей.
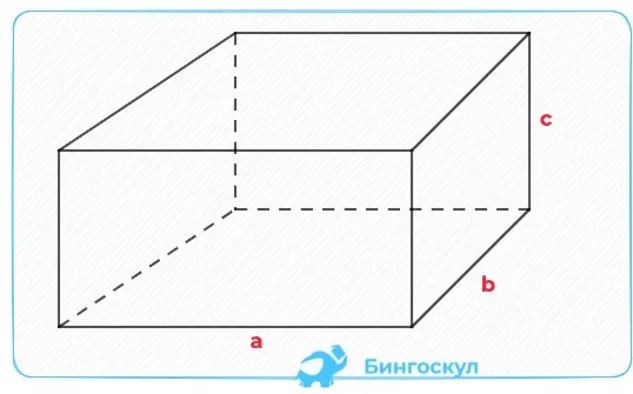
Расположение: AB, BC и AC — площади поверхности.
По мере объединения сторон в пары, полученная сумма умножается на два.
Например, есть габаритное тело.
Общая площадь выглядит следующим образом.
S = 2 * (3 * 4 + 4 * 5 + 5 * 3) = 2 * (12 + 20 +15) = 2 * (47) = 94 см.
Объем параллелепипеда
Объем — это числовая характеристика тела, отражающая занимаемое им пространство. Он определяется как количество кубов со сторонами, которые помещаются в многоугольник.
Объем прямоугольной параллели вычисляется по типу: v = a * b * c, где
a, b и c — размеры полиэдра, измеренные от одной точки, или длина, ширина и высота.
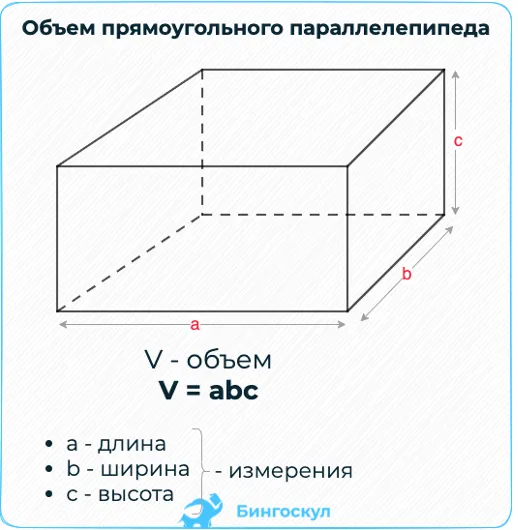
Чтобы найти объем прямоугольной прямой по заданному типу, замените в нем размеры поверхности многоугольника.
Измеряется в кубических единицах, например, сантиметрах, метрах или литры: один литр равен одному кубическому метру одного разряда.
Физический смысл объема прост: кубический метр равен одному кубическому метру.
- по высоте в параллелепипед поместится 4 куба с гранью 1 см;
- по ширине – 3 штук;
- по длине – 5 кубиков.
Если входные данные имеют площадь одной поверхности, требуется второй тип (sосновной (с) и длина третьей грани (h) или высота.
Смысл расчета остается прежним — умножьте поверхность на длину третьей стороны тела.
Объем наклонного параллелепипеда
Наклонные параллели — это четырехугольные призмы с прямоугольником в основании, стороны которого образуют угол 90°.
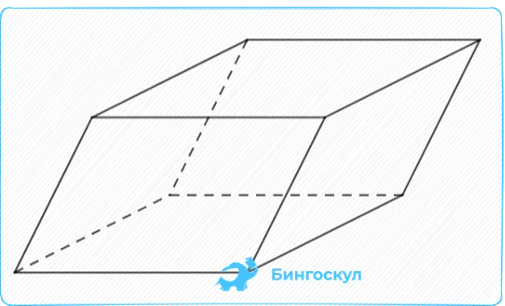
Площадь и объем наклонной параллельной вершины вычисляется по тому же типу, что и прямоугольника: v = sосновной (с * H или v = a * b * c.
Площадь рассчитывается по-другому, но равна сумме боковых граней и поверхности основания.
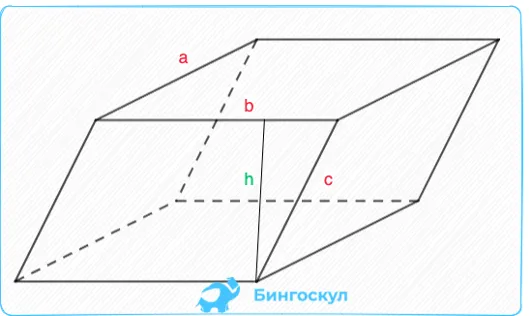
s = s1 + s2 +sосновной (с. Стороны прямоугольника и площадь s1 B s2 Они равны производной ширины по длине прямоугольника, который они представляют: a*c и a*b. Размеры основания, прямоугольника вычисляются следующим образомосновной (с = b * h.
В зависимости от исходных данных был рассмотрен метод нахождения базового сходства для различных типов данных. Для решения более сложных задач необходимо применять другие геометрические и тригонометрические типы для определения необходимых данных.
В 5 классе учащиеся знакомятся с объемной геометрией. Оглянитесь вокруг — мир состоит из параллелей. Поэтому в двусмысленности ищите объем. Узнайте, как это сделать. В статье приведены все виды и правила, которые вам необходимы.
Нахождение объема параллелепипеда: формула и задачи
В данной публикации описано, как находить параллельные объемы и решать комплексные примеры задач.
1. Общая формула
Объемы параллельных уровней равны произведению основания основания на высоту.
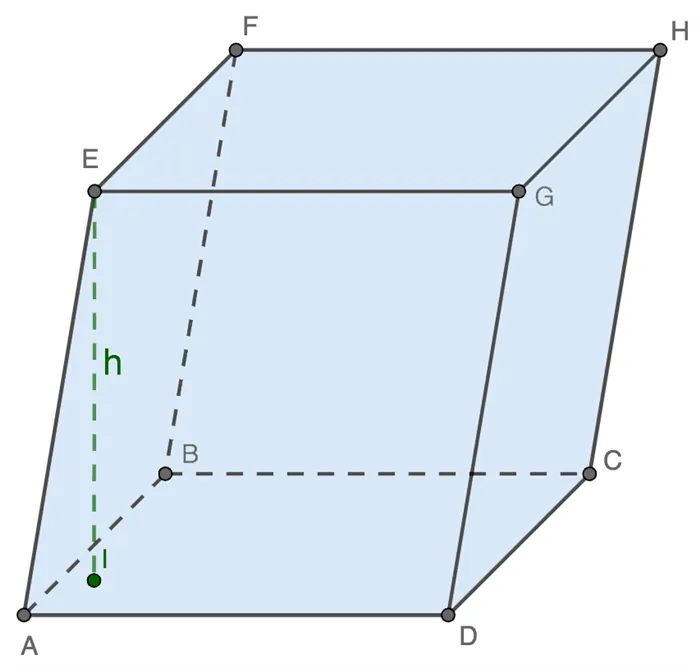
Этот тип применяется ко всем типам геометрических фигур.
- наклонной – боковые грани не перпендикулярны основаниям;
- прямой – все боковые грани (4 шт.) являются прямоугольниками;
- прямоугольной – все грани (боковые и основания) являются прямоугольниками;
- ромбоэдра – все грани являются равными ромбами;
- куба – все грани представляют собой равные квадраты.
2. Объем прямоугольного параллелепипеда
Объем фигуры равен произведению длины ее высоты на ширину.
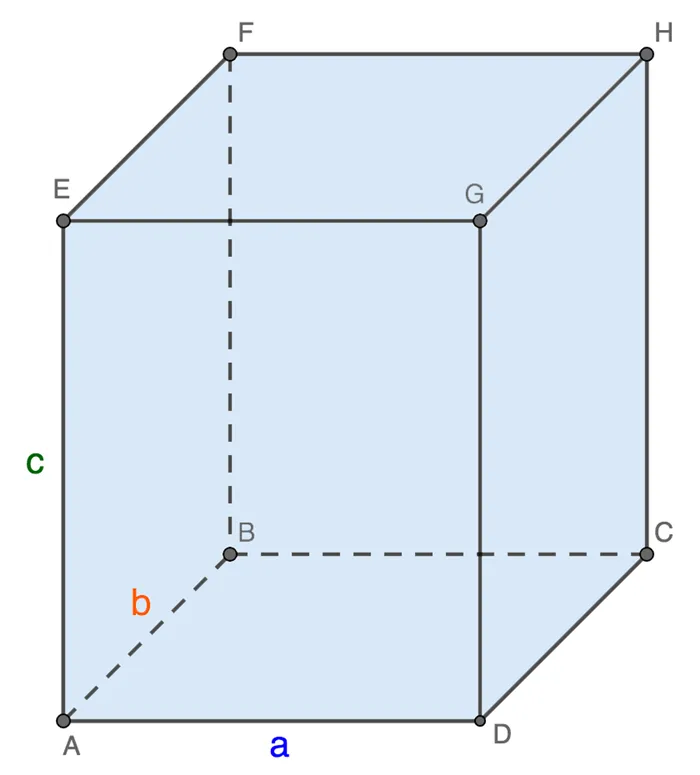
Этот тип вытекает из следующих утверждений
- Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины ( a ) на ширину ( b ).
- Высота фигуры – это длина боковой грани ( c ).
Примеры задач
Работа 1 Если известно, что площадь основания равна 20 см2, а высота 7 см, то найдем объем параллели.
Решение: поменяйте местами известные нам значения и используйте первый тип: v = 20 см2⋅7 см = 140 см 3.
Задача 2 Дана прямоугольная расщелина с параллельными прямыми. Длина и ширина основания равны 9 см и 5 см соответственно, а его высота — 6 см. Найдите объем фигуры.
Используйте формулу для этого положения: v = 9 см ⋅ 5 см ⋅ 6 см = 270 см3.
Вы можете использовать электронный калькулятор, если вы обучены решению задач и можете вычислить объем параллельного пира с закрытыми глазами. Давайте рассмотрим несколько примеров.
Формула расчета в двух вариантах
Таким образом, для расчета типа нам необходимо знать длину, ширину и высоту измеряемого объекта. Эти данные должны быть охарактеризованы как A, B и C соответственно, в то время как опухоли обычно представляются буквой V. Для определения объема подобия прямоугольника в этом случае используется вид: V = a x b x c.
Чтобы определить объем бассейна, необходимо перемножить его длину, ширину и глубину. Чтобы было проще понять, давайте на примере разберем правила вычисления объема параллелепипеда. Предположим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется так: 10x3x1,5 = 45 кубических метров, или 45 кубических метров.
Может появиться еще один человек с отличием. Это произведение площади основания высоты. Виды: v = s x h. Это высота параллели. S — площадь основания, выраженная как произведение двух сторон основания. Обычно они обозначаются как a и b: s = a x b.
Он может быть рассчитан по одному из двух типов. Оба предоставляют правильные и точные данные. Последний вариант полезен, когда базовая область уже известна. Если неизвестно, то проще одновременно умножать три линейных измерения, избавляясь от ненужных процессов.
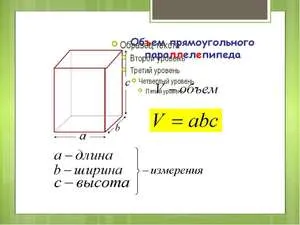
О чем еще следует знать для правильности расчета?
Чтобы вычислить объем параллели, нужно понять, какой она формы. Это призма, основанием которой является прямоугольная призма. Параллельный лель имеет шесть поверхностей, каждая из которых прямоугольная. Существует несколько типов элементов. Особых различий в принципах расчета нет, но сами цифры отличаются по внешнему виду. Таким образом, можно выделить следующие типы
- Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
- Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
- Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.
Также важно помнить, что при выполнении расчета каждый компонент типа должен иметь одинаковые размеры. Пренебрежение этим простым правилом приведет к неправильным результатам. Единственная проблема с простым подсчетом уроков математики заключается в том, что они неадекватно оцениваются. Если вы планируете свои расчеты и допускаете ошибки, проблема может оказаться более серьезной.
Не следует думать, что основные формулы для определения объема геометрической фигуры можно найти только на уроках математики. В большинстве случаев они оказываются полезными на более поздних этапах жизни. В частности, во время ремонтно-строительных работ, при оформлении интерьера и декорировании и во многих других случаях. Затем необходимо подобрать правильную формулу.
В целом, объем параллелепипеда равен произведению трех линейных размеров: длины, ширины и высоты. Параметры напрямую зависят от трех единиц измерения для каждого вращения и оборота. Результаты не меняются.
Вы можете использовать электронный калькулятор, если вы обучены решению задач и можете вычислить объем параллельного пира с закрытыми глазами. Давайте рассмотрим несколько примеров.
Объем параллелепипеда
Найти объем параллелограмма очень просто. Для этого необходимо знать длину и высоту трех или двух сторон. Чтобы облегчить вычисление объема параллелограмма, были созданы два компьютера для разных исходных данных. Просто введите известные значения и получите результаты в режиме онлайн.
Параллелограмм — это многогранник, состоящий из шести граней, все из которых являются параллелограммами.
Прямоугольник — это параллелограмм, все стороны которого прямоугольные.
Объем параллелепипеда через стороны и высоту
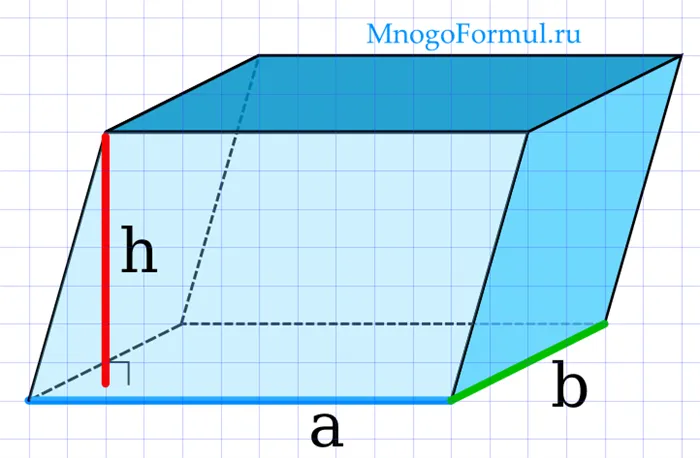
Формула для нахождения объема параллелограмма по его высоте и сторонам:.
Поскольку внизу параллелограмма находится прямоугольник, формула ab — это площадь прямоугольника внизу параллелограмма. Формула может быть сокращена следующим образом
Используя эту формулу, можно найти и прямоугольник, и наклонный параллелограмм.
Пример расчета
Найдите объемы параллелограммов со сторонами 3 см, 4 см и 5 см. Подставьте эти значения в первое уравнение и выполните расчет: площадь параллелограмма — это площадь параллелограмма.
Площадь — это числовая характеристика плоской фигуры, обозначающая количество квадратов на ее стороне, равное одному вписанному на ее поверхности. Она рассчитывается как сумма площадей шести прямоугольных поверхностей.
Объем прямоугольного параллелепипеда
На уроках математики в пятом классе школы ученики знакомятся с темой прямоугольников. Это один из первых элементов серии с томами. Величины и формулы для их нахождения — это те, которые обсуждались сегодня.
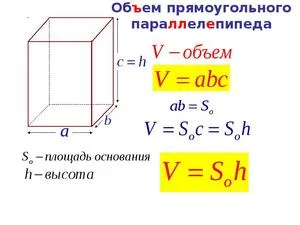
Определения
Прямоугольное тело — это фигура, все поверхности которой прямоугольные. У него шесть сторон. Поверхности пересекаются друг с другом, образуя ребра, а их 12.
У прямоугольника четыре стороны и два дна. В нашей жизни мы часто сталкиваемся с этой формой: шкафы, холодильники, коробки — все они имеют форму прямоугольного параллелепипеда.
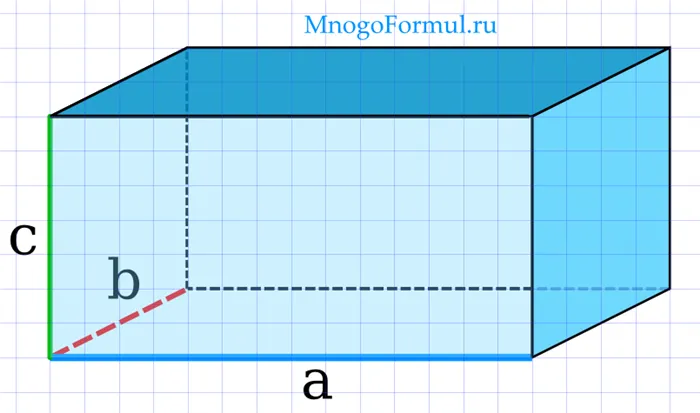
Рисунок 1.Прямоугольный параллелепипед
Формула объема данной фигуры
Объем куба с длиной стороны в одну единицу (фигура, у которой все стороны квадратные) называется единицей объема.
Если мы добавим такой куб к дну (рис. 3), то нам понадобится четыре кубических единицы в длину и три кубических единицы в ширину.
Рисунок 3.Прямоугольники, заполненные кубическими сферами
Таким образом, для заполнения базы нам необходимо
3 x 4=12 — так вычисляется площадь.
Чтобы заполнить всю форму и узнать объем, нужно подсчитать, сколько слоев кубиков помещается в высоту. Например, если 2, то объем будет равен
Поэтому, учитывая, что длина основания фигуры равна 4 единицам, ширина — 3, а высота — 2, нужно найти произведение этих величин или измерений, чтобы вычесть объем прямоугольного параллелограмма. Трехмерная форма называется трехмерным или объемным измерением.
Для обозначения объема используется буква V.
Типы прямоугольных параллельных объемов следующие: — Прямоугольный параллельный объем (R), Прямоугольный параллельный объем (R), Прямоугольный параллельный объем (R), Прямоугольный параллельный объем (R).
При необходимости все рабочие данные должны быть переведены в единицы измерения.
Единицами измерения являются $ мм^3, см^3, дм^$ 3 и т.д. Важно правильно читать: 400 м^$ 3 или кубических метров и т.д.
Британский жонглер провел 44 дня в стеклянной прямоугольной параллельной леле, парящей над Темзой. В его распоряжении были только вода, подушки, матрасы и письменные принадлежности.
Работа:. Вычислите объем фигуры шириной 4 дм, длиной 50 мм и высотой 10 см.
Решение. Во-первых, все данные должны быть переведены в единицы измерения.
Таким образом, $ v = 200 см^$ 3 объема.
Используя специальную единицу измерения, измерьте объем жидкости — литр (1 л).
Древние измерения жидкостей, например, кор = 220 литров, бат = 22 литра.
Измерение объема:.
$ 1 м^3 = 1 000 дм^3 = 1 000 000 см^3 $
Таким образом, для расчета типа нам необходимо знать длину, ширину и высоту измеряемого объекта. Эти данные должны быть охарактеризованы как A, B и C соответственно, в то время как опухоли обычно представляются буквой V. Для определения объема подобия прямоугольника в этом случае используется вид: V = a x b x c.
Объем прямоугольного параллелепипеда
ParallelePipe — это шестисторонний многогранник, каждая сторона которого представляет собой прямоугольник.
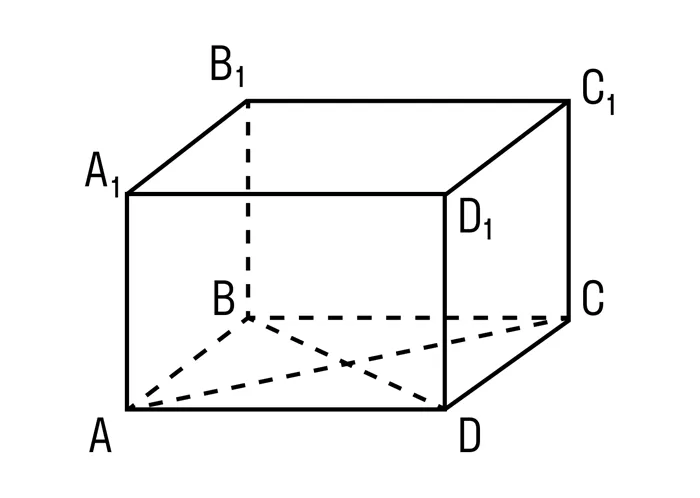
Прямоугольный прямоугольник — это параллелепипед, у которого все поверхности являются прямоугольниками.
Виды объемов прямоугольных параллелей
Чтобы вычислить объем прямоугольной параллели, найдите произведение ее длины, ширины и высоты.
Чтобы не запутаться в типах, запомните таблицу контрактов.
Боковая площадь
Общая поверхность
ПРИМЕР 1. Каковы объемы параллельных полов 9 см, 6 см и 3 см?
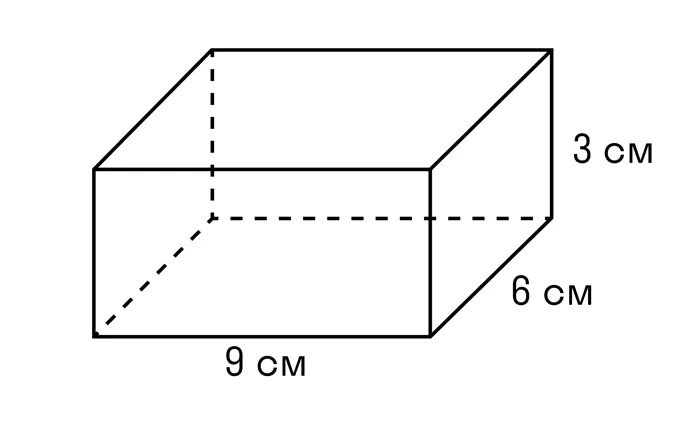
ОТВЕТ: объем прямоугольной параллели равен 162 см3.
Площадь параллели равна произведению площадей основания и высоты.
Эта последовательность указывает на тип параллельной базовой области, которая будет найдена.
Пример 2: Если объем равен 96 см3, а высота 8 см, найдите площадь основания параллельного ключа.
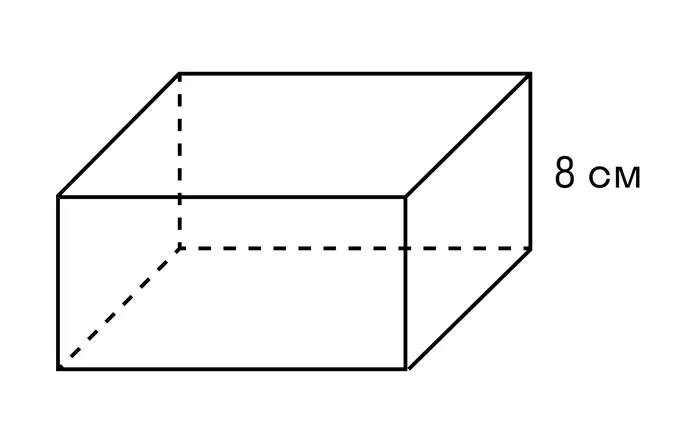
sосновной (с = 82 см3 : 8 см = 12 см2.
ОТВЕТ: площадь основания параллели равна 12 см 2.
Курс математики в Skysmart Web School поможет вам изучить предмет и правильно решить задачу!
Вычисление площади
Как вы уже поняли, вычисление объема параллели может напрямую зависеть от вычисления ее площади. Вычислите количество общих площадей, которые можно найти в параллельных релевантных областях.
Чтобы найти площадь внешней поверхности параллельного пикса, вычислите площадь обеих сторон по отдельности и найдите сумму полученных значений.
Противоположные стороны прямоугольной параллели одинаковы и поэтому принимают вид.
Чтобы вычислить всю поверхность параллели, прибавьте боковые стороны к обоим основаниям основания. Площадь основания прямоугольной параллели одинакова и поэтому получает тип.
Пример 3.Найдем поверхность параллельной пираты, если ее основания имеют длину 6 см и высоту 3 см.
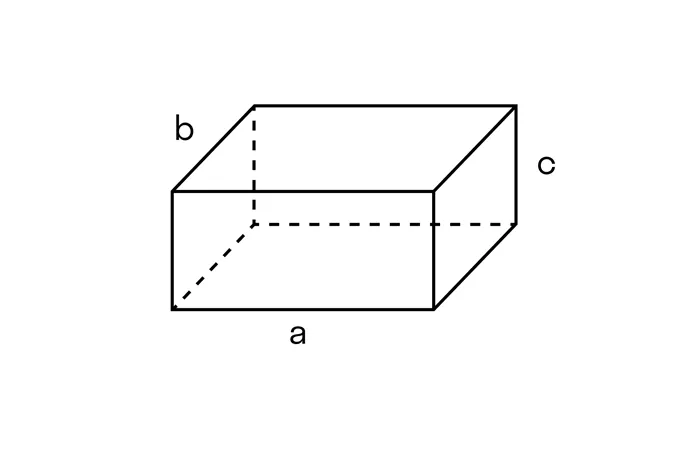
sp. p. = 2 (6 x 4 + 6 x 3 + 4 x 3) = 2 x (24 + 18 + 12) = 2 x 54 = 108 см2.
ОТВЕТ: параллельная поверхность равна 108 см 2.
Как видите, нетрудно вычислить объем и найти площадь параллели.
Задачи на самопроверку
Вы можете использовать электронный калькулятор, если вы обучены решению задач и можете вычислить объем параллельного пира с закрытыми глазами. Давайте рассмотрим несколько примеров.
Задача 1.Найдите объем параллелограмма со сторонами 18 см, 10 см и 7 см.
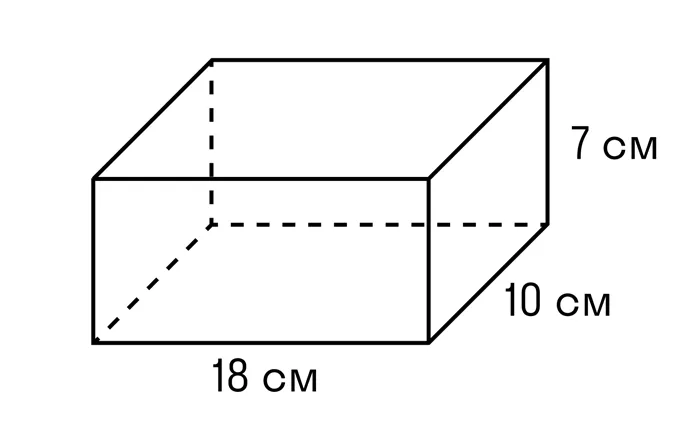
Формула для нахождения объема параллелепипеда:.
ОТВЕТ: объем параллелепипеда равен 1260 см3.
Вопрос 2: Если объем равен 120 см3, а высота 15 см, найдите площадь основания параллелепипеда.
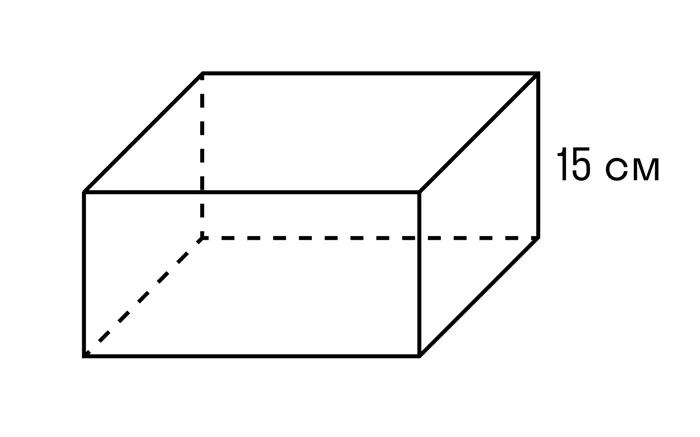
sосновной (с = 120 см3 : 15 см = 8 см2.
ОТВЕТ: площадь основания параллелепипеда равна 8 см2.
Вопрос 3: Если длина основания составляет 30 см, ширина — 12 см, а высота — 5 см, найдите общую площадь прямоугольного тела.
sp. p. = 2 (30 х 12 + 30 х 5 + 12 х 5) = 2 х (360 + 150 + 60) = 2 х 570 = 1140 см2.
ОТВЕТ: общая площадь параллелограмма равна 1140 см2.
Подготовьте все необходимые формулы, когда они вам понадобятся. Сохраните шпаргалку на гаджете или распечатайте ее и сохраните в книге.
Объемы всегда выражаются положительными числами. Это число указывает на точное количество единиц в организме. Например, объем воды в бассейне, сока в графине или почвы на клумбе.
Найти объем прямоугольного параллелепипеда
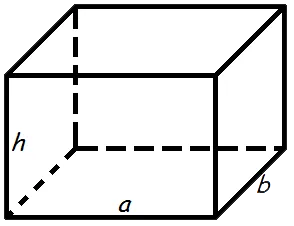Ввод данных.
| a | = |
| b | = |
| h | = |
Ввод данных в калькулятор для вычисления объема прямоугольного параллелепипеда
В электронный калькулятор можно вводить числа и дроби. Подробнее читайте в разделе Правила ввода чисел.
Вы можете использовать значения в тех же единицах в электронном калькуляторе N.B.!
Если у вас возникают проблемы с преобразованием единиц, используйте конвертер единиц для расстояний, конвертер единиц для длин, конвертер единиц для поверхностей и конвертер единиц для объемов.
