Такая форма называется треугольником. Он имеет три углов и такое же количество сторон. Обычно они обозначаются строчными буквами a, b, c или двумя заглавными буквами из названий вершин, образующих начало и конец отрезка. Например, треугольник ABC имеет стороны.
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой многоугольной линией, не имеющей независимых пересечений.

Отрезки полилинии называются ребрами многоугольника и его вершинами являются вершины многоугольника .
Углами многоугольника внутренние углы, образованные соседними сторонами. Количество углов многоугольника равно количеству его вершин и сторон.
Многоугольники называются по числу их сторон. Многоугольник с наименьшим числом сторон называется треугольником; у него только три стороны. Многоугольник с четырьмя сторонами называется четырехугольником, с пятью сторонами — пятиугольником и так далее.
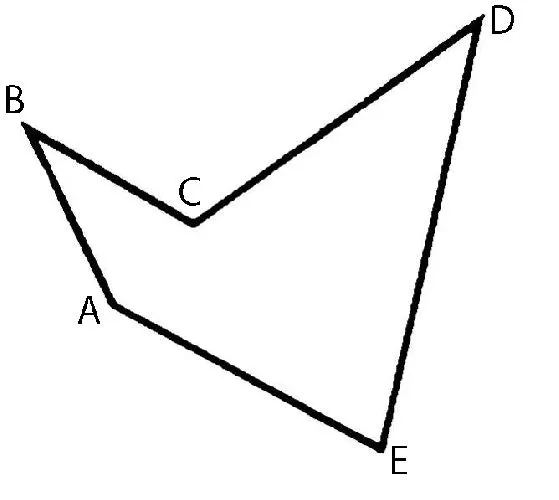
Обозначение многоугольника Он состоит из букв, расположенных по его углам, которые называются по порядку (по часовой или против часовой стрелки). Например, говорится или пишется: Пентагон ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E являются вершинами пятиугольника, а отрезки AB, BC, CD, DE и EA — сторонами пятиугольника.
Периметр
Сумма длин всех сторон многоугольника называется окружностью.
Периметр многоугольника ABCDE равен:
AB + BC + CD + DE + EA .
Если у многоугольника Если все стороны и углы равны, пятиугольник называется правильным. Правильно многоугольника. может быть только выпуклым. многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, которые не имеют общей стороны. Например, отрезок AD — это диагональ :
Единственным многоугольникоm, не имеющий диагонали, является треугольником, потому что он нет углов, не имеет общих сторон.
Если из данной вершины. многоугольника Нарисуйте все возможные диагонали, они будут общими многоугольник на треугольники:
Существует ровно два треугольника, у которых стороны меньше:
t = n — 2,
где t — количество треугольников, а n — количество сторон.
Разделение многоугольника Для треугольников площадь определяется с помощью диагоналей многоугольника, потому что для определения площади любого треугольника многоугольника, это разделить его на треугольники, определить площадь этих треугольников и сложить полученные результаты.
Особое внимание следует уделить правильному определению типов треугольников. Многие теоремы были установлены для одного типа треугольника и не работают для других.
Геометрическая фигура многоугольник
Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой пунктирной линией. Количество соединений в полилинии должно быть не менее трех. Каждая пара отрезков полилинии имеет общую точку и образует углы. Количество углов вместе с количеством сегментов полилинии является основной характеристикой многоугольника. В каждом многоугольнике количество звеньев ограничительной замкнутой полилинии равно количеству углов.
Боковые грани в геометрии — это полилинии, ограничивающие геометрические объекты. Вершины — это пересечения двух смежных сторон, названные в соответствии с их количеством. многоугольники.
Если замкнутая пунктирная линия состоит из трех отрезков, она называется треугольником; четыре отрезка называются четырехугольником, пять отрезков — пятиугольником и так далее.
Треугольник или четырехугольник обозначается заглавными латинскими буквами, указывающими на его вершины. Буквы называются по порядку, по часовой стрелке или против часовой стрелки.
Основные понятия
Описание определения многоугольника, необходимо учитывать некоторые связанные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось, имена многоугольных геометрии основаны на количестве вершин. Если фигура имеет число n, она называется n-угольником:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
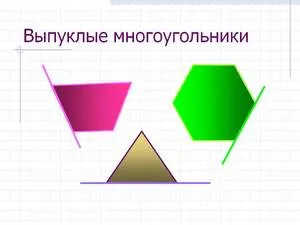
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно разделить на треугольники. Число треугольников на 2 меньше числа сторон.
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. Точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков являются вершинами треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равен 180°.
В зависимости от соотношения сторон друг к другу все треугольники можно разделить на нетреугольники.сколько видов:
- Равносторонние — у которых длина всех отрезков одинаковая.
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
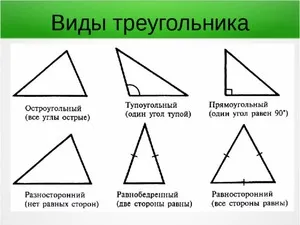
Также принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольник — это плоская фигура с 4 вершинами и 4 отрезками, последовательно соединяющими их.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
Три вершины четырехугольника не могут лежать на одной прямой.
Мы поговорили о многоугольниках. Мы выделили основные типы многоугольникоc и немного рассказать о каждой формуле. Мы уже говорили о том, почему нам необходимо точно знать. вид многоугольника, которые перечислены в постановке задачи.
Треугольник
Треугольник — это не только самый простой многоугольник, Она также является основой для большей части известной геометрии. Все неизвестные плоские фигуры при решении разбиваются на треугольники. Большинство теорем, описывающих точки, отрезки и пропорции, были открыты для этой фигуры. В Америке существует целая энциклопедия треугольников.
В зависимости от элементов треугольника. углов, элементы делятся на:
- Остроугольные.
- Прямоугольны.
- Тупоугольные.
В зависимости от длины стороны треугольники делятся на:
- Произвольные.
- Равнобедренные.
- Равносторонние или правильные.
Особое внимание следует уделить правильному определению типов треугольников. Многие теоремы были установлены для одного типа треугольника и не работают для других.
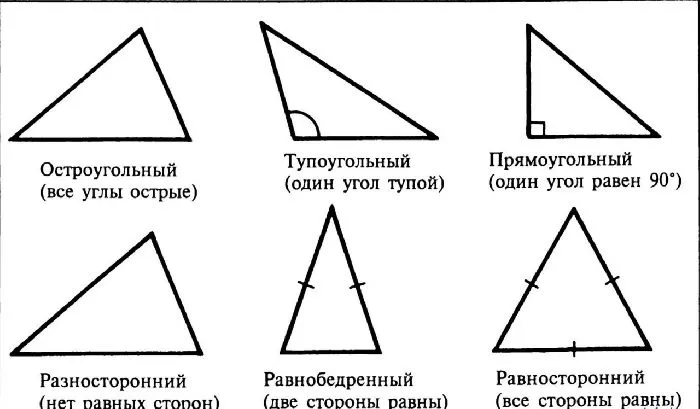
Рисунок 2. Типы треугольников.
Четырехугольник
Четырехугольник имеет столько же вариантов, сколько и треугольник. Однако существует только два основных типа — параллелограмм и трапеция.
Параллелограмм — это выпуклый четырехугольник, стороны которого попарно прямые и параллельные. Обратите внимание, что в определении треугольника никогда не используется параметр «выпуклый», о котором мы говорили в начале. Дело в том, что треугольники всегда выпуклые, а четырехугольники могут быть невыпуклыми.
Параллелограмм, в зависимости от равенства элементов: углов а стороны делятся на следующие фигуры:
- Квадрат.
- Прямоугольник.
- Ромб.
- Произвольный параллелограмм.
Все эти известные нам фигуры являются разновидностями параллелограмма.

Рисунок 3. Типы параллелограммов.
Трапеция — это четырехугольник, две стороны которого параллельны, а две — нет. Однако существует множество четырехугольников, которые не принадлежат ни к одной группе. Такие фигуры называются произвольными четырехугольниками.
Необычные многогранники
Помимо вышеупомянутых форм, существует множество других форм. Количество углов в многоугольнике может быть бесконечным, но найти такие числа можно, только применив правило многоугольника. Это правило используется при добавлении вектора.
Существует отдельное понятие нормального многоугольникоc, т.е. фигуры, у которых все стороны и углы равны. Плоские элементы на гранях объемных объектов образуют многогранники со сложными названиями:
- Тетраэдр.
- Октаэдр.
- Додекаэдр.








