Вместо того чтобы измерять эту неприятную особенность, договорились, что очень полезно, чтобы корень выходил словесно. Старайтесь использовать вьетнамскую теорему как можно чаще.
Квадратные уравнения — 32 примера
Почему важно научиться разбивать квадратные уравнения как орешки?
Потому что решение множества уравнений поможет вам решать квадратные уравнения! И очень жаль, что спотыкаешься о квадраты при решении более сложных уравнений на ЕГЭ, например.
Изучите эту статью и решите все 32 примера вместе с Алексеем, чтобы узнать все о квадратных уравнениях.
От формул дискриминанта до теоремы Вьетнама или как извлечь целый квадрат.
Квадратное уравнение — коротко о главном
Определение.
Квадратичное уравнение — это уравнение вида \(a ^> + bx + c = 0 \) Где ɛ(x \) — неизвестное, ɛ(a \) и ɛ(b \) — коэффициенты квадратного уравнения. уравнение, а ⌘(c \) — свободный член.
Полное квадратное уравнение — это уравнение, в котором коэффициенты ⌘(a \), \(b \) и \(ʔ displaystyle c \) ненулевые.
Уменьшенное квадратное уравнение — это уравнение с коэффициентами\(a = 1 \), т.е. \(^ + bx + c = 0 \).
Неполные квадратные уравнения — это уравнения, коэффициенты\(b \) и/или свободные члены\(c \) которых равны нулю.
Алгоритм решения неполных квадратичных уравнений.
Неполные квадратные уравнения вида \(a ^> + c = 0 \). Где ǫ (ǫ displaystyle a \ ne 0 \) и ǫ (ǫ displaystyle c \ ne 0 \):.
1) Выразим неизвестные: \(^> = \) \(\ displaystyle-\ frac \),.
2) Определите символ \ (\ displaystyle-\ frac \): \ (^> = \) \ (^> = \) \ displaystyle-\ frac \).
Неполные квадратные уравнения вида \(a ^> + bx = 0 \). Где ɛ (ɛ displaystyle a \ ne 0 \), ɛ (ɛ displaystyle b \ ne 0 \):.
(1) Уберите общий множитель \(\ displaystyle x \) из скобок: \(x \ слева (ax + b \ справа) = 0 \), и
(2) Если хотя бы один из множителей равен нулю, то произведение равно нулю. Следовательно, уравнение имеет два корня: \(\ left \ beginx = 0, \ ax + b = 0, \ end
ight.\ Leftrightarrow\ left \ beginx = 0, \ x = -\frac.\ End
ight.\ left \ beginx = 0, \ x = -\frac.\ end
ight. \}
Неполные квадратные уравнения вида \(a ^> = 0 \). Где ǫ(ǫ displaystyle a \ ne 0 \).
В этом уравнении всегда есть только один корень: 모ߡ(x = 0 \).
Алгоритм решения полных квадратных уравнений вида \ (a ^> + bx + c = 0 \). Где ǫ(a, b, c \ ne 0 \)
- если \(D> Дискреционные решения.<-b\pm \sqrt
1) Приведите уравнение к стандартной форме: ǫ(a ^> + bx + c = 0 \), и< \begin_>=\frac>\\_>=\frac>\end \right.\) - если \(D=0\), то уравнение имеет \(1\) корень, который находится по формуле: \(\displaystyle x=\frac\)
- если \(D
2) Вычислите разрешение с помощью следующего уравнения: \(D = ^>-4ac \), которое указывает на количество корней в уравнении: ǫ
0 \), уравнение имеет \(\ displaystyle 2 \) корней, которые можно найти по следующему уравнению: \(D = ^>-4ac \), которое показывает количество корней в уравнении. \ displaystyle x = \ frac<_>> ɑ правая стрелка ɑ левая стрелка ɑ левая стрелка ɑ<_> Решение по теореме Вьетнама<_>Сумма корней квадратного уравнения (вида \(^ + bx + c = 0 \), где \(a = 1 \)) равна \(-b \), а произведение корней равно \(c \), то есть. \ \ \ (ᤩ displaystyle).<_>+
= b \), и \(\ displaystyle
Если квадратное уравнение вида \(a^>+bx+c=0\) имеет корни \(\displaystyle _>,_>\), то его можно записать в виде : \(\displaystyle a\cdot (x-~_>\ cdot
Определение квадратного уравнения
= c \).
Решение методом полных квадратов выглядит следующим образом.
)(x -_>).
Ключевым словом в термине «квадратное уравнение» является слово «квадратичное».
Это означает, что уравнение всегда должно содержать квадрат переменной (x) и не должно содержать x третьего (или более высокого) порядка.
Определение квадратного уравнения выглядит следующим образом.
Как отличать квадратные уравнения от неквадратных
Квадратичное уравнение — это уравнение вида \(a ^> + bx + c = 0 \) Где ɛ(x \) — неизвестное число, ɛ(a \), ɛ(b \) и ɛ(c \). В некоторых числах к числу добавляется ߡ (a \ ne 0 \).
\ (a \) и ʉ (b \) — коэффициенты квадратного уравнения, а ʉ (c \) — свободный член.
Давайте поймем, что перед нами квадратное уравнение, а не другое уравнение.
Уберем знаменатель и умножим каждый член уравнения на \(4x \).
В левой части переместите все члены в порядке убывания x-мощности
Теперь можно с уверенностью сказать, что уравнение квадратное.
С левой и правой стороны перемножьте Ј (8x \).
Это уравнение не является квадратным, хотя в первый раз было ס (^> \)!
Страшно; четвертая и вторая степень … Однако, если мы заменим Ǿ (t =^> \), то получим простое уравнение.
- квадратное
- квадратное
- не квадратное
- не квадратное
- не квадратное
- квадратное
- не квадратное
- квадратное
Два вида квадратных уравнений
\(^> \), но давайте рассмотрим это более подробно. Переместим все влево:.
Как вы знаете, \(^> \) уменьшилось — и теперь является простым линейным уравнением!
Вы можете самостоятельно определить, какое из следующих уравнений является квадратным уравнением.
Все квадратные уравнения можно разделить на два вида.
Полное уравнение — это уравнение, в котором коэффициенты \(a \) и \(b \) и свободный член c ненулевые (как в примере).
Кроме того, между полными уравнениями находятся уравнения сокращенные — это уравнения с коэффициентами\(a = 1 \) (уравнения в первом примере не только полные, но и сокращенные!).
Неполные уравнения — это уравнения, в которых коэффициенты ⌘ (b \) и или свободный член C равны нулю.
Теперь можно с уверенностью сказать, что уравнение квадратное.
Методы решения неполных квадратных уравнений
Почему они придумали такое разделение?
Это разделение связано с методом разрешения. Давайте рассмотрим каждый из них подробнее.
Уравнение вида ax2+bx=0 при отсутствии c
Страшно; четвертая и вторая власть … Однако, если мы заменим ǫ (t =^> \), то обнаружим, что перед нами простое квадратное уравнение.
- Раскладываем выражение как x*(ax+b), равное нулю.
- Так как выражение равно нулю, если хотя бы один из множителей равен ему, то запишем следующую систему уравнений в виде x и ax+b=0.
- Первое решение так и пишется x=0. Второе равенство линейное и решается как равное -b/a.
Научившись решать уравнение в первой степени, вы хотите научиться работать с более сложными уравнениями, такими как квадратное уравнение. Многие знают, как решать типичные квадратные уравнения, но существует особый тип уравнений, называемый квадратным уравнением в краткой форме. Давайте подробнее рассмотрим, как решать неполные квадратные уравнения.
ax2+c=0 при b равном нулю
На сегодняшний день существует три типа таких выражений. В зависимости от этого каждое решение имеет свои свойства, которые зависят от решения конкретной парадигмы, будь то целое или неопределенное число.
Чаще всего это выражается в типе совпадения с квадратными корнями. Как вы решите эту проблему в данном случае? Для этого левую часть необходимо проанализировать на множитель. Алгоритм разрешения выглядит следующим образом и обычно остается неизменным.
- Имеем уравнение x2−49=0 или аналогичное ему.
- Раскладываем его как (x-7)*(x+7)=0.
- Получаем решение типа x=7 и -7.
- Записываем ответ в виде двух корней.
В качестве примера возьмем следующее равенство: x2+18x = 0. Проанализируйте в форме x*(x+18) = 0. Вы получаете x = 0 и -18. Оба решения верны и согласуются с результатом. Решаются и другие выражения, связанные с бесконечными квадратными уравнениями такой формы.
Менее распространенный, но общий тип квадратного уравнения. Здесь есть два корня, которые отличаются только знаками, но в крайнем случае корней нет.
Особый вид уравнения
Рассмотрим следующий пример, который разрешает такие выражения.

Другие способы решения неполных уравнений
Если точки совпадают, то решения нет. Например, выражение 25 x 2 + 1 = 0 не имеет решения, потому что сумма положительных чисел никогда не может быть равна нулю.
На школьных уроках алгебры попытка решить эти уравнения приводит к виду x2 = d. Это означает, что 9 x 2-2 равно нулю. Тогда x2 = 2/9 и ответ — два одинаковых корня с разными знаками.
Существует также особый тип формулы сокращения. Существует ax2 следующего вида, который равен нулю. Такие уравнения имеют решения в виде единственного корня. Согласно школьным учебникам, решение состоит из двух корней, каждый из которых равен нулю.
Такие выражения квадрата можно решить без применения какого-либо вида квадратного корня. К таким типам решений относятся инкрементные типы умножения и правила деления чисел.
Предположим, что уравнение 5 x 2 = 0. Единственный ответ здесь — x=0, потому что в этом уравнении результат получается простым умножением на ноль.
Теперь возьмите уравнение вида 5 x 2 = 125. Разделите обе части уравнения на 5. Получаем следующий промежуточный результат: x2=25. Двигаясь влево, получаем x2-25=0. Затем используйте уравнение разности квадратов в виде (x-5)*(x + 5) = 0. Конечным результатом будет x = 5 или x = -5.
Теперь посмотрим, как решить уравнение 16*x2-x=0 с помощью вышеописанного метода. Общий множитель вычитается из скобки x*(16x-1)=0. Это дает два ответа x=0 и 16x=1. Затем каждая часть делится на 16, чтобы получить окончательный ответ x=1/16. Окончательные ответы записываются как x1=0 и x2=1/16.

Обратите внимание, что если вы не знаете, как разделить уравнение деления на число, то для решения таких уравнений лучше всего применять стандартные правила решения квадратных уравнений. Человек сам выбирает, какой метод использовать для решения этих квадратных уравнений. Самое очевидное решение может не сработать в конкретном примере, а конкретного ответа может вообще не быть. Кроме того, стандартные целые числа не всегда являются подходящим вариантом.
Если точки совпадают, то решения нет. Например, выражение 25 x 2 + 1 = 0 не имеет решения, потому что сумма положительных чисел никогда не может быть равна нулю.
Неполные квадратные уравнения

Неполные примеры квадратичного типа, несмотря на свое название, довольно легко решаются. Можно применять как обычные методы нахождения ответа, такие как квадратные корни, так и деленное умножение, а также деление на числа.

Виды неполных квадратных уравнений
Однако ни один из вышеперечисленных методов не является универсальным. Каждое конкретное уравнение имеет свой собственный метод нахождения ответа. Также обратите внимание, что не все квадратные уравнения имеют ответ, а некоторые могут вообще не иметь корней. Это тот случай, когда оба числа положительные и их сумма не может быть равна нулю.
Первый случай
Такие квадратные уравнения можно решить без применения квадратного уравнения. Законы сокращенного умножения и деления чисел называются такими решениями.
Неполные квадратные уравнения можно решить очень быстро. Главное — знать, как решается каждая подкатегория неполного уравнения. Всего их три, со своими известными путями решения. Попробуйте решить уравнение любого типа. Так вы можете быть уверены.
Каждый подтип уравнения решается быстро и легко. Главное — овладеть навыком преобразования уравнения, то есть переноса чисел из одной части тождества в другую и удаления общих элементов из скобок.<-с\over а>Для коэффициента b = 0. Затем следует выражение для неполного квадратного уравнения.
Решение в этом случае следующее.
$ x_2 =-\ sqrt
Второй случай
Обратите внимание, что под корнем $- могут находиться как положительные, так и отрицательные числа. Знак минус в данном случае просто указывает на обратное. Если результат под корнем — отрицательное число, то уравнение не имеет действительного корня.
$ 7x ^ 2-28 =0$- Перенесите -28 в правую часть уравнения с противоположным знаком.
$ x ^ 2 =28$ — Разделите обе части уравнения на 7.
Во втором случае коэффициент c равен нулю. Тогда уравнение становится
В этом случае решение несколько иное.
Третий случай
$ ax ^ 2 + bx = 0 $- Вычтите общий делитель из скобок (существует общий делитель x).
$ x (ax + b) = 0 $- Если один из множителей равен нулю, то произведение равно нулю.
Этот метод можно использовать при решении всего квадратного уравнения. Если уравнение разрушается с помощью одного из сокращений при умножении, то каждая скобка множителя равна нулю, и уравнение можно решить гораздо быстрее, чем при скромных способностях.
Третий случай — самый простой, когда B и C равны нулю. В этом случае оба корня всегда равны нулю.
Обратите внимание, что в любом случае необходимо проверить корни квадратного уравнения. Результат должен быть вычислен путем замены каждого корня результата на исходное уравнение.
Теорема Виета
Это особенно важно для неполных уравнений. Это происходит потому, что все думают, что это легко, и не акцентируют внимание на вычислениях. Это может привести к разного рода ошибкам. В большинстве случаев студенты путают знаки. Вместо + они получают — и наоборот. Помните, что эти символы очень важны и должны соблюдаться при переносе и делении чисел. Вы можете проверить сами, заменив типы значений, перечисленные в статье.
Коэффициент A может быть отрицательным. В этом случае нужно разделить на отрицательное число. Это означает, что все знаки в уравнении будут перевернуты. Обратите внимание на эти скользкие места.
Неполное квадратное уравнение AX² + Bx = 0 можно решить умножением. Уберите многочлен в левой части уравнения — удалите общий коэффициент X из скобки.
Но как насчет любимой теоремы Бето? Можно ли применить этот метод к неполным трем именам? Попробуем разобраться в аспекте редукции неполного уравнения в классической форме AX2 + BX + C = 0.
На самом деле, к этому случаю можно применить теорему Виета. Все, что вам нужно сделать, это свести уравнение к его общей форме, заменив недостающие условия нулями.
Например, если b = 0 и a = 1, то, чтобы избежать путаницы, уравнение следует записать так: ax2 + 0 + c =0. Тогда соотношение корней и множителей многочлена выражается так: a = 0, b = 0, a = 1, c = 0.
Теоретические доклады помогают ознакомиться с характером проблемы, и вы всегда должны уметь решать конкретные задачи. Опять же, обратитесь к справочнику по использованию, чтобы найти подходящие примеры.1Напишите формальное выражение, подходящее для применения теоремы Виетта.2Следующий шаг — создание терминологической системы.
Очевидно, что корнями квадратного многочлена являются x
= 4 и x
= -4.
Теперь давайте потренируемся сокращать уравнения в общем виде. Возьмем следующий пример: 1/4 x x 2-1 = 0
Как решить уравнение ax² + bx = 0
Чтобы применить теорему Виета к выражению, нужно удалить дроби. Умножьте левую и правую части на 4 и проверьте результат: x2-4 = 0. В правой части уравнения: x2 = 4.
В целом, лучшим способом решения неполных уравнений является факторизация, которая является самым простым и быстрым методом. Если возникают проблемы с поиском корней, можно прибегнуть к традиционному методу поиска корней через дискриминацию.
Обратите внимание, что в любом случае необходимо проверить корни квадратного уравнения. Результат должен быть вычислен путем замены каждого корня результата на исходное уравнение.
Когда C = 0, решением третьего вида неполных квадратных уравнений является остаток.
Квадратные уравнения без C не используются только для решения первого примера. Запоминание алгоритма значительно облегчает решение задач в книге.
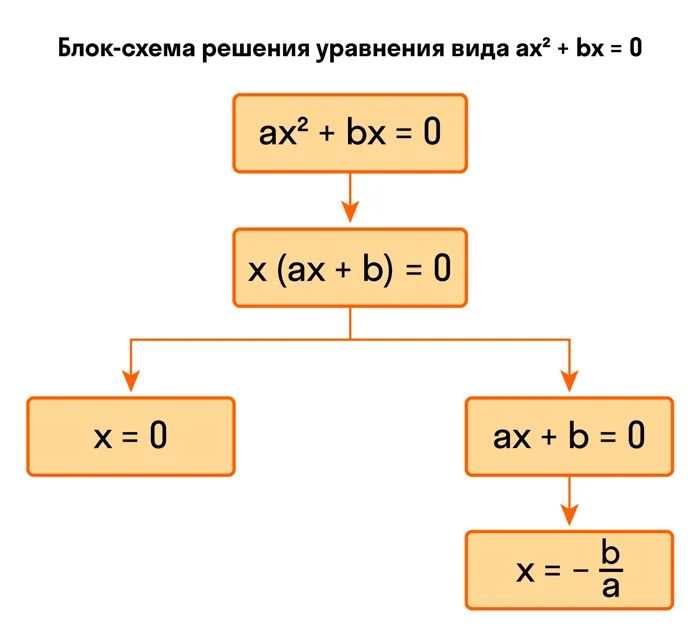
Неполное квадратное уравнение ax²+bx= 0 может быть решено методом факторизации. Возьмите наибольший общий делитель x из скобок и разложите многочлен в левой части уравнения.
Теперь вы можете перейти от исходного уравнения к эквивалентному уравнению x *(ax + b) = 0. Это уравнение эквивалентно совокупности двух уравнений x = 0 и ax + b = 0, причем последнее уравнение является линейным, корень x = -b/a.
Поэтому неполное квадратное уравнение ax²+ bx = 0 имеет два корня.
Пример 1. Решите уравнение 2x²-32x=0.








