МЕДИАНА — треугольника Линия (или ее часть в пределах треугольника)Соединение с верхней частью треугольника в середине противоположной стороны. Три М. треугольника пересекаются в одной точке, называемой центром тяжести. треугольника, Центр тяжести, или… … Энциклопедия математики
Медианы треугольника
Медиана треугольника — это отрезок, идущий от вершины треугольника в центр противоположной стороны. На рисунке 1 AM — медиана треугольника ABC (соединение вершины A с центром стороны BC, т.е. BM = MS ).
Любой треугольник имеет три медианы. На рисунке 2, AM, BC, SD. медианы треугольника ABC. Медиана AM соединяет вершину A с серединой стороны BC, точкой M ( BM = MC ), медиана BC соединяет вершину B с центром стороны AC — точкой K ( BC = KS ), медиана CD соединяет C с центром AB — точкой D ( AD = DB ).
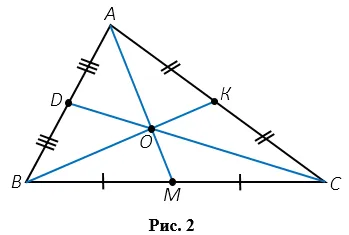
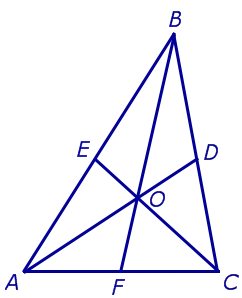
Замечательная недвижимость медиан треугольника: в любом треугольнике медианы пересекаются в одной точке. Рисунок 2 медианы ABC пересекается с точкой О. Таким образом, точка О делит каждый медиану в соотношении 2 : 1, рассчитанном от вершины, т.е. AO : OM = BO : OC = CO : DO = 2 : 1.
В любом треугольнике Можно определить три момента медианы. Если мы нарисуем их точно, то в каждом треугольнике медианы они пересекаются в одной точке
Свойства
- Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами в шести равных треугольников.
- Большей стороне треугольника соответствует меньшему медиана.
- Из векторов, образующих медианы, можно составить треугольник.
- При аффинных преобразованиях медиана переходит в медиану.
- Медиана треугольника делит его на две равновеликие части.
-
(выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- Формула стороны через медианы:
Если две медианы перпендикулярны друг другу, то сумма квадратов сторон, на которые они падают, в пять раз больше квадрата третьей стороны.
Мнемоническое правило
Медианная обезьяна с острым глазом перепрыгивает в точный центр стороны, противоположной вершине, где она теперь стоит.
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Медиана треугольника» в других словарях:
Медиана (понятия) — Медиана: Медиана треугольника в планиметрии — отрезок, соединяющий вершину треугольника до середины противоположной стороны в статистике медианой это значение в популяции, которое делит ряд данных пополам Медиана (статистика) … … Википедия
Медиана — Медиана. треугольника В планиметрии отрезок, имеющий вершину треугольника к среднему значению противоположной стороны Медиана (статистическая) квант 0,5 Медиана (кривая) средняя линия кривой, проведенной между правой и левой … Википедия
Медиана (геометрия) — Треугольник и его медианы. Медиана треугольника ― отрезок внутри треугольника, соединение вершины треугольника с серединой противоположной стороны, а также Строка, содержащая данный раздел. Содержание 1 Свойства 2 Типы … Википедия
CENTER — это линия, соединяющая вершину треугольника до середины основания. Полный словарь иностранных слов, употребляемых в русском языке; Попов М., 1907. медиана (Lat. mediana mediana) 1) геологический разрез, соединяющий вершину. треугольника с. … Словарь иностранных слов в русском языке
Медиана (в геометрии) — Медиана (от лат. mediana median) в геометрии, отрезок, соединяющий одну из вершин треугольника в середине противоположной стороны. Три М. треугольника пересекаются в точке, которую иногда называют «центром тяжести». треугольника, так …Большая советская энциклопедия
МЕДИАНА — треугольника Линия (или ее часть в пределах треугольника)Соединение с верхней частью треугольника в середине противоположной стороны. Три М. треугольника пересекаются в одной точке, называемой центром тяжести. треугольника, Центр тяжести, или… … Энциклопедия математики
МЕДИАНА — (от лат. mediana середина) отрезок, соединяющий вершину треугольника До середины противоположной стороны … Большой энциклопедический словарь
МЕДИАНА — MEDIANA, медианы, Женщина. (лат. mediana, буквально — срединный). 1. прямая линия от вершины треугольника к середине противоположной стороны (мат.); 2. в статистике, для набора многих данных, величина, обладающая тем свойством, что количество данных, … … Словарь Ушакова
МЕДИАНА — МЕДИАНА, с., женский род. В математике отрезок прямой, соединяющий вершину треугольника в середине противоположной стороны. Словарь Ожегова. С. Ожегов, Н. Шведова. 1949 1992 … Словарь Ожегова
MEDIANA (секция) — MEDIANA (от лат. mediana середина), секция, соединяющая вершину. треугольника с серединой противоположной стороны … Энциклопедический словарь
Медиана (геометрия) — Треугольник и его медианы. Медиана треугольника ― отрезок внутри треугольника, соединение вершины треугольника с серединой противоположной стороны, а также Строка, содержащая данный раздел. Содержание 1 Свойства 2 Типы … Википедия
Медиана треугольника
Определение. Медиана треугольника это отрезок, выходящий из вершины треугольника до середины противоположной стороны (Рисунок 1).
Поскольку в каждом треугольнике Если есть три вершины, то каждая треугольнике можно провести три медианы.
На рисунке 1 медианой является сегментом BD .
Утверждение 1. Медиана треугольника делит его на два треугольника равна площади ( равна. треугольника).
Доказательство. Проведем из вершины B треугольника ABC медиану BD и высотой BE (рис. 2),
и отметить, что (см. раздел в нашем справочнике по региону. треугольника»)
Поскольку секция BD медианой, то
должны быть доказаны.
Утверждение 2: Пересечение любых двух медиан треугольника разделяет каждого из них медиан в соотношении 2 : 1, рассчитанном от вершины. треугольника.
Доказательство. Рассмотрим любые два медианы треугольника, например, медианы AD и CE, и обозначим их пересечение через O (рис. 3).
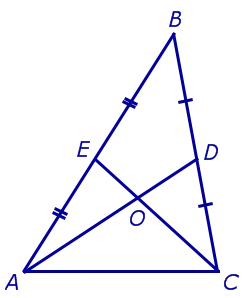
Обозначим средние значения сегментов AO и CO через F и G соответственно (рис. 4).
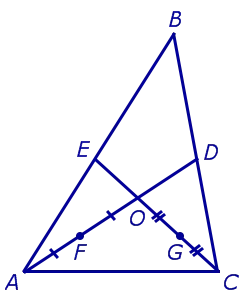
Теперь рассмотрим четырехугольник FEDG (рисунок 5).
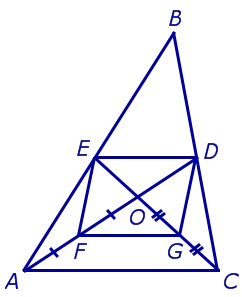
Сторона ED этого четырехугольника является средней линией в треугольнике ABC. Следовательно,
Сторона FG четырехугольника FEDG является средней линией. в треугольнике AOC. Следовательно,
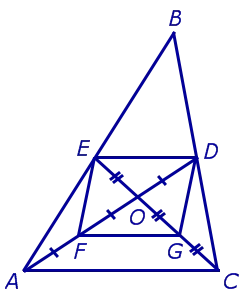
Отсюда следует, что точка O каждого из медиан AD и CE в соотношении 2 : 1, вычисленные из вершины треугольника.
Следствие. Все три медианы треугольника которые расположены по адресу .
Доказательство. Рассмотрим медиану AD треугольника ABC и точка O, которая является эту медиану в соотношении 2 : 1, измеряется от вершины A (рис. 7).
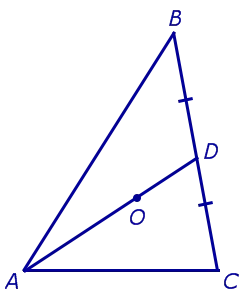
Поскольку точка, делящая отрезок в заданном соотношении, является единственной, остальные точки медианы треугольника пройдет через эту точку, что и будет доказано.
Определение. Точка пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3: Диаметр. треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство. Доказать, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна площади треугольника ABC. Для этого вам следует, напр, треугольник AOF и опустите перпендикуляр AK из вершины A на прямую BF (рис. 9).
Если рисунок из той же вершины медиану, биссектриса угла, а высота то медиана наибольший сегмент, а высота — наименьший сегмент.
Медиана треугольника
Медиана треугольника — это отрезок, который имеет вершину треугольника в середине противоположной стороны.
Как построить медиану треугольника?
Чтобы построить медиану треугольника, надо:
1) Найдите и отметьте линейкой центр стороны. треугольника.
2) Соедините полученную точку с вершиной, противоположной этой стороне.
Рисунок медианы треугольника:
Как построить медиану треугольника Использование компасов и линеек без масштаба будет обсуждаться позже в разделе «Конструирование». треугольник».
Сколько медиан имеет треугольник?
Так как у треугольника три вершины и три стороны, отрезков, соединяющих вершину и центр противоположной стороны, также три. Итак, треугольник имеет три медианы .
Все три медианы треугольника они пересекаются в одной точке:
Точка пересечения медиан так называемый центр тяжести треугольника .
В точке пересечения медианы треугольника делится в соотношении два к одному, считая от вершины:
 Характерные особенности медианы.
Характерные особенности медианы.
Медиана разделяет треугольник на два треугольника с равной площадью.
Медианы треугольника Они пересекаются в одной точке, которая делит каждую из них в соотношении 2:1, начиная с вершины. Эта точка определяется как центр тяжести треугольника.
Весь треугольник можно разделить его медианами на шесть равных треугольников.








