Пример. Красные шапочки и волки любят пироги. Волк может съесть 24 пирожных за 4 часа, а рыжий — 35 пирожных за 7 часов. У волков в корзине 30 пирожков, а у рыжих — 20.
Задачи на совместную работу
Совместные задачи обычно начинаются в 4 классе и в основном решаются с помощью дробей, которые дети 4 класса не знают. Однако эти проблемы часто возникают на олимпиаде 4 класса и на вступительных экзаменах 5 класса. В данном разделе показано, как решать эти задачи без дробей.
Уравнения и уравнения используются для решения задач кооперации. Использование уравнений для решения задач четвертого курса спорно, но без них невозможно.
Совместные обязательства различны. Они включают группы рабочих, выполняющих одну и ту же работу, трубы, заполняющие и осушающие бассейны, траншеи, которые роют экскаваторы, и т.д.
Принципы решения проблем совместной работы схожи с принципами решения проблем движения. В проблемах движения маршруты являются продуктом скорости и времени.
Распространенной проблемой, связанной с работой, является объем проекта, соответствующий расстоянию, которое необходимо пройти, рассчитанный как скорость производства проекта (скорость заполнения водой бассейна, рытье траншеи и т.д.). Время.
В задачах движения скорости двух объектов, движущихся навстречу друг другу, суммируются, и как только один объект достигает другого, скорость сближения определяется как разность между скоростями двух объектов.
Аналогично, в задачах совместной работы скорости работы прибавляются и отнимаются, когда работа идет в одном направлении и когда работа идет в противоположном направлении. Например, если две трубы наполняют бассейн с определенной скоростью, а время, необходимое для наполнения бассейна двумя трубами, складывается из скорости каждой трубы. (У них одна и та же цель. Другими словами, они выполняют одну и ту же задачу).
Если определенное количество воды поступает в бассейн из одной трубы с определенной скоростью, а выходит из другой трубы с другой (более медленной) скоростью, то для определения времени заполнения бассейна необходимо отнять скорость первой трубы от скорости второй трубы. Это пропорционально тому, когда более быстрый объект достигает более медленного объекта. У них разные цели — один хочет уйти от погони, другой — догнать, и их скорость удаляется. Аналогично, у двух трубок разные цели — одна хочет наполнить бассейн, а другая — опустошить его.
Давайте рассмотрим конкретный пример.
Задача 1
Две трубы наполняют бассейн. Один из них имеет объем 5 литров в минуту, а другой — 10 литров в минуту. Объем бассейна составляет 300 литров. Сколько времени требуется двум трубам, чтобы заполнить бассейн?
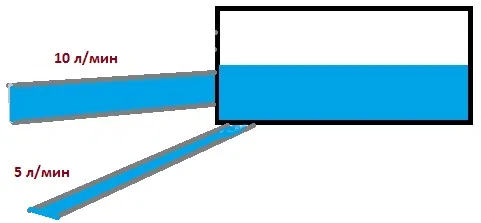
Добавьте скорость, с которой первая труба наполняет бассейн, к скорости второй трубы, чтобы найти общую скорость, поскольку эти две трубы выполняют одну и ту же задачу.
Известен объем бассейна — 300 литров. Поэтому, чтобы узнать, сколько времени потребуется для заполнения бассейна, нужно разделить объем бассейна на найденную скорость заполнения.
Ответ: бассейн будет заполнен через 20 минут.
Задача 2
Первоначально в лицензионный бассейн объемом 400 литров вода поступает из трубы со скоростью 30 литров в минуту. Из второй трубы, которая меньше по диаметру, вода выходит из бассейна со скоростью 20 литров в минуту. Сколько времени требуется для заполнения бассейна?
В этом случае трубки совершают противоположную работу, поэтому для получения конечной скорости необходимо вычесть наименьшую скорость из наибольшей.
10 л/мин — это конечная скорость заполнения бассейна. Если вы наливали в бассейн 30 литров воды в течение одной минуты и за ту же минуту вылили из бассейна 20 литров, у вас останется только 10 литров — это скорость наполнения.
Находим время для заполнения бассейна водой таким же образом, как и в первой задаче:
Ответ: Бассейн заполнится через 40 минут.
Если мы попытаемся, например, толкнуть стену, стена не сдвинется с места, и, следовательно, работа не будет совершена, поскольку сила была приложена, но она не вызвала никакого движения стены.
Математика по полочкам
Такие проблемы всегда имеют одни и те же значения, которых три. Время обозначается t. — Вторая величина — это объем работы: сколько деталей сделано, сколько воды вылито, сколько полей вспахано и так далее. По сути, это и есть скорость труда. Обозначим производительность буквой P.
Скорость выполнения любой работы, то есть производительность, можно определить как количество работы, выполненной за определенный промежуток времени. Вы получаете формулу продуктивности.
例。 Токарь делает 5 штук за час. Сколько изделий он сделает за 7 часов?
例。 Токарный станок производит 5 деталей в час. Он должен будет изготовить 20 изделий. Сколько времени ему потребуется для выполнения работы?
Пример. Красные шапочки и волки любят пироги. Волк может съесть 24 пирожных за 4 часа, а рыжий — 35 пирожных за 7 часов. У волков в корзине 30 пирожков, а у рыжих — 20.
Определите представление волка и Красной Шапочки. Волк съест 24 пирога (объем работы) за 4 часа (время). Таким образом, его производительность составляет P = O:t = 24:4 = 6 пирожков в час. Производительность красного волка: P = O:t = 35:7 = 5 пирожков в час. Давайте подсчитаем, сколько времени каждый человек потратит на свои пироги. У волка 30 пирожков. Таким образом, он тратит время: t = O:P = 30:6 = 5 часов. Красная Шапочка потратила на свои 20 пирожных: t = O:P = 20:5 = 4 часа. Красная Шапочка опережает Волка на один час. Ответ: Красная Шапочка.
Как определить производительность в следующих задачах: — Труба заполняет бассейн за 3 часа. (объем работы — бассейн — 1 бассейн); — строительная бригада строит дом за 150 дней. (объем работы — дом — 1 дом),
— трактор вспахивает поле за 12 часов. (количество работы — поле — 1 поле). Поэтому в задачах количество работы равно 1.
Задачи на совместную работу
Совместная работа возникает, когда несколько человек (бригад, насосов, тракторов и т.д.) выполняют одну и ту же задачу вместе и работают с разной скоростью.
例。 Труба может заполнить бассейн за четыре часа. Вторая труба занимает шесть часов. Сколько времени потребуется для наполнения бассейна, если обе трубы включить одновременно?
Поскольку трубки работают вместе, сложите их мощности. Для первой трубы, которая заполняет 1 бассейн за 4 часа: P = O:t = 1:4, т.е. за 1 час первая труба заполняет 1/4 бассейна. Для второй трубки: P = O:t = 1:6, т.е. вторая трубка заполняет 1/6 часть бассейна за один час. Вместе, при совместной работе, трубы заполнятся за один час: 1/4 + 1/6 = 5/12 — две трубы за 1 час. Рабочий объем составляет 1 пул. Совместная производительность составляет 5/12 бассейна в час. t = O:P = 1 : 5/12 = 12/5 = 2,4 (ч.) Ответ: 2,4 часа.
УПРАЖНЕНИЯ
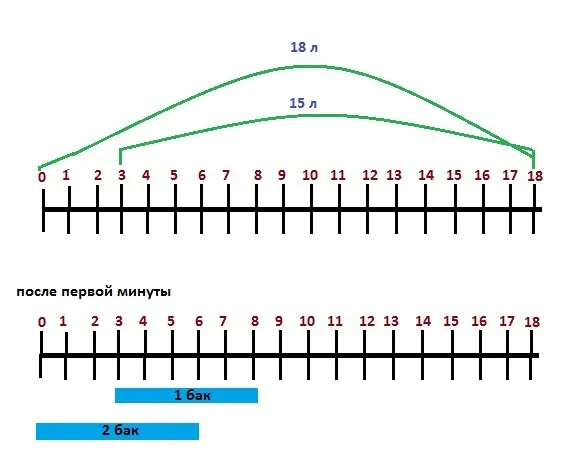
1. a) Одна труба наполняет бассейн за 3 часа, а другая — за 5 часов. Сколько времени потребуется для заполнения бассейна, если две трубы работают одновременно? Выберите правильное значение:.
(b) Один насос наполняет резервуар за 4 часа, а другой — за 2 часа. Если два насоса работают одновременно, сколько времени потребуется для заполнения бака? Выберите правильное значение: a) Сколько времени потребуется для заполнения бака, если два насоса работают одновременно?
(a) Емкость первой трубки равна 1/3, а емкость второй трубки равна 1/5. Общая мощность составляет 1/3 + 1/5. Чтобы найти время, затраченное на совместную работу, разделите объем работы — 1 на мощность: 1: (1/3+1/5).
2. a) Два строителя собрали стену за 10 дней, один из них мог бы выполнить работу за 16 дней. За сколько дней второй мог бы выполнить эту работу? Выберите правильное значение:.
(b) Кишечник может работать вместе за 8 часов, рукопись — за 12 часов 2 часа. Сколько часов может занять работа второго поселенца? Выберите правильное значение:.
Решение: a) Производительность первого производителя составляет 1/16 часть от общей производительности. Доходность второго строителя составляет от 1/10 до 1/16. Чтобы найти время, затраченное вторым строителем, разделите нагрузку-1 на производительность: 1: (1/10-1/16). Ответ: 2.
3. a) Отец выполняет всю работу за 4 часа, а сын — за 7 часов. Какой объем работы они выполняют за 1 час? (b) Мама делает всю работу за 1 час, а дочь — за 2 часа. Какой объем работы они выполняют за 1 час? Решение: a) Отцы имеют производительность 1/4, а сыновья — 1/7. (a) Производительность отца составляет 1/4 + 1/7 = 11/28% от часовой работы. Ответ: 11/28 работа. 4.(a) Если шесть рядов работают одновременно, все поле скашивается за 14 часов. Нужно ли 8 часов, чтобы очистить поле? (b) Если 7 раров работают одновременно, то для очистки поля потребуется 14 часов. На уборку поля уходит 10 часов? Решение: а) 1) 6*14 = 84 (h) — для уборки всего поля требуется береговая машина. (2) 84:8 = 10,5 (h) — для скашивания всего поля необходимо 8 косилок. Ответ: 10,5 (h) 5. a) 18 студентов, работающих по 6 часов в день, захватывают все поле. Сколько студентов необходимо для одновременного овладения полем, если они работают по 9 часов в день? (b) 12 студентов, работающих по 8 часов в день, захватывают все яблоки во фруктовом саду. Сколько студентов должны собрать все яблоки во всех садах одновременно, если они работают один день? Решение: а) 1) 6*18 = 108 (h) — для того, чтобы напрячь все поле, нужны студенты. (2) 108:9 = 12 (ст.) — требуется ученик, чтобы захватить все поле, работая 9 часов в день. Ответ: 12 студентов. 6.(a) Производительность дочери и матери относится 2:3. Когда они работают вместе, то забывают об огороде за 12 часов. Когда они работают отдельно, сколько часов каждый убирает огород? (b) Производительность труда отца и сына относится как 3:5. Партнеры работают в течение 15 часов. Сколько часов каждый из них работает отдельно?
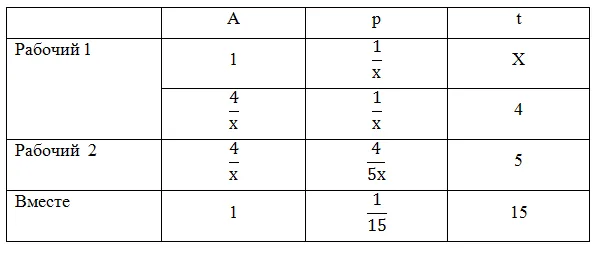
Решение: a) При X как коэффициенте пропорциональности, дочь работает в два раза продуктивнее, а мать — в три раза. Производительность при совместной работе равна 2x + 3x = 5x. Объем работы составляет 12*5x = 60x. 1) 60x: 2x = 30 (h) — дочь тратит. 2) 60x: 3x = 20 (h) — потрачено матерью. Ответ: 30 (ч) — 20 (ч). 7.(a) Согласно плану, типографии требовалось 15 дней для печати учебников. Однако за три дня до окончания срока дизайнер типографии уже выполнил план, печатая по 2 000 учебников каждый день, перевыполняя план. Сколько книг напечатал принтер? (b) Машинному цеху требуется 30 дней для выполнения заказа. Однако за три дня до срока завод перевыполнил план и производил по три машины в день, тем самым выполнив заказ. Сколько машин произвел завод? Решение: предположим, что (a) X книг в день печаталось по плану, но было напечатано X+2000 книг в день. (1) 15-3 = 12 (дней) — принтеры, потраченные на выполнение заказа. 15x — количество заказанных книг, а 12 (x+2000) — количество напечатанных книг. Эти величины равны. Составим уравнение для решения: 15х = 12 (х+2000), 15х = 12х+24000, 3х = 24000, х = 8000 (м) — принтер должен был печатать. (2) 8000*15 = 120000 (м) — распечатано принтером. Ответ: 120 000 (м) книг.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. два экскаватора разной мощности роют котлован. Работая отдельно, первый может вырыть котлован за пять дней, а второй — за семь. Работая вместе, за сколько дней они выкопают котлован? Выберите правильные значения:.
1) (7+5): 2; 2) 1: (7+5); 3) 1: (1/7+1/5). 2. одна труба заполняет бассейн за 3 часа, а другая — за 5 часов. Если две трубы открыты одновременно, сколько часов потребуется для наполнения бассейна? Напишите выражение для решения задачи.
3. два экскаватора роют траншею. Работая отдельно, первый мог вырыть траншею за 10 дней, а второй — за 16 дней. Когда они работают вместе, сколько дней им потребуется, чтобы вырыть траншею?
4. водоем заполняется из первой трубки за 5 часов, а из второй трубки за 4 часа. Сколько часов требуется для заполнения бака, если две трубы работают вместе?
5. необходимо напечатать два компонента, каждый из которых содержит 120 страниц. Вторая машинистка напечатала за один час на пять страниц меньше, чем первая, и закончила работу через два часа. Сколько страниц в час у первого поселенца?
6. две группы рабочих произведут 240 компонентов. Первая команда работала 6 часов, а вторая — 5 часов. Если первая группа производила на 4 компонента в час больше, чем вторая, то сколько компонентов в час производила каждая группа?
7. план предусматривает, что группа ежедневно выбрасывает 20 га. После начала сева «Колхоз» ежедневно засевал на 5 га больше, чем планировалось, поэтому сев был завершен на два дня раньше запланированного срока. Определите площадь для посева.
8. два строителя установили стену за 20 дней. Если известно, что первому пришлось работать на 9 дней больше, чем другому, то сколько дней нужно каждому из них для выполнения работы по отдельности?
9. судно оборудовано кранами. Три крана одинаковой грузоподъемности работали в течение четырех часов, затем добавили еще два крана, и через три часа груз был завершен. Если все краны начинают работать одновременно, груз будет выполнен за шесть часов. Сколько времени требуется меньшим и большим кранам, работающим вместе, чтобы завершить погрузку?
10. вода из трех кранов заполнила бак за 12 минут и 40% бака после того, как первый кран был открыт в течение 4 минут Если вы знаете, что второй кран выбрасывает воды за 6 минут столько же, сколько третий кран за 5 минут, наполняет ли каждый кран бак?
Определите, сколько времени потребуется мастеру для покраски забора. Используйте этот тип для поиска времени. Разделите количество выполненной работы на общее производство ремесленника. Количество выполненной работы выражается единицей и производительностью.
Как решать задачи на работу: основные правила
При решении задачи необходимо соблюдать следующие правила
- Если работу выполняют двое рабочих, то их производительности складываются
- Если объем работы в задаче не задан и нет данных, позволяющих его найти, и при этом объем работы не важен для решения задачи, то работа принимается за единицу.
- За переменную Х, как правило, удобнее всего брать производительность
Решение задачи на работу: 3 простых шага
Решение рабочей проблемы включает в себя три этапа.
- Задаем переменную Х и составляем таблицу
- Составляем уравнение на основании таблицы и условий задачи, решаем его
- Возвращаемся к условиям задачи, вспоминаем, что требовалось найти и находим ответ
Помните о третьем шаге. Это происходит потому, что учащиеся, исправив уравнение, сразу записывают ответ задачи и забывают, что им нужно было найти по условиям задачи. На самом деле, правильно решенная проблема не получит той оценки, которую она заслуживает.
Примеры решения задач на работу: от простого к сложному
Задача 1
Первый рабочий выполняет заказ из 120 компонентов на два часа быстрее, чем второй. Известно также, что первый рабочий производит на три компонента в час больше, чем второй. Сколько компонентов собирает первый рабочий в час?
1. создайте таблицу, основанную на рассматриваемых условиях. Производительность первого рабочего равна x. Производительность второго рабочего равна x — 3, потому что второй рабочий собирает на три компонента меньше, чем первый. Время выполнения всех задач возникает в результате разделения всех задач по производительности. 2. мы также знаем из рассматриваемых условий, что вся работа (120 деталей) выполняется на 2 часа быстрее, чем первым работником на 2 часа. Таким образом, мы имеем следующее уравнение Решите уравнение. Для этого приведите все дроби к общему знаменателю.
120x -360 + 2x 2-6x -120x = 0
Разделите обе части уравнения на 2.
3. вернуться к условиям проблемы. Нам нужно было узнать количество изделий, изготовленных первым рабочим. Это цена, обозначенная x.2 Это не соответствует концепции проблемы. Таким образом, первый рабочий производит 15 компонентов в час.
Задача 2
Первая трубка заполняет 180-литровый резервуар, а вторая — 120-литровый. Известно, что одна из труб вмещает на один литр меньше воды, чем другая. Если резервуары заполняются одновременно, необходимо определить количество литров в минуту, которое проходит первая трубка.
1. создайте таблицу, основанную на рассматриваемом условии. Укажите пропускную способность первой трубки, т.е. количество воды, которое проходит через нее за одну минуту при температуре X. Тогда производительность второй трубки составит 1 литр в минуту или 1 литр в минуту. Его можно обозначить как X ± 1. Рассчитайте время в соответствии с типом и занесите его в таблицу.
2Из условий задачи известно, что обе трубы выполняют работу одновременно. Следовательно, мы можем приравнять время работы первой трубки к времени работы второй трубки, поэтому: решите два уравнения; решите первое уравнение; решите второе уравнение; решите третье уравнение; решите четвертое уравнение. Решите первое уравнение.
3. вернуться к условиям проблемы. Необходимо было определить количество литров в минуту, которое пропускает первая трубка. Это емкость первой трубки, обозначенная x.2 Это не соответствует смыслу проблемы. Таким образом, первая трубка пропускает через себя 3 литра в минуту.
Задача 3
Первая труба пропускает на 5 литров воды в минуту больше, чем вторая. Определите количество литров воды в минуту, которое проходит первая трубка, если известно, что для наполнения бассейна объемом 300 литров ей потребуется на 3 минуты больше времени, чем второй трубке.
1. создайте таблицу, основанную на рассматриваемых условиях. Обозначьте емкость второй трубки символом X. Тогда производительность первой трубы X равна 5, так как она пропускает 5 литров воды в минуту. Объем таза (который является объемом трубы в трубе) равен 300 литрам. Время работы трубы определяется типом и заносится в таблицу.









