Понятие математического ожидания можно рассмотреть на примере с бросанием игрального кубика. При каждом броске фиксируются выпавшие очки. Для их выражения используются натуральные значения в диапазоне 1 – 6.
Математическое ожидание
Рассмотрим произвольное вероятностное пространство $(⌘ omega ,, f(x))$. Здесь $ f(x)$ — функция распределения случайной величины $ \ xi = \ varphi(⌘ omega)$.
Математическое ожидание случайной величины $ \ xi = \ varphi (⌘ omega)$ является действительным числом
$ mxi = \ int \ пределы _<\omega \in \Omega >\ varphi(\ omega)p(d \ omega)$, (1)
Если существует интеграл в (1), называемый интегралом Лебега, то ожидания существуют (насколько определены случайные величины и измерения Лебега).
Главный недостаток интеграла Лебега заключается в том, что в общем случае неясно, как его вычислить. Однако благодаря тому, что он существует, это, вероятно, единственный способ записать их, единственный способ получить тип. Именно поэтому при вычислении интегралов Лебега часто используются интуитивные подходы.
Если случайные величины различны, то интегрирование (14) имеет вид
$ \ int \ пределы _<\omega \in \Omega >\ varphi(\ omega)p(d \ omega)= \ сумма \ пределы _<\omega \in \Omega >\ p(\ omega)$, ($ \ сумма \ пределы _<\omega \in \Omega >p(\ omega)= $ 1), (2)
Предполагается, что ряд полностью сходится. В противном случае считается, что интеграции, а значит и ожиданий, нет.
Таким образом, если различные случайные величины $ \ xi $ задаются серией присваиваний, то матожидание вычисляется по типу
$ m \ xi = \ сумма \ пределы _^x_ \ cdot p_ $ или $ m \ xi = \ сумма \ пределы _^<\infty >x_ \ cdot p_ $, (3)
Соответственно, числовая последовательность в правой части второго типа (когда дискретная случайная величина имеет измеримое число значений) сходится.
Если мера вероятности определена на действительных осях, определяемых функцией распределения, то она непрерывна и
$ \ int \ пределы _<\omega \in \Omega >\ p(d \ omega) = \ int \ пределы _
Готовые работы на аналогичную тему
$ f_ функции.<\xi >(x)$ различна (говорят, что непрерывна), как показано в (13)
Ожидания возможны, если правая часть (5) неполярного интегрирования сходится. Если правая часть (5) не погружается в намерения, то для случайной величины $ \ xi $ не существует конечных ожиданий.
Наблюдение. Типы (1), (2) и (4) здесь не используются. Информация, содержащаяся в них, является теоретической.
Свойства математического ожидания
Всегда предполагается, что случайные величины $ \ xi $ и $ \ eta $ определены в одном и том же вероятностном пространстве.
$ m(c \ cdot \ xi) = c \ cdot m \ xi $ если $ c = const $.
$ m (Lo_ c cdot \ xi \ pm \ eta) = m \ xi \ pm m \ eta $ произвольные случайные величины $ \ xi $, $ \ eta $.
Если математическое ожидание $ m \ xi $ существует $ m \ eta $, то существует $ m(ᢙ xi \ pm \ eta)$.
Если математическое ожидание $ m \ xi $ существует $ m \ eta $, то $ m(\ xi \ cdot \ eta)$ существует.
Геометрически матожидание численно равно дальнему центру тяжести интеграла (5).
Применение на практике
Симметричная валюта бросается дважды, а симметричные кости — один раз. Найдите среднее количество очков, если «суд» стоит $400, а «сетка» — $400. Проверьте свойства математического ожидания для $3 и $4.
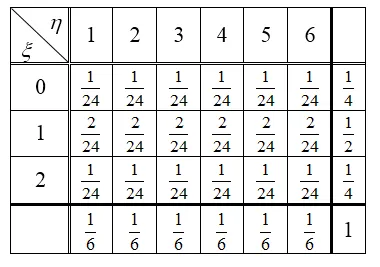
Решение. Пространство в элементарном событии броска двойной валюты состоит из 4 точек $ \ омега _ = \< (0,0),(0,1),(1,0),(1,1)\>$, а пространство элементарных событий в простом броске игральной кости состоит из 6 точек $ \ omega _ = \.< (1),(2),(3),(4),(5),(6)\>$. $ \ omega = \ omega _ \ cdot \ omega _ $ состоит из $ 4 \ cdot 6 = 24 $.
Учитывая симметрию между валютой и игральными костями, воспользуемся классическим подходом. Придайте каждому элементарному событию вероятность 400/24 $.
Предположим, что $ i $ 1, $ i = $ 0,1,2, и $ \ xi $ идентифицирует $ \ eta $ как случайные величины. $ 4.5.6. предположим, что случайные величины $ \ xi $ и $ \ eta $ независимы (следовательно, $ p_ = p_ \ cdot p_ $). Таблица 3 (рис. 1), ячейка содержит возможности $(Lo_ xi, Lo_ eta)$.
Свойство 3. a) $ m(ɛ xi + ɛ eta) = \ sum limits _^{ sum limits _^(x_ +y_)ɛ cdot p_ = \ left ((0 +1)ɛ cdot \ frac \ rid. +$
\+(0+2)Ј cdot \ frac+(0+3)Ј cdot \ frac+(0+4)Ј cdot \ frac+(0+5)Ј cdot \ frac+Ј left. (0+6)Ј cdot \ frac+ (0+6)Ј cdot \ frac+ (1+2)Ј cdot \ frac+ (1+3)Ј cdot \ frac+ справа.(1+4)Ј cdot \ frac+ (1+5)Ј cdot \ frac+ слева. (2+2)팀 cdot \ frac+ (2+3)팀 cdot \ frac \ справа.+팀 cdot \ frac+ (2+4)팀 cdot \ frac слева. \ frac \ справа) = \ frac \ cdot (1+2+3+4+5+\+6) +\ frac \ cdot (2+3+4+5+6+7) +\ frac \ cdot (3+4+5+6+7+8) = \ \ \ \ = \ frac+\ frac = \ frac = 4.5 \
(b) $ m \ xi = 0 \ cdot \ frac +1 \ cdot \ frac +2 \ cdot \ frac = \ frac +\ frac = 1> 0 $,.
)
Свойство 4. a) $ m(\ xi \ cdot \ eta) = \ sum \ limits _^\ sum \ limits _^x_ \ cdot y_ \ cdot p_ = \ left (1 \ cdot 1 \ cdot \ frac +1 \ cdot 2 \ cdot \ frac \ right: +$.
\ (\ +3) 1) frac 2 \ cdot 4 \ cdot 5 \ cdot 5 \ frac +2 \ cdot 6 \ cdot 6 \ frac \ right) = \ frac \ cdot (1+2+3+4+\+5+6) +슰 frac \ cdot (2+4+6+8+10+12) = \ frac+슰 frac = \ 3.5, Ј
$ m (ɑ xi \ cdot \ eta) = m \ xi \ cdot m \ eta = 1 \ cdot 3.5 = 3.5 $ (удовлетворяет свойству 4).
Куртозис — это величина, характеризующая кривизну функции плотности вблизи точки максимума. С научной точки зрения, это мера кислотности верхней части плотности распределения случайной величины.
Математическое ожидание
Математические ожидания — это ожидаемый результат определенного количества энергии.
Например, ожидаемая стоимость инвестиций может быть рассчитана на определенный момент в будущем. Расчет математических ожиданий перед инвестированием позволяет инвестору выбрать наилучший сценарий, который, по его мнению, даст наилучший результат.
Существует два типа случайных величин.
- Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
- Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.
Математическое ожидание отдельной случайной величины вычисляется по следующему виду
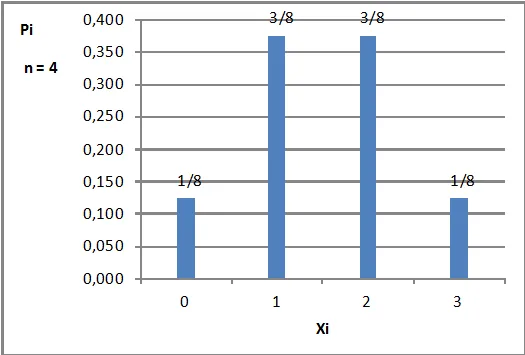
m(x) = ∑ xi×pi, где m — математическое ожидание, x — случайная величина, а p — вероятность случайной величины.
Математическое ожидание отдельной случайной величины рассчитывается следующим образом: 1. Сначала умножьте каждый из возможных исходов на его вероятность (например, вероятность выпадения «1» равна 1/6, а «2» — 1/3). Поэтому умножьте 1 на 1/6, 2 на 1/3 и т.д. 2. Затем сложите все эти значения (1 x 1/6 + 2 x 1/3 и т.д.).
Для непрерывных случайных величин используется этот тип.
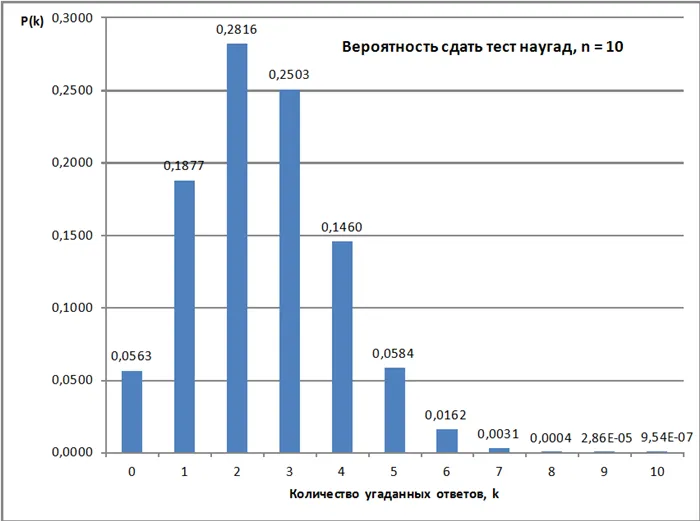
m(x) = ∫ f(x) x x.dx где m — ожидаемая f(x) — функция (заданная в рассматриваемом договоре) x — случайная переменная dx — выполненный элемент
В этом случае интегрирование рассчитывается в этой точке.
Примеры вычисления математического ожидания
- если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
- если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.
Пример 1
Следующие данные используются для вычисления ожиданий для различных случайных величин x.
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Этот тип использовался для отдельных случайных величин.

m(x) = ∑ xi x pi = -1 x 0,1 + 1 x 0,2 + 2 x 0,3 + 3 x 0,1 + 4 x 0,3 = -0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найдите ожидание величины x, которая постоянно распределена с плотностью f (x) = 2x, x ∈ (0.1) и f (x) = 0.
Для непрерывных случайных величин использовался тип:.

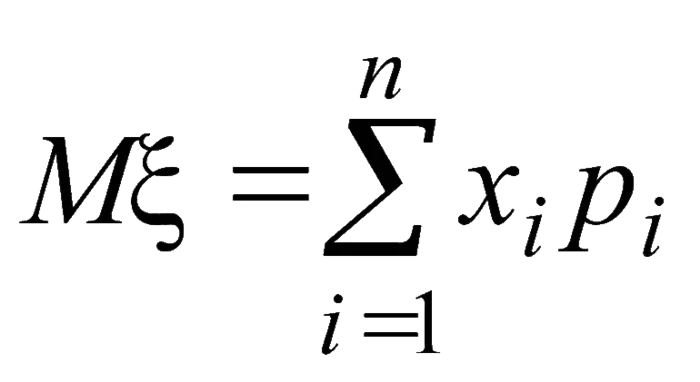
Пример 3
Следующие данные используются для вычисления ожиданий для различных случайных величин x.
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Этот тип использовался для отдельных случайных величин.

m(x) = ∑ xi x pi = 1 x 0,3 + 2 x 0,3 + 3 x 0,1 + 4 x 0,1 + 5 x 0,2 = 0,3 + 0,6 + 0, 3 + 0,4 + 1 = 2,6
Пример 4
Найдите математическое ожидание величины x, которая постоянно распределена с плотностью f(x) = (1/10).
Пример 4. 100 фиксированных кнопок классифицируются как стулья. Вероятность падения кнопки вверх на ребро равна 0,4. Найдите среднее число, вариацию и среднеквадратичное значение числа упавших вверх кнопок. Используйте три правила Сигмы, чтобы найти предполагаемый интервал количества этих кнопок.
п.3. Дисперсия
Изменение различных случайных величин x = xI.>математическое ожидание квадратического отклонения случайной величины математическое ожидание: $ \ mathrm< D(X)=M(X-M(X))^2 >На практике вариации рассчитываются с помощью $ \ типа mathrm.< D(X)=M(X)^2-M^2(X)=\sum_^n x_i^2p_i-M^2(X) > $
Свойства диаспоры 1) Размерность дисперсии равна квадрату размерности случайной величины. 2) Вариации могут быть неотрицательными действительными числами. 3) Постоянная вариация равна нулю.
4) Вариация суммы независимых случайных величин равна сумме расхождений.
(5) Фиксированные множители могут быть удалены из сигнального знака.
Например, продолжите исследование и найдите варианты распределения случайной переменной X — количества белых шаров. Давайте построим вычислительный стол:.
Получено: d(x) = 10,9375-3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Явная случайная величина x = стандартное отклонение x (СКО)I.>это квадратный корень из вариации: $ \ mathrm< \sigma(X)=\sqrt> СКО описывает степень отклонения случайной величины от среднего значения.
RMS 1) Размерность RMS равна свойству случайной величины. 2) RMS может быть любым неотрицательным действительным числом. 3) RMS для фиксированных размеров равен нулю:.
(4) Фиксированные множители могут быть удалены из среднеквадратичного синуса.
п.5. Правило трёх сигм
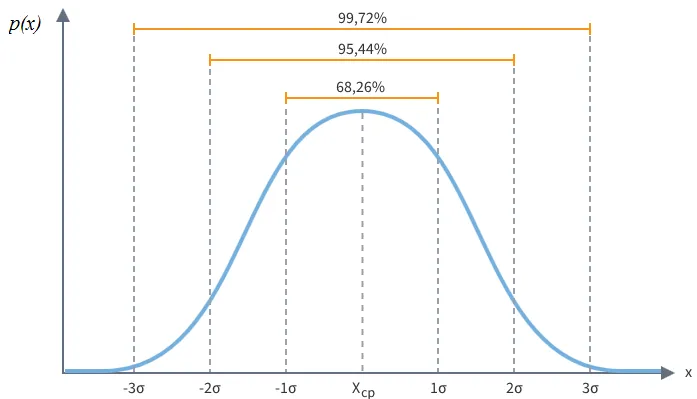
Большое количество случайных величин, измеряемых в экспериментах (школьных лабораторных работах), имеют так называемое нормальное распределение. В частности, при больших n биномиальное распределение может быть хорошо описано как нормальное распределение с m(x) = np и \(\ mathrm> \). График плотности нормального распределения p(x) выглядит как колокол, с максимумом, соответствующим m(x) = xCP. — Среднее значение измеренной цены. Среднеквадратичное значение s(x) описывает степень отклонения x от среднего значения m(x).
Если величина x имеет нормальное распределение, то в пределах ± с существует 68,26% значений, для которых эта величина претерпевает ± 2 с. Это количество должно быть принято. Вероятность того, что нормально распределенная величина отклонится от среднего значения на три сигмы, составляет 0,28%, т.е. ничтожно мала.
Для значений c1 она велика, и в выборке присутствует перекос. Если цена близка к нулю, то выборка нормальная.
Ключевые особенности дисперсии
Диаспора относится к среднему квадрату расхождения между характерными значениями характерных средних. Для обозначения этого используется простая заглавная латинская буква D.
Чтобы правильно рассчитать вариации, необходимо вычислить разницу между имеющимся числом и средним арифметическим, чтобы результат был возведен в квадрат. В результате получается столько цен, сколько фактических результатов для данного события. Затем остается только сложить все данные и разделить на количество последовательностей. Если максимальное количество результатов равно 5, необходимо разделить его на это число.

Вариации также обладают некоторыми свойствами, которые необходимо знать при решении различных математических задач. Например:.
- при увеличении случайной величины в Х раз, тогда дисперсия увеличится в Х раз;
- дисперсия никогда не бывает меньше нуля и не зависит от сдвига значений в большую или меньшую сторону.
Например, был проведен 21 эксперимент, в результате которых было получено семь различных результатов. Первое, что необходимо сделать, это рассчитать среднее арифметическое. Сумма данных равна 21. Это число нужно разделить на 7. Результат будет равен 3. Затем удаляются три из каждого числа в исходной последовательности. Затем каждое значение возводится в квадрат, и результат суммируется. Если все было сделано правильно, результат будет равен 12. Последний шаг — деление чисел на количество предметов.
Зависимость итога от количества экспериментов
Эксперты говорят, что если вариации рассчитаны правильно, то знаменатель может быть n или n -1, одно из двух предложенных чисел. Точное количество проведенных экспериментов обозначается символом n. Если общее количество тестов измеряется сотнями, то в знаменателе должно быть только N. Ученые решили провести весьма символическую границу между этими двумя числами, поскольку сегодня она достигает 30. Если количество экспериментов не достигает этого числа, то общее количество должно делиться только на N-1. N.

Множественные свойства математических ожиданий имеют решающее значение для правильного решения проблемы. Для изучения этой проблемы необходимо знать, что такое стандартное отклонение. Для его обозначения используется буква SD, или маленькая греческая «сигма». Стандартное отклонение показывает, насколько сильно цена отклоняется от центральной черты. Если он основан на нахождении желаемого значения, нужно попытаться правильно вычислить квадратный корень из отклонения.
Вы можете непосредственно проверить фактическое значение среднего квадратного корня, построив диаграмму равновесия. Для этого необходимо выполнить несколько простых упражнений. Вам нужно получить половину изображения справа и половину слева (медиану) от операции и попытаться провести вертикальные линии по горизонтальной оси так, чтобы получившиеся фигуры были абсолютно одинаковыми.
Размер отрезка между средним распределением и полученной проекцией на горизонтальную ось чаще всего будет средним квадратическим отклонением.
Актуальность применения медианы и моды
Математики склонны утверждать, что среднее значение — это некая абстрактная величина. Отталкиваясь от конкретного размера каждого варианта, эти цифры прекрасно отражают общее положение, присущее популяции всего подразделения. В некоторых случаях можно заметить, что значения не имеют равенства ни с одним из конкретных вариантов общего варианта.
Пример: среднее число членов одного домохозяйства равно 4,85. Это число было получено в результате расчета соответствующего набора данных. Это число не имеет никакого отношения к конкретному составу конкретной семьи, поскольку не существует числа членов семьи. В этом случае за основу берется среднее значение состава семьи. Фактические варианты сгруппированы рядом с дробными числами.
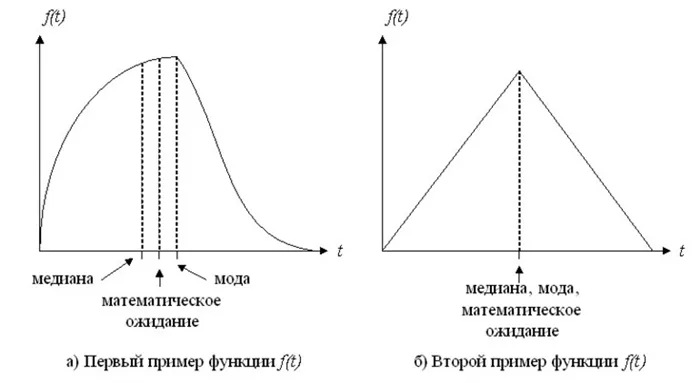
Если целью является определение абстрактного значения, вы можете свободно использовать конкретные необязательные значения, содержащиеся во всех этих значениях. Эти ценности занимают определенное место в классификации индивидуальных ценностей. Медиана и метод являются наиболее распространенными такими значениями. Moda является наиболее распространенным значением и обычно обозначается символом Mo.

Медиана прерывистого столбца всегда определяется путем выявления наибольшей доли мужчин, носящих одинаковый размер обуви. После несложного математического процесса можно понять, что большинство мужчин носят обувь 40-го размера. Это означает, что Мо = 40, мода — это 40 туфель.
Однако, если нужно найти надежную медиану, первое, что нужно сделать, — это найти один из центральных вариантов популяции. В примере исследования вариантов эксперимент со 100 людьми дает основу: 100:2 = 50. Кумулятивная частота используется для определения надежной цены Пятидесятницы. Если следовать кумулятивной частоте, то количество результатов варьируется от 41 до 69. Это означает, что 50-й член ряда равен 40 (ME = 40-й размер обуви).








