Прямая линия может состоять одновременно из многих геометрических фигур, но угол соединения равен нулю. Чтобы избежать грубых математических ошибок, помните, что пунктирная линия отличается от кривой тем, что отдельные участки являются прямыми линиями.
Как определить длину пунктирной линии?
Добавьте длины всех отрезков. Длина полигона ABCDEF, построенного с помощью фишки, равна сумме пяти сторон AB + BC + CD + D + EF.
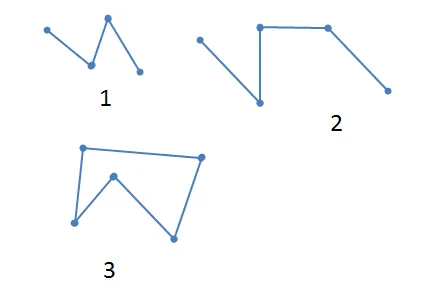
Внимательно посмотрите на картинку и ответьте на вопросы на фишке. 1. какая пунктирная линия сопровождает какое число, состоящее из максимального количества связей? 2.Какая пунктирная линия сопровождает какое число, состоящее из минимального количества связей? 3.Каково количество незамкнутых пунктирных линий? 4. какие прерывистые линии закрыты? 5.Какие линии полигинии имеют три вершины?
СМИ ‘Mathematics-tests.com’ зарегистрировано Федеральной службой по надзору в сфере связи, информационных технологий, медиатехнологий и Роскомнадзора. Свидетельство о регистрации средства массовой информации эл № ФС 77-63677 от 10 ноября 2015 года. название — https: //mathematics-tests.com.
Медиасеть Основатель (соучредитель) издания Mathematics-tests.com: Андреев Г.И., Медиаредактор: Андреев Г.И. Защищено Mathematics-tests.com.
Прямая линия может состоять одновременно из многих геометрических фигур, но угол соединения равен нулю. Чтобы избежать грубых математических ошибок, помните, что пунктирная линия отличается от кривой тем, что отдельные участки являются прямыми линиями.
Ломаная линия
Прерывистая линия — это геометрическая фигура, состоящая из ряда соединенных отрезков, где конец одной части является началом следующей. Однако смежные отрезки (с общими точками) не обязательно должны быть одной и той же прямой линией.
Участки, составляющие многоугольник, называются звеньями, а края этих участков — вершинами многоугольника.
Давайте построим полигам с четырьмя секциями.
Разделы AB, BC, CD и DE являются частями полигама. Точки A, B, C, D и E — это вершины полигама. Сформируйте полигам, называя последовательные буквы на пиках. Например, скажите или напишите Polyline ABCDE или Polyline EDCBA.
Самопересекающаяся ломаная
Закрытые и открытые полигамы могут быть независимыми. Полигоны, линии которых пересекаются сами по себе, — это полигоны, в которых стыки пересекаются между одной или несколькими точками. Например:.
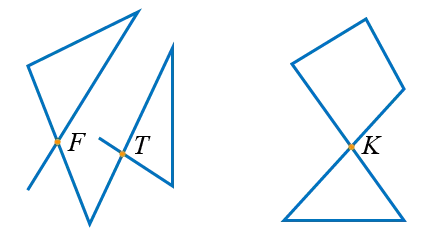
Точки f, t и k — независимые точки, то есть точки, в которых полином пересекается сам с собой.
Длина ломаной
Длина многоугольника равна сумме длин всех его частей. Длина замкнутого многоугольника без независимых разрезов, т.е. длина многоугольника, называется периметром.
Пример 1. Найти длину трехзвенного полигама.
Решение: чтобы найти длину 3-звенного многочлена, сложите длины всех звеньев. Длина многочлена ABCD следующая.
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
ОТВЕТ: длина многоугольника ABCD равна 9 см.
Пример 2: Найдите длину замкнутого многочлена.
Решение: сложите длины всех частей и найдите границу замкнутого многочлена.
AB + BC + CD + DA = 3 см + 5 см + 4 см + 5 см = 17 см.
Дополнительные материалы Уважаемый пользователь, не забывайте оставлять свои комментарии, замечания и предложения. Все материалы контролируются программами защиты от вирусов.
Особенности замкнутых линий
Давайте подробнее рассмотрим составляющие этой геометрической фигуры.
- Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
- Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
- Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
- Ломаная линия может пересекать саму себя.
- Конечные вершины такой фигуры в геометрии принято называть черными точками.
Как уже говорилось выше, этот тип линии эгоцентричен. Наиболее распространенным примером закрытой линии с независимыми разрезами является линия «пять звезд».

Многоугольник как разновидность замкнутой ломаной
Многоугольники — это один из видов геометрических фигур. Точки многоугольника — это его вершины, а отрезки называются сторонами.
- Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
- Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
- Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
- Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
- Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
- Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
- Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.
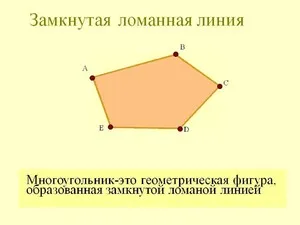
Примерами многоугольников являются четырехугольники, треугольники и пятиугольники. Давайте подробнее рассмотрим отличительные особенности этих форм.
Треугольник — это геометрическая фигура, состоящая не из прямой линии, а из трех точек. Эти точки соединяются в секции и пары.
Четырехугольник в геометрии — это фигура с четырьмя углами и четырьмя сторонами. Существуют все виды четырехугольников — это могут быть таблицы, квадраты, прямоугольники и ромбы.
Две боковые стороны трапеции параллельны и называются основанием. Другие стороны не параллельны. Прямоугольник имеет две противоположные стороны, которые параллельны друг другу.
Особенностью прямоугольника является то, что все его углы правильные. У квадрата все четыре стороны равны. Кроме того, все углы квадрата являются прямыми.
Если все стороны и углы многоугольника равны, он называется нормальным. Такие многоугольники всегда выпуклые.
Аналогично, автору важно подписаться на канал в yandex.zen и вступить в группу Вконтакте!
Если многоугольник расположен по отношению к простой линии на любом уровне, он называется выпуклым. Однако прямая линия содержит одну сторону фигуры и относится к полууровню. Если секция соединяет несмежные вершины, она называется диагональной. Смежные внутренние углы вершины называются внешними углами.
Что такое ломанная: определение, обозначение, элементы, виды, пример задачи
В этой публикации рассматривается, что такое математическая пунктирная линия, как она характеризуется, из каких элементов состоит и какого вида она бывает. В нем также рассматриваются примеры, на которых решаются задачи по этому предмету.
Прерывистая линия — это линия, состоящая из ряда соединенных отрезков, расположенных под разными углами (не 180°).
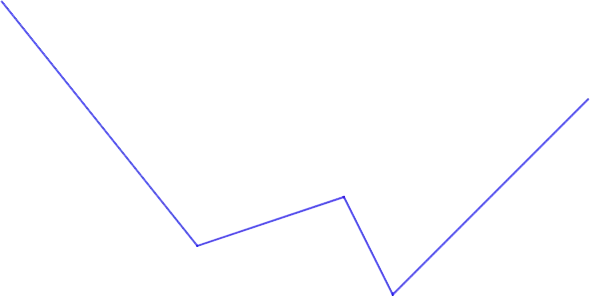
Другими словами, когда длинный участок (в одной или нескольких точках) «разрывается», появляется пунктирная линия.
Элементы пунктирной линии:.
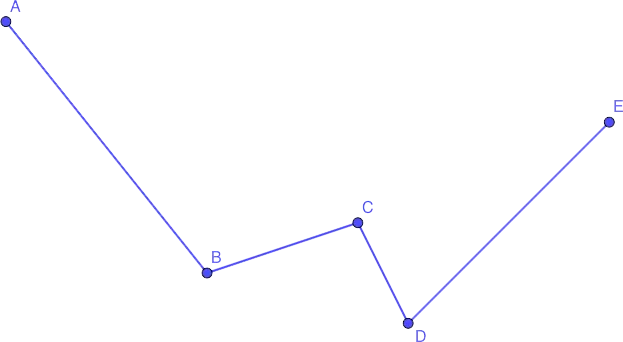
-
Звенья – отрезки, которые образуют ломанную (на рисунке ниже это AB, BC, CD и DE). Если конец одного звена является началом другого, такие звенья называются смежными (AB и BC, BC и СD, CD и DE).
Многоугольник символизируется списком всех вершин. Другими словами, в нашем случае, ABCDE.
Длина многоугольника равна длине всех его частей, т.е. сумма ABCDE = AB + BC + CD + DE.
Виды ломанной
Данная полигима — это многоугольник, состоящий из пяти связок, где длина первой связки составляет 7 см, а каждая последующая связка на 3 см длиннее предыдущей. Найдите общую длину полигиума.
Сначала подсчитайте длину всех звеньев.
- 2 зв. = 7 + 3 = 10 см
- 3 зв. = 10 + 3 = 13 см
- 4 зв. = 13 + 3 = 16 см
- 5 зв. = 16 + 3 = 19 см
Осталось только сложить все эти значения, чтобы получить длину полигама: 7 + 10 + 13 + 16 + 19 =
Этот вариант геометрии можно представить как зигзаг, где последовательные отрезки образуют прямые углы и параллельны друг другу. Зиг — Заги широко используются в повседневной жизни, например, в шитье, декоративном искусстве и бытовых предметах.
Чем ломаная линия отличается от прямой
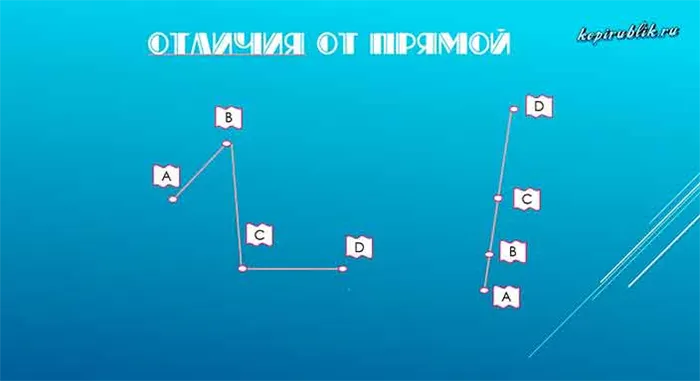
Дизайн делает это очевидным. Уникальной особенностью пунктирных линий является то, что не существует углов, равных 180 градусам. В остальном формы одинаковы и имеют схожие характеристики, например, длину.
Примеры ломаных линий в быту
Чтобы лучше понять теорию, целесообразно рассмотреть примеры прерывистых линий из жизни и практики.
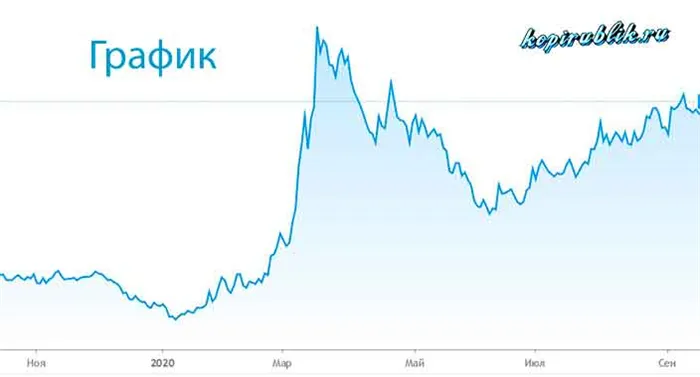
Пунктирная линия — это график фондового рынка. Это может выглядеть как кривая, поскольку части диаграммы очень малы, но при ближайшем рассмотрении это не так.
Фасад дома, в переводе на «язык геометрии», выглядит как замкнутая пунктирная линия.

Древнеегипетские пирамиды были треугольными, это одна из самых популярных пунктирных линий.
Данная полигима — это многоугольник, состоящий из пяти связок, где длина первой связки составляет 7 см, а каждая последующая связка на 3 см длиннее предыдущей. Найдите общую длину полигиума.
Особенности построения многоугольников
В данном случае речь идет о геометрической форме, которая отличается от общего количества суставов и углов. Последняя может быть образована только множеством стыков в замкнутой полилинии, сходящихся в одной точке. Соответствующие связи логически также можно назвать ребрами многоугольника. Общая точка между двумя частями называется вершиной. Стоит учесть, что количество сторон или стыков такой фигуры в точности соответствует количеству углов. Замкнутая полилиния с тремя сегментами образует треугольник.
Абсолютно все многоугольники обладают одинаковыми свойствами. Меньшая форма имеет только три стороны. Однако близлежащие треугольники могут образовывать совершенно новые фигуры. Если существующие вершины изучаемого многоугольника являются своего рода дополнением сторон, то они всегда называются смежными.
Если многоугольник расположен по отношению к простой линии на любом уровне, он называется выпуклым. Однако прямая линия содержит одну сторону фигуры и относится к полууровню. Если секция соединяет несмежные вершины, она называется диагональной. Смежные внутренние углы вершины называются внешними углами.
Обратите внимание, что если все углы и ребра многоугольника равны друг другу, то они являются нормальными отрезками. Каждая геометрическая форма имеет определенные параметры. Алгебраические треугольники обычно относятся к обычным плоским фигурам, состоящим из трех точек, которые не расположены на прямой линии. Для их соединения используются общие детали. Точки являются вершинами треугольника. В этой диаграмме всего три угла. Эксперты выделяют шесть типов треугольников.
- Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
- Равносторонние. Абсолютно все стороны обладают идентичной длиной.
- Специфические остроугольные. Сформированные углы имеют острую форму.
- Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
- Тупоугольные. Фигура обладает одним тупым углом.
- Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.
Четырехсторонний — это структура с четырьмя сторонами и четырьмя гранями. Существуют определенные нюансы использования таких геометрий.
Ключевые нюансы
Есть две прямые равной толщины, SWT и SFT, соединяющие свободные концы прямой ST. Результат — пунктирная линия. Кривая SFT называется внутренней полилинией, а SWT — внешней полилинией. В качестве примера целесообразно рассмотреть фигуру, которая удовлетворяет математической теореме о том, что внешняя кривая превышает внутреннюю.
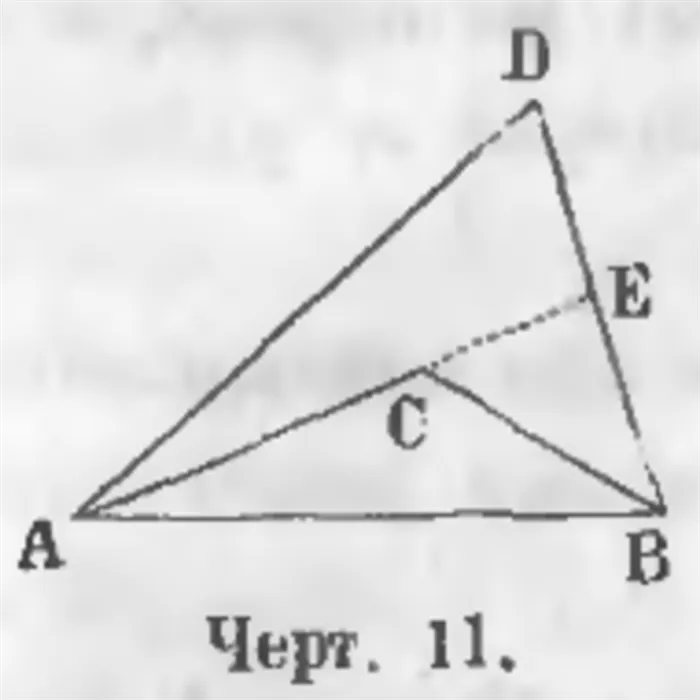
С точки зрения проблемы, были заданы два полигона — внутренний SFT и внешний SWT. Необходимо доказать, что SWT больше, чем SFT. Чтобы решить эту проблему, продолжите линию SF и пересеките отрезок WT в точке E. Линия SWE как мультилиния намного больше, чем линия SE. Пунктирная линия FET больше прямой линии FT. Суммирование всех этих неравенств дает SW + WE + FE + ET> SF + FE + FT.
Чтобы получить достоверный результат, вычтите SE из обеих частей неравенства.
Вторую теорему также необходимо учитывать, когда сумма пересекающихся кривых линий больше, чем не пересекающихся. В данных условиях были получены обычные запутанные и прерывистые линии HLK и HRK, с частями HR, LK и скрещивания. Решение заключается в следующем. Неравенство отрезков происходит от того, что полигирус HEL намного больше линии HL, но координаты Ker превышают KR.
Это также поможет научиться находить две общие линейные меры с помощью линейки. Это правило необходимо в начальной школе. Чтобы найти неизвестную общую меру, нужно продублировать наименьшую минимальную строку, затем наименьший остаток и первый остаток первого остатка. Все эти операции повторяются ровно до тех пор, пока последний остаток не будет соответствовать второй от последней произведенной энергии. Измерение линии всегда означает, что ученик должен найти причину для других длин. Принятое значение называется длиной линии, которая может быть выражена только в единицах.
Изучение прерывистых линий очень важно, потому что они окружают людей повсюду. Это оригинальные направления, подходы и пересекающиеся прямые линии.
Пунктирная линия — это график фондового рынка. Это может выглядеть как кривая, поскольку части диаграммы очень малы, но при ближайшем рассмотрении это не так.
Длина ломаной
Длина полигама равна сумме длин отрезков.
Теорема о длине полигама может быть доказана.
Длина полигама больше расстояния между ребрами.
Пример:
Сечения полигама EFMO равны: ef = 1 см, fm = 4 см, mo = 2 см. Равно ли сечение ef: a) 0,5 см, b) 8 см;
2. ef = 1 см, fm = 4 см, mo = 2 см; (рис. 2.45)
3. сечение ЭО может быть равно a) 0,5 см, b) 8 см.
На рис. 2.45 отсутствуют секции EO.
4. начертите разрез (конструкцию) УО (рис. 2.46).
Связь между заданным полигамом EFMO и сечением EO определяется теоремой о длине полигама.
5. длина полигамы EFMO не должна быть меньше длины сегмента EO (1, 2, 4, Теорема 3).
6. длина сломанного EFMO равна 7 см (1, 2).
7. длина участка УО не должна превышать 7 см (4, 5).
8. длина участка EFMO может быть 0,5 см, но не может быть равна 8 см (1, 2, 7).
Эта лекция взята со страницы с полным текстом урока «Математика».
См. также дополнительные лекции по предмету математика.
Отправляйте задания в любое время дня и ночи.
Официальный сайт Брилиджоно Банаталия Валерия Эванта Екатеринбургского государственного педагогического института.
Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.
Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.
При копировании материалов ссылка на сайт Natalibrilenova.ru обязательна.








