Теперь поговорим о наиболее распространенных логарифмах. У них даже есть названия: десятичный логарифм и натуральный логарифм. Давайте перейдем к делу.
7. Логарифмы и логарифмическая функция
Рассмотрим уравнение, в котором возникает вопрос: до какой степени нужно преобразовать 2 в 8? Ответьте на этот вопрос, используя логарифм, равный 3. … Сложный; гм, этому не учат бесплатно в средней школе, Дж. — На сколько нужно увеличить ‘e’, чтобы получить 1? -Какая сила 10, чтобы получить 1/100? Действительно, на сколько нужно увеличить «a», чтобы получить «b»?
Логарифм числа по основанию: — является мощностью ‘pe’. Здесь «a» нужно увеличить, чтобы получить «b». Источник производной базового логарифмического тождества:. … Идентичность — это такое непоколебимое равенство:) сам символизм читается как логарифм «b», основанный на «a», и ясно, что логарифм определен только для положительного «b»: — по той причине, что фактическое положительное «a» «pe». -положительный. Логарифм с основанием ’10’ называется десятичным логарифмом и для краткости обозначается символом Логарифм по основанию ‘e’ называется натуральным логарифмом и обозначается символом. В высшей математике используются натуральные логарифмы, которые более подробно будут рассмотрены позже.
Свойства логарифмов
Как и в случае с силами/корнями, сосредоточьтесь только на тех свойствах, которые действительно важны, а не проверяйте все свойства. Переход к новой базе данных. При необходимости вы можете выбрать новую базу данных (из доступных вариантов:). Пример. Однако гораздо чаще встречаются следующие типы особых случаев. Например:. Конечно, формула работает и в обратном направлении. Это полезно, когда вы хотите удалить знаменатель. Если применяется следующее (как слева направо, так и справа налево): .
Например:. Обратите внимание, что эти действия возможны только при логарифмеТо же самое. основа, которую не следует путать с «аналогичной» ситуацией: or. Однако в последнем случае возможно следующее Следующий. Для любого действительного числа:.
Пример: — и это волшебно! В конце концов, избавиться от 50 градусов — это здорово! Обратное правило также популярно, особенно если нужно сделать другие упрощения: вышеприведенное правило можно распространить на отрицательные значения b, но нужно добавить модуль: — и это волшебство!
, если таковые имеются. Далее приводится пример. -и полученный логарифм также определен для отрицательного «x», так что эквивалентность соблюдена. Однако это преобразование не равно: и здесь необходимо всегда уточнять. Для других значений раздел не нужен: — потому что и начальный логарифм, и принимающий логарифм определены только для положительных значений ‘x’.
Логарифмирование и потенцирование
Логарифм — это преобразование числа или уравнения в логарифмической шкале, или, проще говоря, «плавающий» логарифм. Это особенно полезно для астрономических или небольших чисел, особенно для продуктов. Поэтому, если вы хотите «подцепить» логарифм для упрощения числа, рекомендуется использовать десятичный логарифм. -преобразовывать другие числа по той же шкале (с логарифмом, заканчивающимся на 10), гораздо удобнее по цене. Логарифмы необходимы для решения некоторых уравнений.
Для решения этого уравнения относительно логарифма «x» «мы висим» обычно используется натуральный логарифм.
И «любительская» проверка: около 80, это то, что мы должны были контролировать. Согласно логарифму, здесь можно смело логарифмировать, так как обе части уравнения (функции) определяются произвольным значением ‘x’ и являются положительными, поэтому нужно обратить внимание на их знаки. Однако здесь необходимо добавить модуль, так как обе части функции могут быть меньше нуля. Однако мы потеряли ценность, и эта энергия по-прежнему неоднородна (почему?).. Однако это не является препятствием для решения конкретной проблемы. Мы находим производные, которые даже вкладчики могут игнорировать. Да, почему логарифмический? Для упрощения правильно:.
Усиление — это обратное действие, «освобождение» логарифмов. Предположим, молодой физик много развлекается вычислениями в логарифмической шкале с десятичными точками и хочет отменить результаты. Нет проблем: используйте свойства силы, логарифма и основного логарифмического тождества. Усиление «упаковывает» логарифм справа: используется для явного выражения функции в «упаковке».
и просто удаляет логарифм и числитель одновременно.
Такие действия выполняются при решении определенных дифференциальных уравнений
Второй тип показывает, что основание и аргумент логарифма можно поменять местами, но все уравнение является «обратным». То есть, логарифм находится в знаменателе.
Логарифмы и их свойства
Обычно определение логарифма очень сложное и запутанное. Мы стараемся сделать все очень просто и понятно.
Чтобы понять, что такое логарифм, давайте рассмотрим пример.
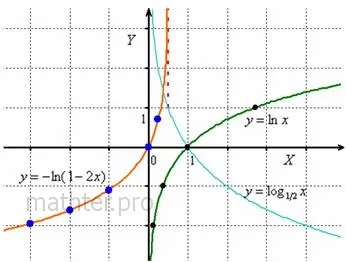
Все знают, что такое степени числа (если нет, то вы здесь). В таблице показаны различные степени 2. Глядя на таблицу, видно, например, что число 32 — это пятая сила двух, то есть только два — это умножение в пять раз.
Теперь, с помощью этой таблицы, мы можем ввести понятие логарифмов.
Логарифм числа 32 по основанию 2 (ǫ(log_(32)ǫ)) — это сила 2, равная 32. Из таблицы видно, что мы должны возвести 2 в пятую степень. Следовательно, наш логарифм равен 5.
Аналогично, глядя на таблицу, получаем: логарифм по основанию 2.
Разумеется, логарифм имеет не только основание 2, но и различные основания, каждое из которых превышает 0 и 1 соответственно. Мы можем даже создавать таблицы с разными числами. Но, конечно, со временем вы делаете это мысленно.
Теперь дадим общее определение логарифмов.
Логарифм положительного числового значения ɛ (b \) на основе положительного числового значения ɛ (a \) — это сила ɛ (c), на которую нужно уменьшить ɛ (a \), чтобы получить ɛ (b \).
Внимание. Поначалу принято путать, что такое основание и что находится под логарифмом (аргументом). Логарифмы — это функции, которые всегда зависят от двух переменных. Чтобы избежать путаницы, помните, что определение логарифма — это мощность аргумента, принимаемого за основание.
Но, конечно, часто приходится сталкиваться с логарифмами, которые не так просты, как оба примера, и очень часто оказывается, что логарифм нельзя вычислить в уме. Действительно, что бы вы сказали о его логарифме 5 по основанию 2:.
Как вы считаете? Использование калькуляторов. Вы обнаружите, что такой логарифм равен ненулевому числу.
Или логарифм 6 по основанию 4:.
На экзаменах и соревнованиях принято оставлять эти логарифмы в виде логарифмов, так как в курсе математики нельзя пользоваться калькулятором — не считать же их!
Однако иногда вы можете столкнуться с задачей, в которой вам нужно оценить приблизительную цену лорума — это довольно просто! Например, благодаря логарифмическим вычислениям (log_(6)™). Вы должны найти левую и правую 6-ки, которые ближе всего к логарифму, который вы можете вычислить. Другими словами, вам нужно найти силу 4, которая ближе всего к 6.
$ log_(4)™ lt log_(6)™ lt log_(16); $ 1 \ lt log_(6)™ lt 2. $
Следовательно, Ǿ (log_(6)Ǿ) лежит между 1 и 2.
Как посчитать логарифм
Как это произошло; это вытекает из определения экспоненциальной функции. Экспоненциальная функция не может быть ⌘(0 \). И основание не может быть равно \(1 \). Это потому, что логарифм не имеет смысла — ведь \(1 \) это \(1 \).
При этих ограничениях логарифмы существуют.
Позже мы увидим, что различные логарифмические уравнения и решения неравенств могут быть полезны для ERD.
Обратите внимание, что сам логарифм может иметь любое возможное значение. Это степень и может быть любой степени — отрицательной, разумной, неразумной и т.д.
Давайте теперь проанализируем общий алгоритм вычисления логарифма.
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень \(x\) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- \(x\) и будет искомым значением логарифма.
Давайте проанализируем это на примере.
Пример 1. \(3 \): вычислите логарифмическое Ј(9 \) на основе Ј(log_(9)Ј).
- Сначала представим аргумент и основание в виде степени тройки: $ 3=3^1, \qquad 9=3^2;$
- Теперь надо разобраться в какую степень \(x\) нужно возвести \(3^1\), чтобы получить \(3^2\) $ (3^1)^x=3^2, $ $ 3^=3^2, $ $ 1*x=2,$ $ x=2.$
- Вот мы и решили: $log_(9)=2.$
Пример 2. base\(5 \): вычислите логарифм от\(Јfrac)Ј на основе\(log _(Јfrac)Ј.
- Представим аргумент и основание в виде степени пятерки: $ 5=5^1, \qquad \frac=\frac=5^;$
- В какую степень \(x\) надо возвести \(5^1\), чтобы получить \(5^\): $ (5^1)^x=5^, $ $ 5^=5^,$ $1*x=-3,$ $x=-3.$
- Получили ответ: $ log_(\frac)=-3.$
Пример 3. Основание \(64 \): вычислите логарифм \(4 \) с помощью \(log _(4)\).
- Представим аргумент и основание в виде степени двойки: $ 64=2^6, \qquad 4=2^2;$
- В какую степень \(x\) надо возвести \(2^6\), чтобы получить \(2^\): $ (2^6)^x=2^, $ $ 2^=2^,$ $6*x=2,$ $x=\frac=\frac.$
- Получили ответ: $ log_(4)=\frac.$
Пример 4. Основание \(8 \): вычислите логарифм \(1 \) в \(log_(1)\).
- Представим аргумент и основание в виде степени двойки: $ 8=2^3 \qquad 1=2^0;$
- В какую степень \(x\) надо возвести \(2^3\), чтобы получить \(2^\): $ (2^3)^x=2^, $ $ 2^=2^,$ $3*x=0,$ $x=\frac=0.$
- Получили ответ: $ log_(1)=0.$
Пример 5. Основание \(5 \): вычислите логарифм \(15 \) с помощью \(log_(15)\).
- Представим аргумент и основание в виде степени пятерки: $ 5=5^1 \qquad 15=. ;$ \(15\) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть: $ log_(15).$
Как понять, что число ĩ(a \) не является мощностью другого числа ĩ(b \). Это очень просто — достаточно проанализировать первый фактор.
Мы проанализировали \(16 \) как произведение четырех двух. Это означает, что Lo_16 \) является степенью двойки.
Анализ \(48 \) с помощью первого фактора показывает, что есть два множителя \(2 \) и \(3 \). Следовательно, ⌘(48 \) не является степенью.
Теперь поговорим о наиболее распространенных логарифмах. У них даже есть названия: десятичный логарифм и натуральный логарифм. Давайте перейдем к делу.
Десятичный логарифм
На самом деле, все очень просто. Десятичный логарифм — это обычный логарифм, основанный на 10. \ Он называется ɛ(lg(a)ɛ).
Натуральный логарифм — это логарифм по основанию ዄ(e \)ዅ. \Это обозначается ᥉(ln(x)᥉). Что такое \(e \)? Это экспонента и есть число, равное примерно ܘ(2,71828281828459 … (\)), что является числом, равным примерно. Это число, как известно, используется во многих математических методах. Помните, что специальное название — натуральный логарифм — появилось потому, что логарифмы, основанные на \(e \), являются обычными.
Физические и десятичные числа обладают теми же свойствами и следуют тем же правилам, что и обычные логарифмы.
Логарифмы обладают различными свойствами, которые можно преобразовывать и вычислять. В дополнение к этим качествам, логарифмы не могут быть выполнены.
Значение логарифма соответствует экспоненте конкретного основания, равной положительному числу ‘b’ основания ‘A’.
Вынесение показателя степени из логарифма
Теперь давайте немного усложним ситуацию. Что произойдет, если основание или аргумент логарифма имеет класс? Затем эту степень экспоненты можно получить над логарифмом, используя следующие правила.
Вы видите, что последнее правило вытекает из первых двух. Однако лучше помнить, что — в некоторых случаях — это значительно уменьшает сумму расчета.
Конечно, все эти правила имеют смысл, если логарифм выполняется: a> 0, a≠1, x> 0., число можно поставить перед знаком логарифма. Это требуется чаще всего.
Вопрос. Найдите значение выражения: log7 49 6.
Удалите оценку аргумента в первом типе: log7 49 6 = 6-лог.7 49 = 6-2 = 12
Задача. Найдите значение выражения:.
Подпись.
Обратите внимание, что знаменатель — логарифм, основание и аргумент которого — точные силы: 16 = 2 4? 49 = 7 2. Тогда имеем:.
Подпись.
Я думаю, что последний пример нуждается в пояснении. Куда исчезли рогальцы? До последней минуты работайте только со знаменателем. Представьте логарифмическую основу и аргумент в терминах мощности и уберите объясняющего — в «трех историях» всего несколько дробей.
Далее рассмотрите основные дроби. Числитель и знаменатель — одно и то же число2 7. с журнала.2 7≠0, фракция может быть уменьшена до точки бифуркации. Он остается в знаменателе. Согласно правилам арифметики, четыре можно перенести в числитель, что и было сделано. Результат — ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркнул, что они работают только в том случае, если основания одинаковы. Но что происходит, если основания разные? Что произойдет, если они не являются точной силой одного и того же числа?
Вам на помощь приходит тип конверсии на новую базу. Сформулируйте их в виде теорем.
Используйте логарифм логарифмаa БЬЮТС. Тогда для каждого значения c, при c> 0 и c≠1, равенство верно.
Подпись.
В частности, если задать c = x, то получится
Подпись.
Второй тип показывает, что основание и аргумент логарифма можно поменять местами, но все уравнение является «обратным». То есть, логарифм находится в знаменателе.
Эти типы редко встречаются в обычных числовых выражениях. Только при решении логарифмических уравнений и неравенств можно оценить, насколько они полезны.
Однако существует несколько проблем, которые можно решить только путем изменения новой основы. Давайте рассмотрим некоторые из них:.
Вопрос. Найдите значение выражения: log5 16 кал.2 25.
Обратите внимание, что оба логарифма имеют в аргументах точную мощность. Удалить экспонента: журнал.5 16 = дневник5 2 4 = 4log5 2; журнал.2 25 = журнал2 5 2 = 2log2 5;
Теперь «переверните» второй логарифм.
![]()
Подпись.
Поскольку произведение не зависит от счетчика множителей, мы безопасно перемножили четыре и два, прежде чем обратиться к логарифму.
Вопрос. Найдите значение выражения: log9 100 -LG 3.
Основание и аргумент первого логарифма — это точная оценка. Запишите и удалите экспонент:.
![]()
Подпись.
Далее перейдем к новому основанию и извлечем десятичный логарифм.
![]()
Подпись.
Основное логарифмическое тождество
Часто, когда мы решаем какое-либо число, мы хотим выразить его в виде логарифма по определенному основанию. В этом случае нам помогает тип: число n.
В первом случае число n является экспонентой степени аргумента. Число n может быть абсолютно произвольным, просто потому, что это логарифмическая цена.
Второй мужчина — это фактически перефразированное определение. Она называется :.
В самом деле, что произойдет, если вы увеличите B на силу так, что эта сила B придаст A силу A? Правильно: вы получите именно это число. Еще раз внимательно прочитайте этот абзац — многие люди придерживаются его.
Как и при любом переходе на новую основу, базовый логарифмический идентификатор может быть единственно возможным решением.
Задача. Найдите значение выражения:.
Подпись.
Обратите внимание на журнал.25 64 = журнал5 Просто удалите квадрат из основания 8-лога и аргумента. Принимая во внимание правила распространения силы с тем же основанием, мы имеем
![]()
Подпись.
Если кто-то не знает, это было настоящей проблемой из-за использования:)
Конечно, все эти правила имеют смысл, если логарифм выполняется: a> 0, a≠1, x> 0., число можно поставить перед знаком логарифма. Это требуется чаще всего.
Зачем нужны логарифмы в жизни
В повседневной жизни мы сталкиваемся с гораздо большим количеством логарифмов, чем кажется на первый взгляд. Ниже приведен пример использования.
Децибелы, которые измеряют относительную интенсивность любого данного звука, рассчитываются с помощью цифры после запятой. Это связано с тем, что он измеряется минимальным пределом интенсивности, который может быть услышан соответствующим лицом. Например, громкость звука в 20 децибел означает, что он в 100 раз сильнее тихого звука, а 30 децибел — в 1000 раз.
В химии активность ионов водорода также измеряется в логарифмической шкале.
Выдержка и диафрагма также изменяются. Это означает, что каждое новое значение выше или ниже предыдущего фактора.
В ракетостроении уравнение Циолковского используется для расчета скорости ракеты. Это уравнение основано на логарифмической зависимости между массами ракеты с топливом и без топлива.
Логарифмы в природе
Большинство логарифмов встречаются в природе в виде логарифмических спиралей. Математический вид спирали выглядит следующим образом
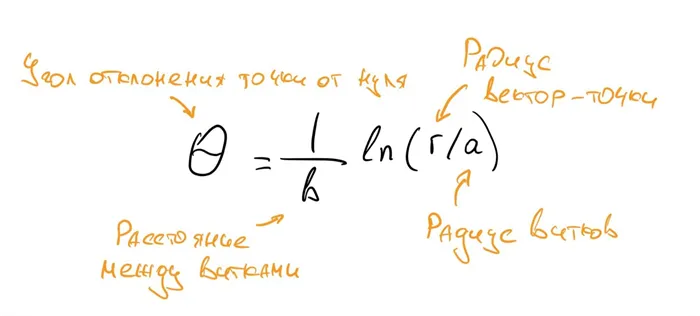
Если вы хотите построить график этого уравнения следующим образом:.
Логарифмически-подобные спирали в математике.
А вот по сути логарифмическая спираль — ракушка, подсолнух, бутон. Еще одна интересная проблема — фракталы — связана с капустой, но о них мы еще поговорим.



Даже рожки рога следуют логарифмической спирали: у









