Последнее свойство очень часто используется в сложных логарифмических уравнениях и неравенствах. О ней часто забывают, но ее нужно помнить, как и всех остальных.
Тема 13. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. Теория.Ключевые методы решения задач.Упражнения. материал для подготовки к егэ (гиа) по алгебре (11 класс) по теме
Актуальной задачей сегодня является подготовка к Единому государственному экзамену по математике (ЕГЭ) и вступительному экзамену в вуз по математике в форме как письменного экзамена, так и викторины.
Имея многолетний положительный опыт подготовки студентов и абитуриентов к различным формам экзаменов по математике, считаю целесообразным поделиться своими разработками с теми, кто в них заинтересован.
Тема 13 «Логарифмические уравнения» содержит теоретическую информацию, структурированный набор основных методов решения стандартных задач и подробный анализ решений. За каждым методом следуют упражнения, включающие ответы для закрепления изученного материала.
Материал полезен для использования учителями элективных общеобразовательных и элективных математических курсов при подготовке к Единому государственному экзамену, а также кандидатами для поступления в высшие учебные заведения.
Скачать:
Тема 13.Логарифмические уравнения и неравенства.
Логарифмическое уравнение — это уравнение, в котором неизвестное число находится ниже или в основании логарифма.
Логарифм числа с основанием — это экспонента, основание которой должно быть возведено в степень. Другими словами, радикс приобретается и наоборот.
- .
- — запись числа через логарифм.
- — основное логарифмическое тождество.
- — формула перехода к логарифму по основанию
- .
Основные методы решения логарифмических уравнений.
I. Согласно определению логарифма.
Это самая простая форма решения уравнений.
Решение. Согласно определению логарифма: берем.
Суть этого метода заключается в следующем. Используйте формулу для придания уравнению следующего вида
Решение. ODE (диапазон допустимых значений переменных):. Преобразуйте исходное уравнение.
Не удовлетворяет ЗФЗ и удовлетворяет ЗФЗ.
Решение. ОДЗ:
Найдите связь между основаниями логарифмов. Используя полученное кубическое разностное уравнение.
Цена удовлетворяет FDZ, но не удовлетворяет FDZ.
III. как ввести неизвестное (замена).
Замена обычно происходит после определенного преобразования конкретного уравнения.
Решение. В первой сумме ODE используйте полученное уравнение и перейдите к основанию 25. То есть, умножив обе части уравнения ввести новую переменную, которая символизирует Имеется новое квадратное уравнение с новыми неизвестными.
. Решив ее, мы находим, используя символику, что получаем
Найденная нами цена удовлетворяет FDZ.
Решение. ОДЗ
Найденное значение удовлетворяет уравнению.
IV. метод уменьшения базы.
Обычно в примере указывается, на какую базу нужно переехать. Часто метод сокращения в базе «работает» с методом замещения.
Разрешение. ODE:. Переход к двоичной системе с помощью формулы
Цены, которые мы нашли, соответствуют EFA.
Решение. ORD: Используйте формулу для перехода к двоичному числу.
Затем исходное уравнение переписывается в виде
. и получаем уравнение, выразив его в терминах
Найденная нами цена удовлетворяет FDZ.
Уравнения с неизвестными величинами как в дне, так и в показателе решаются путем записи левой и правой частей в нескольких днах. В зависимости от типа уравнения выбирается логарифмическое дно.
Решение. Для этой задачи мы рекомендуем записать обе части уравнения по основанию 10, так как в условии уже содержится логарифм десятичной дроби.
Далее вводятся новые переменные. Затем уравнение переписывается в виде (далее)
Решение. ECD: префикс обеих частей уравнения к.
Найденные нами цены удовлетворяют ОДВ.
По теме: методические разработки, презентации и конспекты
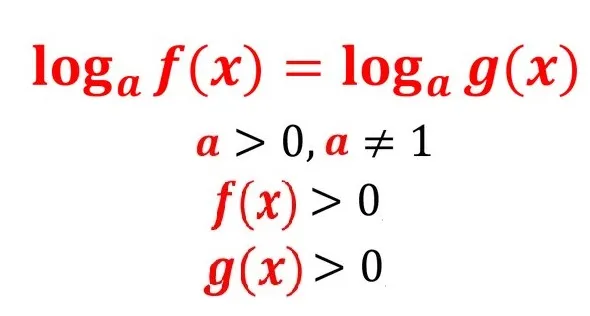
Тема 1: Рациональное уравнение. Гипотеза. Основной метод решения проблем.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.

Тема 2: Теория уравновешенных уравнений. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.
Тема 3: Определяющие уравнения и применение теоремы о ступенях. Гипотеза. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.
Тема 9: Соответствующие уравнения. Гипотезы. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.
Выпуск 10, 11. научное уравнение стали. Научная халатность. Теория. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.

Тема 12.Преобразование и вычисление логарифмических представлений. Теория. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.
Тема 14.Логарифмические неравенства. Теория. Основные методы решения проблем. Упражнения.
Коллеги! Смежным проектом на сегодняшний день является качественная подготовка учащихся к Единому государственному экзамену по математике (ЕГЭ), а также кандидатов на поступление.
Это не самые простые свойства, о которых мы писали в начале урока, и поэтому именно их мы будем использовать сейчас для решения задачи.
Как решать уравнения с логарифмами: 2 способа с примерами
Логарифмические уравнения можно решать несколькими способами. В большинстве случаев в школах учат решать логарифмические уравнения, используя определение логарифма. Это означает, что уравнение может иметь следующий вид Вспоминая определение логарифма, мы имеем следующее Поэтому существуют простые уравнения, которые можно легко решить.
При решении логарифмических уравнений важно помнить о диапазоне логарифма, поскольку аргумент f (x) должен быть больше нуля. Поэтому после решения логарифмического уравнения всегда нужно проверять.
Давайте посмотрим, как это работает на примере.
Используя определение логарифма, мы видим, что
Теперь у нас есть простое уравнение, которое легко решить.
Давайте проверим это. Замените x в исходном уравнении: 32=9, поэтому последнее уравнение верно. Следовательно, x=3 является корнем уравнения.
Основной недостаток этого метода решения логарифмических уравнений заключается в том, что многие дети путаются в том, что именно нужно возводить в степень. То есть, при преобразовании логарифмаaЕсли f(x) = b, многие люди делают b степенью a, а не b. Эта досадная ошибка может лишить ЕГЭ ценных баллов.
Поэтому вот еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, необходимо правую и левую части уравнения привести к форме с одинаковым основанием логарифма. Это происходит следующим образом.
После приведения уравнения к такому виду логарифм можно «убрать» и решить простое уравнение. Давайте рассмотрим это на примере.
Давайте снова решим то же уравнение. Однако сделайте следующее. В левой части находится логарифм, основанный на 2. Поэтому нам нужно преобразовать логарифм так, чтобы в правой части логарифма также стоял логарифм, основанный на 2.
Для этого вспомните свойства логарифма. Первое свойство, которое нам здесь необходимо, — это логарифмическая единица. Помните: то есть, в нашем случае: возьмем правую часть уравнения и начнем ее преобразовывать: затем нам нужно превратить оба выражения в логарифмические. Для этого вспомним еще одно свойство логарифмов.
В данном случае это свойство позволяет нам Правая часть уравнения была преобразована в требуемый формат и получена. Поскольку левая и правая части уравнения имеют логарифмы с одинаковым основанием, их можно удалить. В результате получается следующее уравнение
Да, в этом методе больше шагов, чем в решении логарифмического определения. Однако все шаги логичны и последовательны, поэтому вероятность ошибок меньше. Кроме того, этот метод предоставляет больше возможностей для решения более сложных логарифмических уравнений.
Давайте рассмотрим другой пример. Как и в предыдущем примере, применяется логарифмическое свойство, и правая часть уравнения преобразуется следующим образом После преобразования правой части уравнение принимает вид Теперь вы можете удалить следующие формы логарифм и следующее. Вспомните свойства сил.
Пример решения логарифмического уравнения с разными основаниями
Выше мы решили логарифмическое уравнение с логарифмами с одинаковым основанием. Но что произойдет, если логарифмы имеют разные основания? Например.
Правильно, правый и левый логарифмы должны быть приведены к одному и тому же основанию!
Давайте теперь проанализируем пример. Преобразуем правую часть уравнения.
Мы видим, что 1/3 =3-1. Мы также знаем свойства логарифмов, т.е. вычитание экспоненты из логарифма. Применяя эти знания, мы получаем Однако, пока в правой части уравнения перед логарифмом стоит знак «- вы не имеете права удалять его. Вы должны добавить знак «-» к логарифмическому уравнению. Для этого используйте другое свойство логарифма.
Далее, возьмите это. Теперь у вас есть логарифмы с одинаковым радиксом в правой и левой частях уравнения, и вы можете их удалить. Проверьте: если преобразовать правую часть, используя свойство логарифма, то получится x=4 — уравнение с корнями.
Пример решения логарифмического уравнения с переменными основаниями
Выше мы рассмотрели пример решения логарифмического уравнения с фиксированным основанием. То есть, для конкретного значения -2, 3, ½… Однако основание логарифма может включать x, и такое основание называется переменным. Например, дневникЛетучие мыши.+1(x 2 +5x-5) = 2. Мы видим, что логарифмическим основанием этого уравнения является x +1. Как же решить это уравнение? Мы решаем ее, используя те же принципы, что и раньше. Другими словами, преобразуйте уравнение так, чтобы левый и правый лоралиан имели одинаковое основание. Преобразуйте правую часть уравнения. Теперь логарифмы в правой части уравнения имеют то же основание, что и логарифмы в левой части. Теперь вы можете удалить логаримы.. Назовите все требования к логарифмам.
1.Поэтому аргумент логарифма должен быть больше нуля.
2.Основание логарифма должно быть больше нуля и равно единице, поэтому следует, что
Объедините все требования в вашей системе.
Эта система требований может быть упрощена. Убедитесь, что x 2 + 5x-5 больше нуля, равно (x + 1)2 и больше нуля. Поэтому требование x 2 +5x-5> 0 выполняется автоматически и не требует решения. Затем система сокращается следующим образом Система переписана. Таким образом, система имеет вид Затем уравнение решается. Общая площадь находится в правой части. -1, что не равно 0 больше, чем 1. Следовательно, x = 2 является корнем уравнения.
Убедитесь, что вы можете проверить, заменив x = 2 на исходное уравнение.
Поскольку 3 2 = 9, последнее уравнение верно.
Еще раз отметим, что при решении логарифмических уравнений необходимо учитывать диапазон допустимых значений. Поэтому основание логарифма должно быть больше нуля и равно единице. И его настрой должен быть позитивным. Другими словами, она больше нуля.
Два очевидных следствия определения логарифма
Действительно, если вы получите число A в первой степени, вы получите то же самое число, возведите его в нулевую степень, и вы получите единицу.
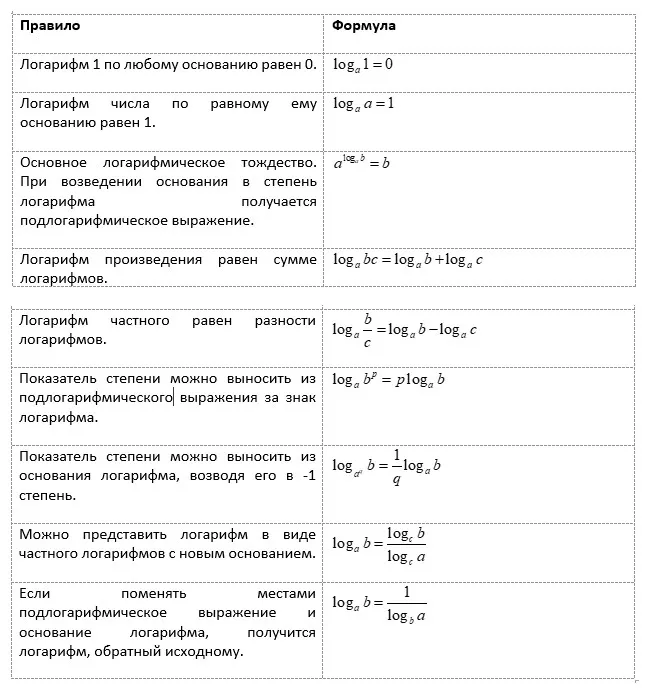
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества.
| ( основное свойство логарифмов ), |
| ( основное свойство логарифмов ), |
| ( формула перехода к новому основанию логарифмов ), |
Степень можно выносить за знак логарифма
Опять же, вы хотите быть точными. Рассмотрим следующий пример.
Log a (f (x))2 = 2 log a f (x)
Левая часть уравнения однозначно определена для всех значений f (x), кроме нуля. Правая часть применима только для f(x) > 0! Удалив степень из логарифма, FDZ снова ограничивается. Обратная процедура приводит к расширению поля допустимых значений. Все эти замечания относятся к каждому из балансов, а также к классу 2.
Логарифм произведения и логарифм частного
Log a b c = log a b — log a c (a> 0, a≠1, b> 0, c> 0)
Хотелось бы предостеречь студентов от необдуманного применения этих типов при решении логарифмических уравнений и неравенств. Использование «слева направо» сужает FDZ, а переход от суммы или разности организмов к логарифму произведения или четверти расширяет FDZ.
Определены два случая. Когда обе функции строго положительны, или когда f(x) и g(x) обе меньше нуля.
Превратите это выражение в сумму
Если f (x) > 0 и g(x) > 0, то мы должны ограничить себя. Это явно неприемлемо, поскольку мы сталкиваемся с сужением области приемлемых цен, что может привести к потере решения. Тип (6) имеет аналогичную проблему.
Сразу после уравнивания первых двух уравнений системы, обратите внимание, что любое из них может быть удалено. Удалите первый. Потому что он выглядит более угрожающе, чем второй.
Логарифмическая функция, её свойства и график
В их математике и приложениях мы часто сталкиваемся с логарифмической функцией y = logax, где a — заданное число, a> 0, \(a \ neq 1 \)
Логарифмическая функция обладает свойствами: 1) Область действия логарифмической функции — множество всех положительных чисел.
(2) Сумма логарифмической функции — это сумма всех действительных чисел.
3) Логарифмическая функция не ограничена.
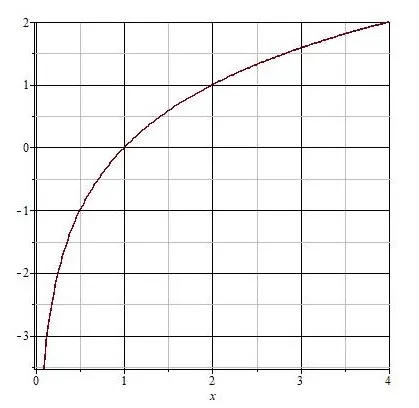
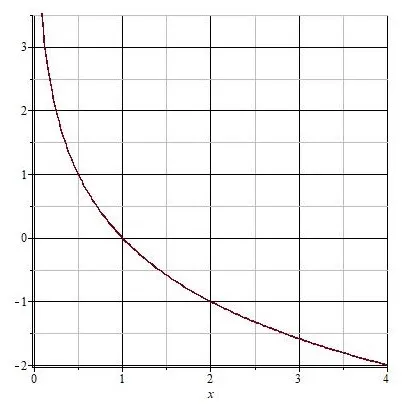
4) Логарифмическая функция y = logax увеличивается, если пространство \(0; +\ infty)\)a> 1 и уменьшается, если 0 1, функция y = logax имеет положительное значение, если x> 1, и отрицательное значение, если 0.
Ось oy часто не является вертикальной осью графика функции y = logaЛетучие мыши.
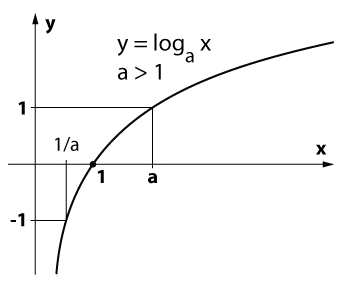
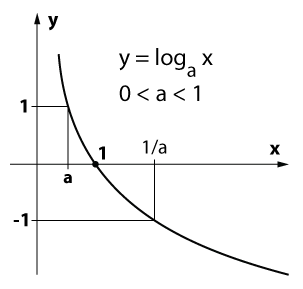
Обратите внимание, что график логарифмической функции y = logax проходит через точку (1; 0). Для решения уравнения часто используется следующая теорема
Логарифмическая функция y = logax и экспоненциальная функция y = a x, где a> 0 и \(a \ neq 1 \) взаимно обратны.
Логарифмические уравнения
Решается логарифмическое уравнение2(x + 1) + log2(x + 3) = 3 Предположим, что x — такое число, что равенство применимо. Другими словами, x является корнем уравнения. Тогда, согласно свойству логарифма, равенство log2((x+1) (x+3)) = 3 Согласно определению логарифмов, это равенство возникает (x+1) (x+3) = 8 x 2+4x+3 = 8, т.е. x 2+ 4x -5 = 0, где x1 = 1, х2 = -5 квадратное уравнение является результатом исходного уравнения и должно быть проверено. Проверьте, являются ли числа 1 и -5 корнями исходного уравнения. Замените x = 1 в левой части исходного уравнения2(1 + 1) + log2(1 + 3) = log22 + log24 = 1 + 2 = 3, т.е. x = 1 является корнем уравнения. Для x = -5 числа x + 1 и x + 3 являются отрицательными и поэтому не имеют значения в левой части уравнения. Другими словами, x = -5 не является корнем уравнения. Ответ: x = 1
Решите уравнение LG (2x 2-4x + 12) = LG x + LG (x + 3) в соответствии с логарифмами LG (2x 2-4x + 12) = LG (x 2 + 3x). x 2 + 3x x 2-7x + 12 = 0 x1 = 3, х2 = 4 проверяет, что оба значения x являются корнями исходного уравнения. Ответ: x1 = 3, х2 = 4
Решается логарифмическое уравнение4(2x — 1) — log4x = 2 log.4(2x -1) Преобразуем это уравнение: log4(2x — 1) — log4x — 2 log4(2x -1) = 0 log4(2x -1) — (log4 (x -2) = 0 Приравняйте каждый множитель из левой части уравнения к нулю 1) log4 (2x -1) = 0, поэтому 2x -1 = 1, x1 = 1 2) log4 x -2 = 0, где log4 = 2, х.2 = 16 проверяет, что оба значения x являются корнями исходного уравнения. Ответ: x1 = 1, х2 = 16
Например, 100 x 1000 можно вычислить путем поиска логарифма 100 на основе 10 и 1000 и нахождения его антагонизма (т.е. числа под знаком логарифма 100000 в данном случае).
Нашли ошибку?
Если вы считаете, что нашли ошибку в учебном материале, напишите на адрес электронной почты (адрес электронной почты здесь). В электронном письме сообщите тему (физическая или математическая), название или номер предмета или теста, номер вопроса или часть текста (страницу). Выявляются ошибки. Также объясните, в чем заключается ошибка. Ваше письмо не останется без внимания, и ошибка будет исправлена или объяснена вам.
Данный сайт или любая его часть не могут быть использованы в коммерческих целях, а также скопированы, перепечатаны, переизданы или воспроизведены в любой форме. Нарушение авторских прав владельца будет преследоваться по закону. Дальнейшее чтение.








