Если символ сравнения строгий («больше чем» или «меньше чем»), сигнал обычно представляет собой бесцветный круг с бесцветной внутренней частью. Если оно не является точным («больше чем» или «меньше чем»), оно закрашивается.
Квадратные неравенства можно решить с помощью графика или чертежа пространства. Смотрите примеры решений неравенства.
Примеры. 1. решите неравенство: $ x ^ 2-2x-80$. Найдите корни триномиального уравнения: $ x_1 =2$ и $x_2=3$.

Постройте график квадратного уравнения так, чтобы ось дивергенции пересекала точки 2 и 3. Если график функции лежит на оси бездны, то квадратный треугольник принимает значения больше нуля. График функции дает ответ: $ 5x-6 Ответ: $ x3$.
3. решите неравенство: 3500 ^ 2 +2x+1≥0$.
Решение: вычислите дискретность и найдите корни тринома: $ D = 2 ^ 2-4 * 2 = -41$ и $x-2$ и $x-2$ и $x0$.
СМИ «mathematics-tests.com» зарегистрировано Федеральным управлением связи и информационных технологий средств массовой информации (Роскомнадзор). Свидетельство о регистрации СМИ EN номер FS77 — 63677 от 10 ноября 2015 года. название — https://mathematics-tests.com.
Основатель сайта mathematics-tests.com: Андреев Г.И., Главный редактор: Андреев Г.И., Телефон редакции: +7 (906) 384-18-43, Email: email protected mathematics-tests.com
Квадратичная функция — это функция вида: ǫ (ǫ displaystyle f \ слева (x \ справа) = a ^> + bx + c = 0 \), ǫ (ǫ displaystyle a \ ne 0 \)
Квадратные неравенства
Что такое квадратичная функция для решения квадратичных неравенств? Квадратичная функция — это функция уравнения y = ax2 + bx + c. где x — независимая переменная, a, b и c — некоторые числа, a. 0. Графиком квадратичной функции является парабола.
В зависимости от величины кривой она раздваивается вверх или вниз.
Как решать квадратные неравенства?
Решите квадратное неравенство, используя примеры. Сначала рассмотрим случай, когда разрешение квадратного уравнения меньше нуля (нет корней).
Поскольку дискриминант равен -236, уравнение не имеет корней. Это означает, что a = 3> 0 (ветви параболы направлены вверх), поэтому весь график параболы лежит на оси x.
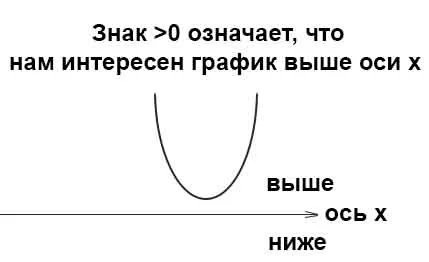
Мы можем проверить себя, взяв любое число с числовой прямой, например, 1. 1 заменяется переменной x в неравенстве 3×2 + 2x +20>0.
Поскольку существует верное неравенство 25>0, все точки на числовой прямой совпадают, так как уравнение не имеет корней.
Рассмотрим тот же пример, где знак неравенства меньше нуля
Поскольку дискриминант меньше нуля — 236, уравнение не имеет корней, и парабола не пересекает ось x. Поскольку a = 3> 0, весь график параболы лежит выше оси x.
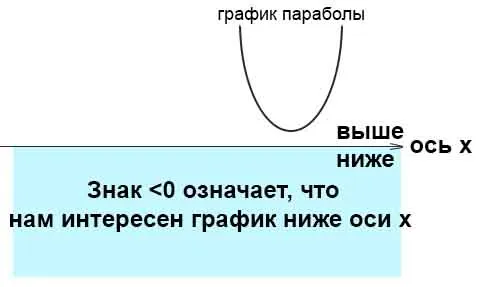
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20
Рассмотрим следующий пример.
Поскольку дискриминант больше нуля, уравнение имеет два корня, и парабола пересекает ось x в точках x = 1 и x = -2. Поскольку a = 1> 0, ветвь притчи смотрит вверх.
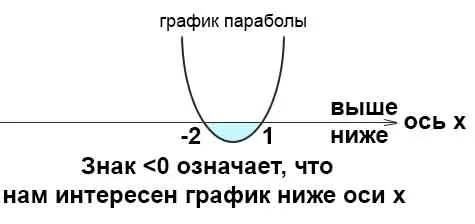
Также можно решить методом интервалов. Ось x делится на три участка. Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x 2 +x-2
Вторая часть — (-2; 1). В этом разделе вы получаете число 0.
Третья часть (1; +∞). В этом разделе вы получите число 2.
Рассмотрим тот же пример с другим знаком неравенства.
Поскольку дискриминант больше нуля, уравнение имеет два корня, и парабола пересекает ось x в точках x = 1 и x = -2. Поскольку a = 1> 0, ветвь притчи смотрит вверх.
Знак уравнения больше, чем > 0. В ответе необходимо записать параболу над осью x. Его можно визуально оценить по изображению. Сопоставьте интервалы (-∞; -2) и (1; +∞).
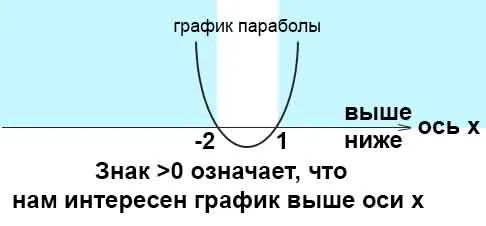
Для решения задачи можно также использовать метод интервалов. Ось x разделена на три части.
Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x 2 +x-2
Неравенство 4> 0 верно, поэтому уместен пробел (-∞; 2).
Вторая часть — (-2; 1). В этом разделе вы получаете число 0.
Так как неравенство -2> 0 неверно, то данный отрезок (-2; 1) не подходит.
Третья секция (1; +∞). В этой области вы получаете второй номер.
Чтобы получить верное неравенство 4> 0, допустим пробел (1; +∞).
You may also like:

Определение числовой функции. Область определения функции. Область значения функции.

Квадратное трио Ax 2 + BX + C — это числовой промежуток под осью скота, даже если вы хотите найти числовой промежуток меньше нуля.
Решение квадратных неравенств
С двумя корнями
Квадратные уравнения решаются методом SO -Caled Space Method. Его принципы заключаются в следующем.
1. все элементы неравенства должны быть сосредоточены в левой части, оставляя в правой части только нули. Помните, что если вы перемещаете один элемент с одного места на другое, его памятование меняется на противоположное.
2.Если неизвестная переменная предшествует отрицательному коэффициенту второй степени, умножьте все элементы неравенства на -1 и поменяйте знак сравнения.
3.Замените знак сравнения на «равно» и решите полученное квадратное уравнение.
4.Отметьте корни на осях чисел.

Если символ сравнения строгий («больше чем» или «меньше чем»), сигнал обычно представляет собой бесцветный круг с бесцветной внутренней частью. Если оно не является точным («больше чем» или «меньше чем»), оно закрашивается.
5. нарисуйте пробел, передавая символы «плюс» и «минус» справа налево (начинайте с «+», затем чередуйте).

6. если символ ‘>’ или ‘≥’ неравнозначен, «» «≤» — отрицательный интервал, требуется положительный интервал.
Пример 1: Решите неравенство квадратов.
Решение: 1. Правая часть должна быть равна нулю, поэтому перенесите число -3 в левую часть и поменяйте его знак на «плюс».
2. найдите корни квадратного уравнения.
Мы подробно рассмотрели эту проблему в другой публикации и не будем рассматривать ее отдельно здесь.
Таким образом, корни этого конкретного уравнения следующие. Обратите внимание на числовые оси (круги не закрашены, так как неравенства строгие).

Отметьте «плюс» и «минус» и нарисуйте точку.

Необходимы только положительные области, так как признаков неравенства «больше».

Отсюда следует решение неравенства.
Примечание: Если рассматриваются другие признаки неравенства, то область решения: «положительное», «отрицательное», «положительное», «отрицательное», «отрицательное», «положительное», «положительное», «положительное».
С одним корнем
Положительное уравнение не всегда имеет два корня, но иногда один.
Пример 2 Решение.
Решение: соответствующее квадратное уравнение имеет только один корень.
Отметьте точку в виде неполной окружности на числовой оси и проведите от нее два интервала.

Поскольку дискриминант больше нуля, уравнение имеет два корня, и парабола пересекает ось x в точках x = 1 и x = -2. Поскольку a = 1> 0, ветвь притчи смотрит вверх.
Другие примеры решения квадратных неравенств
Рассмотрите решение других примеров квадратных неравенств. Необходимо устранить неравенство площадей.
Правая часть неравенства уже содержит нули. В «x 2» мы можем сразу перейти к нахождению корня, потому что это «2» (положительный коэффициент).
Бату.1; 2 =
| −(−1) ± √ (−1 2 ) − 4 · 2 · 0 |
| 2 · 2 |
Рассмотрим пример, в котором квадратное неравенство ‘x 2’ имеет отрицательный коэффициент перед ‘x 2’.
Согласно пункту 2 общего правила решения по закону Вселенной, нам необходимо получить положительный коэффициент перед «x 2». Для этого умножьте все неравенство на «-1».
Важно!
Помните, что умножение неравенства на отрицательное число меняет знаки неравенства.
Вы можете перейти к шагам 4 и 5. Приравняйте левую часть неравенства к нулю и решите полученное квадратное уравнение. Затем расположите полученные корни на числовой прямой и проведите между ними «дугу».
Бату.1; 2 =
| −3 ± √ 3 2 − 4 · 1 · (−4) |
| 2 · 1 |
x1; 2 =
| −3 ± √ 9 + 16 |
| 2 |
Важно!
При определении интервала для ответа нужно начинать с последней версии неравенства, прежде чем находить его корни.
В нашем случае последняя версия неравенства перед нахождением корней уравнения — ‘x 2+3x-4≤0’.
Поэтому в ответе нам нужно выбрать пробел со знаком ‘-‘.
К сожалению, решение квадратичных неравенств не всегда дает два корня и следует общей схеме, описанной выше. Бывают случаи, когда имеется только один корень или корень не получен.
О том, как решать квадратные неравенства в таких случаях, рассказывается в следующем уроке «Квадратные неравенства с одним корнем и без него».
Знак неравенства может представлять собой любое число, а коэффициенты a, b и c могут быть любыми ($a≠0$). Все правила, которые вы установили для линейных неравенств, работают и здесь. Повторите эти правила для себя!
Алгоритм решения квадратных неравенств
1) Напишите квадратное уравнение, соответствующее неравенству (просто поменяйте знак неравенства\(>、\ текст< >\ ge, 모ᢙ текст< >\ le \) знак уравнения «\ (⌘ displaystyle = \)»).
2) Найдите корень этого уравнения:.
(3) Отметьте корни оси ǫ (Ox \) и наметьте направление параболических ветвей («вверх» или «вниз»).
4) Отметьте ось знаком, соответствующим знаку квадратичной функции. Парабола над осью обозначена «ɛ (+ \)», а парабола под ней — «ɛ (- ɛ)».
(5) В зависимости от знака неравенства, опишите один или несколько интервалов, соответствующих «\(+ \)» или «\(-\)». Если неравенство нестрогое, то корень включается в пространство. Если строгий, то корень не включается.
1. все элементы неравенства должны быть сосредоточены в левой части, оставляя в правой части только нули. Помните, что если вы перемещаете один элемент с одного места на другое, его памятование меняется на противоположное.
Определение квадратного неравенства
Неравенства — это алгебраические выражения со знаком ≠, ≤, ≥.
Числовые неравенства — это неравенства, которые содержат числа или математические выражения по обе стороны от точки.
Решением является значение переменной, для которой неравенство верно.
Решить неравенство — значит найти множество, к которому оно относится.
Квадратное неравенство имеет следующий вид.
Квадратные неравенства могут быть решены двумя способами
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c=0. Чтобы найти корни, необходимо найти дискриминант этого уравнения.
Как дискриминант уравнения влияет на корни уравнения?
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень ;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня ;
- D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней .
В зависимости от полученных корней и знака коэффициента α возможно одно из шести возможных положений графика функции y = ax 2 + bx+c.
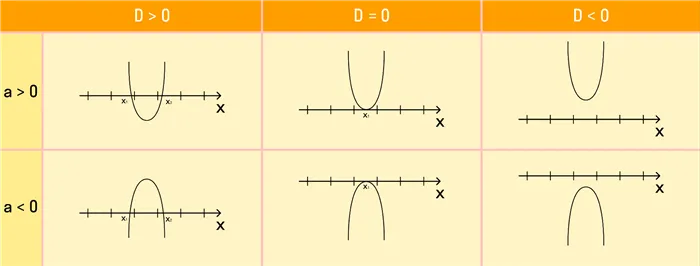
Если вы хотите найти арифметический интервал, в котором площадь треугольника ax2+ bx + c больше нуля, то этот арифметический интервал находится там, где парабола лежит выше оси OX.
Квадратное трио Ax 2 + BX + C — это числовой промежуток под осью скота, даже если вы хотите найти числовой промежуток меньше нуля.
Если квадратное неравенство не является строгим, то корни находятся в арифметическом интервале. В строгих случаях это не так.
Изучение математики в онлайн-школе Skysmart облегчает понимание сложных тем и позволяет получить более высокие баллы на экзаменах.
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >,
Затем вы узнаете об интервалах в контексте решения квадратичных неравенств.
Пробел — это промежуток между цифрами. То есть, все возможные числа, заключенные между двумя числами (край пробела). Поскольку эти пространства нелегко представить, пространства обычно проектируются
Алгоритм решения квадратных неравенств с помощью пространств:.
Если неравенства строгие, то корни следует обозначить пустыми (перфорированными) точками. Если они не являются строгими, используются обычные точки. Эти точки делят оси координат на интервалы.
В результате возникает геометрический образ множества чисел — это и есть решение неравенства.
В качестве альтернативы, вместо разметки, «луки» могут быть оформлены интервалами. Справа налево начинайте с + и чередуйте символы + и -.
Проанализируйте третий шаг алгоритма. Существует несколько подходов к определению точек в интервалах.
Например, используя три имени x 2 + 4x -5, корни которых равны -5 и 1, разделите числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, (1)+∞).
Определите знак трицикла x 2 + 4x -5 в пространстве (1, +∞). Для этого вычислите значения этих трех ИМЕН при некотором значении x, начиная с этого момента. Вы можете получить любое значение переменной, если вычисление простое. В нашем случае мы получаем x = 2. Вместо x мы заменим его на 3 имени.
7 — положительное число. Это означает, что значение квадрата 3 во вселенной (1, +∞) положительно. Поэтому мы определили символ Plus.
Давайте определим два других интервальных знака. Начните с пробела (-5, 1). Отсюда получаем x = 0 и при таком значении переменной можем вычислить значение квадратного тринома.
Поскольку -5 — отрицательное число, все три цены будут отрицательными в течение этого периода. Таким образом, отрицательный знак был идентифицирован.
Осталось определить знак пробела (-∞, -5). Получаем x = -6 и заменяем:.
Таким образом, искомым символом является syn.
Если мы запомним эти события, то сможем быстрее разместить тарелку.
Точка пересечения притчи с осью ǫ (x \) называется нулем функции и является корнем соответствующего квадратного уравнения.
Решение квадратных неравенств с помощью квадратичной функции

В этом видеосюжете мы вспомним, какие неравенства называются квадратными неравенствами, и более подробно рассмотрим, как решать квадратные неравенства, например, графические неравенства. Это напоминает им алгоритм, как он решает подобные неравенства.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к обучающим видео по нему и другим наборам, нужно попасть в список, купить его и добавить в свой личный гардероб.



Конспект урока «Решение квадратных неравенств с помощью квадратичной функции»
— Повторите неравенства, называемые квадратными неравенствами, чтобы
— Чтобы подробно изучить графическое решение квадратных неравенств, перейдите по ссылке
— Напомните алгоритм решения таких неравенств.
Вспомните, что квадратные неравенства — это неравенства формы.

Для решения неравенств такого типа обычно используются два основных метода. Это графический метод и аналитический метод или метод пространства. В любом случае, чтобы решить квадратное неравенство, необходимо сначала решить соответствующее квадратное уравнение.
Сегодня мы повторим графический метод решения квадратных неравенств.
Чтобы применить этот метод, вспомните, что график квадратичной функции — это притча.
Если вы рассмотрите квадратное уравнение вместо неравенства, то узнаете, что уравнение может не иметь корней и иметь один или два корня, в зависимости от знаков характеристических сил.
Решением графического уравнения является расстояние между пересечением сюжета PAR и оси OH.
Это означает, что можно создать таблицу, в которой будут графически представлены все случаи, когда притча пересекает ось OH.
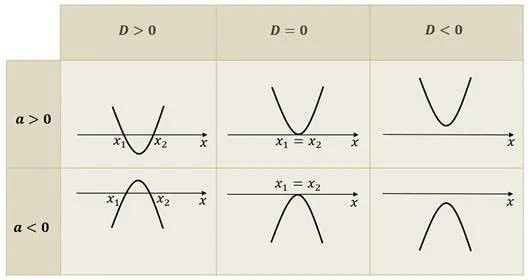
Нетрудно решить квадратные неравенства, найдя корни соответствующих квадратных уравнений.

Давайте рассмотрим несколько примеров.
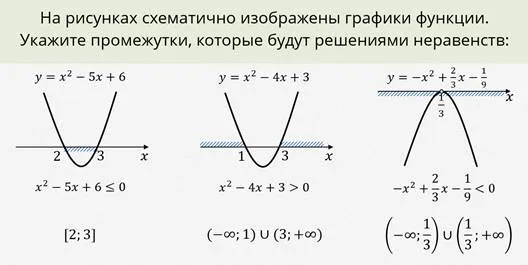
Запомните алгоритм решения квадратичных неравенств, чтобы не пришлось запоминать заполненную выше таблицу.
1. определить направление ветвей притчи.
2.Найдите корни соответствующего квадратного уравнения или установите, что уравнение не имеет корней.
3.Схематически изобразите график квадратичной функции, отметив расстояние между точкой пересечения графика и осью Ох.
4.Используйте график для определения интервала, который является решением неравенства.
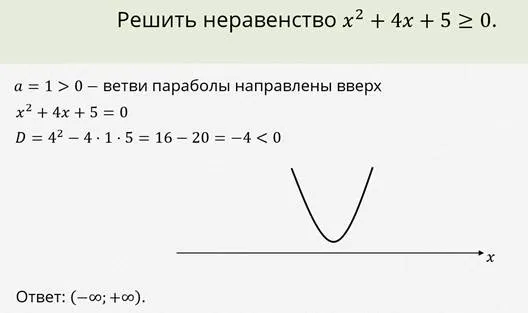
Рассмотрим другой пример.
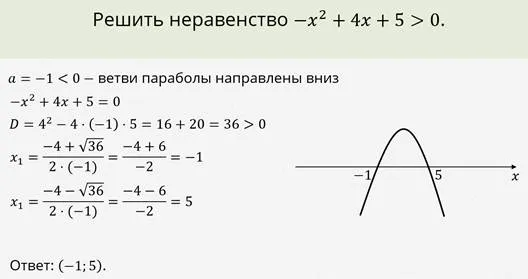
Рассмотрим другой пример.
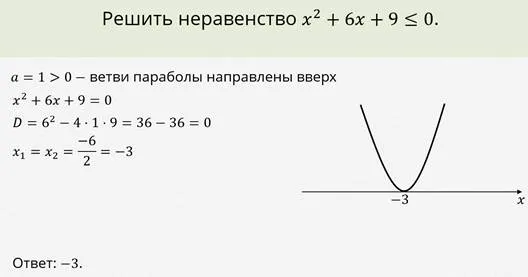
Сегодня на этом уроке вы вспомнили, какие неравенства называются квадратными, и подробно рассмотрели, как решать квадратные неравенства графически. Вы вспомнили алгоритм решения таких неравенств.








