Рассмотрим пример с квадратом корня из корней: Преобразуйте внутренний квадратный корень, применяя формулы, приведенные выше: Теперь преобразуйте исходный квадратный корень: Теперь.
Первый практически важный результат:

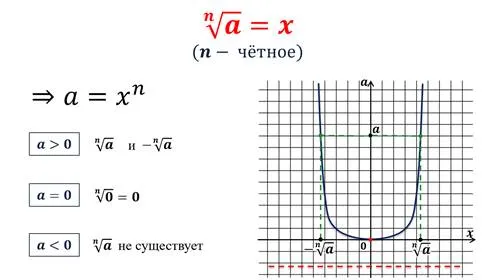
Этот результат в основном отражает определение корня четной степени. Символ ⇔ означает эквивалентность. То есть, приведенную выше нотацию следует понимать так: если, то, и если, то.
С первого равенства системы.
Поэтому в школе мы рассматриваем корни четных степеней состоят только из неотрицательных чисел, мы понимаем их как
Второй практически важный результат:
По сути, они объединяют определение арифметического корня нечетной степени и определение корня нечетной степени отрицательное число. Давайте объясним это.
Из определений, В свете предыдущих разделов становится ясно, что можно понять смысл выражения корням нечетных степеней любого действительного числа, не только неотрицательного, но и отрицательного. Для неотрицательных чисел b принимается равным. Понятно, что для таких определении и Отсюда следует, что корень из нечетного степени 2-k+1 отрицательное число -a является отрицательным числом b, степень 2k+1 из которых равны -a, в алфавитном порядке .
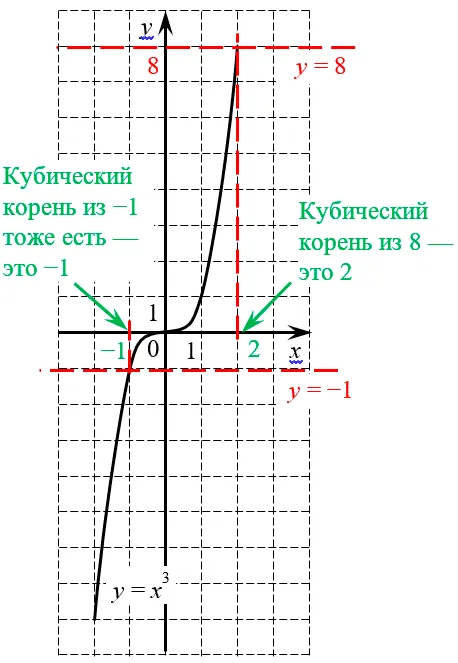
Поэтому в школе мы рассматриваем корни нечетных степеней любых действительных чисел и понимать их следующим образом:
Первое уравнение не имеет решений, а единственным решением второго уравнения является x = 3 6 = 729. Если подставить это число в исходное уравнение, то видно, что оно не является посторонним корнем.
Свойства корней — коротко о главном
Квадратным корнем (арифметический квадрат корнем) неотрицательного числа \( a\) — это неотрицательное число, квадрат которого равен \( a\).
Свойства корней:
Для каждого натурального \( n\), каждого целого \( k\) и каждого неотрицательного числа \( a\) и \( b\) уравнения удовлетворяются:
Арифметический квадратный корень
Как только вы поймете этот предмет, вам будет гораздо легче решать иррациональные уравнения и неравенства.
А пока давайте попробуем разобраться, что это за понятие «корень» и что это такое 🙂 .
Для этого давайте рассмотрим несколько примеров, которые вы уже изучали (или изучите) в классе.
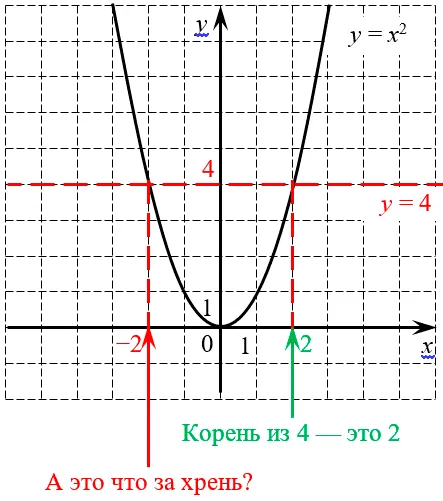
К примеру, перед нами уравнение \( ^>= Каково решение этого уравнения? Какие числа можно возвести в квадрат, чтобы получить \( 4\)?
Если вы помните таблицу умножения, вы легко сможете дать ответ: \( 2\) и \( -2\) (потому что умножение двух отрицательных чисел дает положительное число)!
Для простоты математики ввели специальное понятие для квадрата корня и дал ему специальный символ \( \sqrt\).
Дадим определение В арифметическом квадрате. корню.
Квадратным корнем (арифметический квадрат корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\) \( \left( \sqrt=x,\ ^>=a?)
Почему же число \( a\) должно быть неотрицательным?
Например, что такое \( \sqrt\)? Хорошо, давайте попробуем так. Как насчет трех?
Проверим: \( ^>=9\), а не \( -9\). Как насчет \( \links( -3<<\left( -3 \right)>^>ight)\)? И снова, давайте посмотрим на это: \(
= Так разве это не сочетается? Этого следовало ожидать — ведь нет таких чисел, квадрат которых дает отрицательное число! корня Вы должны помнить, что: число или выражение под символом
должны быть неотрицательными! в определении Однако внимательный наблюдатель, возможно, уже заметил, что корня говорят, что решение квадрата
Кто-то из вас скажет, что в самом начале мы разбирали пример \( ^>»Число \( a\) — это неотрицательное число, квадрат которого равен \( a\)».
=4\), мы выбрали числа, которые можно возвести в квадрат и получили \( 4\), ответ был \( 2\) и \( -2\), и тут кто-то говорит «неотрицательное число»! корня из числа.
Квадратное уравнение или квадратный корень?
К примеру, \( ^>Такое заявление вполне уместно. Здесь нам нужно только провести различие между понятиями квадратных уравнений и арифметических квадратичных уравнений
Из \( ^>=4\) следует, что \( \left| x \right|=\sqrt\), то есть \( x=\pm \sqrt=\pm 2\) или \( _>=2;\ _>=4\) не эквивалентно выражению \( x=\sqrt\).
=-2\).
А из \( x=\sqrt\) следует, что \( x=2\).
Это, конечно, очень запутанно, но необходимо помнить, что символы являются результатом решения уравнения, потому что при решении уравнения мы должны записать все \es, которые при подстановке в исходное уравнение дают правильный результат.
И \( 2\), и \( -2\) подходят под наше квадратичное уравнение.
А теперь попробуй решить такое уравнение \( ^>Однако если мы просто возьмем квадратный корень из чего-либо, мы всегда получим неотрицательный результат.
=3\).
Начнем с самого начала – с нуля: \( ^>Все уже не так просто и гладко, не так ли? Попробуйте поискать цифры, возможно, вы что-то найдете.
Двигаемся дальше \( \text=1;\ ^>=0\) не работает.
А что если \( x=2\); \( ^>=1\) — меньше трех, также отклоняется.
=4\) — тоже не работает, потому что их больше трех.
То же самое происходит и с отрицательными числами., степеннаДля положительных рациональных значений экспоненты n корней степени Функция I является произведением она определена m из x : Для нечетных m, , степенная функция определена для всех вещественных x. Для четного m
Корень n-ой степени
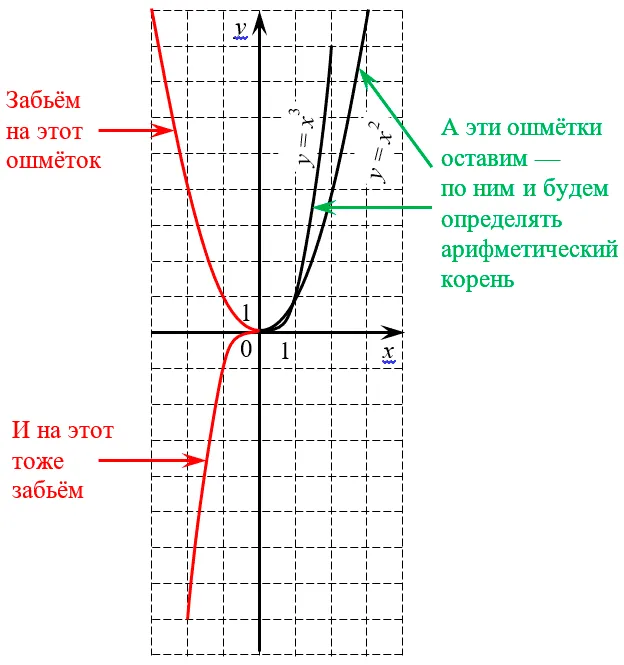
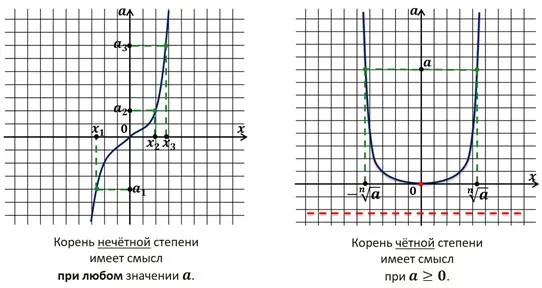
для неотрицательных. степени В этом уроке мы вспомним, как извлечь квадратный корень из n степени числа. Повторяем, что корень из n-го корнем n-ой степени. Так, корень чётной степени неотрицательного числа называется арифметическим корнем. корнем неотрицательного числа всегда А корня чётной степени арифметика и поэтому равна неотрицательному числу. степени отрицательного числа не существует. Квадратный корень из нечетного числа степени неотрицательного числа равно неотрицательному числу. Итак, корень из нечетного корня n-ой степени, неотрицательного числа равно отрицательному числу. Она должна быть выражена арифметическим действием корня. и вычесть знак минус под ним. корня n-ой степени Мы также вспомним свойства арифметики

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
и показать, как их можно применить на конкретных примерах.
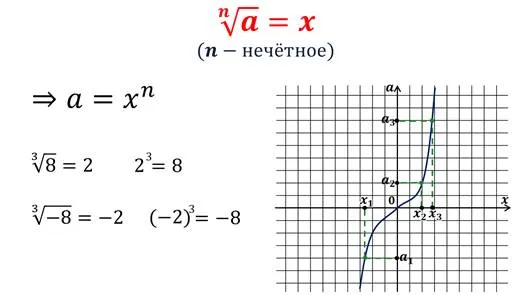
То же самое происходит и с отрицательными числами., степеннаДля положительных рациональных значений экспоненты n корней степени Функция I является произведением она определена m из x : Для нечетных m, , степенная функция определена для всех вещественных x. Для четного m
для неотрицательных .
Пример. Вычислить: $\sqrt5>Пример. Вычислите: $\sqrt4$. Решение. Воспользуемся теоремой 1: $\sqrt4=\sqrt4*\sqrt4*\sqrt4=2*3*4=24$.<\frac>$. Решение. Представим неопределенное выражение в виде неправильной дроби: $7\frac=\frac=\frac=\frac$. Используя теорему 2: $\sqrt5<\sqrt5><\sqrt5>=\frac
=\frac=1\frac$.
Теорема 3. Если $a≥0$, k и n — натуральные числа больше 1, то выполняется следующее равенство: $(\sqrtn)^k=\sqrtn$. степень, Чтобы извлечь корень из натурального числа эту степень достаточно построить
выражение с гипотенузой.
Чтобы извлечь корень из корня, Теорема 4. Если $a≥0$ b n,k — натуральные числа больше 1, то выполняется равенство: $\sqrtn=\sqrtn*k$. корней.
Достаточно умножения экспоненты.
Доказательство. Давайте еще раз кратко докажем это с помощью таблицы. Для доказательства используется упрощенная диаграмма в виде таблицы: Пример. $\sqrt3=\sqrt15$. $\sqrt4=\sqrt8$. $\sqrt=\sqrt4$. корня Теорема 5. Если экспоненты корня не изменится: $\sqrtnp>и выражение subquartn умножаются на одно и то же натуральное число, то значение равно
Доказательство. Принцип доказательства нашей теоремы такой же, как и в других примерах. Введем новые переменные: $\sqrtn*p>=x=>a^
=\sqrtn$, что мы и должны были доказать. корня Число под знаком квадрата числа корня называется знаковым числом, а выражение под знаком
Графики степенной функции
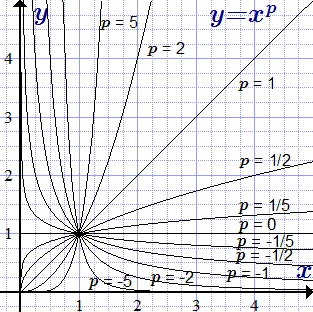
Графики степенно- является подчиненным выражением, и термин «подчиненное число» часто заменяется термином «подчиненное выражение». В символизме, например, выражение a является подчиненным выражением.
Графики функции y = x p для различных значений p. степенной функции, определенной Вот графики функции для неотрицательных значений члена x. Графики
Обратная функция
Обратной для степеннодля отрицательных значений x, см. страницу «Силовая функция, ее свойства и графики». степеннаПервая функция с экспонентой p
i функция с экспонентой 1/p. φ определен не однозначно: ,
Рассмотрим функцию комплексной переменной z : f ( z ) = z t. Выразим комплексную переменную z через коэффициент r и аргумент φ ( r = |z| ) : z = r e i φ. Представим комплексное число t в виде его действительной и мнимой частей: t = p + i q. Тогда мы имеем: Тогда мы считаем, что аргумент. степени Рассмотрим случай, когда q = 0, т.е. экспонента
— является действительным числом, t = p. Тогда. степени, Если p — целое число, то kp — целое число. В силу периодичности тригонометрических функций: То есть, функция экспоненты для целочисленной экспоненты.
для данного z, имеет только одно значение и поэтому не вызывает разногласий.
Если p иррационально, то произведения kp с любым k не дают целого числа. Так как k выполняет бесконечный ряд значений k = 0, ±1, ±2, ±3,. то функция z p имеет бесконечное множество значений. Каждый раз, когда аргумент z получает приращение в 2 p (один оборот), мы переходим к новой ветви функции.0Если p рационально, то его можно представить следующим образом: где m, n — целые числа без общих делителей. Первые n значений, для k = k 0 = 0, 1, 1, 2,. n-1, можно получить n различных значений для kp :. Последующие значения, однако, дают значения, отличающиеся от предыдущих на целое число. Например, если k = k 0 + n, имеем:. Тригонометрические функции, аргументы которых отличаются на кратные 2 π, имеют равные значения. Таким образом, при дальнейшем увеличении k мы получим те же значения для z p, что и при k = k
= 0, 1, 2,. n-1. степени Таким образом, экспоненциальная функция с рациональной экспонентой
В частности, корень степени является полиномиальным и имеет n значений (ветвей). Каждый раз, когда аргумент z увеличивается на 2 p (один оборот), вызывается новая ветвь функции. После n таких вращений мы возвращаемся к первой ветви, с которой начали. й степени n имеет n значений. В качестве примера рассмотрим корень из n -…0положительного действительного числа z = x. В этом случае φ корня, = 0, z = r = |z| = x ,. Таким образом, для квадрата
n = 2, для четных k, ( — 1 ) k = 1. Для нечетных k, ( — 1 ) k = — 1. То есть, квадратный корень имеет два значения: + и — .
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и студентов высших учебных заведений, Лань, 2009. корни $n$-й степени. Именно по этой причине математики степени По этой причине был придуман радикальный символ $\sqrt$. Для обозначения числа $b$, которое в
Замена иррационального уравнения системой
даст нам заданное значение.
Чтобы избавиться от корней, иногда вводят дополнительные переменные, и вместо иррационального уравнения получается множество целых чисел, составляющих систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите уравнение.
Решение. Замените первый корень на u, а второй — на v:
Исходное уравнение имеет вид от корней), то получим:
Если (1) и (2) возвести в куб и квадрат соответственно (для получения

Уравнения (3), (4) и (5) образуют систему с тремя неизвестными и без корней:
Давайте попробуем решить эту проблему. Давайте сначала сложим (4) и (5), так как это позволит нам избавиться от переменной x:
(x + 6) + (11 — x) = u 3 + v 2
Из (3) видно, что v = 5 — u. Подставьте его в (6) вместо v:
17 = u 3 + (5 — u) 2
17 = u 3 + u 2 — 10u + 25
u 3 + u 2 — 10u + 8 = 0 корни. Получаем кубическое уравнение. Мы уже знаем, как решить эту проблему, взяв что корнямНе вдаваясь в подробности решения, мы просто упомянем об этом,
а числами в этом уравнении являются
Подставим эти значения в (4):
x + 6 = 1 3 или x + 6 = 2 3 или x + 6 = (- 4) 3
x + 6 = 1 или x + 6 = 8 или x + 6 = — 64
x = — 5 или x = 2 или x = — 70 корни. Таким образом, мы нашли три возможных значения для x. Но, конечно, среди них могут быть и странные значения.
Поэтому нам нужна проверка — давайте заменим результаты в исходном уравнении. Если x = — 5, то

Корень подходит. Проверьте следующее число, x = 2:

Корень снова правильный. Остается последний тест для x = — 70:
Уравнения с «вложенными» радикалами
Таким образом, все три числа проходят проверку.
Иногда под символом корня уравнения находится еще один корень. Вот пример такой проблемы:
Когда вы решаете проблему, вы сначала устраняете «внешний корень», а затем можете заняться внутренним корнем. Поэтому в данном случае мы сначала возвели в квадрат обе части уравнения:

Внешний корень исчез. Теперь перенесем суммы так, чтобы остался только корень в одной из частей:
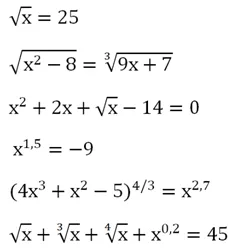
Мы хотим разделить полученное уравнение (1) на x, но важно помнить, что деление на ноль запрещено. То есть, когда мы делим на x, мы должны наложить дополнительное условие: x ≠ 0. В случае, когда x по-прежнему равен нулю, мы рассматриваем отдельно. Для этого подставим x = 0 в исходное уравнение: корнем. Мы получили правильное уравнение, поэтому 0 — это
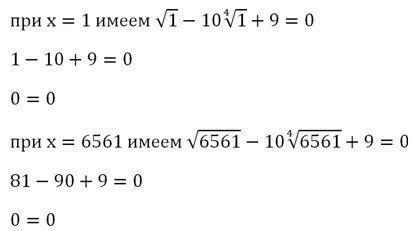
Теперь вернемся к (1) и разделим его на x :
Квадрат, и мы имеем:
x 2 + 40 = (x + 4) 2
x 2 + 40 = x 2 + 8 x + 16. корня:
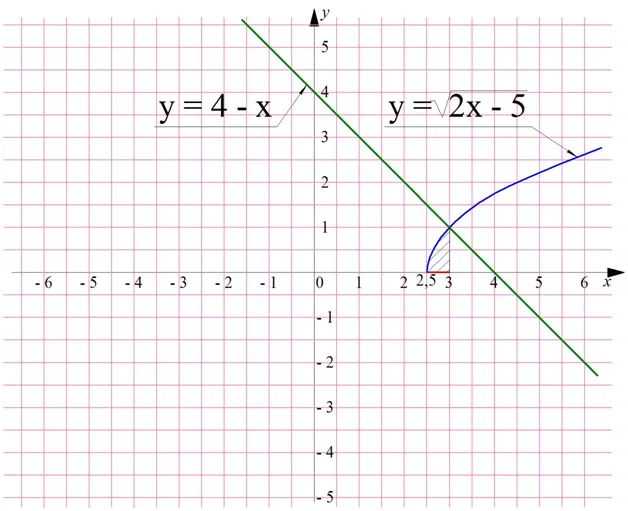
Иррациональные неравенства
Опять же, не лишним будет проверить степень. По аналогии с иррациональными уравнениями, иррациональные неравенства — это такие неравенства, в которых выражение с одной переменной находится под корнем или преобразуется в дробь
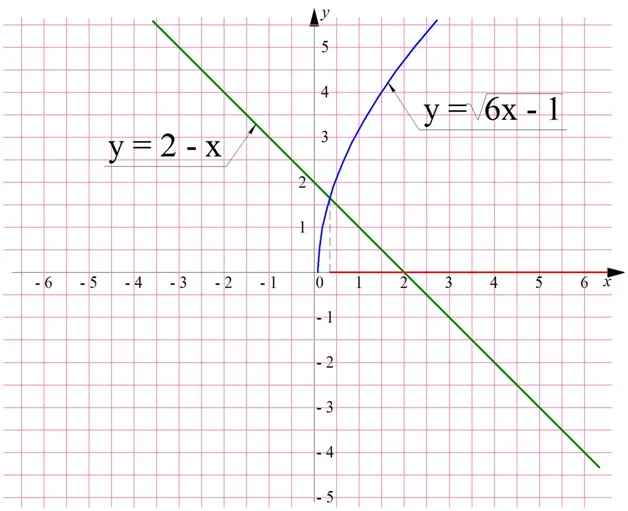
Приведены примеры иррациональных неравенств:
Нет смысла решать проблемы иррациональных нервов, когда есть проблемы с более простыми, то есть рациональными, нервами и их системами. Поэтому, в качестве предосторожности, прочитайте это и это. под корнем, Начните с решения более простых иррациональных неравенств, одна из частей которых содержит выражение
и постоянное число в другой части. Достаточно очевидно, что иррациональное неравенство вида
может иметь место только в том случае, если в степень. То есть, грубо говоря. степень корня Однако это может привести к неактуальным решениям. Следует отметить, что выражение субконъюгата не обязательно должно быть отрицательным, если
равномерно. Поэтому нерв
можно заменить системой нервов, если n четное.
Пример. Для каких значений x это применимо?
Решение. С одной стороны, квадрат нерва дает этот нерв:
Однако подынтегральное выражение должно быть неотрицательным, т.е.
Пример. Решите эту дерзость степень:
Решение. Четырехглавый нерв
x ⩽ — 5 (знак нерва изменился, потому что мы разделили его на отрицательное число).
Возьмем интервал x∈(- ∞; — 5). Кажется, необходимо написать еще один нерв
так, чтобы подконъюгатное выражение было неотрицательным. Однако сравните (1) и (2). Очевидно, что если верно (1), то верно и (2). Если выражение больше или равно двум, то оно автоматически больше нуля! Поэтому (2) не требует решения. с корнем нечетной степени.
Давайте теперь рассмотрим более простой нерв.
Пример. Найдите решение этой щеки.
Решение. Это очень просто — нужно просто взять обе части и поместить их в куб: степени, Возьмите неравенство второго.
Мы уже знаем, как решить эту проблему. Мы помним, что сначала нужно решить уравнение
D = b 2 — 4ac = (- 7) 2 — 4-1-(- 8) = 49 + 32 = 81

Затем отмечаем определенные точки на координатной прямой. Они делят его на несколько интервалов, в каждом из которых функция y =x 2 — 7x- 8 сохраняет свой знак. Тот же знак можно вывести из направления ножек схематически изображенной параболы:
Мы видим, что парабола лежит в интервале (- 1; 8) ниже оси O. Следовательно, этот интервал является ответом. Числа (- 1) и 8 НЕ входят в ответ, т.е. интервал записывается в скобках. степени, Примечание: Поскольку выходной нерв использует единственный (третий) корень.
Нет необходимости в том, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда правая часть нерва является не постоянным числом, а выражением с одной переменной, т.е. имеет вид степень.








