То же самое относится и к треугольной конструкции. Единственное, есть три угла — один для вершины, один для вершины и один для вершины. Это означает, что три точки на плоскости предназначены для представления вершин.
6 класс «Координатная плоскость» план-конспект урока по алгебре (6 класс) на тему
7. учебник по базовой математике. 6 класс: Учебник для общеобразовательных учреждений/Н.Гиа.-Μ.: Μνημοζίνα, 2010. -88σ.: Болезнь.
Тема: «Уровни координат».
- Ввести понятие координатной плоскости;
- Научить учащихся строить точки на координатной плоскости;
- Научить учащихся определять координаты точек, построенных на координатной плоскости
- Демонстрация тесной связи предметов истории, географии, астрономии и математики.
- Расширение кругозора учащихся.
- Развитие приёмов умственной деятельности, памяти, внимания, умения сопоставлять, анализировать, делать выводы.
- Повышение информационной культуры учащихся, интереса к предмету.
- Развитие познавательной активности, положительной мотивации к предмету.
- Развитие потребности к самообразованию.
- Воспитание культуры личности, отношения к математике, как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
- Воспитание ответственности, самостоятельности, умения работать в коллективе.
- Показать математику, как интересную науку, превратить занятие в необычный урок, где может проявить себя каждый ученик.
- Воспитание уважения друг к другу, к старшему поколению.
- закрепить у учащихся понятия: система координат, координатные оси (ось абсцисс, ось ординат), координатная плоскость, абсцисса и ордината точки;
- закрепить у учащихся умения и навыки определять координаты точки, заданной в координатной плоскости, и отмечать точку с заданными координатами в координатной плоскости;
- ставить цели и планировать деятельность по их достижению;
- уметь добывать нужную информацию, используя доступные источники (справочники, учебники, словари, СМИ, глобальной сетью Internet), передавать ее;
- совершенствовать навыки работы в команде, учить высказывать и аргументировано отстаивать своё мнение;
- вносить посильный вклад в достижение общего результата;
- умение брать на себя ответственность при руководстве мини-группой;
- прививать навыки самостоятельной творческой работы;
- учить грамотно использовать в речи математические термины;
- учить применять математические знания и умения в реальных ситуациях;
- прививать навыки самоконтроля и взаимоконтроля;
- совершенствовать графическую культуру.
Оборудование: компьютер, проектор, карточки.
Тип курса: введение в новые знания.
Здравствуйте! Улыбнитесь друг другу и приготовьтесь к хорошей и плодотворной работе. (Учитель оценивает готовность учащихся к уроку.) Садитесь.
Ребята, послушайте, как тихо!
Это начало учебного дня.
Мы не будем терять времени.
Давайте приступим к работе.
Студенты спокойно участвуют в учебной деятельности.
Манипулируйте координатными линиями. (Обратите внимание на экран). Прозрачность 2.
1.Что такое координатная линия?
2.Как называется точка координат (0)?
3.Как располагаются числа на координатных линиях?
4. что обозначают координаты точки?
5.Какие координаты показывают точки на координатной линейке?
6.Какие прямые называются параллельными и перпендикулярными?
По теме: методические разработки, презентации и конспекты

Практическая работа «Построение углов между уровнями и между линиями и уровнями».
Практические работы по геометрии, 10 класс. Эта работа может быть выполнена в качестве подготовки к единым государственным экзаменам по математике, например, С2, решение задач. Проект включает восемь упражнений на построение углов между прямыми и плоскостями.

Взаимное расположение линий и уровней в пространстве. Углы между прямыми и плоскостями.
Эти работы основаны на теме «Взаимное расположение линий и уровней в пространстве». Углы между линиями и уровнями» можно использовать для исследования темы «Углы между линиями и уровнями». Работы представлены в виде таблиц.
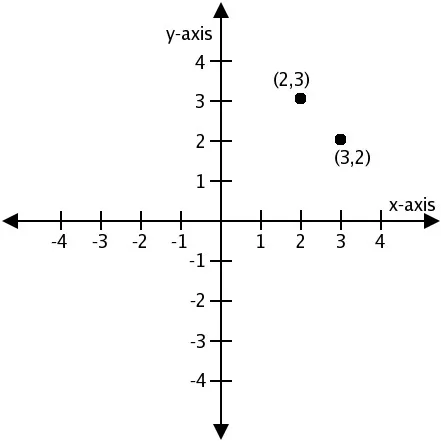
Презентация на тему «Координаты на плоскости», часть 1: «Линии на плоскости».
Первая часть блока учебных презентаций «Координаты на плоскости» Линии, радиусы, отрезки, параллельные прямые, параллельные радиусы, параллельные отрезки, построение параллельных прямых, перпендикуляр.
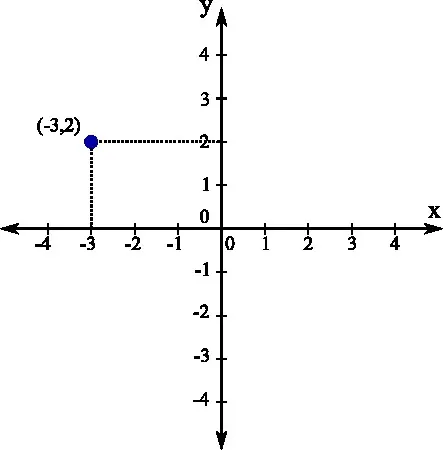
Презентация на тему «Координаты на уровне», часть 2 «Уровни координат».
‘Coordinatesinplane’, часть 2 блока учебных презентаций Координаты, координатные оси, уровневая система координат, координатная плоскость, одноточечная координатная ось, одноточечная координатная ось.
Введение. Предметы геометрии. Аксиомы геометрии. Параллельные линии в пространстве. Параллельные прямые и плоскости. Решение задач: «Параллельные линии и уровни».
Космос слишком мал. Тест по темам «Параллельные прямые, прямые и плоскости» и «Перпендикулярные прямые, прямые и плоскости».
Тесты предназначены для проверки усвоения следующих понятий и определений: взаимное расположение прямых в пространстве, определение пересекающихся прямых, определение параллельных прямых, обозначения параллельных прямых.
Вычислять методы координат и находить углы между прямыми и плоскостями и между плоскостями.
Рассмотрим метод координат, который использует уравнения плоскости для решения задач определения угла. Покажите превосходство этого метода над другими методами и эффективность использования этого метода.
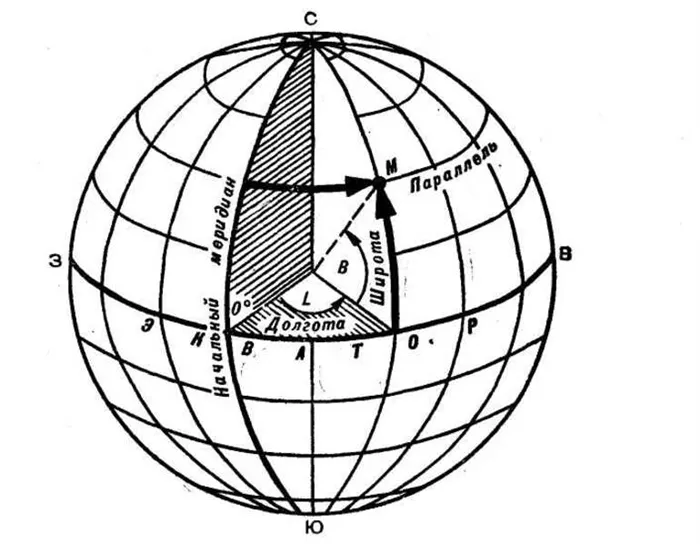
Все точки на одной широте соединены параллельно. На экваторе широта равна 0°, на полюсе — 90°. Меридианы соединяют точки с одинаковой долготой и сходятся на полюсах.
Координатная плоскость
Декартовы или декартовы системы координат являются наиболее распространенными плоскостными и пространственными системами координат.
Декартова система координат на плоскости образована двумя осями с координатами X’X и Y’Y, перпендикулярными друг другу. Координатные оси пересекаются в точке O, называемой принципом координат, и каждая ось имеет положительное направление. Положительное направление осей (правая система координат) выбрано таким образом, что при повороте оси X’X на 90° против часовой стрелки ее положительное направление совпадает с положительным направлением оси Y’Y. Четыре угла (I, II, III и IV), образованные координатными осями X’X и Y’Y, называются координатными углами (см. рис. 1).
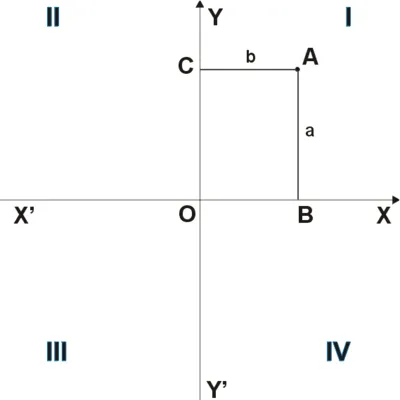
Положение точки A на плоскости определяется двумя координатами x и y. Координата x — длина отрезка OB, а координата y — длина отрезка OC в выбранной единице измерения. Сечения OB и OC определяются линиями, проведенными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется дистальным положением точки A, а координата y — правильным положением точки A. Это описывается следующим образом: a (x, y).
Если A находится под координатным углом I, то A находится под положительным дистальным углом и нижним углом. Если A находится под координатным углом II, то A имеет отрицательный дистальный и положительный правый угол. Если A находится под координатным углом III, то A имеет отрицательное расстояние и отрицательную правую сторону. Если A находится в координатном угле IV, то A имеет положительное расстояние и отрицательную прямую.
Прямоугольная система координат в пространстве
Декартова система координат в пространстве образована тремя координатными осями, перпендикулярными друг другу, OX, OY и OZ. Координатные оси пересекаются в точке O, называемой принципом координат, и каждая ось имеет положительное направление, обозначенное стрелкой, и единицу измерения для отрезка на оси. Единицы измерения одинаковы для всех осей. OX — горизонтальная ось, OY — вертикальное направление оси, OZ — аппликативная ось. Положительное направление осей выбрано таким образом, что при повороте оси OX на 90° против часовой стрелки, когда этот поворот наблюдается с положительного направления оси OZ, ее положительное направление совпадает с положительным направлением оси OY. Эта система координат называется правой системой координат. Когда большой палец правой руки находится в направлении X, указательный палец — в направлении Y, а средний палец — в направлении Z, формируется правосторонняя система координат. Левая система координат образована теми же пальцами левой руки. Левая и правая системы координат не могут быть выровнены так, чтобы их оси совпадали (см. рис. 2).
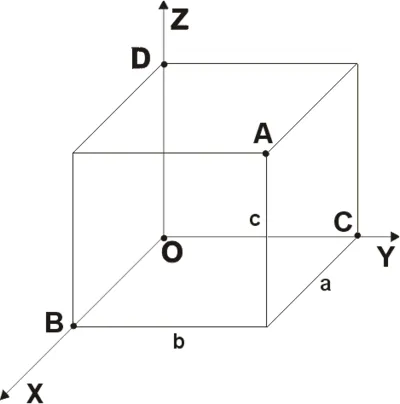
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x — это длина OB, координата y — длина OC, а координата z — длина OD выбранного блока. Сечения OB, OC и OD определяются плоскостями, проведенными из точки A и параллельными плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, а координата z — аппликатой точки A. Он описывается следующим образом: a (a, b, c).
( Декартова система координат (любой размерности) также описывается серией декартовых координат, выровненных по координатным осям. Декартовы числа равны размерам системы координат и все они перпендикулярны друг другу.
В трех измерениях эти прямоугольные точки обычно обозначаются буквой ijk или e.бату ey ez Для правосторонних систем координат применяются следующие типы с вектор-векторными произведениями
История
Прямоугольная система координат была впервые представлена Рене Декартом в его исследовании «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат также называют декартовой системой координат. Метод координат в описании геометрических объектов заложил основы аналитической геометрии. Пьер Ферма также внес свой вклад в развитие метода координат, но его работы были опубликованы только после его смерти. Декарт и Ферма применяли метод координат только к уровням.
Метод трехмерного пространства был впервые реализован Леонгардом Эйлером в 18 веке.
Существует также альтернативный метод — система координат полярного локуса. В этой системе положение точки определяется значением координатной прямой и высотой точки на этой прямой. Это задается углом.
Историческая справка
Идея системы координат возникла еще в эпоху Птолемея. Уже астрономы и математики думали о том, как научиться определять положение точки на уровне. К сожалению, не было известной системы координат, и ученым пришлось использовать другие системы.
Первоначально они определили точки широты и длины. Долгое время это был один из самых распространенных способов обозначения или информации. Однако в 1637 году Рене Декарт создал свою собственную систему координат. Позже она была названа в честь великого математика Декарта.

После публикации «Геометрии» система координат Рене Декарта была признана в научных кругах.
Уже во второй половине XVII века в математическом мире получила широкое распространение концепция «уровней координат». Спустя столетия после создания этой системы она по-прежнему широко используется в математике и в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, я приведу пример, показывающий некоторые уровни координат, чтобы вы могли их представить. Система координат в основном используется в шахматах. Каждый квадрат в таблице имеет свои координаты. Это координатная буква, второй цифровой символ. С его помощью можно определить данную позицию или положение дорожки на шахматной доске.
Второй яркий пример — любимая игра Battleship. Во время игры вспомните координаты, например, B3, и запомните, как точно указывать на цель. В то же время, позиционируя корабль, вы задаете точки на уровне координат.
Эта система координат широко используется не только в математических и рациональных играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
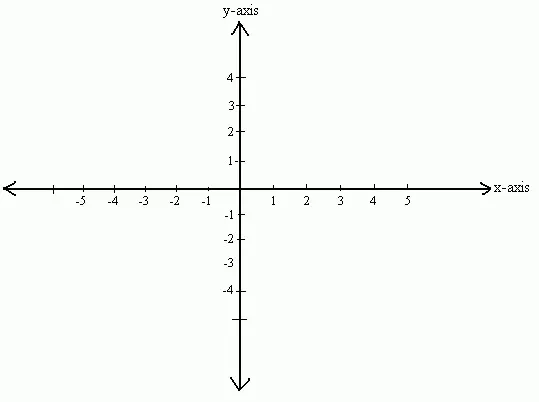
Как уже упоминалось, в системе координат различают две оси. Они очень важны.
Первая ось, бездна, является горизонтальной. (бык). Вторая ось, линия, проходит вертикально от начала и называется (oy). Эти две оси образуют систему координат, которая делит плоскость на четыре четверти. Начало находится на пересечении этих двух осей и принимает значение 0. Уровень регулировки существует только в том случае, если плоскость образована двумя осями, пересекающимися перпендикулярно и имеющими принцип.
Обратите внимание, что каждая ось имеет свое направление. При построении системы координат принято указывать направление оси в виде стрелки. Также каждая ось подписывается при построении уровня координат.
Чтобы определить и записать точное положение любой точки A, необходимо измерить ось края и ее расстояние от заказанной точки. Схема координат может выглядеть так: a (x, y) или x A, xB, возможны и другие варианты.
Виды координатных плоскостей.
Многие люди не знают, что существует два различных уровня координат. Это декартова система координат и полярная система координат.
Первая — это хорошо известная координатная сетка с двумя координатными осями. Этот тип сетки крепится к прицелу телескопа. В этой системе положение точки на плоскости определяется двумя значениями координат.
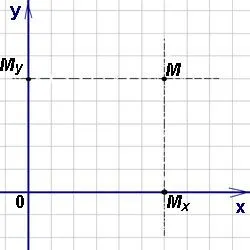
Рисунок 1. Декартова система координат.
Существует также альтернативный метод — система координат полярного локуса. В этой системе положение точки определяется значением координатной прямой и высотой точки на этой прямой. Это задается углом.
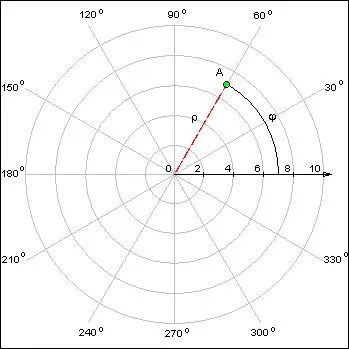
Рисунок 2. Полярная система координат.
Эта система использовалась древними мореплавателями задолго до того, как была изобретена наиболее удобная декартова система. Однако до сих пор полярная система координат имеет свое применение.
Оси координатной плоскости
Оси координатной плоскости — это две вертикальные линии, обозначенные единичным отрезком. Пересечение двух линий служит начальной точкой и центром системы.
Секции блоков осей не должны перекрываться. Таким образом, 1 на оси x — это 1 см, а 10 на оси y — 1 см. Это обычная практика, которая используется для того, чтобы сделать чертежи, планы и графики более понятными на координатном уровне.
Координатные оси традиционно представляются через x и y, называемые абсциссой и ординатой соответственно.
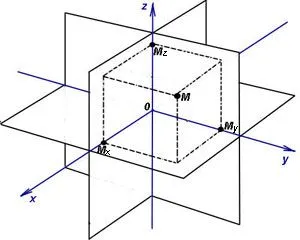
Рисунок 3.Декартова система координат в пространстве.
Аналогичная система координат используется и в пространстве, только добавляется еще одна ось z.
Определение координат
Чтобы определить координаты точки, к каждой оси проводят перпендикулярную линию. Получены два линейных сегмента. Значения длины этих отрезков в указанных единицах длины соответствуют координатам точки.
Поэтому, чтобы построить точку из координат, необходимо провести перпендикулярную линию из определенной точки на оси. Точка пересечения этих перпендикулярных линий является искомой точкой.
В координатной плоскости есть четыре квадранта, каждый из которых имеет свои границы x и y. Обратите внимание, что координаты могут быть отрицательными. Это позволяет определить только одну четверть координатного уровня.
Мы знакомы с системами координат кинотеатров (порядковые номера и номера мест), поездов (номера вагонов и места) и географическими системами координат (долгота и широта).
Особенности использования в географии
Последние достижения в области технологий значительно упростили определение географических координат.
Достаточно запустить одно из навигационных приложений или войти в специальный веб-сервис, и местоположение будет отображено с высочайшей точностью.
Поверхность Земли сферическая, и по этой причине система координат обладает своими уникальными свойствами.
Все части Земли обозначены серией цифр и букв.
- широта бывает северная и южная;
- долгота — восточная и западная;
- высота над уровнем моря.
Все точки на одной широте соединены параллельно. На экваторе широта равна 0°, на полюсе — 90°. Меридианы соединяют точки с одинаковой долготой и сходятся на полюсах.
Определение 4. Края точки A — это координаты точки A.1 На числовой оси Ox прямой угол точки A является координатой точки A.2 На числовой оси Oy.
Уравнение окружности на координатной плоскости
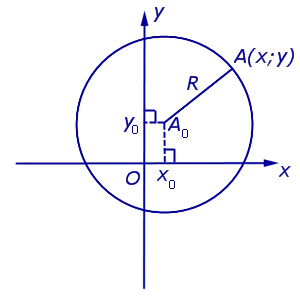
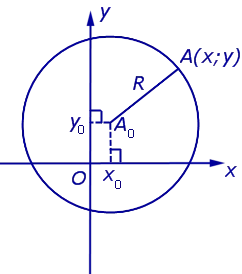
Так как расстояние от любой точки окружности до центра равно радиусу, то согласно уравнению (1) имеем
Уравнение (2) требуется для окружности радиуса R с центральной точкой A.0 (vat.0 ; y0)
Результат. Уравнение для окружности радиуса R с центром в начале координат имеет вид








