Касание к окружности. Какая точка называется точкой касания прямой и окружности

Содержание

Если касательная и вторичная проектируются метками вне круга, то квадрат длины касательной равен квадратику вторичной составляющей: mc 2 = ma-mb.

Какая точка называется точкой касания прямой и окружности

Предмет курса. Тенденция кругов.

Образовательные – повторение, обобщение и проверка знаний по теме: “Касательная к окружности”; выработка основных навыков.
Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Ввести понятие касательной, точки касания.
Рассмотреть свойство касательной и её признак и показать их применение при решении задач в природе и технике.

Задачи урока

Формировать навыки в построении касательных с помощью масштабной линейки, транспортира и чертежного треугольника.
Проверить умение учащихся решать задачи.
Обеспечить овладение основными алгоритмическими приёмами построения касательной к окружности.
Сформировать умения применять теоретические знания к решению задач.
Развивать мышление и речь учащихся.
Работать над формированием умений наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии.
Привитие интереса к математике.

Появление понятия касательной.
История появления касательной.
Геометрические определения.
Основные теоремы.
Построение касательной к окружности.
Закрепление.

Появление понятия касательной

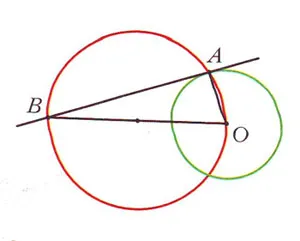
Понятие касательной — одно из самых древних в математике. В геометрии касательной к окружности называется линия, которая имеет ровно одно пересечение с окружностью. Древние использовали компас и линейку, чтобы провести линию по кругу, с ошибками, преувеличениями и притчами, позже — с коническими насечками.

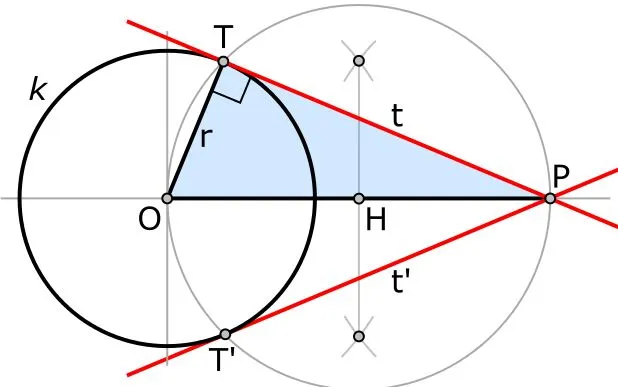
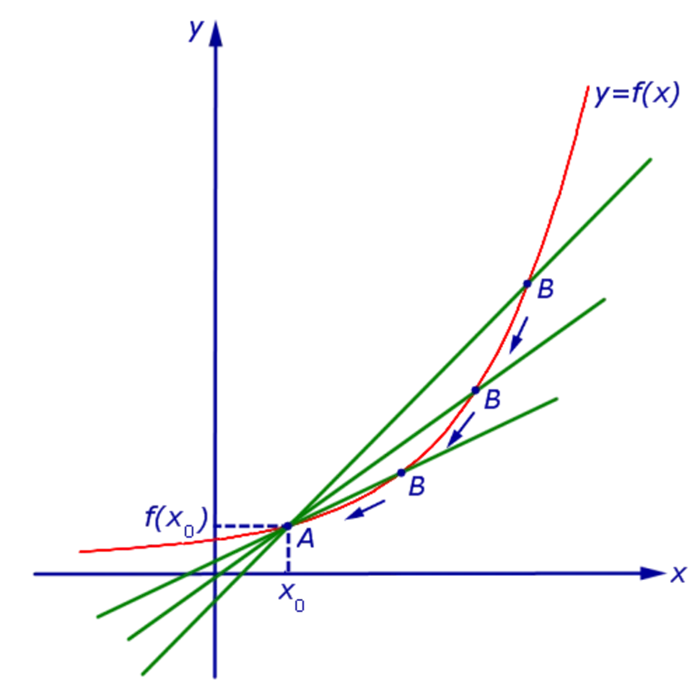
В наше время интерес к плохому возродился. Были обнаружены вещи, которые в то время были неизвестны древним ученым. Например, Галилей ввел циклы, Декарт и Фермат вступили с ними в контакт. В первой трети XVII века стало понятно, что касательная — это линия, «примыкающая» к кривой в небольшой окрестности в определенной точке. Легко представить себе ситуации, когда невозможно построить касательную к кривой в определенной точке (форме).

В первом случае линия параллельна вертикальной оси, во втором случае используется ось абсцисс. Чтобы написать уравнение прямой, необходимо определить, к какой из функций принадлежат точки, заменяющие текущее уравнение. Затем вам нужно их идентифицировать.

Касательная

Касательная линия — это линия, имеющая только одну общую точку с окружностью.

На рисунке AB — касательная линия, касающаяся окружности в точке a.

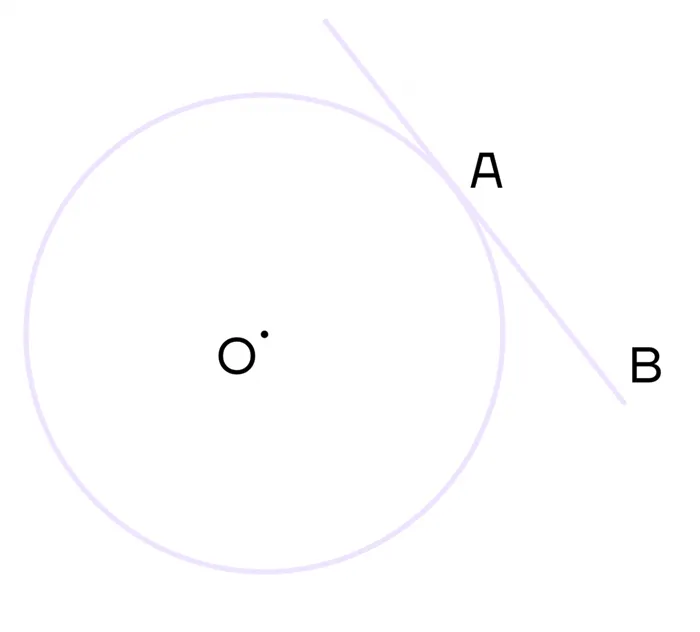
Многие вещи вокруг нас имеют плавные формы. Например, если вы посмотрите на велосипедную цепь, она имеет изогнутую форму.

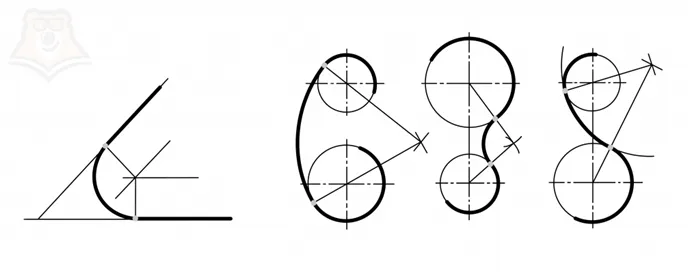
Свойства касательной

1 Собственность. Касательная линия перпендикулярна радиусу, вырезанному из центра окружности в точке касания.

Нарисуйте луч OA, затем OA ab.

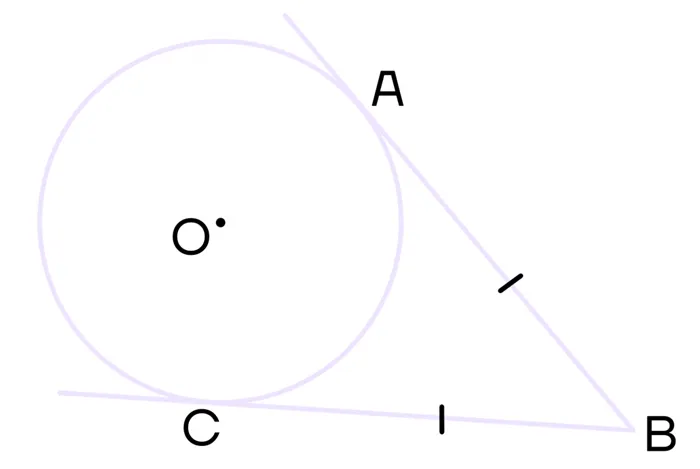
2 Собственность. Если из одной точки проведены две касательные, то их части равны.

Проведите еще одну касательную BC из точки B, тогда ab = bc.

Оглянувшись на форму, вы увидите, что она похожа на воздушный шар. Канаты одинаковой длины используются в возможностях шара и касательной.

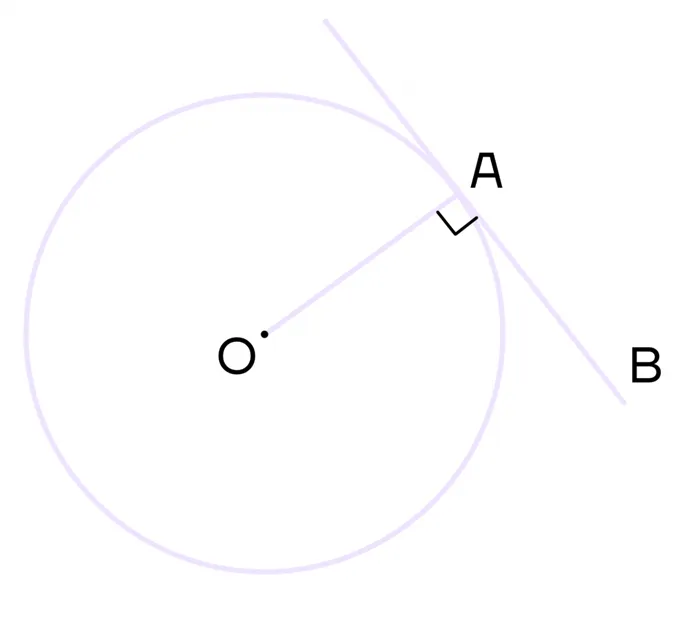
3 Недвижимость. Угол между струной и касательной равен половине дуги, заключенной между касательной и струной.

Нарисуйте струну переменного тока. Тогда угол cab равен ྫྷ(Lo_FRAC⋃acྫྷ).

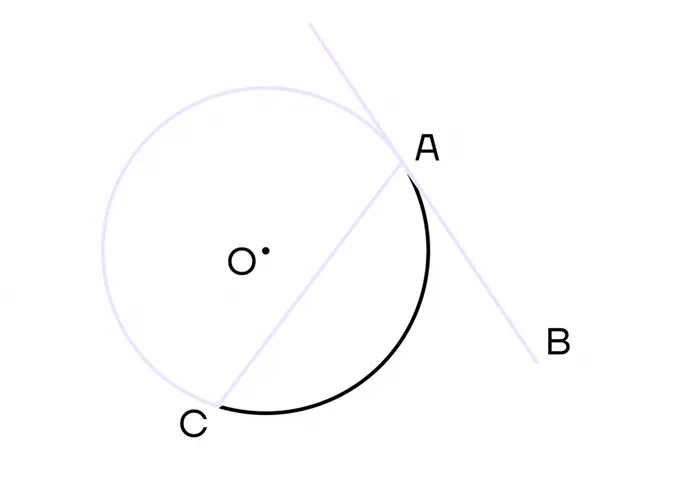
Секущая

Далее рассмотрим третий случай, когда линия пересекает окружность. Такая линия называется вторичной.

Вторичные линии — это линии, пересекающие окружность в двух точках.

Если предположить, что AB — это вторичка на диаграмме, то точки A и B — это пересечения и вторички цикла.

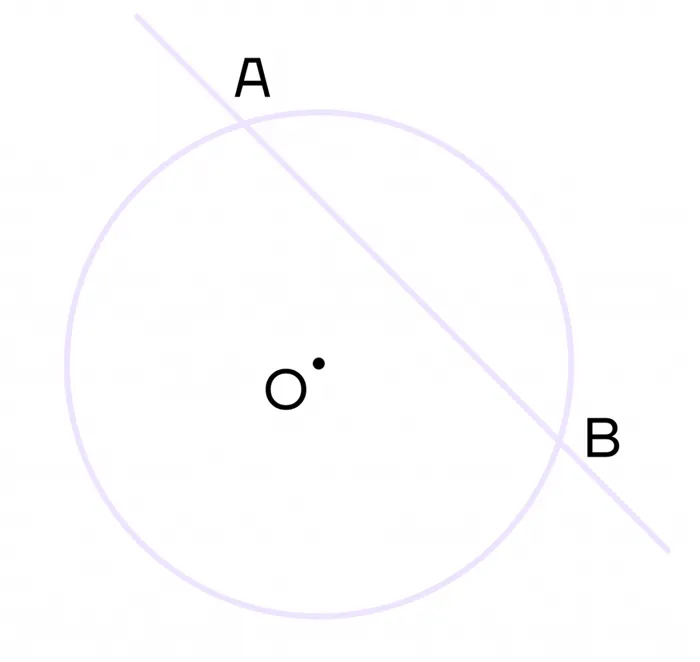
Рассмотрим, как разрезается пицца или пирог. Каждый разрез является вторичным. То есть, он делит круг на разные части.

Свойства секущей

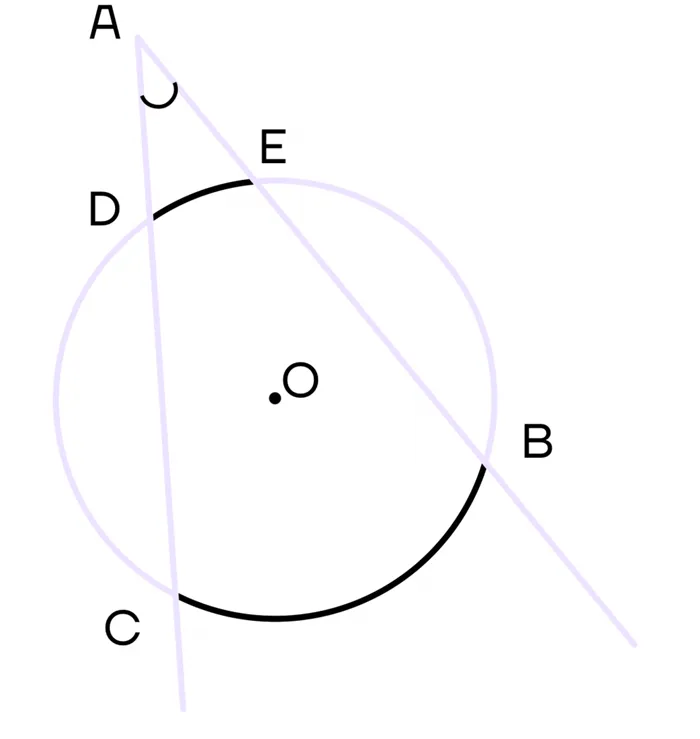
1 Собственность. Если вы спроектируете вторичную и касательную к окружности в одном и том же месте, то площадь касательной будет равна ее внешней вторичной.

Проведите касательную AB и второстепенные улицы из точки A. Предположим, что вторичная пересекает окружность в точках C и E.

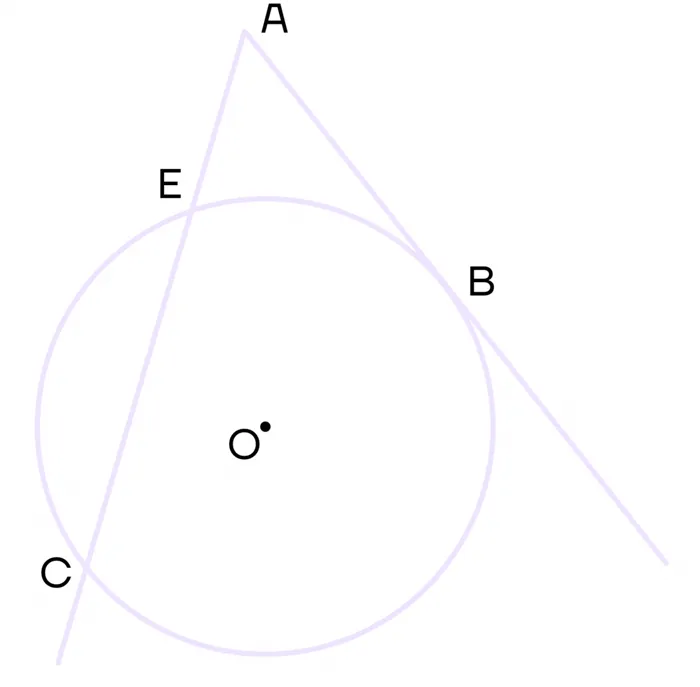
2 Собственность. Если из одной и той же точки провести две вторичные окружности, то произведение первой вторичной вне ее равно произведению второй вторичной вне ее.

Начертите АВ (пересекает окружность в точках Е и В) и Аг (пересекает окружность в точках С и D). Тогда ac * ad = ab * ae.

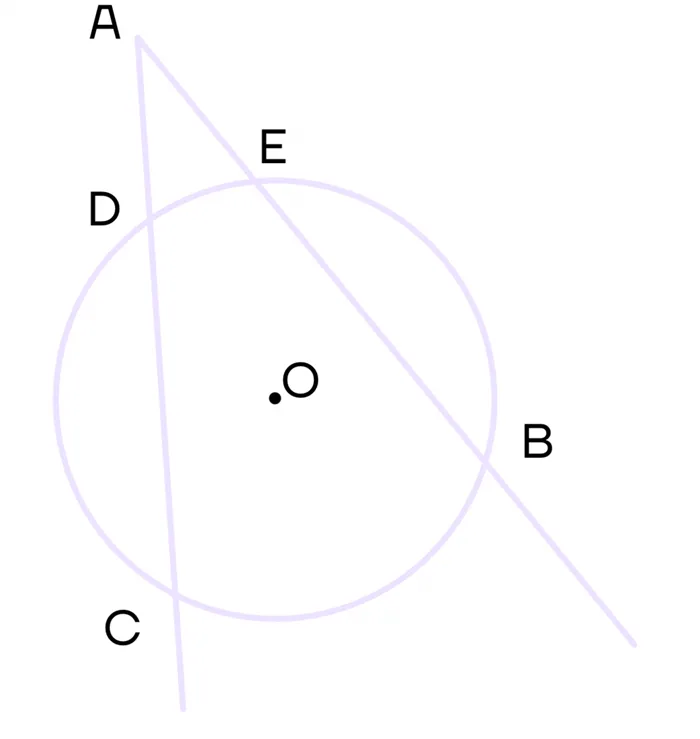
3 Собственность. Угол между двумя вторичками равен половине разницы между измерениями наибольшей и меньшей дуг, заключенных между вторичками.

Предположим, что необходимо найти угол наклона такси. Тогда угол ⌘ (cab = \ frac(⋃cb-⋃de)⌘).

Не бойтесь символа «⋃» — в математике он используется для объявления дуги окружности.

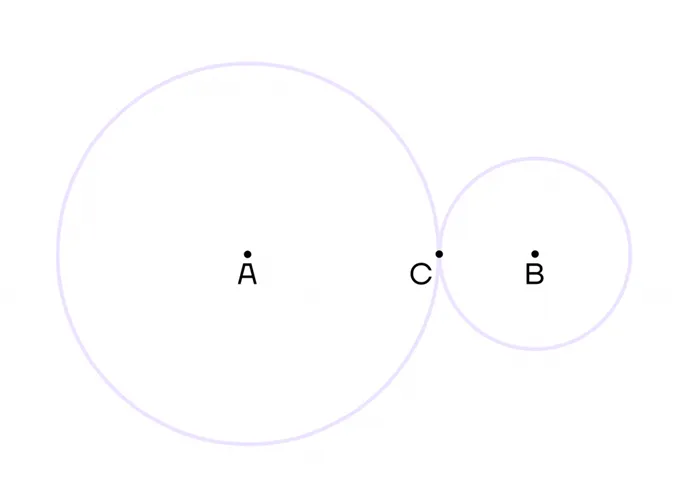
Касание окружностей

Я видел прямую и окружность, касательную к окружности, могут ли две окружности касаться друг друга? Если окружности имеют общую точку, то они касаются друг друга.

И даже есть несколько вариантов такого прикосновения:.

В данном случае точка C является точкой контакта.

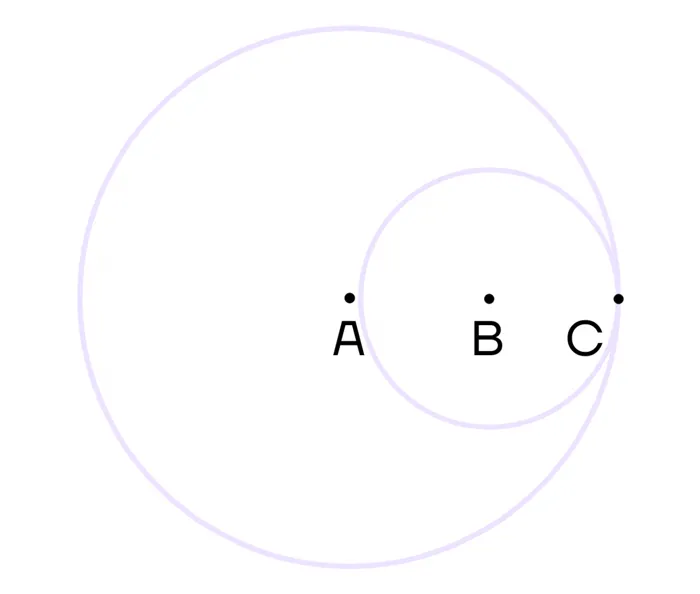
В этом случае точка C также является точкой контакта.

Касательная окружность часто используется в ювелирном дизайне. Это решение позволяет создавать уникальные и очень красивые изображения.

Как уже было определено, круги могут находиться в контакте друг с другом. Однако есть и другой вариант их взаимной договоренности. Круги пересекаются. В этом случае у них есть две общие черты.

Изучите свойства кругов, соприкасающихся друг с другом.

Если провести прямую через центры окружностей A и B, то на этой же прямой образуется точка соприкосновения C.

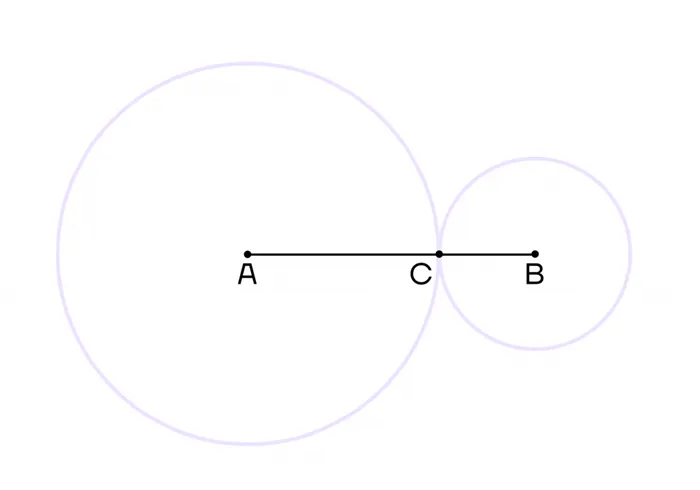
Из этого определения можно вывести существование производной. Если последний имеет значение 0, то схема не имеет ничего общего.

Касательная перпендикулярна радиусу, проведённому в точку касания

Давайте снова посмотрим на приведенную выше диаграмму. Нарисовав радиусы OA и OB, мы видим, что углы OAM и OBM — прямые линии.

Радиусы OAM и OBM перпендикулярны касательной линии.

Этот факт можно использовать в задаче без доказательства.

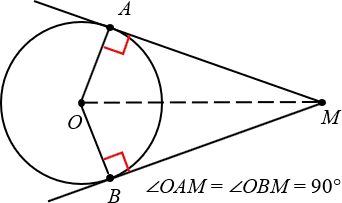
Луч, проведенный из точки касания, перпендикулярен к касательной линии.

Кстати, обратите внимание: при проведении касательной OM получаются два равных треугольника OAM и OBM.

Соотношение между касательной и секущей

Это гораздо более серьезный факт, и большинство студентов его не осознают. Рассмотрим касательные и несовершеннолетние, проходящие через одну общую точку M. Разумеется, вторичка состоит из двух частей. Внутренняя часть круга (часть BC, называемая струной) и внешняя часть круга (внешняя часть, MC).

Произведение всей внешней стороны равно квадрату касательной части

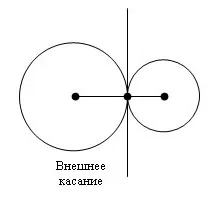
Отношение минора к тангенсу.

Угол между касательной и хордой

Это более продвинутый факт, который часто используется для решения сложных проблем. Настоятельно рекомендуется принять это во внимание.

Угол между касательной и струной равен углу окружности на этой струне.

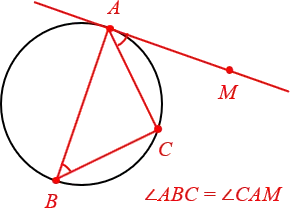
Откуда берется точка Б? В реальной проблеме она обычно «всплывает» где-то в ситуации. Поэтому важно научиться распознавать этот узор на рисунке.

Иногда это обидно:)

Уровень знания геометрии можно определить по древним рукописям, посвященным математике. Они похожи на учебники или, точнее, задачники, в которых даются решения различных практических задач.

Примеры решения

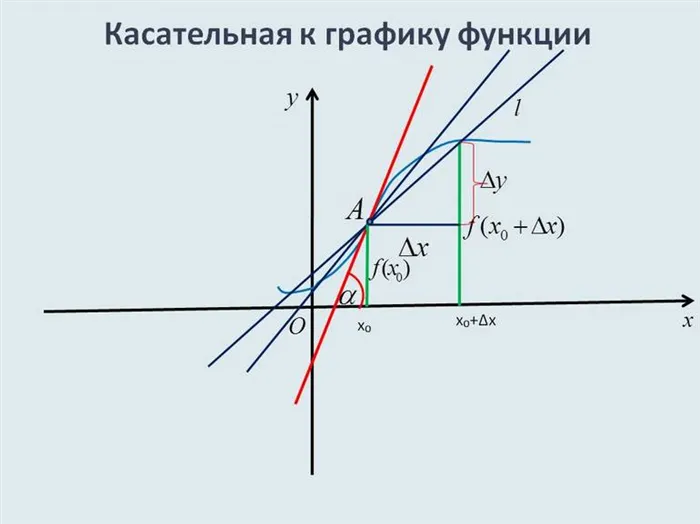
Нахождение уравнения линии, касательной к определенному графику функции, связано с различными проблемами. Самой простой является проблема следующего представления Линия является касательной к графику функции. Найдите все контактные точки. В этом случае даны уравнения функции и график линии. Некоторые задачи считаются более сложными. Они предполагают написание уравнений одной или нескольких касательных линий.

Упражнения и ход вычислений

Требуется написать уравнение прямой от y(x) = x ^ 3-2x ^ 2+3 до ho = 2. Следует использовать следующий алгоритм:.

Значение в х0 = 1: y(2) = 2 * 2^2 — 3 * 2 + 1 = 3.
Производная в заданной точке: y'(2) = 4x — 3 = 5.
Подстановка: y = y(2) + y'(2) * (x — x0) = 3 + 5(x — 2) = 3 + 5x — 10 = 5x — 7.

Один из типов задач — найти точку на волге, где прямая (касательная)||| корова. Дана функция f(x) = x ^ 3-x ^ 2 —3x + 7. Угол наклона равен 0 градусов из-за касательной линии|||. OX (производная в точке касания равна 0).

Алгоритм решения следующий.

Найти производную исходной функции: f'(x) = 3x^2 — 2x — 3.
Если приравнять выражение к 0, то получится обычное квадратное уравнение: 3x^2 — 2x — 3 = 0.
Дискриминант: D = b^2 — 4ac = 4 — 4 * 3 * (-3) = 40.
Уравнение имеет 2 корня: х1 = (2 — sqr(40)) / 6 = (1 — sqr(10)) / 3 и x2 = (1 + sqr(10)) / 3.

Из-за ошибок при вычислении кубических корней рекомендуется оставить их как есть. В этих примерах нет необходимости рисовать график.

Поэтому среднее геометрическое уравнения касательной к функции является производной. Следует изучить основные понятия, типы и решения стандартных задач. Также необходимо повторить дифференциальную таблицу функций.

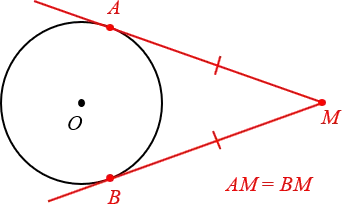
Еще раз сформулируйте свойства касательной, исходящей из точки. Касательные, проведенные из точки на окружности, равны и образуют угол, равный прямой, проходящей через эту точку и центр окружности.

Равенство отрезков касательных

Задавались ли вы когда-нибудь вопросом: «Сколько отрезков касательных можно провести из точки на окружности?». Вот, представьте себе, всего два! Например:.

И еще более удивительный факт заключается в следующем.

Отрезки касательных, проведенных из точки на окружности, равны.

Другими словами, на этой диаграмме ߡ (ߡ displaystyle AB = AC \).

Самым важным в этом факте является то, что радиус точки касания перпендикулярен к линии касания.

Нарисуем лучи ⌘ (⌘ displaystyle OB \) и ఫ (⌘ displaystyle OC \) и соединим лучи ⌘ (⌘ displaystyle O \) и ఫ (⌘ displaystyle A \).

\(⌘ displaystyle AB \), потому что это касательная линия, и ߋ(⌘ displaystyle OB \ bot AB \), потому что это касательная линия. Также, 슰 (슰 displaystyle OC \ bot AC \).

Существуют два прямоугольных треугольника \(⌘ displaystyle AOB \) и \(⌘ displaystyle AOC \), которые являются

(ищите «прямоугольный треугольник», если вы не помните, когда прямоугольные треугольники равны).

Однако, поскольку ɑ (ɑ displaystyle \ Delta AOB = \ Delta AOC, ɑ), мы имеем ɑ (ɑ displaystyle AB = AC \). УРА!

И опять же — этот факт также очень важен: у

Касательные, проведенные из одной точки, равны.

Есть еще один факт, который мы не будем здесь доказывать, но который может помочь решить эту проблему.

Для каждой прямой ǫ (ǫ displaystyle AD \), пересекающей окружность, ǫ (ǫ displaystyle AD \ cdot AC = A ^> \), где ǫ (ǫ displaystyle AB \) — отрезок касательной.

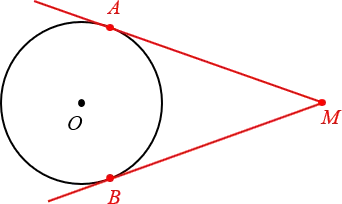
Умный способ выразить это заключается в следующем:.

Квадрат длины касательного отрезка равен произведению минимумов его внешних отрезков».

При решении задачи необходимо учитывать особые случаи. Вам нужно вычислить уравнение прямой линии или найти точку касания с окружностью, эллипсом, преувеличением или параболой. Очень распространенная проблема также встречается у инженеров с ременной передачей.

Касательная к окружности

В этом уроке повторяются три случая размещения окружностей и линий в соответствии с отношением расстояния от центра окружности до линии к радиусу окружности. Подробно ответьте, равно ли расстояние от центра окружности до прямой радиусу окружности. Введите понятие «касательная» к окружности и «точка соприкосновения». Рассмотрите свойства и знак касательной к окружности. Изучите касательные к окружности, проведенные из точки, и их свойства.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный кабинет.

Конспект урока «Касательная к окружности»

Вспомните, как окружности и линии могут быть расположены в соответствии с соотношением между расстоянием от центра окружности до линии и радиусом окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности, вспомните, что у прямой и окружности есть две общие черты.

Если расстояние от центра окружности до прямой равно радиусу окружности, то у прямой и окружности есть только одна общая черта.

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Сегодня мы обсудим особый случай, когда прямая и окружность имеют общую точку. Такая линия называется касательной к окружности. Точки, общие для прямой и окружности, называются точками касательной к прямой и окружности.

Покажите точки касания окружности и дайте этим точкам название касательной.

Точки b и d являются касательными к окружности, а C и F — точками соприкосновения.

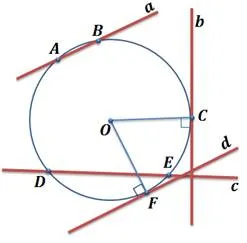
Затем проведите радиус от центра окружности до точки касания. Из рисунка видно, что лучи должны быть перпендикулярны точкам касания.

Давайте докажем или опровергнем эту гипотезу.

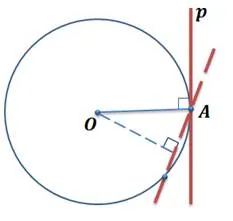
Предположим, что луч p является касательной к окружности с центром O и точка A является точкой касания.

Предположим, что касательная линия p не перпендикулярна радиусу O. В этом случае радиус O является касательной к линии p. Из точки O к линии p опускается перпендикулярная прямая. Расстояние от O до p меньше радиуса, потому что перпендикулярная линия из O меньше любого наклона из O. Это означает, что прямая и окружность пересекаются в двух точках. Но тогда линия p — это боковая линия и, по условию, она является касательной.

Поэтому гипотеза о том, что линия касания не перпендикулярна радиусу, проведенному в точке касания, не подтверждается.

Таким образом, мы доказали свойство касательных к окружности. Давайте сформулируем это следующим образом:

Теорема (свойство касательной). Касательная линия окружности перпендикулярна радиусу, заданному точкой касания.

Задача. Радиус делит хорду , параллельна хорде

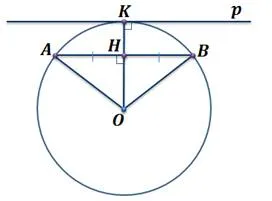
Создайте окружность, нарисуйте нить AB и нарисуйте радиус OK, который делит нить AB на две части. Проведите касательную к окружности в точке K.

Начертите радиусы AB и OB и рассмотрите равнобедренный треугольник AOB. O делит AB на 2, поэтому OH — медиана и высота. Это означает, что OH перпендикулярна AB. Согласно свойству касательной, линия касания, проведенная через точку K, перпендикулярна OG. Таким образом, существуют две прямые, перпендикулярные радиусу OC.

Это нужно было доказать.

Теперь рассмотрим две касательные к окружности, центр которой O проходит через точку A и является касательной к окружности в точках B и C. Отрезки AB и AC называются касательными, проходящими через точку A. Эти секции обладают следующими свойствами

Теорема. Отрезки касательных равны, если они исходят из одной точки и образуют угол, равный прямой, проходящей через эту точку и центр окружности.