Например, каждый ученик должен уметь понимать определения вертикальных и средних по высоте и высоте перегородок. Они также должны знать основные свойства.
Построение треугольника по трем элементам
Строительные проблемы распространены в геометрической прогрессии. Суть этих задач заключается в следующем При определенных начальных условиях необходимо построить тот или иной геометрический объект с помощью линейки и компаса. Рассмотрим общий принцип решения этих задач.
Анализ проблемы. На этом этапе необходимо определить взаимосвязь между данными и проектируемым объектом. Результатом этого этапа является план решения поставленной задачи.
Строительство. В соответствии с разработанным планом осуществляется строительство объекта.
Доказательство. На этом этапе вам необходимо доказать, что изображенная на диаграмме фигура полностью удовлетворяет заданным условиям.
Вам трудно решить проблему самостоятельно?
Обратитесь за помощью к своему учителю.
Инспекция. На этом этапе анализируются и находятся начальные условия, при которых задача может быть решена одним из способов. Эта проблема может решаться двумя способами, а может и не решаться вовсе.
Проанализируйте задачу построения треугольника с использованием трех различных начальных условий.
Изображение треугольника, если задана одна сторона и два прилегающих к ней угла
Дан треугольник с одной стороной ˉ (bc \) и прилежащими углами ˉ (∝ \) и ˉ (b), постройте треугольник.
Проанализируйте условие 1. Требуется построить треугольник ǫ (abc \) с одной стороной ǫ (bc \) и углом ǫ (∠K= ∝ и ρm= βǫ). Нарисуйте план решения проблемы.
- Начертим прямую a, а на ней отмерим отрезок \(BC\) ;
- Изображаем угол \(∠K= ∝\) с центром в вершине \(B\) на стороне \(BC\) ;
- Изображаем угол \(∠M= β\) с центром в вершине \(C\) на стороне \(BC\) ;
- На пересечении лучей построенных углов получим точку \(A\), соединяем ее с точками \(C\) и \(B\), получаем отрезки \(AC\) и \(AB\) .

3. доказательство. Исходя из иллюстрированной формы, сделайте вывод, что все заданные условия полностью удовлетворены.
4. экзамен. Каждый из указанных углов может быть произведен в обратном направлении, но при этом может быть построен другой треугольник, но точно такой же, как и первый, поэтому можно предположить, что решение этой задачи уникально. Сумма всех углов треугольника должна быть равна 180 0. Поэтому, если сумма ɛ (∝ \) и ɛ (b \) больше 180 0, то решение задачи невозможно.
Изображение треугольника, если заданы три стороны
Даны три стороны треугольника ɑ (ab \), ɑ (ac \) и ɑ (bc \), требуется построить треугольник.
1. проанализируйте условия. Используя три стороны (ab \), ⌘ (ac \) и bc, постройте треугольник ⌘ (abc \). Разработайте план решения проблемы.
- Начертим прямую \(a\), а на ней отмерим отрезок \(AB\) ;
- Чертим с помощью циркуля две окружности. Одна окружность будет с центром в точке \(A\) с радиусом \(AC\), а вторая с центром в точке \(B\) с радиусом \(BC\) ;
- На пересечении окружностей мы получим точку \(C\), соединяем ее с точками \(A\) и \(B\), получаем отрезки \(AC\) и \(BC\) .
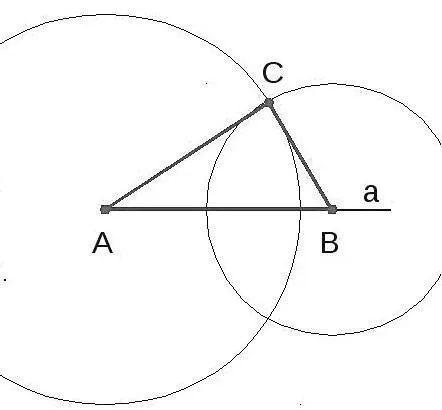
3. доказательство. Исходя из иллюстрированной формы, сделайте вывод, что все заданные условия полностью удовлетворены.
Просто напишите, и мы вам поможем.
4. исследование. Поскольку построенная окружность имеет два пересечения, мы можем построить еще один треугольник, но поскольку он точно такой же, как и первый, можно предположить, что решение этой задачи уникально. Поскольку сумма двух сторон треугольника всегда больше его третьей стороны, можно сделать вывод, что задача не имеет решения, если это условие не выполняется на данной стороне.
Согласно принципу равенства треугольников по одной стороне и парам углов, примыкающих к ней, нарисованный треугольник равен всем треугольникам из этих элементов.
Равносторонний треугольник. Свойства.
Это естественно, не так ли? В совокупности каждый из трех равных углов равен.
| Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!). |
Почему бы и нет? Что ж, давайте рассмотрим равносторонние треугольники.
| Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный. |
Таким образом, каждая высота равностороннего треугольника также является биссектрисой, медианой и срединным перпендикуляром! Как и в обычных треугольниках, в равностороннем треугольнике нет особых линий, только три!
| Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан. |
| Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. |
Поскольку это происходит, теперь это должно быть очевидно.
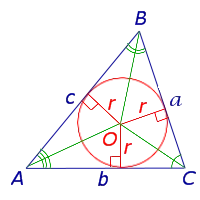
Посмотрите на диаграмму: точка — центр треугольника. Таким образом, радиус пограничного цикла (обозначается ), а — радиус внутриклеточного (символический).
Но точки также являются прерывистыми пересечениями! Напомним, что медиана отделяется от точки пересечения, измеренной сверху.
| Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны. |
Давайте проверим это.
Равносторонний треугольник. Высота
Подумайте — это прямоугольник.
Равносторонний треугольник. Радиус описанной окружности
Мы уже выяснили, что эта точка является не только центром периметра, но и центральной точкой пересечения. Хорошо.
Мы уже обнаружили его ценность. Сейчас мы его заменяем:.
Равносторонний треугольник. Радиус вписанной окружности
С этого момента все должно стать предельно ясно.
Сейчас обсуждаются все основы. Конечно, можно задать сотни вопросов о длинах различных частей равностороннего треугольника.
Но главное, что нужно помнить при решении вопросов о равносторонних треугольниках, это то, что все его углы известны как равные, а все высоты — как биссектрисы, промежуточные и перпендикулярные.
Определение 1. Биссектриса угла — это радиус, который делит угол на две равные части.
Теорема 1 (Основные свойства частей угла). Каждая часть угла находится на одинаковом расстоянии от стороны угла (рис. 1).
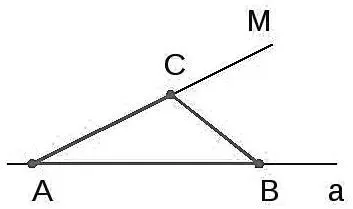
ДОКАЗАТЕЛЬСТВА Рассмотрим любую точку D в укусе вактора и проведем вертикали DE и DF от D до края угла (рис. 1). Прямоугольные треугольники ADF и ADE равны, так как имеют равные углы DAF и DAE, а подчиненные объявления являются общими. Следовательно.
Необходим для доказательства.
Теорема 2 (обратная теорема теоремы 1). Если точки находятся на одинаковом расстоянии от сторон угла, то он лежит на биссектрисе угла (рис. 2).
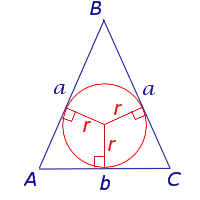
Доказательство Рассмотрим любую точку D в углу BAC. Он находится на одинаковом расстоянии от края угла. Проведите перпендикуляры DE и DF из D перпендикулярно к краю угла (рис. 2). Прямоугольные треугольники ADF и ADE равны, так как имеют равные DF и DF, а нижний AD является общим. Следовательно.
Необходим для доказательства.
Определение 2. Окружность называется зарегистрированной под углом, если она является касательной к стороне угла.
Теорема 3. Если окружность зарегистрирована под углом, то расстояние от вершины угла до точки касания окружности со стороной угла равно.
Доказательство Пусть d будет записано на углу BAC, а e и f — это e и f вместе с боковыми линиями (рис. 3).
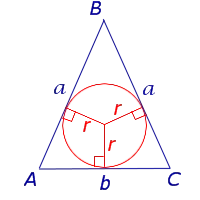
Прямоугольные треугольники ADF и ADE равны, потому что у них равные кривые DF и DF (лучи окружности — это лучи окружности), а меньший AD — общий. Поэтому.
Необходим для доказательства.
Наблюдение. Теорему 3 можно сформулировать и по-другому: из одной точки в другую части касательных линий, проведенных через окружность, равны.
Определение 3. Биссектриса треугольника — это часть угла треугольника, соединяющая верхнюю часть треугольника с противоположной точкой.
Теорема 4. В каждом треугольнике три биссектрисы пересекаются в одной точке.
Доказательство Рассматриваются два ABCS A и C, символизирующие перекресток (рис. 4).
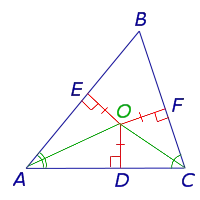
Из O оставьте перпендикуляры OD, OE и стороны треугольника. Так как O лежит на биссектрисе бьющего, равенство справедливо согласно Теореме 1.
Равенство верно, так как точка o лежит на биссектрисе угла ACB согласно Теореме 1.
Следовательно, верно равенство: o — биссектриса угла ACB.
Поэтому из Теоремы 2 следует, что данная точка лежит на биссектрисе угла ABC. Следовательно, все три биссектрисы треугольника проходят через одну точку и должны быть доказаны
Определение 4. Окружность, зарегистрированная в треугольнике, — это окружность, которая касается всех сторон треугольника (рис. 5). В этом случае треугольник называется периферийным треугольником вокруг периферии.
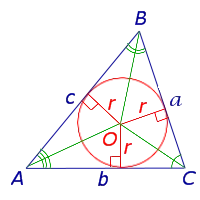
Впоследствии. Можно зарегистрировать круг в любом треугольнике, но только в одном. Центр окружности, записанной в треугольнике, — это точка пересечения всех сторон треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Полезно представить типы окружностей, зарегистрированных в треугольниках, в следующей таблице, где указаны радиусы окружностей.
a, b и c — стороны треугольника, s — площадь, r — радиус коциркуля, p — полуокружность.
a — сторона равностороннего треугольника, r — внутренний радиус.
где a, b, c — стороны треугольника, s — площадь, r — эндогенный радиус и p — полуреверс.
Где a, b и c — стороны треугольника, r — внутриклеточный радиус, а p — полупинеометр.
Равнобедренный треугольник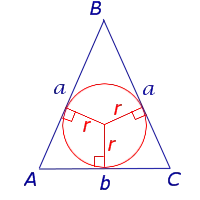 Равносторонний треугольник
Равносторонний треугольник
Где a — сторона правильного треугольника, r — внутриклеточный радиус
Прямоугольный треугольник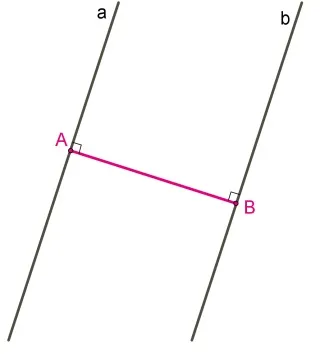
где a, b, c — стороны треугольника, s — площадь, r — эндогенный радиус и p — полуреверс.
Где a, b и c — стороны треугольника, r — внутриклеточный радиус, а p — полупинеометр.
Равнобедренный треугольник Равносторонний треугольник
Равносторонний треугольник
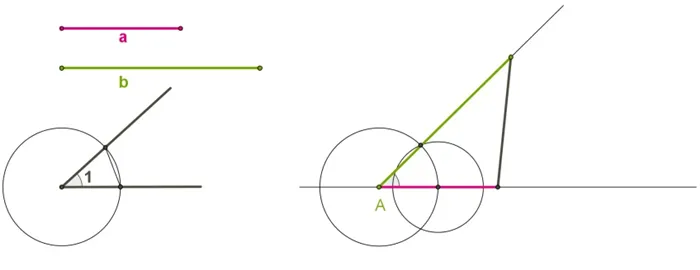
Где a — сторона правильного треугольника, r — внутриклеточный радиус
Прямоугольный треугольник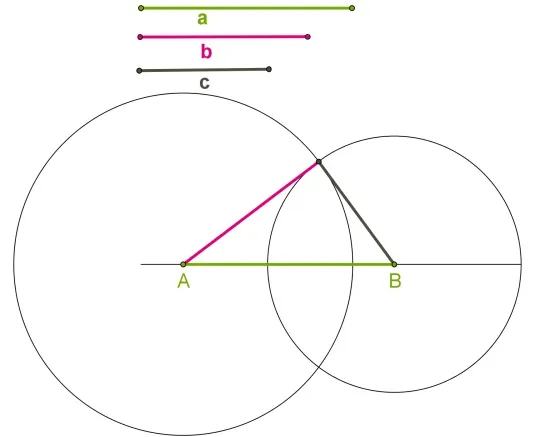
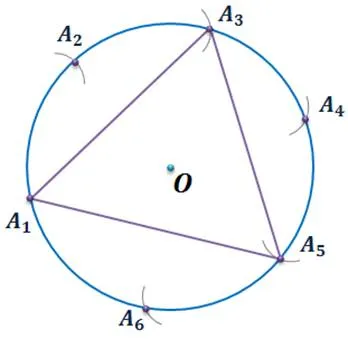
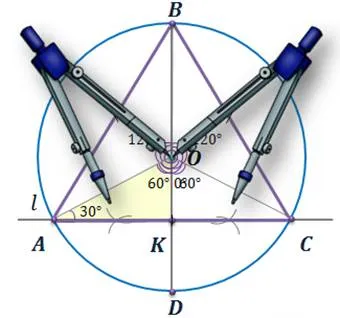
Даже круг с центром О, используя пилу, равную радиусу, начинают гравировку от одной точки круга до последнего гравировального знака, совпадающего с первоначально взятой точкой. Соединив эти точки в одну, вы получите прямоугольный треугольник.
Как построить треугольник по трем элементам с помощью циркуля
Используя компас, можно изобразить треугольник с тремя известными элементами. Например, есть три аспекта в виде частей MC, OE и FG, для которых необходимо построить треугольник ABC. Должны быть выполнены следующие условия:.
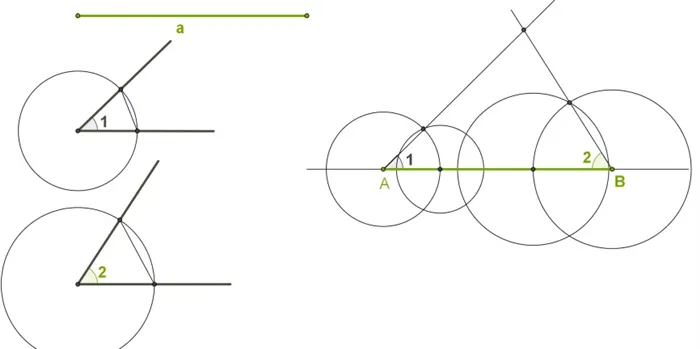
Используя линейку, проведите прямую линию a. Используя компас, проведите линию AB, соответствующую отрезку MK. В этой процедуре вы можете отметить точку A на линии A. После измерения сечения компаса MK необходимо начертить окружность с радиусом, равным центру A и MK. Не нужно рисовать весь цикл, а только лук, как показано на рисунке. Точка пересечения окружности с линией A — b.
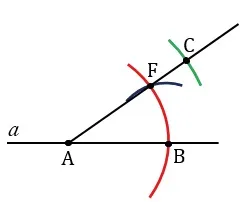
Измерьте сечение OE с помощью компаса и начертите окружность, центр которой совпадает с точкой A, а радиус соответствует сечению OE. На изображении бант выделен синим цветом.
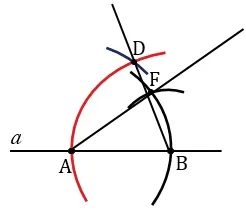
Следующий шаг — с помощью компаса измерить сечение FG и нарисовать окружность. Центр этого цикла совпадает с точкой B, а его радиус соответствует прямому участку FG. На рисунке лук обозначен зеленым цветом.
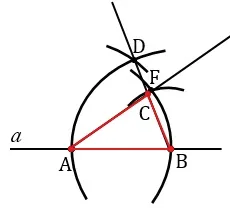
Точки, в которых центры A и B и окружность с лучами OE и FG определяются как C, удобно соединять с помощью линейки. В результате получается геометрическая фигура в виде треугольника ABC.
Если условия задания выполнены, то нарисованный треугольник является искомым треугольником.
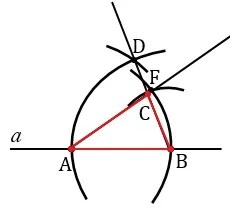
Важно отметить, что такие задания не имеют решения во всех случаях. Причина в том, что неравенство треугольника должно выполняться для каждого треугольника. То есть, для каждого треугольника сумма двух сторон больше третьей стороны. Если один из отрезков, обозначенных условно, больше суммы двух других, то построить треугольник со сторонами, соответствующими этим отрезкам, невозможно.
Треугольники можно построить с помощью компаса и углов между ними, если известны обе стороны. Например, существуют секции MK и OE и углы HK. Треугольник ABC должен быть построен следующим образом.
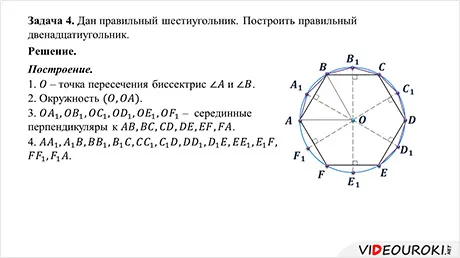
Решение задач на построение треугольника по трем элементам
Существует несколько сторон треугольника BC, в которых соприкасаются углы ߋ альфа и окклюзия. Необходимо построить треугольник из трех известных элементов.
Предположим, что углы треугольника ABC соответствуют следующим условиям
План действий может быть составлен по стандартному алгоритму.
- Построить прямую а и отмерить на ней отрезок ВС.
- Начертить угол К с вершиной В на стороне ВС.
- Изобразить угол М с вершиной С на стороне ВС.
- На пересечении лучей изображенных углов получить точку А, соединить ее с точками С и В для получения отрезков АС и АВ.
В процессе доказательства рассмотрим изображение треугольника. Можно сделать вывод, что данные условия соблюдены. Указанный угол также можно провести в обратном направлении, поэтому второй треугольник можно изобразить соответствующим образом. Однако из-за сходства с первым можно сделать вывод, что существует только одно решение проблемы. Если углы ዄ alpha и ዅ b равны более 180 градусов, то задача не имеет решения.
Даны три стороны треугольника AB, AC и BC. Треугольник должен быть построен.
Проанализировав условия проблемы, можно создать план решения.
- Начертить прямую а и отметить на ней отрезок АВ.
- Используя циркуль, изобразить пару окружностей. Одна из них имеет радиус АС и центр в точке А, а вторая — радиус ВС и центр в точке В.
- Точку, где пересекаются данные окружности, можно обозначить С. Далее следует соединить точку С с точками А и В. В результате получаются отрезки АС и ВС.
- Затем остается построить треугольник.
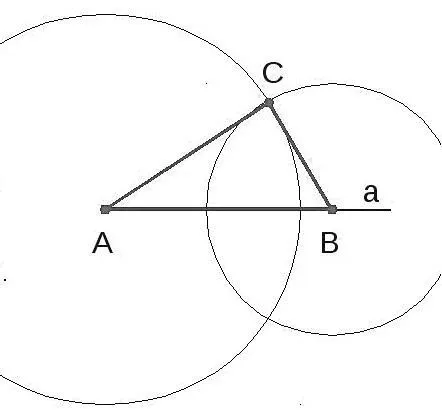
Полученная геометрия соответствует условиям задачи. Нарисованная окружность имеет два пересечения, которые могут создать еще один треугольник. Как и в первом случае, проблема имеет единственное решение. Поскольку сумма сторон треугольника всегда больше его третьей стороны, задача не имеет решения, если это условие не выполняется на этих сторонах.
Треугольник имеет две стороны AB и AC и угол ⌘alpha между ними. Треугольник должен быть спроектирован.
Процедура выполняется следующим образом.
- начертить прямую а, отметить отрезок АВ;
- отмерить угол МАВ, соответствующий углу \alpha;
- отложить отрезок АС на прямой АМ;
- начертить третью сторону треугольника СВ, соединив точки В и С.
В результате получается треугольник:.
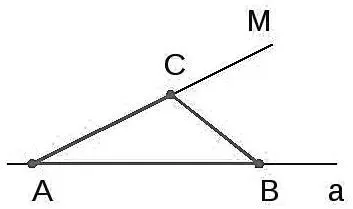
По нарисованной геометрической фигуре можно сделать вывод, что условия работы соблюдены. Ряд A бесконечен. Это позволяет конструировать множество подобных треугольников. Предположив, что все они одинаковы, сделаем вывод, что существует только одно решение проблемы. Если угол ⌘ alpha больше 180 градусов, то задача не имеет ответа, так как сумма всех углов треугольников должна быть равна 180 градусов.
Первое, что нужно сделать, это определить неравенство треугольника, то есть то, что длина отрезка меньше суммы длин двух других частей. Если это условие соблюдено, то допустимо, чтобы эти отрезки были сторонами треугольника.
Построение прямоугольного треугольника
Треугольник с одним прямым углом называется прямоугольным треугольником. Имея катетер и подчиненного, несложно спроектировать прямоугольный треугольник. Он может быть извлечен из катетера и подчинен.
- С помощью линейки чертим гипотенузу заданной длины. Назовем этот отрезок АВ.
- Ставим острие циркуля в точку А и проводим полуокружность, радиус которой немного больше, чем половина отрезка.
- Переставляем острие циркуля в точку В и проводим аналогичное действие. Наши дуги пересекаются в двух места. Соединяем эти точки. Точка пересечения данной линии и отрезка АВ – его середина, точка О.
- С помощью циркуля рисуем окружность, центр которой находится в точке О, а радиус равен отрезку АО.
- Из точки А проводим циркулем дугу, радиус которой равен заданному катету. Точка пересечения дуги и окружности – искомая третья вершина треугольника. Соединяем ее с точками А и В. Задача выполнена.
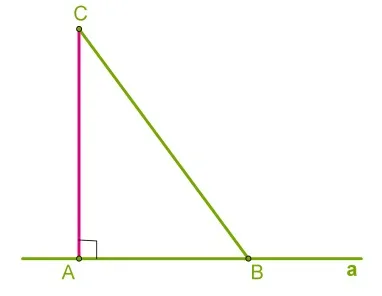
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
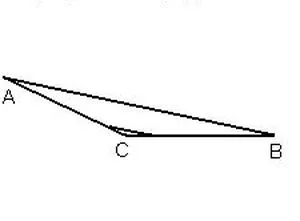
Если один из углов треугольника тупой (больше 90 градусов), он называется тупым треугольником. Чтобы нарисовать тупой треугольник в соответствии с этими параметрами, необходимо
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
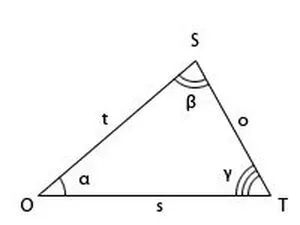
Острые треугольники (все углы меньше 90 градусов) получаются по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.








