Этот метод также может быть использован для сравнения разрезов, спроектированных на земле. Отметьте положение скамьи на равном расстоянии от стены дома. Только в этом случае вместо бумажных полосок нужна доска или веревка.
Как сравнить 2 отрезка: способы решения задачи
Сравнение двух отрезков на уровне — это стандартная работа по геометрии для учеников 7-го класса. Существуют различные способы проведения такого сравнения, каждый из которых подробно описан. Эти виды работ являются элементарными и формируют основу для изучения дальнейшего материала. Как только вы освоите этот простой процесс, в дальнейшем у вас не будет проблем с подобными задачами.
Прежде чем объяснить, как сравнить два раздела, давайте рассмотрим, что такое раздел уровня.
Определение в учебнике по геометрии гласит, что прямой отрезок — это часть линии, ограниченная двумя точками по обе стороны.
Если рассматривать простую прямую, то отрезок — это множество, состоящее из двух различных точек этой прямой (фактически края отрезка) и всех остальных точек между ними (так называемые внутренние точки). ).
Сравнение двух отрезков
Таким образом, в вопросе о том, как сравнить два раздела, можно выделить следующие методы
Если разница положительная, то первый участок больше второго на соответствующее количество единиц. Если результат равен нулю, то отрезки равны. Если ответ — отрицательное число, это означает, что второй отрезок больше первого.

Поэтому мы нашли два способа сравнить эти два раздела. Первый метод показывает, что больше, а что меньше, в то время как второй метод показывает численное значение разницы в длине.
Как сравнить два отрезка: способы и примеры

Некоторые из них являются частью прямой, касательной к двум точкам, которая является кратчайшим расстоянием между этими точками. Существует несколько способов сравнения геометрий, но выбор часто зависит от возможностей, а также от условий задачи. В этой статье описано, как сравнивать секции.
В геометрии две фигуры одинакового размера и формы называются равными. Сравнивая формы, можно понять, одинаковые они или нет. Один из способов сделать это — переплатить. Считается, что предметы равны, если они могут быть покрыты.
Сравнение цифр означает определение того, какая из них больше или меньше. Ответ должен быть однозначным; одна часть не может быть больше другой. В математике такой ответ можно приравнять к отсутствию ответа, поскольку он неверен.
Запишите результаты сравнений с помощью символов больше, меньше и равенства (>, < ,, =). Например, длина отрезка AB равна 2 см, а длина отрезка VG равна 8 см. Результаты сравнения должны быть описаны: ab & lt, vg или vg & gt, ab.
Существует множество способов сравнения ценностей. Выбор зависит от возможностей и условий.
- визуальный способ,
- измерительный,
- сравнение наложением,
- сравнение в координатной сетке.
Лучше всего визуально варьировать длину и смотреть только на них, чтобы понять, какая из двух длиннее. Однако это не всегда так.
Измерение длины
Самый простой способ — это измерение. Для этого просто измерьте длину секции и посмотрите, какая из двух больше. Если у вас нет линейки, но вы проектируете их в квадратных листах, вы можете измерить длину, измеряя квадраты. В одном сантиметре два квадрата. Это метод сравнения с измерениями длины, но есть и способ дублирования сравнения.
Наложение друг на друга
Как насчет дублирования AB и VH:.
- Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
- Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (>, или <,).
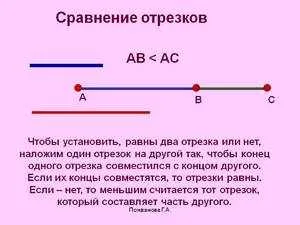
Это может произойти при наложении одной секции на другую, когда ровно половина одной секции выравнивается с другой. Точка, в которой она делится на два равных отрезка, называется средней. А если существует средняя точка B, то AB = BB.
Точно так же можно сравнивать прямые линии, а также другие геометрические фигуры и углы.
Вы можете сделать «линейку» из листа бумаги, и такая линейка не обязательно должна иметь правила, просто отметьте на ней начало и конец одного из отрезков. Затем приложите импровизированную линейку ко второй отметке, совместите первую отметку с первой и сравните положение второй точки относительно конца. Этот метод также можно использовать для сравнения очень больших фигур, например, расстояния между столбиками забора, но при этом рекомендуется использовать не лист бумаги, а кусок веревки.
Если две части могут накладываться друг на друга, они называются равными. Если их можно поставить друг на друга, убедитесь, что один из них больше. Однако это не всегда возможно.
Примеры
Рассмотрите возможность перекрывающихся сравнений. Есть две секции, AB и VG.
Чтобы проверить, равны ли они, соедините их друг с другом так, чтобы их «начало» находилось в одной и той же точке. Другими словами, совместите точки A и B.
Если окажется, что AB является частью VG, это означает, что она маленькая. Это означает, что AB & lt, VG и перекрытие двух концов детали, они равны.
Далее рассмотрим сравнение секций по измерениям. Используя линейку, рассчитайте длину каждой секции. Например, AB = 2 см и CD = 8 см. 8 >, 2, поэтому CD >, AB больше AB.
В этом уроке вы узнаете, как накладывать и сравнивать геометрические фигуры. В частности, мы рассмотрим, как сравнить два отрезка или два угла с помощью их наложения. Также будут введены термины «центр сечения» и «биссектриса угла».
Как сравнить два отрезка: способы и примеры

Некоторые из них являются частью прямой, касательной к двум точкам, которая является кратчайшим расстоянием между этими точками. Существует несколько способов сравнения геометрий, но выбор часто зависит от возможностей, а также от условий задачи. В этой статье описано, как сравнивать секции.
- Способы сравнения двух отрезков
- Измерение длины
- Наложение друг на друга
- Сравнение в координатной сетке
- Примеры
Способы сравнения двух отрезков
В геометрии две фигуры одинакового размера и формы называются равными. Сравнивая формы, можно понять, одинаковые они или нет. Один из способов сделать это — переплатить. Считается, что предметы равны, если они могут быть покрыты.
Сравнение цифр означает определение того, какая из них больше или меньше. Ответ должен быть однозначным; одна часть не может быть больше другой. В математике такой ответ можно приравнять к отсутствию ответа, поскольку он неверен.
Запишите результаты сравнений с помощью символов больше, меньше и равенства (>, < ,, =). Например, длина отрезка AB равна 2 см, а длина отрезка VG равна 8 см. Результаты сравнения должны быть описаны: ab & lt, vg или vg & gt, ab.
Это интересно, потому что можно сравнить две линии линии с одинаковой длиной. Как разделить квадратный трином на множитель?
Существует множество способов сравнения ценностей. Выбор зависит от возможностей и условий.
- визуальный способ,
- измерительный,
- сравнение наложением,
- сравнение в координатной сетке.
Лучше всего визуально варьировать длину и смотреть только на них, чтобы понять, какая из двух длиннее. Однако это не всегда так.
Измерение длины
Самый простой способ — это измерение. Для этого просто измерьте длину секции и посмотрите, какая из двух больше. Если у вас нет линейки, но вы проектируете их в квадратных листах, вы можете измерить длину, измеряя квадраты. В одном сантиметре два квадрата. Это метод сравнения с измерениями длины, но есть и способ дублирования сравнения.
Примечание: Каков радиус геометрической фигуры?
Наложение друг на друга
Как насчет дублирования AB и VH:.
- Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
- Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (>, или <,).
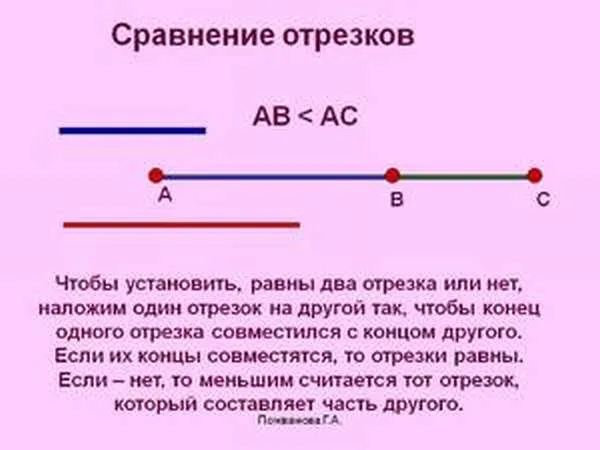
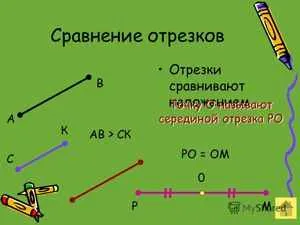
Это может произойти при наложении одной секции на другую, когда ровно половина одной секции выравнивается с другой. Точка, в которой она делится на два равных отрезка, называется средней. А если существует средняя точка B, то AB = BB.
Точно так же можно сравнивать прямые линии, а также другие геометрические фигуры и углы.
Вы можете сделать «линейку» из листа бумаги, и такая линейка не обязательно должна иметь правила, просто отметьте на ней начало и конец одного из отрезков. Затем приложите импровизированную линейку ко второй отметке, совместите первую отметку с первой и сравните положение второй точки относительно конца. Этот метод также можно использовать для сравнения очень больших фигур, например, расстояния между столбиками забора, но при этом рекомендуется использовать не лист бумаги, а кусок веревки.
Если две части могут накладываться друг на друга, они называются равными. Если их можно поставить друг на друга, убедитесь, что один из них больше. Однако это не всегда возможно.
Если у вас есть компас, поместите одну ножку компаса в начало первого участка, а другую — в конец. Затем, не двигая ножки компаса, поместите одну из них в начало второй и посмотрите, находится ли вторая ножка компаса в точке, указывающей на конец. Это то же самое. Если вторая нога находится на прямой линии (первая нога меньше и находится позади), то первая нога больше.
Примеры
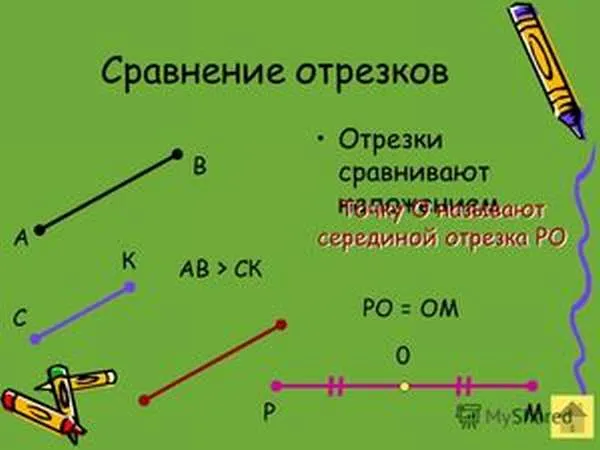
Рассмотрите возможность перекрывающихся сравнений. Есть две секции, AB и VG.
Чтобы проверить, равны ли они, соедините их друг с другом так, чтобы их «начало» находилось в одной и той же точке. Другими словами, совместите точки A и B.
Если окажется, что AB является частью VG, это означает, что она маленькая. Это означает, что AB & lt, VG и перекрытие двух концов детали, они равны.
Далее рассмотрим сравнение секций по измерениям. Используя линейку, рассчитайте длину каждой секции. Например, AB = 2 см и CD = 8 см. 8 >, 2, поэтому CD >, AB больше AB.
Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.
Сравнение отрезков и углов

В этом уроке вы узнаете, как накладывать и сравнивать геометрические фигуры. В частности, мы рассмотрим, как сравнить два отрезка или два угла с помощью их наложения. Также будут введены термины «центр сечения» и «биссектриса угла».
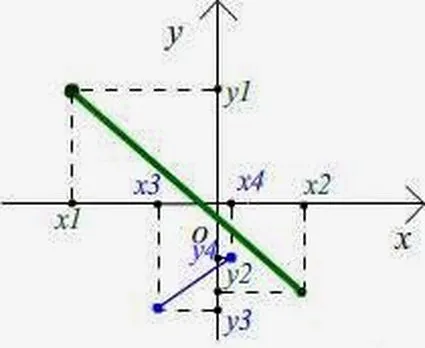
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим обучающим видео в комплекте, вы должны приобрести его в каталоге и добавить в свой личный кабинет.
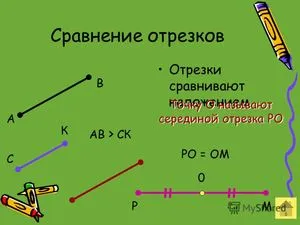
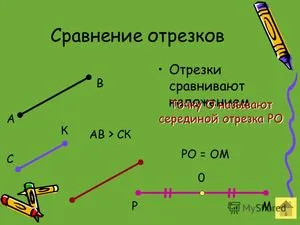
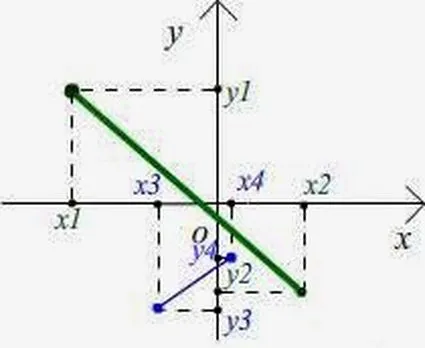
Конспект урока «Сравнение отрезков и углов»
Все вы знаете, что в окружающем нас мире есть предметы, которые имеют одинаковую форму и одинаковые размеры. Например:.

В геометрии две фигуры одинаковой формы и одинаковых размеров называются равными.
Рассмотрим две фигуры, F1 и F2, вырезанные из бумаги. Чтобы проверить, равны ли они, наложите одну фигуру на другую.
Если предположить, что данные выровнены, то можно сказать, что они равны.
Вот некоторые фигуры P1 и P2. Пусть они накладываются друг на друга.
Мы видим, что эти две геометрии не равны, потому что их нельзя причесать.
Вывод: две геометрические фигуры называются равными, если они могут быть помещены в суперпозицию.
Давайте поговорим о том, как сравнить два раздела. Возьмите два произвольных отрезка. Чтобы определить, равны ли они, положите одну секцию на другую так, чтобы концы одной секции совпадали с концами другой. Если два других конца отрезка также выровнены, то отрезки равны.
Затем возьмите отрезки AB и AG и наложите их таким же образом.
Видно, что отрезки не равны, потому что они не идеально выровнены.
Из рисунка также видно, что отрезок АВ составляет часть отрезка АС, поэтому АВ
Изучите раздел AB. Отметьте на нем точку С. Это делит точку C на две равные части.
Поэтому можно сказать, что точка C находится на середине отрезка AB, т.е. AC=CB.
Точка отрезка, которая делит его пополам, то есть на два равных отрезка, называется средней точкой отрезка.
Рассмотрим два неделимых угла.
Чтобы определить, равны ли они, наложите один угол на другой так, чтобы сторона одного угла была совместима с другой стороной, а две другие стороны находились по одну сторону от совместимой стороны. Если две другие стороны также совместимы, то углы идеально совпадают, так что
В нашем случае эти стороны не совместились, следовательно, наши углы не равны, и меньшим является угол, который составляет часть другого, а это угол 1. Запишем это так: угол 1
При использовании невыпуклых углов AOS и развернутых углов BOS наложите их друг на друга способом, описанным выше.
Поскольку угол расширения является частью угла расширения, угол расширения больше угла расширения. Другими словами, угол BOS больше, чем угол AOS.
Обратите внимание, что два развернутых угла, очевидно, равны.
Возьмите угол hk. Проведите из вершины этого угла радиус l и разделите его на два равных угла.
Радиус, который начинается от вершины угла и делит его на два равных угла, называется биссектрисой угла. В этом случае l — биссектриса угла hk.
Сравнивать величины — значит решать, какая из них больше или меньше. Ответ должен быть убедительным. Одна часть не может быть больше другой. В математике такой ответ неверен, его можно считать не имеющим ответа.
Как сравнить два отрезка: способы и примеры

Отрезок — это часть линии, ограниченная двумя точками и являющаяся кратчайшим расстоянием между этими точками. Существует несколько способов сравнения геометрий, но выбор такого метода часто зависит как от возможностей, так и от состояния проблемы. В этом разделе статьи описано, как сравнивать разделы.
В геометрии две фигуры одинакового размера и формы называются равными. Сравнивая формы, можно понять, одинаковые они или нет. Один из способов сделать это — переплатить. Считается, что предметы равны, если они могут быть покрыты.
Сравнение цифр означает определение того, какая из них больше или меньше. Ответ должен быть однозначным; одна часть не может быть больше другой. В математике такой ответ можно приравнять к отсутствию ответа, поскольку он неверен.
Существует множество способов сравнения ценностей. Выбор зависит от возможностей и условий.
- визуальный способ;
- измерительный;
- сравнение наложением;
- сравнение в координатной сетке.
Лучше всего визуально варьировать длину и смотреть только на них, чтобы понять, какая из двух длиннее. Однако это не всегда так.
Измерение длины
Самый простой способ — это измерение. Для этого просто измерьте длину секции и посмотрите, какая из двух больше. Если у вас нет линейки, но вы проектируете их в квадратных листах, вы можете измерить длину, измеряя квадраты. В одном сантиметре два квадрата. Это метод сравнения с измерениями длины, но есть и способ дублирования сравнения.
Примечание: Каков радиус геометрической фигуры?
Наложение друг на друга
Как насчет дублирования AB и VH:.
- Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
- Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> the.<).
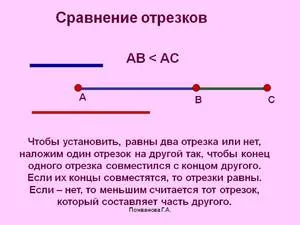
Когда одна секция накладывается на другую, только одна половина может быть выровнена по отношению к другой. Точка, которая делит его на два равных отрезка, называется средней. А если существует средняя точка B, то AB = BB.
Точно так же можно сравнивать прямые линии, а также другие геометрические фигуры и углы.
Вы можете сделать «линейку» из листа бумаги, и такая линейка не обязательно должна иметь правила, просто отметьте на ней начало и конец одного из отрезков. Затем приложите импровизированную линейку ко второй отметке, совместите первую отметку с первой и сравните положение второй точки относительно конца. Этот метод также можно использовать для сравнения очень больших фигур, например, расстояния между столбиками забора, но при этом рекомендуется использовать не лист бумаги, а кусок веревки.
Если две части могут накладываться друг на друга, они называются равными. Если их можно поставить друг на друга, убедитесь, что один из них больше. Однако это не всегда возможно.
Примеры
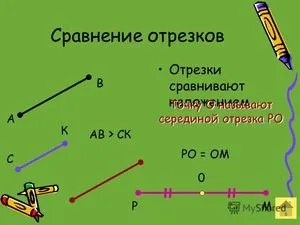
Рассмотрите возможность перекрывающихся сравнений. Есть две секции, AB и VG.
Чтобы проверить, равны ли они, соедините их друг с другом так, чтобы их «начало» находилось в одной и той же точке. Другими словами, совместите точки A и B.
Если AB является частью VG, то она меньше, т.е. AB!< ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.
Далее необходимо измерить и сравнить детали. Используя линейку, рассчитайте длину каждой секции. Например, ab = 2 см, а cd = 8 см. 8> 2, т.е. cd> AB, т.е. cd больше ab.








