Мих дроби в математике могут возникать многими другими способами, например, при сложении неправильных дробей или дробей, или при встрече со смешанными дробями.
Изучение основных правил умножения: как из неправильной дроби сделать правильную
Большая часть математики посвящена работе с дробями или нецелыми числами. Уметь работать с такими числами важно для каждого, так как мы очень часто встречаем их в жизни. Математика — это наука, в которой учащиеся начинают с изучения простых вещей и моделей поведения, а затем переходят к более сложным.
Знание и умение пользоваться такими числами облегчает последующую работу с логарифмами, рациональными экспонентами и интегралами. С этими числами можно делать то же самое, что и с обычными числами. Дроби можно складывать, делить, удалять и умножать. Они также могут быть уменьшены. Работать с дробями очень просто. Главное — знать их основные правила и как их рассчитать.
Основные понятия
Чтобы понять, в чем заключается ценность, нужно представить себе весь предмет. Предположим, у вас есть торт, разрезанный на множество равных кусков или одинаковых ломтиков. Каждая часть называется дробью.
Важно! В случае с дробями, есть целые числа, составленные из равных дробей (отдельных малых чисел).
Например, десятка состоит из пяти двоек, каждая двойка — это дробь от десятки.
Дробные числа имеют названия в зависимости от общего количества целых чисел: десятка может состоять из двух ходиков или пяти двоек. (Необходимо помнить, что (одна треть) равна половине числа, одна треть равна (одной) трети, одна четверть равна (одной четверти). Они также могут казаться разделенными по вертикали — ½, 1/3 или 1/5.
Число, написанное над горизонтальной линией или слева от ее наклона, называется числителем — количеством дробей, взятых от целого числа, а число на линии или справа — знаменателем — целым числом, обозначающим количество дробей, полученных от Например, торт разделен на десять частей, две из которых — недавнего назначения. 2/10 (две половины), т.е. из 10 (знаменателя) берется 2 (числитель) фрагмента.
Фракция.
Что такое дробь, что такое неправильная дробь и что такое нормальная дробь? На эти вопросы можно легко ответить:.
- Обыкновенная – это такая, в котором числитель и знаменатель являются натуральными числами и записываются так: или m/n,
- Правильная дробь – это такая, которая по своей величине меньше единицы, а числитель меньше знаменателя: 5/7 (пять седьмых), 3/5 (три пятых),
- Неправильная – это такая, которая больше или равна единице, а ее знаменатель меньше или равен числителю: 7/5 (семь пятых) или 19/3 (девятнадцать третьих),
- Смешанная – это состоящая из целого и доли: 2 (две целых три пятых) или 5 (пять целых шесть двенадцатых) .
Дробь всегда можно преобразовать в неправильную дробь и наоборот.
Основное свойство гласит: если дробь и делитель делятся и делятся на один и тот же коэффициент, то общее число остается тем же. Это свойство создает все действия с дробями.
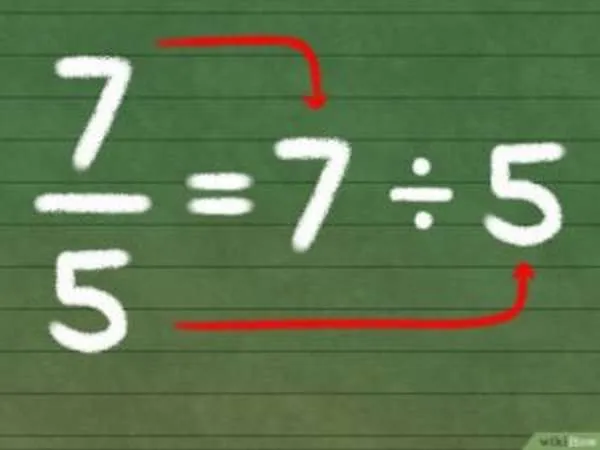
Как преобразовать неправильные дроби в обычные дроби
Это смешно! Игровое обучение математике: как быстро дети могут выучить таблицу умножения.
Как сократить?
Основное правило заключается в том, что уменьшить число дробей можно, разделив числитель и его знаменатель на один и тот же делитель (исключая 0). Это правило гласит, что дроби нельзя уменьшить, уменьшая их.
Пример дробного сокращения: 8/24 сокращается путем деления параметра на 2. Это дает исходное число 4/12. Действие можно повторить, повторно разделив числа: 4:2 = 2 и 12:2 = 6. Вы получаете 2/6. Повторите процедуру еще раз: 2:2 = 1и 6:2 = 3. Параметр уже не может делиться на один и тот же делитель, в результате чего получается 1/3 от неопределенного числа. Каждый уменьшенный номер может быть уменьшен до незарегистрированного номера.
ВАЖНО!!! Если делитель или делители являются выражениями (сначала умножьте каждое выражение на коэффициент, а затем уменьшите выражение на этот коэффициент, создавая сначала дроби.
Их можно уменьшить, умножив дробное выражение между ними: *. Эти числа не могут регистрироваться сами по себе, но могут сокращаться по диагонали, выполняя акт распространения: * = =. Распространение только пересекается: первый числитель со вторым знаменателем и наоборот.
Можно также свести смешанные числа, т.е. целые числа и обычные дроби, к неправильным пропорциям.
- Имея 5, преобразуем его в неправильную дробь. Для этого знаменатель перемножим с его целой частью и приплюсуем к полученной цифре числитель: 5*9+1=46,
- Сумма станет числителем неправильной доли, а его низ позаимствуем от первоначальной,
- В итоге получаем: .
Обратные энергии также применимы. Преобразуйте неправильные дроби в смешанные дроби. Для этого рассмотрите следующие обратные действия.
- Разделим между собой верх и низ: 46:9=5,111111111111111,
- Целый результат деления станет полной цифрой, а бесконечный остаток – верхом доли,
- Знаменатель при этом останется неизмененным,
- Получаем 5 .
Таким образом, фракции могут быть уменьшены любым действием. Умножая их на один и тот же коэффициент и переходя от смешанных дробей к дробям, вы можете уменьшить делитель и цену этого делителя.

Сократите дробь
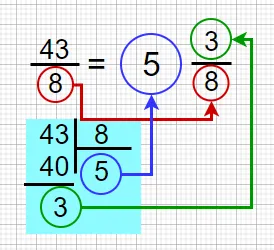
После деления столбиком у нас появились неполное частное, его записываем в целую часть дроби. Остаток записываем в числитель, а делитель записываем в знаменатель.
3 типа дробей
Дроби.
Верхнее число является числителем и указывает на количество деталей.
Меньшее число является знаменателем и указывает на количество делимых частей.
Неправильные дроби и смешанные числа
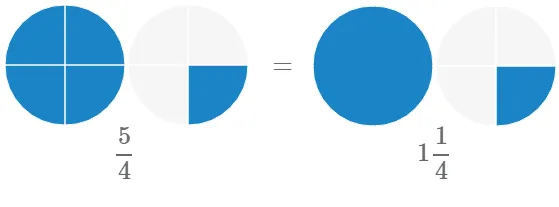
Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа
Поэтому существует два способа преобразования дробей. Классический метод и метод разделения. Необходимость использования двух зависит от конкретного примера. Если перевод окажется проблематичным, всегда можно воспользоваться программой автоматического расчета.
Неправильная дробь
Неправильная дробь — это дробь, у которой числитель больше знаменателя. Она называется неправильной дробью, потому что больше единицы. Дробь можно измерить по тем же правилам, которые применяются к обычным дробям.
Неправильные дроби не могут быть преобразованы в нормальные. Это две разные категории чисел. Поскольку невозможно перевести положительное число в отрицательное, так как одно больше нуля, а другое меньше.
Перевод одного числа в другое означает изменение записи числа без изменения его истинного значения. Чтобы проверить, не было ли число изменено на простом примере, сначала можно поменять число до преобразования, а затем — после преобразования. Результаты должны быть одинаковыми.
Неправильные дроби могут быть преобразованы.
Смешанное число
Смешанное число — это число, состоящее из одной части и двух частей целого числа. Для неправильных дробей целое число удаляется и получается аналогичное значение. Смешанные дроби нельзя умножать, их очень трудно складывать и отнимать.
Неправильные дроби можно превратить в смешанные числа, но все вычисления производятся, и результат должен быть красивым. Для вычисления смешанные дроби сначала преобразуются в неправильные, затем вычисляется целое и снова распределяется.
Целые числа могут быть записаны в виде дробей, как, например, одна восьмая часть от 40 (40:8 = 5). Помните, что дроби — это деления. Умножьте целое число на знаменатель, чтобы получить число 40. Теперь нам остается только сложить две дроби с одинаковым знаменателем.
Смешанные дроби или смешанные числа.
Мих дроби в математике могут возникать многими другими способами, например, при сложении неправильных дробей или дробей, или при встрече со смешанными дробями.
Рассмотрим нерегулярную дробь dž (dž frac).
Поскольку дробные строки являются делениями, 21 x 9 делится на столбцы.
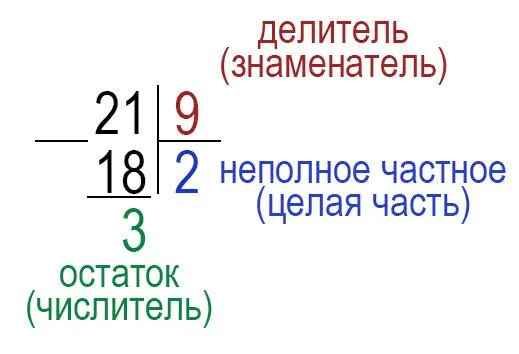
После деления на столбики берется неполная дробь и записывается в целой части дроби. Запишите остаток в числителе, а делитель в знаменателе.
Существуют дроби \(2 \ frac \), которые называются смешанными дробями. В этих смешанных дробях 2 — целое число, а ᢙ (ᢙ frac) — нормальная дробь.
Смешанные дроби состоят из целой части и дробной части.
Рассмотрим другую нерегулярную фракцию \(Ј frac \)
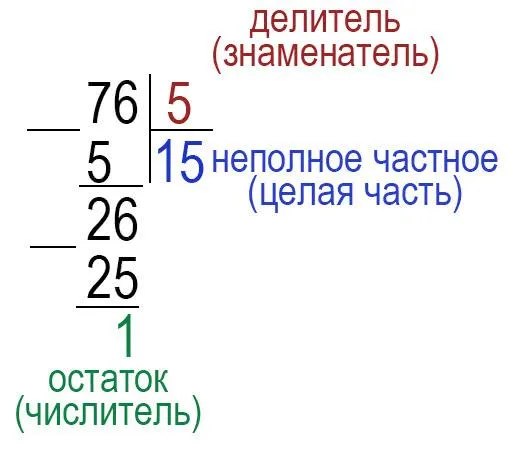
Мы получили смешанную фракцию \(15 \ frac \).
Как смешанную дробь перевести в неправильную дробь?
Чтобы преобразовать смешанную дробь в неправильную дробь, умножьте знаменатель на целую часть и прибавьте ее к числителю, чтобы получить числитель неправильной дроби. Знаменатель остается неизменным. Рассмотрим следующий пример.
Тематический вопрос: могут ли смешанные дроби быть меньше 1? ОТВЕТ: нет. Это связано с тем, что смешанные дроби могут быть выражены как неправильные дроби, а неправильные дроби всегда больше или равны 1.
Что представляет собой целая часть смешанной дроби? Ответ: Целое число указывает на количество полных знаменателей в дроби.
Как смешанные числа представляются в виде неправильных дробей? Ответ: Числитель прибавляется к произведению числителя и целой части, чтобы получить числитель неправильной дроби. Знаменатель не изменяется.
Как можно преобразовать неправильные дроби в смешанные числа? И как разделить целое? ОТВЕТ: разделите числитель на знаменатель. Неполные дроби — это целые числа, делитель — знаменатель, а остаток — числитель. См. пример выше.
Что такое смешанная дробь или смешанное число? ОТВЕТ: смешанная дробь — это число, состоящее из целой и дробной частей.
Пример 1: Считайте дробь смешанным числом: \ (\ frac \).
Решение: разделите дробь на столбец: ɑ (ɑ ɑ ɑ ɑ)
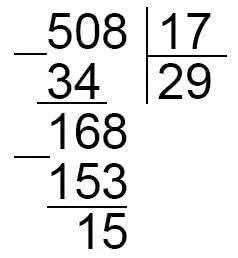
Решение: существует смешанная дробь \(29 \ frac \).
Пример 2: Представьте числа в виде неправильных дробей: а) \(9 \ frac \), б) \(1 \ frac \) Решение: а) \(9 frac = \ frac = \ frac \\\\\) б ) \(1 frac = \ frac = \ frac \\\\\)
Вопрос 1: Масса готовился к экзамену. За один месяц он решил 120 задач. За первую неделю он решил такое количество задач ᥉ (⌘ frac \ frac). Сколько проблем решил Масса за первую неделю?
Решение: существует дробь ⌘ (⌘ frac \), поэтому знаменатель равен 5. Это означает, что общее число 120 делится на 5, чтобы получить дробь. \(120 \ div 5 = 24 \) имеет одну часть или ߋ(ߋ frac \) числитель равен 2, поэтому нам нужно получить две части, поэтому мы умножаем 24 на 2. \ (24 \ x 2 = 48 \) Ответ задачи: Масса решил 48 задач за одну неделю.
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
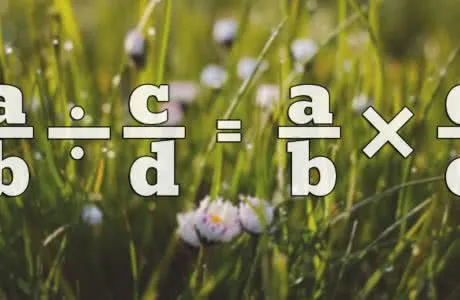
Их можно уменьшить, умножив дробное выражение между ними: *. Эти числа не могут регистрироваться сами по себе, но могут сокращаться по диагонали, выполняя акт распространения: * = =. Распространение только пересекается: первый числитель со вторым знаменателем и наоборот.
Как перевести смешанную дробь в неправильную и наоборот

Смешанные дроби — это запись целых чисел в обыкновенных дробях.
За все пять читается 38.
Для облегчения визуализации можно мысленно добавить знак «+» между целым числом и дробью. Это не ошибка, так как знак плюс опущен для упрощения написания.
Эта нотация подразумевает пять целых пирогов и три восьмых пирога.
Пять квадратов определенного размера и три октавы определенной площади.

Неправильные дроби — это дроби, у которых числитель больше знаменателя. Поэтому из него можно извлечь одно или несколько целых чисел. Потому что каждая неправильная дробь больше единицы.
Возможно и обратное, т.е. преобразование смешанных чисел в неправильные дроби.
Чтобы преобразовать смешанное число в неправильную дробь, умножьте целое число на знаменатель и прибавьте числитель. Полученное значение записывается в числитель. Не изменяйте знаменатель.

Объясните, почему это правильный метод.
Целые числа могут быть записаны в виде дробей, как, например, одна восьмая часть от 40 (40:8 = 5). Помните, что дроби — это деления. Умножьте целое число на знаменатель, чтобы получить число 40. Теперь нам остается только сложить две дроби с одинаковым знаменателем.
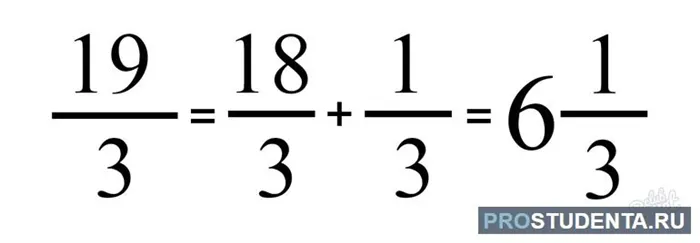
Примеры для перевода смешанных дробей в неправильные

Как уже упоминалось, неправильные дроби всегда больше 1.
Чтобы преобразовать неправильную дробь в смешанную, начните с деления числителя на знаменатель, а затем разделите на целые числа. В числитель записывается целое число, стоящее перед дробью и остатком от деления. Знаменатель остается неизменным.