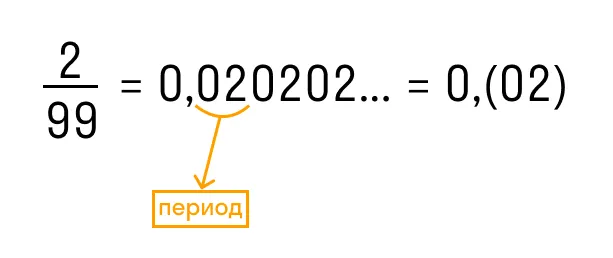
При преобразовании дробей в десятичные дроби другие варианты недоступны. Скажем также, что период (число цифр) бесконечной периодической дроби всегда меньше числа цифр в знаменателе соответствующей обыкновенной дроби.
Дроби
Дроби в средней школе не вызывают особого раздражения. Присутствуют. Пока вам не придется иметь дело с оценками, использующими логарифмы с разумными экспонентами. А вот здесь: …. Вы продолжаете нажимать и нажимать на калькулятор, а он продолжает показывать вам полную таблицу с некоторыми числами. Как третьеклассник, вы должны думать своим умом.
Давайте закончим с дробями! Сколько раз можно путаться в дробях! В конце концов, это просто и разумно: дроби — самая важная часть жизни. Так что же такое фракции?
Виды дробей. Преобразования.
1. обычные фракции, напр.
Иногда вместо горизонтальных линий используются вертикальные: например, 1/2, 3/4, 19/5. Это написание часто используется здесь. Верхние числа называются числителями, а нижние знаменателями. Если имена постоянно путаются (бывает)., «Знаменатель выше твоей головы!». Скажите себе с выражением. Получите зззззззззззззззззззззззззззззззз!»).
Горизонтальные или горизонтальные линии означают, что верхнее число (числитель) делится на нижнее (знаменатель). Вот и все! Вместо тире, знака деления — очень вероятно поставить две точки.
Если есть возможность разделить на целое число, это нужно сделать. Поэтому вместо дроби ’32/8′ гораздо лучше написать число ‘4’. Другими словами, 32 просто делится на 8.
Не говоря уже о фракции «4/1». Это также просто «4». И если оно не делится на дробь, то остается в виде дроби. Возможно, потребуется выполнить обратную операцию. Создать часть целого числа. Но об этом подробнее позже.
2. дробные дроби, напр.
Это форма написания ответа на упражнение «В».
3. смешанные числа, например
Смешанные числа редко используются представителями высших классов. Чтобы работать с ними, нужно превратить их в дроби. Но вы должны быть в состоянии сделать это! Иначе вы столкнетесь с такими числами в задачах и застрянете. Это ничто. Но мы помним процесс! Чуть ниже.
Наиболее универсальной фракцией является нормальная фракция. Мы начнем с этого. Кстати, если дробь содержит логарифм, синус или любой другой символ, это ничего не меняет. Это означает, что любое действие с дробью не отличается от дроби!
Основное свойство дроби.
Ну, тогда поехали! Во-первых, позвольте мне удивить вас. Различные преобразования фрагментов обеспечиваются одним свойством! Его называют основным веществом фракции. Помните: если умножить (разделить) числитель и знаменатель дроби на одно и то же число, то дроби остаются неизменными. Вот этот:.
Понятно, что вы можете продолжать писать до тех пор, пока вам не станет больно. Половины и логарифмы не ставят вас в затруднительное положение. Разберитесь с ними позже. Главное — понять, что все эти различные выражения являются дробями от одного и того же 2/3.
Нужно ли нам конвертировать все это? Да, мы это делаем. Вы узнаете это сами. Используйте основные свойства дробей для сокращения дробей. Это как в начальной школе. Вы делите числитель и знаменатель на одно и то же число, но это все! Невозможно ошибиться! Но люди — творческие существа. Мы можем совершать ошибки где угодно! Особенно если вам нужно сократить дробное выражение, которое содержит все строчные буквы, а не дроби типа 5/10.
В специальном разделе 555 есть способ правильно и быстро сокращать дроби без дополнительной работы.
Обычно студенты не возражают против деления числителя и знаменателя на одно и то же число (или формулу)! Они просто удаляют одно и то же сверху и снизу! Там, где это необходимо, приведены типичные ошибки и промахи.
Например, формула должна быть упрощена.
Вам не нужно ни о чем думать. Удалите букву «А» сверху и букву «А» снизу! Вот и все: правильно.
Правильно. Но на самом деле вы разделили весь числитель и весь знаменатель буквой «А». Если вы привыкли просто удалять, поторопитесь, вы можете удалить ‘a’ в формуле!
Это было бы категорически неправильно. Потому что здесь весь числитель не был разделен на ‘a’! Вы не можете уменьшить эту фракцию. Кстати, такое сокращение будет …. является серьезным вызовом для учителей. Это неприемлемо! Поймите, нужно разделить весь числитель и весь знаменатель!
Сокращение дробей значительно облегчает жизнь. Где-то есть дробь. 375/1000. как вы теперь сотрудничаете? У вас есть калькулятор? Что произойдет, если его умножить, сложить или возвести в квадрат? А если не поленитесь, но аккуратно уменьшите до пяти, еще пять, еще больше. Чем меньше вы его уменьшаете, тем ниже он опускается. Вы получаете три восьмых! Это намного лучше, не так ли?
Фундаментальное свойство дробей заключается в том, что они могут переводить обыкновенные дроби в десятичные и наоборот без калькулятора. Это важно для США, так почему бы и нет?
Для облегчения вычислений вам может понадобиться преобразовать обычные проценты в десятичные дроби и наоборот. Как это сделать, мы объясним в этой статье. В ней рассматриваются правила преобразования дробей в десятичные дроби и наоборот, а также приводятся примеры.
Что такое обыкновенная дробь?
Дробь — это неполное действие деления, а проще говоря, дробь как целое. Долгое время дроби признавались только как части целого. Однако в процессе развития науки пришло время точных расчетов. В то время было понятно, что дроби можно использовать как альтернативу делению, но не совсем.
Когда дроби использовались в качестве альтернативы делению, они просто использовались как число для дальнейших вычислений без потери точности. В зависимости от условий можно использовать обе дроби, и обе они верны.
В обычных пропорциях числитель является делителем, знаменатель делителем, а знак деления указывает на дробную черту. Преобразование дробей в деления не является сложной задачей. Вот пример.
$<5\over<6>> = 5:6 $ — чтобы проверить это утверждение, можно взять калькулятор и использовать это число дважды в одном и том же законе. Хорошо:.
5:6*6 = 5 — Сначала тот же пример, сначала с использованием дробей, а затем действия деления. Результат остается неизменным и не меняется по сравнению с другим примером.
Что такое десятичная дробь?
Десятичные дроби — это числа, записанные делителем. Знаменатель десятичной дроби всегда равен 10.
Чтобы точно найти силу 10 в знаменателе, необходимо измерить десятичную дробь. Например, 0,15 имеет два знака после запятой, поэтому знаменатель этой дроби равен 100.
Первое число 3 без частицы также можно считать десятичной дробью. Только сила 10 в знаменателе равна нулю. Каждое число нулевой мощности дает 1.
Как перевести обыкновенную дробь в десятичную?
Вся значимость метода заключается в том, что десятичные системы используются во всем мире. Благодаря этому используются десятичные дроби. Чтобы преобразовать простую дробь в десятичную, необходимо выполнить действие деления. Это означает, что числитель нужно разделить без знаменателя и уравновесить.
Как вы знаете, не всегда можно разделить одно число на другое. Полученное значение может быть круглым. То есть, повторяется одно и то же число или комбинация чисел. Поэтому не все дроби можно перевести в десятичные числа.
Чтобы правильно преобразовать простую дробь в ее эквивалентное десятичное число, необходимо числитель разделить на знаменатель. По сути, дроби являются делимыми, и между ними нет расхождения.
Свойства десятичных дробей
Ключевым свойством десятичных чисел является то, что добавление одного или нескольких нулей к правой части десятичного числа не изменяет его значения. Это означает, что если в дроби много нулей, их можно просто отбросить. Например:.
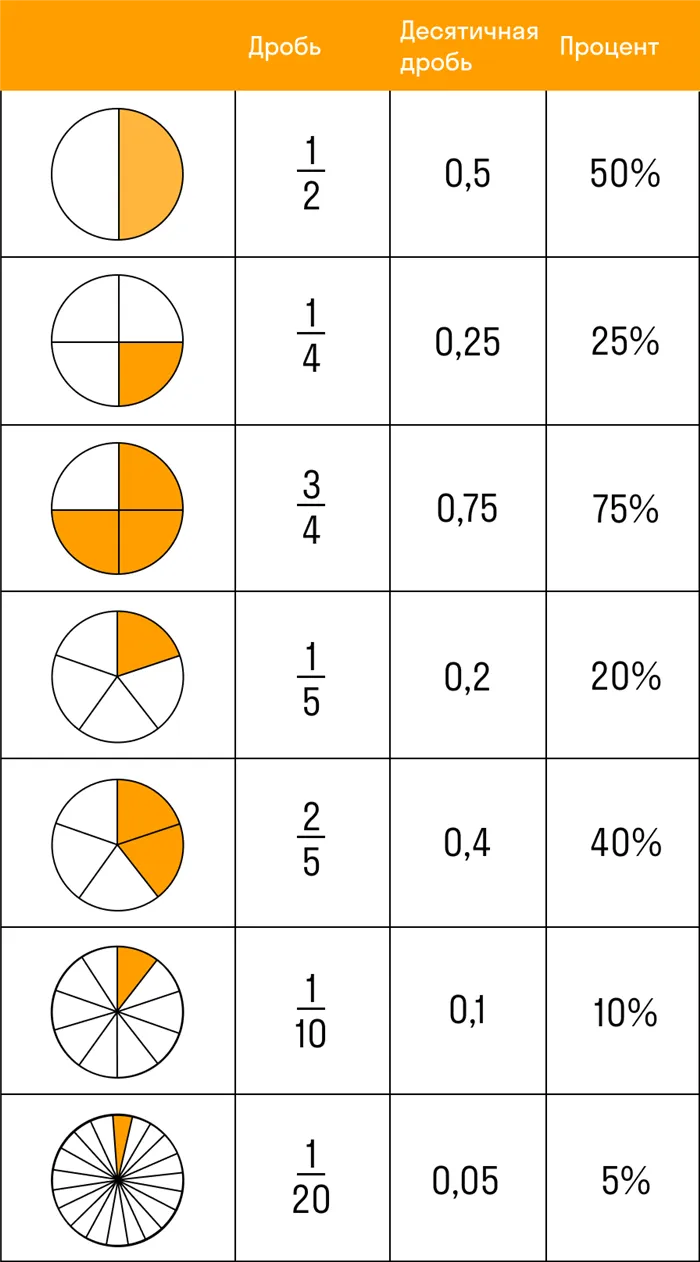
Обычные дроби и десятичные дроби — старые друзья. Вот как их соединить.
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как перевести обычную дробь в десятичную
Прежде чем вы узнаете, как перейти от обыкновенных дробей к десятичным, вспомните разницу между двумя типами дробей и запомните некоторые важные правила.
Десятичные дроби имеют структуру в виде 0,5, 2,16 и -7,42. А вот как это же число выглядит в виде обычной дроби: дробь — это число, которое не является обычной дробью.
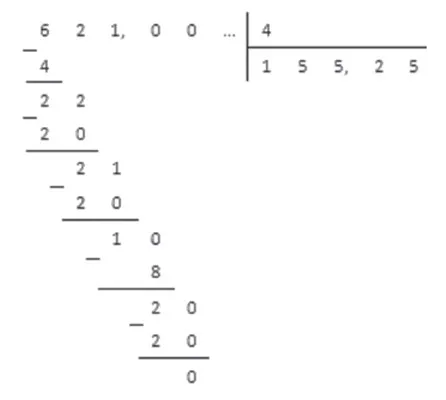
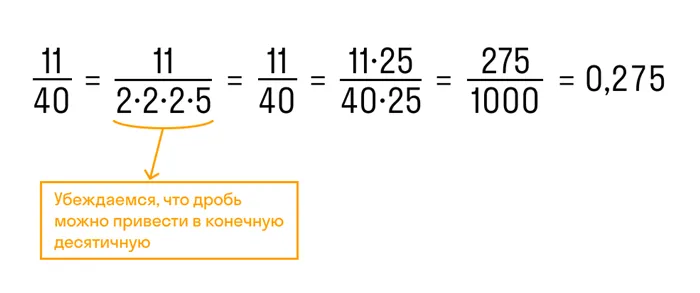
Обычные дроби могут быть преобразованы в конечные десятичные дроби только в том случае, если их знаменатели могут быть разложены на простые множители 2 и 5 любое количество раз. Например.
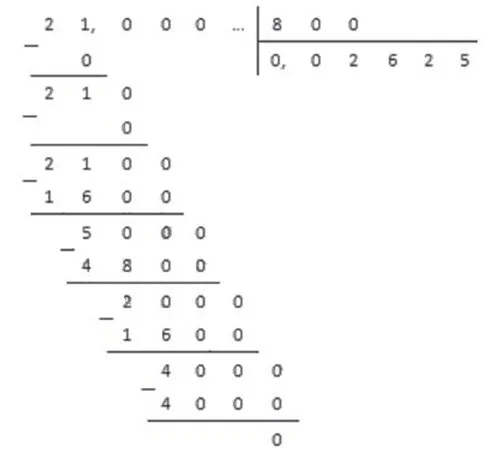
Дробь 11/40 можно преобразовать в конечную десятичную дробь, так как знаменатель можно разбить на кратные 2 и 5.
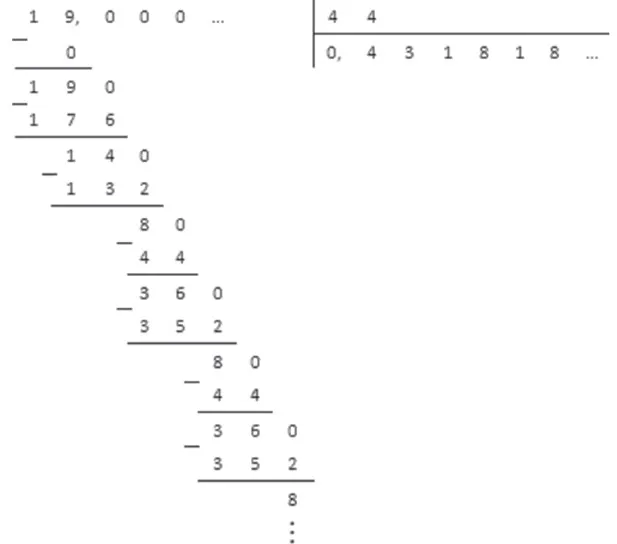
Дробь 17/60 не может быть преобразована в конечную десятичную дробь, потому что ее знаменатель равен 3, а коэффициенты 2 и 5.
Давайте перейдем к самому важному вопросу. Рассмотрите различные алгоритмы преобразования обыкновенных дробей в десятичные.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы преобразовать дробь в десятичную дробь, числитель и знаменатель нужно умножить на одно и то же число, чтобы знаменатель был равен 10, 100, 1000 и т.д. Однако прежде чем приступить к вычислениям, необходимо проверить, можно ли преобразовать эту дробь в десятичную.
В качестве примера возьмем 20/3. Знаменатель дроби делится на множители 2 и 5, поэтому ее можно преобразовать в конечную десятичную дробь.

Вы можете получить 100 внизу и просто умножить 20 на 5. Не забудьте про верхнюю часть; вы получите 15.
Теперь запишите числитель отдельно. Отсчитайте столько же цифр вправо, сколько нулей в знаменателе, и поставьте там запятую. В данном примере знаменатель равен 100 (с двумя нулями), поэтому поставьте запятую после двух цифр и получите 0,15. Преобразование завершено.
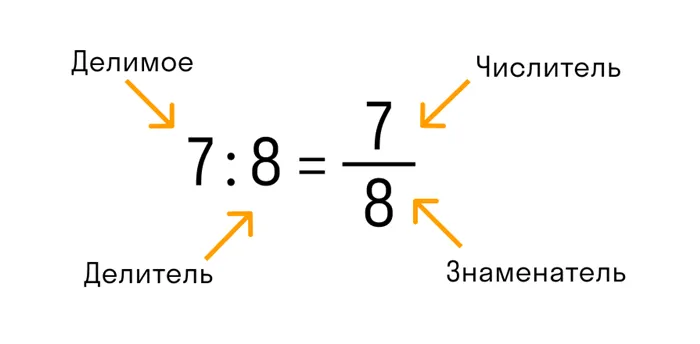
Поскольку оба числа являются простыми, их можно разделить одно на другое или на единицу. Таблицу простых чисел можно без проблем найти в Интернете. Это не имеет прямого отношения к нашему счету, но это не сложно.
Преобразование обыкновенной дроби в десятичную

В этом видеоуроке мы обсудим преобразование десятичных дробей в дробные. Мы увидим, когда несократимые дроби можно перевести в десятичные. В нем также объясняется несколько способов преобразования десятичных дробей в дробные.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим учебным видеокомплектам, необходимо приобрести их в каталоге и добавить в личный кабинет.
Конспект урока «Преобразование обыкновенной дроби в десятичную»
Представьте себе такую историю…
-Как бы вы его развернули? -задается вопросом Саша.
-Что вы не можете решить? спросил Паша.
-На математике от тебя ждут, что ты решишь головоломки к следующему уроку, — ответил он. -А я не умею решать головоломки.
— Не волнуйтесь! -подбадривала она его, Пашу. — Я помогу тебе. Покажи мне головоломку.
— По какой-то причине здесь есть часть клавиатуры для вечеринки, змея с теми же цифрами и буквами, перевернутая коза с вечеринкой, сани с теми же цифрами и буквами, также «E». Саша перечисляет увиденное — я ничего не понимаю, в чем смысл?
— Саша, это простая головоломка, — не согласился Паша. — Сейчас я вам все объясню, и мы вместе разберем слова. Загадка вечеринки означает, что вам нужно убрать из названия картинки столько букв, сколько вечеринок. Если партия находится перед картинкой, уберите букву в начале слова. Если да, — начал объяснять Паша. — Смотрите, первая картинка пазла — это кусочек клавиатуры с акцентированными английскими буквами. Давайте посмотрим, какие буквы соответствуют буквам, выделенным в русской раскладке.
— Это буквы «A», «P» и «R».
— Правильно! — Паша согласился. — Примечание: Первая буква должна быть исключена, так как вечеринка находится перед фотографией. Что же остается?
— Удалив первую букву «А», Саша начал думать. — Остались только буквы «P» и «R».
— Хорошо, я понял! — Паша поддержал своего друга. — Давайте продолжим. Символ равенства рядом с изображением — это символ, заменяющий одну букву другой. Есть даже змея или кобра, а в самом низу есть уравнение, которое заменяет первую букву на картинке на букву «Е». Какое слово стоит после замены?
— Кобра, заменяет первую букву на «Е», получается «еобра», — говорит Саша.
— Правильно! — Паша сказал. — Переходим к следующей фотографии. Если картинка перевернута, значит, слово читается вверх ногами. Более того, я вступил в партию. Поэтому в перевернутом слове первая и последняя буквы должны быть исключены. И что мы получаем?
— Мы вытащили козу, — начал размышлять Саша. -Верхом вниз слово читается: «азок». Затем удалите первую и последнюю буквы. И есть «Зо».
— Превосходно! — Паша был рад за своего друга. — Следующая картинка может решить эту проблему без моего вмешательства?
— Там нарисованы сани, а рядом с ними уравнение, показывающее, что первую букву надо заменить словом «в», — говорит Саша. — Заменив его, вы получите слово «вани».
— Правильно! — Паша согласился. — Теперь мы составляем слово из букв, слогов и слов, которые появляются.
— Теперь, сказал Саша, — есть слово «П», «П», «эобра», слог «ЗО», слово «вани» и буква «е». Подумайте об этом… Это «конверсия»!

— Молодец, Саша!» Друг Паши похвалил.
— Что это за конверсии? — спросил Саша.
— Спроси у Кросавчика, — предложил Паша. — Он обязательно расскажет вам.
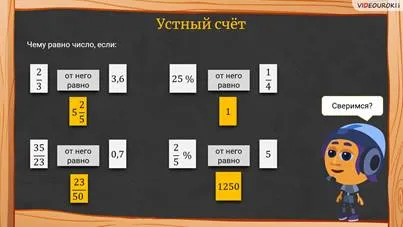
— Дети, прежде чем мы поговорим о преобразовании дробей в десятичные дроби, давайте разомнемся и сделаем несколько устных упражнений, — предложил мудрец.
Однако существуют всевозможные знаменатели. Например, встретиться 3/16. Попробуйте выяснить, как умножить 16 на сколько. Таким образом, вы получите 100 или 1000. Не можете сделать это? Тогда вы можете просто разделить 3 на 16. Если у вас нет калькулятора, вам придется разделить их на квадраты на бумаге, как в средней школе. Вы получите 0,1875.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним очень полезным сервисом можно назвать Калькулятор фрагментов математических ресурсов. Здесь вам не придется ничего рассчитывать самостоятельно. Выберите то, что вам нужно, из предложенного каталога и перейдите к оформлению заказа.
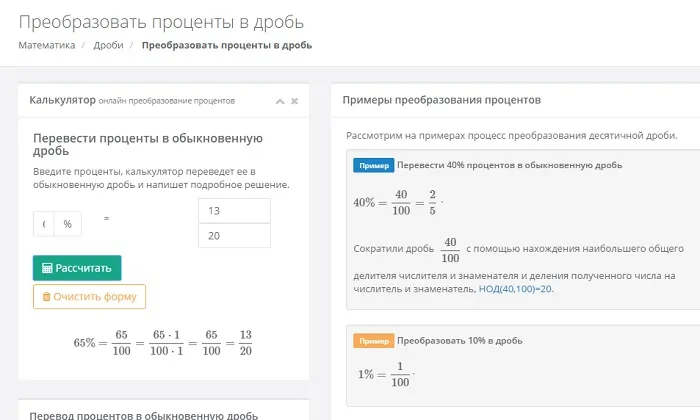
Затем в специально предусмотренном для этого контексте нужно ввести искомое количество процентов и преобразовать их в обычные проценты. Если вам нужны десятичные числа, вы можете легко справиться с задачей перевода самостоятельно или воспользоваться калькулятором, предназначенным для этой цели.
В конце стоит добавить, что неважно, сколько новых услуг не было изобретено или сколько ресурсов не обслуживает вас, голова не болит от того, что вы обучите журнал. Поэтому, безусловно, стоит применить полученные знания и с гордостью помочь своим детям и внукам выучить уроки. Для тех, кто страдает от постоянной нехватки времени, такие онлайн-калькуляторы математических ворот помогут понять, как преобразовать обычные пропорции в десятичные, выполненные вовремя.
Как правило, во взрослой жизни учащиеся не сталкиваются с обыкновенными дробями, а только с десятичными числами. Поэтому с годами знания, полученные в школе, даже очень простые, забываются.
Что такое обыкновенная дробь?
Дробь — это неполное действие деления, а проще говоря, дробь как целое. Долгое время дроби признавались только как части целого. Однако в процессе развития науки пришло время точных расчетов. В то время было понятно, что дроби можно использовать как альтернативу делению, но не совсем.
Когда дроби использовались в качестве альтернативы делению, они просто использовались как число для дальнейших вычислений без потери точности. В зависимости от условий можно использовать обе дроби, и обе они верны.
В обычных пропорциях числитель является делителем, знаменатель делителем, а знак деления указывает на дробную черту. Преобразование дробей в деления не является сложной задачей. Вот пример.
$> = 5:6 $ — чтобы проверить это утверждение, можно взять калькулятор и использовать это число дважды в одном и том же законе. Хорошо:.
5:6*6 = 5 — Сначала тот же пример, сначала с использованием дробей, а затем действия деления. Результат остается неизменным и не меняется по сравнению с другим примером.
Что такое десятичная дробь?
Десятичные дроби — это числа, записанные делителем. Знаменатель десятичной дроби всегда равен 10.
Чтобы точно найти силу 10 в знаменателе, необходимо измерить десятичную дробь. Например, 0,15 имеет два знака после запятой, поэтому знаменатель этой дроби равен 100.
Первое число 3 без частицы также можно считать десятичной дробью. Только сила 10 в знаменателе равна нулю. Каждое число нулевой мощности дает 1.
Как перевести обыкновенную дробь в десятичную?
Вся значимость метода заключается в том, что десятичные системы используются во всем мире. Благодаря этому используются десятичные дроби. Чтобы преобразовать простую дробь в десятичную, необходимо выполнить действие деления. Это означает, что числитель нужно разделить без знаменателя и уравновесить.
Как вы знаете, не всегда можно разделить одно число на другое. Полученное значение может быть круглым. То есть, повторяется одно и то же число или комбинация чисел. Поэтому не все дроби можно перевести в десятичные числа.








