Как правильно вычислить среднее значение. Как находят среднее арифметическое чисел

Говорили о сериях сериалов. Различают конечные и бесконечные ряды. Поговорим о каждом типе отдельно. Поговорили о том, что такое численный полузащитник и как выглядит численный полузащитник. Были приведены примеры использования в реальной жизни.

Как правильно вычислить среднее значение?

Средняя зарплата … Средняя продолжительность жизни… Почти каждый день мы слышим, как эти фразы используются для описания общих цифр. Однако, как ни странно, «среднее» — довольно коварное понятие и часто вводит в заблуждение обычного человека, не знакомого с математической статистикой.

В чем проблема?

Часто то, что понимается под средним, является средним числовым значением, которое сильно варьируется под влиянием отдельных событий или явлений. И у вас никогда не будет точного представления о том, как именно распределяются цены, которые вы изучаете.

Вернемся к классическому примеру средней заработной платы.

В некоторых абстрактных компаниях работают 10 человек. Девять из них получают зарплату около 50 000 рублей, а один зарабатывает 1 500 000 рублей (потому что по странному совпадению он также является управляющим директором этой компании).

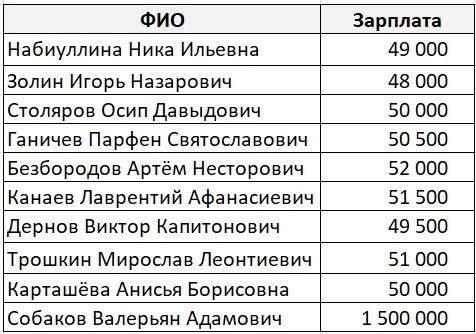
Средняя цена в этом случае составила бы 195 150 рублей, что, по нашему мнению, неправильно.

Какие способы вычисления среднего бывают?

Первый способ заключается в вычислении уже упомянутого арифметического среднего. Это сумма всех значений, деленная на их количество.

• Хорошо работает при нормальном распределении значений в выборке;
• Легко вычислить;
• Интуитивно понятно.

• Не дает реального представления о распределении значений;
• Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Второй способ заключается в вычислении метода, т.е. наиболее распространенного значения

• M₀ – мода;
• x₀ – нижняя граница интервала, который содержит моду;
• n – величина интервала;
• f_m– частота (сколько раз в ряду встречается то или иное значение);
• f_M-1 – частота интервала предшествующего модальному;
• f_M+1 – частота интервала следующего за модальным.

• Прекрасно подходит для получения представления об общественном мнении;
• Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
• Проста для понимания.

• Моды может просто не быть (нет повторов);
• Мод может быть несколько (многомодальное распределение).

Третий способ заключается в разделении упорядоченной выборки на две половины и вычислении через значения между ними. При отсутствии такого значения медианой значений является среднее число между предельными значениями половин выборки.

• M_e – медиана;
• x₀ – нижняя граница интервала, который содержит медиану;
• h – величина интервала;
• f _I – частота (сколько раз в ряду встречается то или иное значение);
• S_M-1 – сумма частот интервалов предшествующих медианному;
• f_m – число значений в медианном интервале (его частота).

рассмотрели основные способы нахождения среднего, называемые мерами центральной тенденции (на самом деле их больше, но эти наиболее популярны).

Теперь вернемся к нашему примеру и рассчитаем все три варианта среднего значения, используя специальную функцию в Expel.

• СРЗНАЧ(число1;число2;…) — функция для определения среднего арифметического;
• МОДА.ОДН(число1;число2;. ) — функция моды (в более старых версиях Excel использовалась МОДА(число1;число2;. ) );
• МЕДИАНА(число1;число2;. ) — функция для поиска медианы.

И вот какие цены мы получили

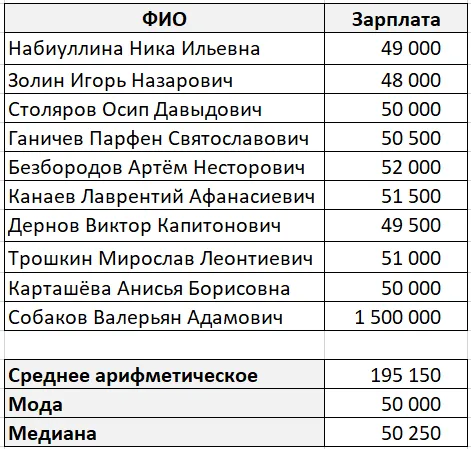
В этом случае метод и медиана гораздо более репрезентативны для средней зарплаты в компании.

Но что произойдет, если, как в примере, выборка содержит не 10 значений, а миллионы? Это невозможно рассчитать в Excel, но не является проблемой в базе данных, где хранятся данные.

Вычисляем среднее арифметическое на SQL

SQL имеет специальную функцию средней концентрации.

Давайте рассмотрим этот процесс подробнее. Все, что нам нужно сделать, это вычислить числовой носитель и получить конечный результат этого числа.

Подсчёт среднего арифметического пары

Самый простой вариант расчета этой величины — вычисление двух чисел. В этом случае процедура выполнения расчета очень проста.

1. Первоначально требуется провести операцию сложения выбранных чисел. Это часто можно сделать, как говорится, вручную, не используя электронную технику.
2. После того как сложение произведено и получен его результат необходимо произвести деление. Данная операция подразумевает разделение суммы двух сложенных чисел на два – количество сложенных чисел. Именно такое действие и позволит получить требуемую величину.

Формула

Таким образом, тип расчета требуемой величины в этих двух случаях следующий

К этому типу применяются следующие символьные выражения

A и B — это значения по умолчанию, для которых необходимо найти цену.

Нахождение значения для трёх

В ситуациях, когда выбираются три значения, расчет этого значения существенно не отличается от предыдущего варианта.

1. Для этого следует выбрать числа, необходимые в расчёте, и сложить их для получения общей суммы.
2. После того как данная сумма трёх будет найдена, требуется опять совершить процедуру деления. При этом полученную сумму надо разделить уже на три, что соответствует количеству выбранных чисел.

Формула

Тип, необходимый для вычисления арифметического 3, выглядит следующим образом

В этом типе используется следующая символика.

a, b и c — это числа, для которых необходимо найти среднее число.

Вычисление среднего арифметического четырёх

Как уже выяснилось по аналогии с предыдущими вариантами, расчет этого значения четырех величин производится в следующем порядке.

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из приведенной выше последовательности для нахождения среднего арифметического из 4, получается следующее уравнение.

В этом уравнении значениями переменных являются.

A, B, C и E — это те, для которых необходимо найти среднее арифметическое.

Применяя эту формулу, всегда можно рассчитать значения, необходимые для определенного количества чисел.

В SQL нет отдельной функции для поиска режима, но вы можете легко и быстро написать ее самостоятельно. Для этого необходимо выяснить, какие зарплаты повторяются чаще всего, и выбрать самые популярные.

Свойства среднего арифметического

1.Среднее арифметическое набора данных из неотрицательных чисел лежит между минимальным и максимальным числом в этом наборе.

2.Среднее арифметическое также следует неравенству среднего значения набора положительных действительных чисел.

a_мин. ≤a_{Средняя гамма} ≤a_Geom ≤a_{Среднее число} ≤a_r.quadr ≤a_Макс. 2 *,.

Другими словами, для набора действительных чисел среднее арифметическое никогда не может быть больше, чем среднее квадратов 1.

Прикладное значение среднего арифметического

Среднее арифметическое значений рассматриваемых данных имеет широкий спектр применения в метрологии и статистике. При обработке результатов измерений их конечное значение часто определяется как среднее арифметическое значений, полученных в результате эксперимента, а стандартное отклонение является оценкой ошибки измерения, поэтому дисперсия и стандартное отклонение являются также включены в результаты расчетов.

Среднее арифметическое семи натуральных чисел равно 12. Восьмое число добавлено так, что среднее арифметическое этих восьми чисел равно 14. найдите восьмое число.

В соответствии со средним арифметическим семи чисел имеем

И для восьми чисел

В таблице есть целые числа, которые больше 40, но меньше 50. Среднее арифметическое всех этих чисел равно -4, среднее арифметическое всех положительных чисел равно 5, а среднее арифметическое всех отрицательных чисел равно -5. (a). Сколько цифр на доске? (b). Какие числа чаще всего пишутся: положительные или отрицательные? c). Какое максимальное количество положительных чисел можно найти между ними?

Пусть всего n будет 40.< n < 50. Пусть k - количество положительных чисел, рассматриваемого множества; m - количество отрицательных, и p - число нулей. Тогда

Согласно определению среднего арифметического, сумма всех чисел равна произведению среднего арифметического и числа.

5-k + -5 —m + 0 —p = -4- n (2.1)

(a). Очевидно, что левая часть уравнения 2.2 делится на 5, поэтому n также должно быть кратно 5. По условию, 40 n n,.

5-k + -5 —m = -180 или m — k = 36, m = 36 + k, (2.3)

m > k, если m ≥ 0 и k ≥ 0. Это означает, что отрицательных чисел больше, чем положительных.

(c). Используйте уравнения 2.1 и 2.3 вместе с n, чтобы найти максимально возможное количество целых положительных чисел, удовлетворяющих задаче. Для p ≥ 0 мы имеем

или заменить первое значение m.

Таким образом, положительных целых чисел может быть не более четырех.

Ответы: a) 45 — b) отрицательный — c) 4.

Υ.Γ. На этой странице используется бета-версия арифметического калькулятора. О недостатках и возможных пожеланиях следует сообщать на форуме сайта (окно для сообщений на форуме находится внизу страницы).

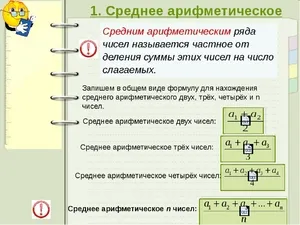
1. другое, возможно, более известное определение: среднее арифметическое чисел — это сумма этих чисел, деленная на количество слагаемых этой суммы (Математика, 5 класс). Среднее арифметическое некоторых чисел равно экспоненте суммы этих чисел, деленной на число слагаемых этой суммы (Алгебра, Макарычев, 7 класс).

2.Когда вычисляется среднее арифметическое данного набора чисел, часто желательно оценить отклонение значений этих чисел от среднего. Оценка отклонения квадрата значений этих чисел от среднего значения является оценкой дисперсии. В целом, термин дисперсия пришел из теории вероятностей. Одно из его основных свойств — изменчивость случайной величины как мера дисперсии случайных величин, связанных с математическими ожиданиями. Не углубляясь в дебри Тер-Вера, здесь представлен только тип дисперсии, используемой при расчете.

-Потом, чтобы получить общую сумму, все эти числа нужно сложить. Конечно, если числа простые и значения небольшие, их можно рассчитать вручную. Однако если все цифры впечатляют, лучше всего использовать калькулятор или электронную таблицу.

Среднее арифметическое

Среднее арифметическое число — это первый параметр в ряду, изучаемом учащимися 5-го класса. Все понятия, связанные с сериями, совершенно неизвестны юным математикам, что может привести к возникновению вопросов и ошибок. Чтобы избежать ошибок в будущем, давайте разберем эту проблему более подробно.

Во-первых, узнайте, что такое поворот. Серия — это количество цифр. Серия может быть конечной или бесконечной. Конечный ряд всегда имеет постоянное количество чисел. Это может быть 2, 3 или 10 миллионов чисел. Все они имеют одинаковый порядок и считаются конечными.

Любое число, произвольно написанное на листе, является конечным рядом чисел.

Возникает логичный вопрос. Если порядок чисел бесконечен, как можно узнать следующий член ряда? В этом нет ничего сложного. Бесконечный ряд всегда имеет формулу для следующего члена и начальное число.

Функции могут быть заменены любым числом и поэтому не считаются числовым рядом. Другими словами, первого члена серии не существует.

Бесконечные ряды изучают в средней школе, а среднее арифметическое в основном ищут для конечных рядов.

Что такое среднее арифметическое?

Среднее арифметическое — это среднее значение ряда. В высшей математике это значение называется трендом, т.е. средним значением ряда.

Чтобы найти среднее арифметическое, необходимо сложить все члены в ряду и разделить сумму на количество членов в ряду. Поэтому, если последовательность бесконечна, то невозможно найти среднее арифметическое всей последовательности, так как невозможно узнать количество членов последовательности. Однако можно найти значение среднего арифметического в отрезках.

Зачем нужно среднее арифметическое?

Среднее арифметическое редко используется в математике, но в реальной жизни оно применяется очень часто. Вот несколько примеров.

• Средним арифметическим в большей части школ вычисляют оценку ученика за четверть. Оценки в этом случае выступают в качестве ряда чисел. Их складывают, а затем делят на количество оценок в общем. Результат округляют, высчитывая оценку за четверть.
• Средняя цена товара. Собирается информация о стоимости товара в каждом магазине. Ценники суммируются и делятся на количество магазинов.
• С помощью среднего арифметического высчитывают урожайность зерна в регионе. Складывают урожайность на каждом поле и делят на количество полей или на количество гектаров.

Это отдельные примеры. На самом деле, среднее арифметическое используется практически во всех областях человеческой жизни. Умение правильно находить среднее арифметическое и понимать, что скрывается за этим термином, необходимо для любой профессии.

Необходимо различать арифметические и геометрические средние. Среднее геометрическое рассчитывается по другой формуле и гораздо чаще встречается в математике. Необходимо понимать, что это две разные функции серии.

Пусть всего n будет 40.< n < 50. Пусть k - количество положительных чисел, рассматриваемого множества; m - количество отрицательных, и p - число нулей. Тогда

Пример решения

Чтобы укрепить теорию, необходимо проанализировать и решить примеры. Например, найдите среднее арифметическое четырех целых чисел 3 2 / 3, 4 5/7 и 63/8.

Решение дается следующим алгоритмом: .

1. Записать величины: 3 2/3, 4 5/7 и 6 3/8.
2. Количество: 3.
3. Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.
4. Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.
5. Вычислить сумму: 2479/168.
6. Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.
7. Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.
8. Значение искомой величины равно 4 463/504.

Если результатом является неправильная дробь, ее необходимо преобразовать в смешанное число. Это считается «правилом этикета» в математике. Это связано с тем, что каждый ответ должен быть преобразован в удобочитаемую аббревиатуру.

Вы также можете использовать онлайн-сервисы для проверки результатов вашей операции. Однако не рекомендуется часто пользоваться этой услугой, так как вы должны быть в состоянии найти ошибки самостоятельно.

Поэтому для вычисления средних арифметических необходимо знать специальные методы, предложенные специалистами в области математики.

Это отдельные примеры. На самом деле, среднее арифметическое используется практически во всех областях человеческой жизни. Умение правильно находить среднее арифметическое и понимать, что скрывается за этим термином, необходимо для любой профессии.

Среднее арифметическое. Среднее значение величины

В этом видеоуроке объясняется среднее арифметическое. Вы узнаете, как вычислять арифметические средние. Вы также узнаете, зачем нужно уметь находить среднее арифметическое.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим учебным видеокомплектам, необходимо приобрести их в каталоге и добавить в личный шкафчик.

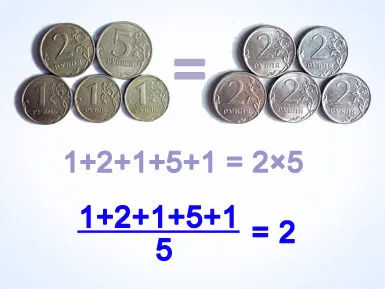
Конспект урока «Среднее арифметическое. Среднее значение величины»

-Паша, здравствуйте. Что вы делаете?

-Здравствуй, Саша. Я прочитал журнал. Я могу себе представить, что каждый человек в России съедает 4,3 кг шоколада в год. Сколько это шоколадных конфет?

-Как вы считаете? Например, я люблю шоколад и могу съесть его очень много, а моя соседка Ваня вообще не ест шоколад. У него на него аллергия. Так откуда у него столько шоколада? Кто-нибудь в России спрашивал вас, сколько шоколада вы едите? Меня никто не спрашивал. Это неправильное число, и неясно, откуда оно взялось.

-Хочешь пойти к Электроше и узнать, откуда у него этот номер?

-У меня новый вопрос. Смотрите, в журнале я прочитал, что каждый россиянин съедает 4,3 кг шоколада в год. И как это считается? Ведь если, например, Ваня не может есть шоколад из-за аллергии, то за год он столько не съест.

-Поясните. Но сначала давайте решим этот вопрос вербально.

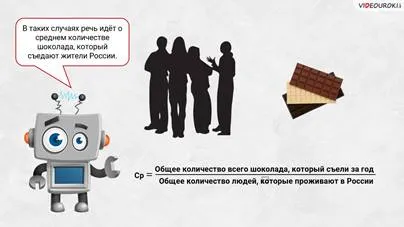
В этих случаях речь идет о среднем количестве шоколада, потребляемого россиянами. Это число рассчитывается путем деления общего количества шоколада, потребляемого за год, на общее число жителей России.

Используя аналогичный метод, вы можете, например, рассчитать средний возраст детей в вашем классе.

Или, например, используя тот же метод, можно найти среднюю скорость набора текста на компьютере.

На национальном уровне используются средние арифметические значения, например, для обозначения 15 тонн пшеницы, собранной с гектара, или среднего размера пенсий.

Для этих целей был придуман специальный термин — среднее арифметическое.

Давайте дадим определение. Среднее арифметическое число — это отношение суммы числа к сумме его компонентов.

Попробуем найти среднее арифметическое чисел:

Если суммы сложить и разделить на три, то среднее арифметическое будет равно 17,5.

-Миссия для тебя, Саша.

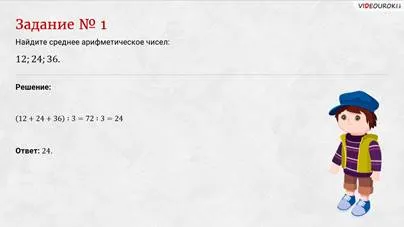
Найдите среднее арифметическое чисел:
Сложим все числа. Так как всего чисел 3, значит, и делить будем на 3. Получим, что среднее арифметическое чисел