Удаление многозначных чисел основано на том, что удаление числа равносильно удалению всех его частей. Из этого свойства видно, что удаление числа равносильно удалению всех единиц, десятков, сотен и т.д. Чтобы утверждать, что 3517 нужно отнять от числа 7228, напишем
Вычитание натуральных чисел: правила, примеры и решения
Ранее мы уже изучали натуральные числа и их свойства для удаления. В этой статье мы представим несколько основных правил, которые помогут вам извлечь натуральные числа. Чтобы информация была легкой для понимания и сразу запоминалась, к теоретическому материалу прилагаются подробные упражнения и типичные примеры.
Добавление и удаление тесно связаны между собой. Удаление противоположно добавлению. Чтобы понять эту информацию, необходимо рассмотреть подробные примеры.
Предположим, что, сложив C и B, мы получим элемент a. Из основных принципов сложения натуральных чисел можно заключить, что C + B = a. Используя дополнительное свойство антагонизма, мы можем преобразовать равенство в b + c = a. Удалив b из b, мы можем заключить, что c. Уравнение a -b = c считается верным. По аналогии, отнимая c от a, b, т.е. a -c = b, получаем его.
Из приведенного выше примера можно сделать вывод, что если сумма c и b равна a, то c — это разность натуральных чисел c и b, а b — это разность a и c. То есть, c + b = a, если c = a -b и b = a -c.
Давайте изменим это утверждение и возьмем важное правило.
Если сумма двух чисел c и b равна a, то разность a — c равна b, а разница равна c.
Теперь мы ясно видим, что добавления и удаления тесно связаны между собой. Из этого факта мы можем сделать вывод о значении.
Снятие — это энергия нахождения суммы, когда известна сумма и другая сумма.
Это определение часто используется в различных примерах и задачах.
Как выполнять вычитание с помощью таблицы
Во многих случаях таблицу сложения можно использовать для нахождения суммы двух чисел, когда известны общее и другое слагаемое.
Рассмотрим это утверждение на примере. Рассмотрим упражнение, в котором нужно найти неизвестную сумму, если известно, что второе слагаемое равно 5, а общая сумма равна 8.
Это можно сделать двумя способами. Используйте графическую визуализацию, где известные числа нарисованы красным и синим цветом.
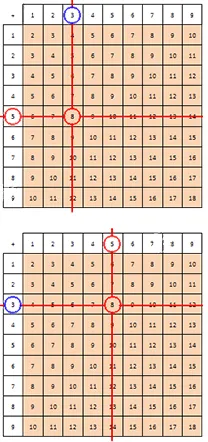
Существует несколько способов сделать это.
Первый метод. Вам нужно найти строку в таблице и известный итог в левой ячейке (вы получите знакомое число 5). Далее необходимо найти столбец, который пересекает линию в ячейке. Эта строка должна содержать известное количество (исходя из примера, число 8). Число, которое вам нужно найти, находится в верхней ячейке найденного столбца. Мы приходим к выводу, что число 3 — это требуемый итог.
Второй метод. В дополнительной таблице необходимо найти столбец, в котором верхняя ячейка содержит известный итог. Найдите линию, которая пересекает знакомый столбец в ячейке, соответствующей известному итогу. Сделайте вывод, что итоговая сумма, которую нужно найти, находится в ячейке слева от этой строки.
Поскольку сложения и удаления, как выяснилось, тесно связаны, эту таблицу можно также использовать для нахождения разностей натуральных чисел. Эту теорию следует подробно рассмотреть на примере.
Предположим, что из 16 нужно удалить 7. Сделайте вывод, что вычитание прослеживается в нахождении числа, которое делает дополнение к числу 7 1 6. Используйте приведенную выше таблицу.
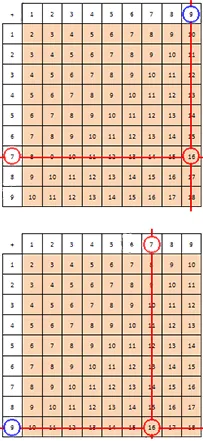
После вычитания 7 из 16 получается искомая разность 9.
Для использования этой таблицы рекомендуется хранить информацию и использовать автоматическую таблицу для создания процесса поиска чисел.
Как производить вычитание разрядов чисел
Сотни тысяч или десятки миллионов могут быть удалены с помощью дополнительных таблиц, рассмотренных выше. По аналогии можно удалить десятки и сотни, чтобы облегчить работу с простыми числами. Например, из 6 сантиметров вычтите 4 сантиметра, то есть 2 сантиметра, что равно 600 — 200 = 400. В других случаях можно использовать таблицы.
Если вы помните, что 100 равно 10 10, вы можете вычислить разницу между десятками, сотнями, тысячами и другими числами, если вы помните, что тысяча равна 1000.
Вам нужно вычислить разницу между 100 и 70.
Переведите числа в десятки. Вы получаете 10 тонн и семь десятков. В дополнительной таблице указано 10 — 7 = 3. Разница между 10 десятками и 7 десятками равна 30, т.е. 100 — 70 = 30.
Необходимо рассчитать разницу между 100 000 и 80 000.
100 000 — это 100 000 и, следовательно, десятки тысяч, 80 000 — это 80 000, т.е. 10 — 8 = 2. 100 000 — 80 000 = 20 000.
Таким образом, удаление и добавление — это взаимные действия. Если известна сумма двух итогов, ее можно преобразовать в разность двух чисел и наоборот. Разница может быть преобразована в сумму.
Способы вычитания
Удалить другой номер можно двумя способами.
В качестве альтернативы, его можно удалить из такого же количества единиц, как и количество единиц, которые содержит меньшая единица. Таким образом, 9 к 6 — это шесть из девяти.
В качестве альтернативы можно добавлять единицы к меньшему количеству, пока не будет достигнуто максимальное количество. Таким образом, вычитая 6 из 9, к 6 прибавляется 3 очка. Разность определяется, когда количество единиц в единице прибавляется к меньшему количеству и приравнивается к большему. Наименьшее число по разности должно быть равно наибольшему числу, поэтому наименьшее число и разность составляют сумму, а наибольшее число — сумму этих двух чисел. Это основа для другого определения абстракции.
Абстрагирование — это акт нахождения другой суммы из заданных суммы и итога.
В этом случае заданная сумма отрицательна, итог удаляется, а подмножеством является другая сумма.
Вычитание многозначных чисел
Удаление многозначных чисел основано на том, что удаление числа равносильно удалению всех его частей. Из этого свойства видно, что удаление числа равносильно удалению всех единиц, десятков, сотен и т.д. Чтобы утверждать, что 3517 нужно отнять от числа 7228, напишем
Удалите единицы отдельно от единиц, десятков и т.д.
Чтобы облегчить удаление, единицы равного порядка вытягиваются влево, в вертикальный ряд, и вставляется знак абстракции, так что разности подписываются внизу, причем меньшие числа подписываются ниже наибольших. Линия.
Ход расчета представлен в устной форме.
Удаление простых единиц: 8 без 7 равно 1. Примечание 1 Под единицами.
Удаление TENS: 2 без 2, подписано 1 под 1 десятком.
Удалите сотни. Пять не может быть отнято от двух и поэтому сразу получает единицу из высших классов (тысяча), обозначенную точкой над семеркой. Один юнит из каждого класса сразу содержит 10 очков в нижних рангах. Добавьте эти 10 единиц к 2 и получите 12 без 12. Когда единица берется из высшего класса, мы ставим точку над классом, из которого она была взята.
Удалите тысячи. Если убрать один, то тысяч будет только 6 вместо 7. Без шестерки получается три, символ под тысячами — 3.
Курс расчета представлен в письменном виде.
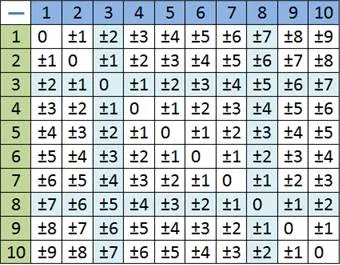
Пример Удалить 6025 из 17004 .
Вы не можете удалить 5 из 4. Добавьте один к десяткам и сразу же добавьте верхние классы, но в этом классе нет единиц. Добавьте до сотен и запишите в точках 7 или больше.
На каждые четыре единицы приходится три единицы из десяти. Отнимите десятки, оставив только 9 9. Добавьте 14 единиц, прибавив 10 к 4.
Удаление:.
Есть один на десятки тысяч. Это происходит потому, что он переносит эту лицемерную цифру на разницу, не изменяя ее.
Ход расчета может быть запечатлен в письменном виде.
Заключительное правило абстракции из предыдущего примера:.
Чтобы выполнить удаление целого числа, добавьте под удаляемое удаляемое так, чтобы единицы равного значения находились в вертикальном ряду, и подпишите разность, проведя под ней черту.
Удаление должно начинаться с простой единицы, т.е. с первого столбца. Затем двигайтесь вправо, затем влево, чтобы удалить сотни тысяч случаев и т.д.
Если абстрактная цифра меньше, чем цифра в аннотации, то разность подписывается в том же столбце — если числа равны, то разность равна нулю. Если цифра реферата больше, чем соответствующая цифра в реферате, прибавьте единицу к следующему разряду реферата, отметьте точкой над цифрой реферата, прибавьте 10 к цифре реферата и удалите. Цифры, обозначенные точками, рассчитываются на единицу меньше.
При удалении цифр занятого разряда, если при сокращении следует ноль, то первый значащий разряд оказывается занятым, над ним ставится точка и все промежуточные нули. Точечные цифры считаются на единицу меньше, а точечные нули — на 9.
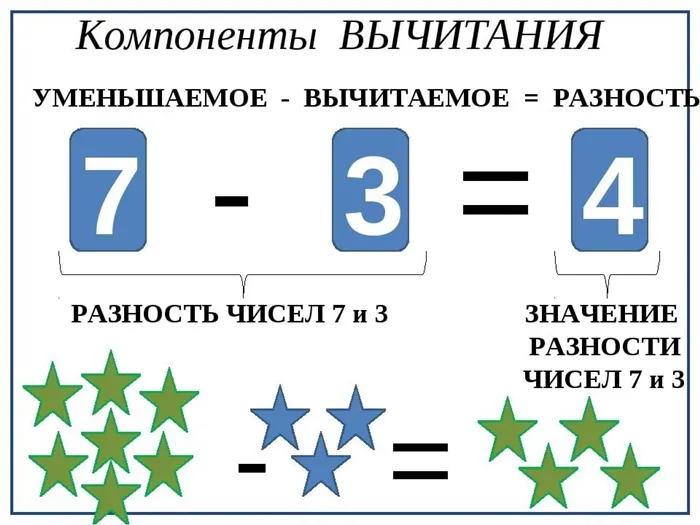
Зависимость между данными и искомыми вычитания
Пример 9 — 6 = 3.
Снятие равно сумме, прибавленной к разности: 9 = 6 + 3.
Удаление равно удалению без разницы: 6 = 9-3.
Разность равна десятичной дроби без удаления: 3 = 9-6.
Численное добавление стоимости. Разность между числом и ближайшей большей единицей называется числовым дополнением. Таким образом, числовые значения 7, 79 и 983 следующие.
10-7 = 3 100-79 = 21 1000-983 = 17
Арифметическое сложение иногда используется для упрощения численных расчетов.
Удаление должно начинаться с простой единицы, т.е. с первого столбца. Затем двигайтесь вправо, затем влево, чтобы удалить сотни тысяч случаев и т.д.
Из приведенных выше свойств видно, что состояние вычета начинается для двух одинаковых целых положительных чисел. Во всех остальных случаях (когда абстракция ≠ удалена) удаление положительных целых чисел не имеет специфического свойства phor. Или, говоря по-другому, лицемерие и абстракция не обмениваются.
Если вычитаемое число больше вычитаемого и вы решили поменять их местами, это означает вычитание большего натурального числа из меньшего натурального числа. В этой системе не рассматривается суть вычитания натуральных чисел.
Для натуральных чисел, где a и b не равны, a-b. B-a. Например, 45-21≠21-45.
Свойство вычитания суммы двух чисел из натурального числа.
Вычитание суммы правых сторон двух натуральных чисел из заданного натурального числа. Это эквивалентно вычитанию первой суммы правых частей из заданных натуральных чисел, а затем вычитанию второй суммы из вычисленной разности.
С помощью букв это можно выразить так:.
где a, b и c — натуральные числа, и должны выполняться условия a> b+c или a=b+c.
Свойство вычитания натурального числа из суммы двух чисел.
Вычитание натурального числа из суммы двух чисел — это то же самое, что вычитание числа из одной суммы, а затем сложение разности и другой суммы. Число, которое можно вычесть, не может быть больше суммы, из которой оно было вычтено.
Пусть a, b и c — натуральные числа. Поэтому, если α больше или равно γ, то выражение (α + β) — γ = (α — γ) + β истинно, а если β больше γ, то (α + β ) — γ = α + (β — γ). Если a и b больше или равны c, то оба последних уравнения справедливы и могут быть записаны в виде
Второй метод. В дополнительной таблице необходимо найти столбец, в котором верхняя ячейка содержит известный итог. Найдите линию, которая пересекает знакомый столбец в ячейке, соответствующей известному итогу. Сделайте вывод, что итоговая сумма, которую нужно найти, находится в ячейке слева от этой строки.
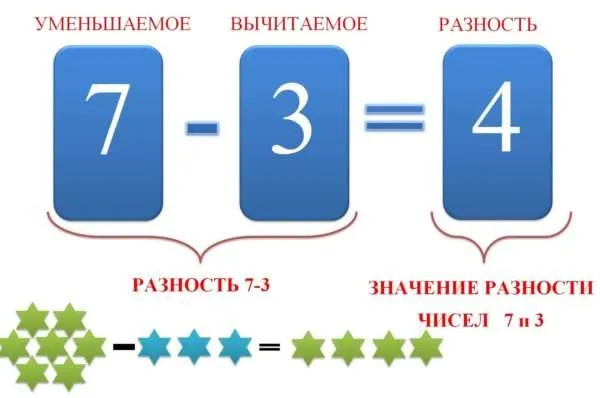
Что такое вычитаемое уменьшаемое и разность: правило
Существует четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они составляют основу математики и используются для выполнения всех других более сложных вычислений. Сложение и вычитание являются самыми простыми из них и взаимоисключающими. Однако термины, которые мы используем для сложения, более распространены в жизни.
Вместе мы говорим о «добавлении усилий» или «количестве достигнутого успеха» при попытке достичь желаемого результата. С другой стороны, названия, связанные с вычитанием, остаются в сфере математики и редко появляются в повседневной речи. Таким образом, термины вычитание, сложение и разность встречаются реже. Правила нахождения каждого из этих терминов могут быть применены только при условии понимания значения термина.
Значение терминов
В отличие от многих научных терминов, заимствованных из греческого, латинского или арабского языков, используемые здесь слова имеют русские корни. Поэтому нетрудно понять, что они означают, и легко запомнить, что они означают.
Терминология.
Что такое разность чисел в математике
Если вы присмотритесь, то увидите, что сами названия относятся к словам «другой» и «иной». Это указывает на то, что между цифрами существуют определенные различия.
Это интересно! Закон действительных чисел и как определить, что они собой представляют.
Этот термин в математике подразумевает, что
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если величины равны друг другу, то между ними нет разницы. В этом случае их разница равна нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшение количества — это сокращение. Затем количество можно уменьшить, удалив его часть. Таким образом, уменьшаемое количество — это количество вычитаемых частей.
Поэтому вычитаемое количество является числом, из которого оно вычитается.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Понимание терминологии облегчает определение правил, по которым располагается каждый вычитающий элемент.
Поскольку разность является результатом определенной арифметики, ее можно найти с помощью этого закона, не прибегая к другим правилам. Однако другие термины математического выражения могут быть неизвестны.
Это интересно! Урок математики: Умножение на ноль — основное правило
Как найти уменьшаемое
Этот термин, как установлено, относится к количеству, на которое удаляется часть. Однако если одна из них удаляется, а другая остается, то число состоит из этих двух частей. Сложив два известных элемента, можно обнаружить неизвестный лицемерный.
Поэтому в данном случае, чтобы найти неизвестное, необходимо добавить абстракции и различия.
| ? | – | 11 | = | 7 |
The unknown is found by adding known items: неизвестное находится путем добавления известных предметов.
| 7 | + | 11 | = | 18 |
Во всех этих случаях верно одно и то же:.
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае, количеств), то удаление одной из них приводит к удалению другой. Поэтому, чтобы найти неизвестные удаления, достаточно отнять разность от целого.
| 18 | – | ? | = | 7 |
В этом примере мы видим, что 18 было удалено из целого числа и осталось 7. Чтобы найти значение, отнимите 7 от 18.
| 18 | – | 7 | = | 11 |
Другие подобные примеры решаются по тому же правилу.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
Таким образом, 45-2 = (40 + 5)-2 = 40 + (5-2) = 40 + 3 = 43. тогда (45-2)-30 = 43-30. выразите подмножество в виде суммы цифровых элементов и завершите вычисления: 43-30 = (40 + 3)-30 = (40-30) + 3 = 10 + 3 = 13
Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило
В этой статье представлены понятия различия, абстракции и редукции.
Арифметика включает в себя всего четыре основных действия, которые называются сложение, умножение, исключение и деление.
Эти действия составляют основу всей математики — и самые простые, и самые сложные могут выполнять вычисления.
Простейшими действиями являются сложение и удаление, которые противоположны друг другу. Факт, что мы используем слово «дополнение» в повседневной жизни.
Например, вы можете столкнуться с фразой «добавить», когда вам придется работать вместе. Но, с другой стороны, «удаление» — это немного сложнее и реже встречается в обсуждениях.
Вы редко слышите такие фразы, как «минус», «удалить» или «разница». В сегодняшней статье мы рассмотрим их с математической точки зрения.
Что значит число уменьшаемое, число вычитаемое и разность чисел?
Абстрактные числа, абстрактные числа, что означает разница? Как мы знаем, многие научные термины и выражения пришли из других языков, часто из греческого и латинского. Однако, поскольку рассмотренные ниже слова имеют русское происхождение, их легче разбить на части.
Например, что можно сказать о разнице между числами? Например, если посмотреть на корень слова «разница», то можно найти омоним «различие».
Если мы говорим о математике, то здесь не о чем задумываться — слово «разница» — это разница между числом, а точнее двумя числами.
Разница говорит нам о том, как одна величина может быть больше другой или, наоборот, как вторая величина может быть меньше первой. В строго математических терминах это выглядит как результат абстракции.
Давайте рассмотрим ближайший пример. Предположим, официантка несет восемь пирожных на диск. Пять из них распространяли их среди покупателей. Сколько коржей остается на диске? Отнимите 5 от 8 и получите 3. Далее, давайте запишем это математически.
Таким образом, разница между 8 и 5 равна 3. Теперь вы понимаете, что означает термин «разница».
Примечание: Если два числа равны друг другу, то между ними нет разницы. Ноль (8-8 = 0).
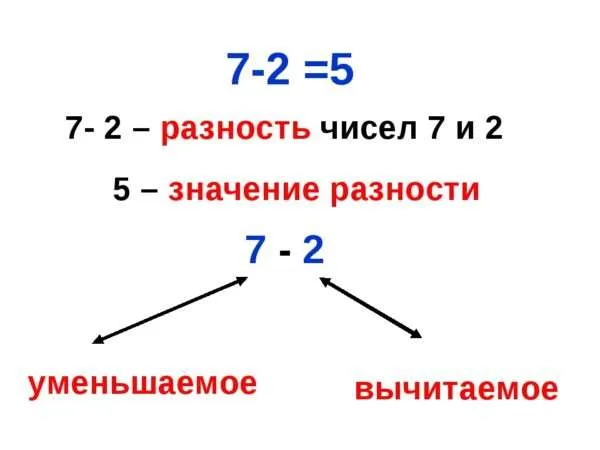
Теперь мы должны выяснить, что такое удаление и уменьшение. Опять же, давайте определим значение термина, исходя из его смысла. Какое число называется абстрактным? Удаление — это число, уменьшенное на величину вычета. С него снимается еще один номер. Что такое абстрактный механизм? Удаляемый номер — это номер, удаляемый из удаляемого номера.
Вернемся к примеру с официанткой. Помните, что он получил пять из восьми и взял три. Мы находим, что три — это разница между двумя числами. Теперь вы можете легко понять, что 8 — это убывающее число, а 5 — абстрактное.
Как найти уменьшаемое и вычитаемое число?
В математике мы уже выяснили, как найти разницу между числами. Это очень легко: просто найдите одинаковое число. Но можно ли найти уменьшаемое и вычитаемое, если числа неизвестны? Конечно, потому что вы знаете два других числа. Например, как найти число сокращений? Если вы знаете значение разности и вычитаемое число, то сумма этих двух чисел равна уменьшаемому числу.
- Y – 10 = 18, где Y – число уменьшаемое
- Значит, Y = 18 + 10
- 18 + 10 = 28
- Y = 28
Что такое разность чисел в математике и как найти разность чисел
В этой статье мы рассмотрим, в чем заключается разница между математическими числами и как человек, интересующийся этой наукой, может найти разницу между числами.
Что такое разность чисел в математике
Удаление — это одна из четырех операций над числами. Он обозначается математическим символом «-» (минус). Удаление противоположно добавлению.
Удаление обычно описывается следующим образом
МАТЕМАТИЧЕСКОЕ ИМЯ.
| A | Уменьшаемое |
| B | Вычитаемое |
| C | Разность чисел |
Число, описывающее разницу, равно 4. Поэтому разность между любыми числами a и b есть такое число c. Это дает сумму a при сложении с b (6 дает 6 при сложении с 4. (6 — 2).
Как найти разность чисел
Само определение показывает, как вычислить разницу между двумя числами. Если чисел меньше, вы можете сделать это наизусть. Детей начальной школы обучают следующему Представьте, что у вас есть пять яблок, и вы берете три из них. Скольким удалось уйти? Правильно — два яблока. Постепенно математика выполняется автоматически, и на вопросы можно отвечать быстро.
Однако эта визуализация не работает с числами больше 50. Поскольку трудно мысленно представить большое количество объектов, то здесь поможет другой способ.
Вычисление разности в столбик
Учащиеся изучают этот метод в рамках курса математики, обычно во втором или третьем классе. Взрослые, пользующиеся калькуляторами, часто забывают, как считать в столбик. Однако калькуляторы не всегда есть в их распоряжении. Это видео освежает школьные знания.
Вычисление разности в столбик – видео
Этот метод также можно использовать, когда нужно удалить большее число, чем меньшее. Это обычно не нужно в реальной жизни, но может быть полезно при решении математических задач.
В примере «a -b = c» предположите, что b больше A. В этом случае c будет отрицательным. Чтобы вычислить разницу, «расширьте» пример: измерьте значение B — A.
Когда разница заканчивается, остается только противоположный знак. Оно будет больше нуля. Чтобы завершить вычисления, добавьте один минус к передней части числа.









