Нежелательно одновременно рисовать два внешних угла на одной вершине. Это усложняет конструкцию и в большинстве случаев не имеет положительного эффекта.
Как найти внешний угол
Или лучше определить дополнительные точки рядом с боковыми сторонами? Это отличный вопрос. Чтобы избежать этой путаницы, в геометрии используется термин «внутренний угол».
Например, в задачах и доказательствах используются внешние углы вершины. Пусть снова вершина $B$ треугольника $\bigtriangleup$. Когда речь идет об углах внутреннего треугольника, можно указать термин «внутренний угол$\угольник$».
Если вы хотите обратиться к внешнему углу, вы можете указать ‘$\angle$outside$angle’.
Режимы «внутренний угол» и «внешний угол» проще и не требуют дополнительных очков. Кроме того, это облегчает определение положения углов треугольника. В конце концов, вы сосредоточены только на вершине.
Это особенно полезно, когда решение проблем или проектирование затруднено. В одной вершине может потребоваться рассмотреть два внешних угла. Они остаются такими же, как и верхний угол, но все же … Маленький. Здесь удобнее дать углам символическое представление в стиле ‘$ \ угол $’ или, например, ‘$ \ угол $’.
Теорема о внешнем угле треугольника
Применим наши знания теоремы к сумме углов треугольников на внешних углах. Рассмотрим внешний угол $\ угол$ большого треугольника на $верхнем треугольнике $\. Сумма внешнего $\угольника$ и внутреннего $\угольника$ равна смежному $180 ^ \circ$.
По теореме о сумме углов для треугольников: $\ угол+\ угол+\ угол=180 ^ окружность \ окружность $
Подстановка переменных из одного уравнения в другое показывает, что внешний угол равен сумме двух других углов, не смежных с ним. Поэтому значение внешнего угла $\ равно сумме внутренних углов $\ + \.
Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних углов, не касающихся треугольника.
Давайте обратим наше внимание еще на одну вещь.
Поскольку внешний угол является суммой двух внутренних углов, внешний угол всегда больше по величине, чем внутренний угол, который его не касается. Это полезный результат, особенно если вам вдруг понадобится доказать возможность или невозможность определенного треугольника или для чего-то другого.
Теорема о внешнем угле треугольника: доказательство Евклида
Формально теорема о внешних углах треугольника была впервые доказана Евклидом, древнегреческим математиком, которого считают «отцом геометрии». Стоит отметить, что его доказательство не имеет никакого отношения к теореме о суммарном угле для треугольников — математики использовали свойства параллельных и квадратичных углов. Это понятно в первую очередь. Евклид потратил много времени на изучение параллельных прямых.
Евклидово доказательство приводится в качестве упражнения и повторения материала по параллельным и квадратичным прямым. На это стоит обратить внимание. Теперь давайте рассмотрим, как внешние углы треугольника «общаются» с параллельными линиями.

Доказательства таковы.
Рассмотрим $\bigtriangleup$ с внешним углом в вершине $B$. Проведите радиус, параллельный ребру $AC$, проходящему через эту вершину. Обратите внимание на полученный радиус $B_1$. Обратите внимание на точку $B_2$ продолжения на стороне $AB$.
Свойства внешнего угла
Это не означает, что существует много свойств внешнего угла. В принципе, если внешние углы включены, то теорема о внешних углах треугольника достаточна для решения задачи или доказательства чего-либо. Теперь и возле внутреннего и внешнего углов.
Другими словами, основное определение.
Однако, когда речь идет о дихотомии, свойства внешних углов обнаруживаются в дополнение к «классическим». Давайте рассмотрим один из самых полезных.
Характеристики сторон внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов перпендикулярны друг другу.
Доказательства таковы.
В треугольнике $ \ bigtriangleup $ постройте внешний $ \ угол $ и внутренний $ \ угол $. Для удобства мы характеризуем все получившиеся углы следующим образом: $ x $ и $ y $ — значения внутренних углов при вершинах $ a $ и $ c $ соответственно. угол- $ f $ — половина внешнего $ \ угла $.
Необходимо определить, чему равно $ z+f $. Если сумма равна $ 90^\ circ $, то свойство доказано. Используйте теорему о внешнем угле и теорему о сумме углов для треугольников.
Нам нужно найти сумму $ z+f $, поэтому мы складываем вышеприведенное уравнение.
3500 (f+z) = 180^\ цир $ после редукции.
Таким образом, сумма $ f $ и $ 1 равна $ 90^^{ circ $. Биссектрисы перпендикулярны друг другу. Собственность доказана.
Характеристики сторон внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов перпендикулярны друг другу.
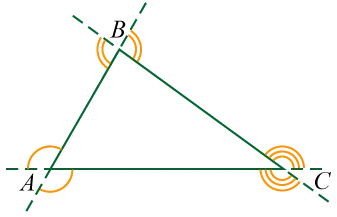
Определение 5. Два угла называются смежными, если они имеют общую сторону и их сумма равна 180° (рис. 1).
Определение 6. Внешний угол многоугольника — это угол, смежный с внутренним углом многоугольника (рис. 2).
Свойства углов треугольника
Общий угол треугольника равен 180°.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
| Углы треугольника |
 |
Общий угол треугольника равен 180°.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
Сумма углов многоугольника равна
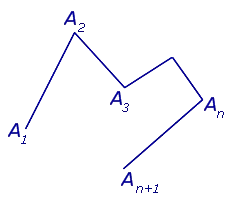
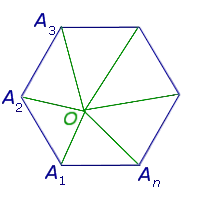
Сумма n внешних углов многоугольника, взятых от одной из вершин, равна 360°.
Сумма углов многоугольника равна
Сумма n внешних углов многоугольника, взятых от одной из вершин, равна 360°.
Это особенно полезно, когда решение проблем или проектирование затруднено. В одной вершине может потребоваться рассмотреть два внешних угла. Они остаются такими же, как и верхний угол, но все же … Маленький. Здесь удобнее дать углам символическое представление в стиле ‘$ \ угол $’ или, например, ‘$ \ угол $’.
Теорема о внешнем угле треугольника: формулировка и задачи
В этой публикации мы рассмотрим одну из основных теорем геометрии 7 класса о внешних углах треугольника. Мы также рассмотрим примеры проблемных вопросов для закрепления представленного материала.
Сначала давайте вспомним, что такое внешние углы. Предположим, у нас есть треугольник:.
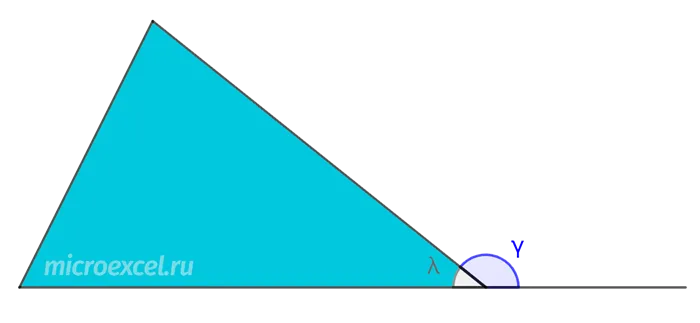
Угол, примыкающий к внутреннему углу (L) того же верхнего треугольника, является внешним углом. На нашей диаграмме он обозначен буквой c.
-
сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не касающихся его.

Из теоремы следует, что внешний угол треугольника больше любого из соседних внутренних углов.
Примеры задач
Задача 1 В треугольнике известны два угла, 45° и 58°. Найдите внешний угол, прилежащий к неизвестному углу треугольника.
Используйте теорему, по которой получено решение: 45° + 58° = 103°.
Внешний угол треугольника задачи 1 равен 115°, а один из несмежных внутренних углов равен 28°. Вычислите значения для остальных сторон треугольника.
Для удобства используйте символику, приведенную для формы выше. Возьмите за основу известный внутренний угол.
Согласно теореме, b = c — a = 115°-28° = 87°.
Угол λ прилегает к внешнему углу и рассчитывается по следующему уравнению (полученному из свойств внешнего угла): λ = 180° — γ = 180°-115° = 65°.
Сумма углов всех этих треугольников равна сумме всех внутренних углов n -угольника плюс сумма всех углов и вершины O. Следовательно, сумма всех углов n -го угла равна
Теорема о величине внешнего угла треугольника по геометрии 7 класса
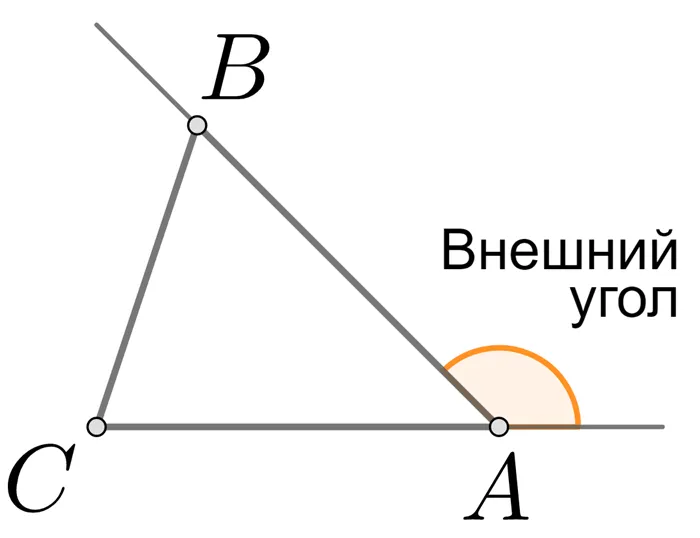
Определение 5. Два угла называются смежными, если они имеют общую сторону и их сумма равна 180° (рис. 1).
Определение 6. Внешний угол многоугольника — это угол, смежный с внутренним углом многоугольника (рис. 2).
Чему равен, как найти при вершине
Чтобы определить местоположение кишки в верхней части, сложите значения не смежных частей уровня, касательных к двум лучам геометрии.
Давайте проиллюстрируем это на примере.
В треугольнике def угол d = 50°, f = 45°. Найдите: vu в каждой вершине фигуры.
Сумма углов в треугольнике всегда равна 180º. \ угол e =180º- Ϯ угол d- Ϯ угол f = 85^Ϯ окружность. GI точек соединения DE и DF равен сумме внутренних углов верхних E и F, т.е. 130º. Соответственно, ГД Е составляет 95°, а ГД F — 135°.
Ответ: ▪Δ = 130°, ∠E = 95° и ρf = 135°.
В треугольнике ABC, b на B с вершиной a = 68° и вершиной c = 55°. ПОИСК: Во внутренних углах В указаны пронумерованные названия углов.
Прилегающие углы складываются, в каждом случае на 180°. Отсюда составляем уравнение: ▪α= 180°-3 =ρ180°-112°= 68°-180°-180°-®2=ρ180°-125°= 55°. Далее отнимите угол с добавлением известного угла: ρα= 180° -α -α -γ = 岐180°-68°-55°= 57°.
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не касающихся его.

Из теоремы следует, что внешний угол треугольника больше любого из соседних внутренних углов.
Внешние углы треугольника были тщательно проанализированы. Мы выделили понятие смежных перпендикулярных углов и указали, какие из внешних углов являются смежными, а какие перпендикулярными. Мы поговорили об известных и неизвестных свойствах внешних углов и обсудили особенности построения внешних углов треугольника.
Внешний угол
Это не только внешние углы треугольника. Такие углы могут быть добавлены к любой форме. Сделайте это и удлините одну из сторон фигуры, а другая сторона образует два смежных угла с этим удлинением.
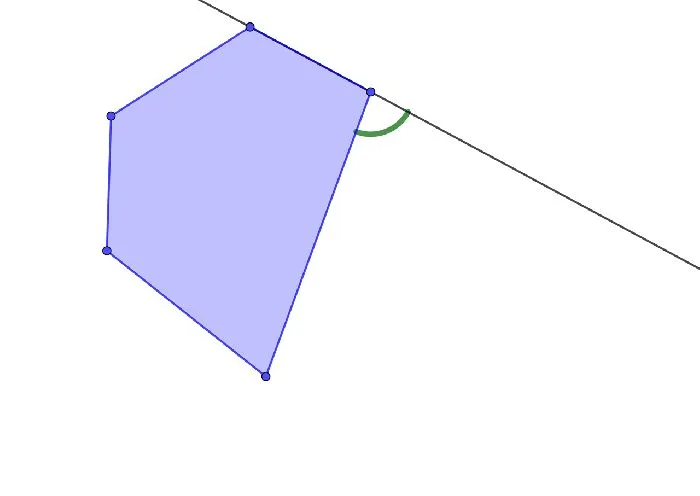
Рисунок 2: Внешние углы пятиугольника.
В каждой вершине фигуры стороны всегда пересекаются. Таким образом, получаются две прямые линии, которые являются продолжением этих сторон, а внешний угол каждой вершины равен 2.
Внешний угол треугольника
Внешние углы треугольника — единственные из всех внешних углов с определенным набором характеристик, которые помогают решить задачу.
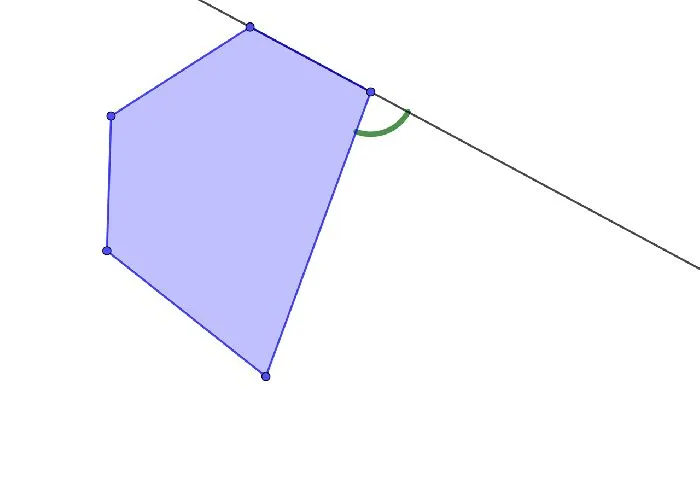
Рисунок 3: Внешние углы треугольника.
Прежде всего, стоит отметить, что редко когда при решении задачи требуется два внешних угла на одну и ту же вершину. Это особенно сложные задачи, часто на уровне олимпиады. Поэтому обычно не стоит заполнять конструкцию и строить два набора смежных углов.
Далее перечислим свойства внешних углов треугольника.
- Внешний угол треугольника равен сумме внутренних углов, не смежных с ним. Это свойство используется чаще прочих и поэтому считается основным свойством внешнего угла. Но есть и другие.
- Сумма трех внешних углов, по одному при каждой из вершин треугольника равняется 360 градусам.
- Если построить два смежных угла при одной вершине, то они будут вертикальны.
Внешние углы треугольника были тщательно проанализированы. Мы выделили понятие смежных перпендикулярных углов и указали, какие из внешних углов являются смежными, а какие перпендикулярными. Мы поговорили об известных и неизвестных свойствах внешних углов и обсудили особенности построения внешних углов треугольника.
Внешний угол треугольника – определение и свойство
Внешние углы треугольника редко используются для решения геометрических задач. Однако каждому ученику желательно знать свойства внешних углов, потому что рано или поздно возникают проблемы в применении этих свойств.

Внешний угол
Внешний угол треугольника — это угол, касательный к внутреннему углу. Треугольник имеет три внутренних угла, сумма которых равна 180°. Смежные углы — это углы, у которых одна сторона лежит на одной прямой, а другая — общая.
Что нужно сделать, чтобы увидеть внешние углы треугольника? Для этого необходимо создать несколько дополнительных структур. Чтобы увидеть внешние углы треугольника, его грани нужно раздвинуть. Каждая вершина имеет два ребра, поэтому вы можете продолжить две прямые линии и два смежных угла.
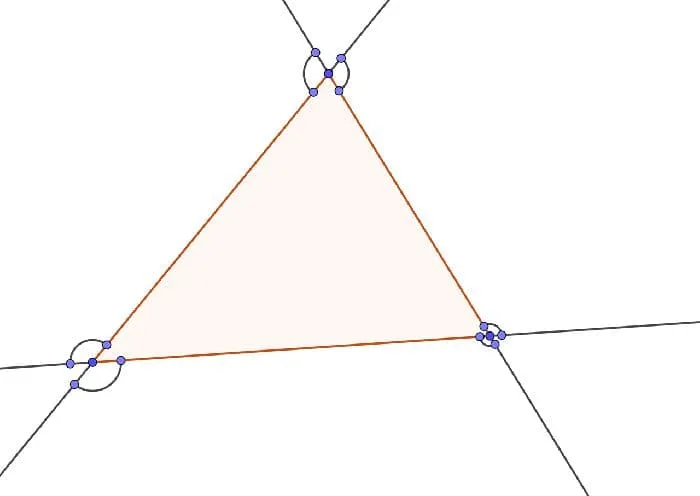
Рисунок 1. Внешние углы треугольника.
Всего существует шесть внешних углов треугольника.
Нежелательно одновременно рисовать два внешних угла на одной вершине. Это усложняет конструкцию и в большинстве случаев не имеет положительного эффекта.
Свойства внешних углов
Существует не так много свойств внешних углов треугольника, и все они связаны с определением внешних углов.
Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов, которые не касаются треугольника. Все очень просто. Сумма смежных углов равна 180. Сумма углов треугольника остается равной 180. Затем мы можем выразить внутренние углы a, b и c и внешний угол d следующим образом.
Вычитание второго уравнения из первого дает
d = c+c — вот доказательство.
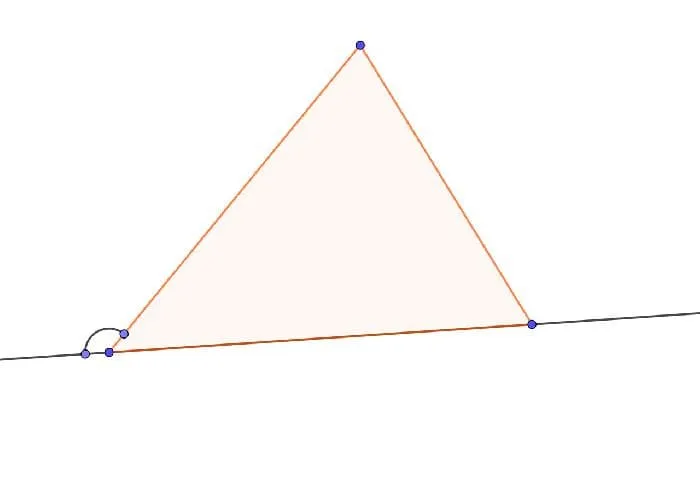
Рисунок 2.Диаграмма для доказательства.
Внешние углы обладают некоторыми дополнительными свойствами.
- Если решение задачи требует одновременного существования двух внешних углов при одной вершине на чертеже, то можно заметить, что эти внешние углы будут равны, как вертикальные.
- Сумма трех внешних углов, по одному при каждой из вершин, равняется 360 градусам.
- Так как внешний и внутренний углы треугольника смежные, то их сумма равняется 180 градусам.
Внешние углы особенно важны при решении тупоугольных треугольников. Важно отметить, что в тупоугольном треугольнике одна из высот всегда внешняя. Эта высота может быть найдена с помощью тригонометрических функций. Для этого необходимо знать внешний угол в случае тупоугольного треугольника и внутренний угол в случае идеального прямоугольного треугольника.
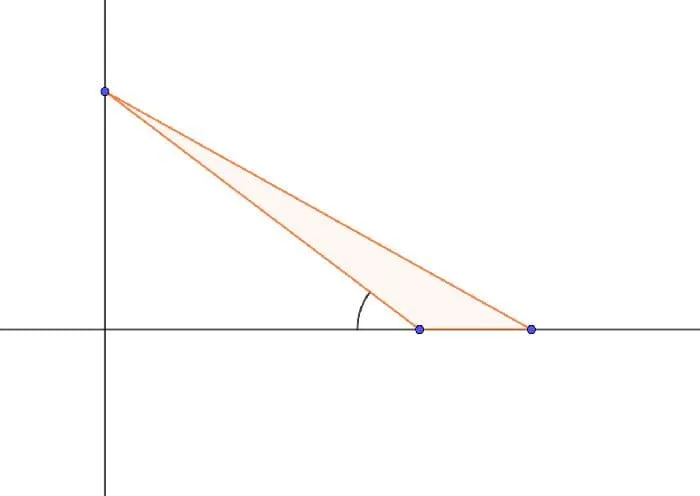
Рисунок 3: Внешние углы тупоугольного треугольника.
Прилегающие углы складываются, в каждом случае на 180°. Отсюда составляем уравнение: ▪α= 180°-3 =ρ180°-112°= 68°-180°-180°-®2=ρ180°-125°= 55°. Далее отнимите угол с добавлением известного угла: ρα= 180° -α -α -γ = 岐180°-68°-55°= 57°.
Сумма внешних углов
Сумма трех внешних углов треугольника, отображенных на разные вершины, равна 360°.
Рассмотрим треугольник ABC.
Каждая пара углов (внутренний и смежный с ним внешний) равна 180° в сумме. Шесть углов (три внутренних и три внешних) вместе равны 540°.
(angle1+∠4)+(angle2+∠5)+(angle3+∠6)=180°+180°+180°=540°
Поэтому, чтобы найти сумму внешних углов, нужно вычесть из общего числа сумму внутренних углов.
∠1+∠2+∠3=540°-(∠4+∠5+∠6)=540°-180°=360°
Изучите видео ролик ниже:
Видео YouTube
Давайте введем еще одно понятие — прямоугольные треугольники. Поскольку мы говорим о различных типах треугольников и их углах, нам необходимо поговорить о прямоугольных треугольниках.
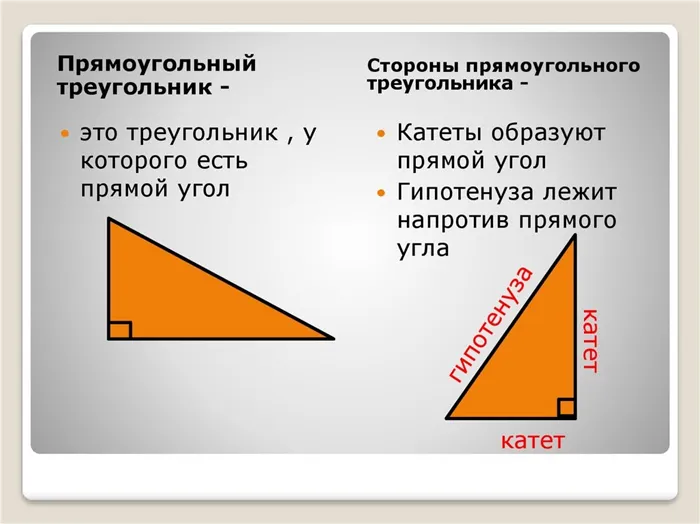
Стоит отметить:. Если углы треугольника равны 180°, а углы прямоугольного треугольника равны 90°, то два других из трех углов равны 180-90=90°. Выводы следующие. Два угла в прямоугольном треугольнике острые, а один — прямой угол.
Практическая часть занятий:
Изучив теоретическую часть, вы, надеюсь, знаете, что сумма углов треугольника равна 180 градусам и что внешний угол треугольника равен сумме двух несмежных с ним углов.
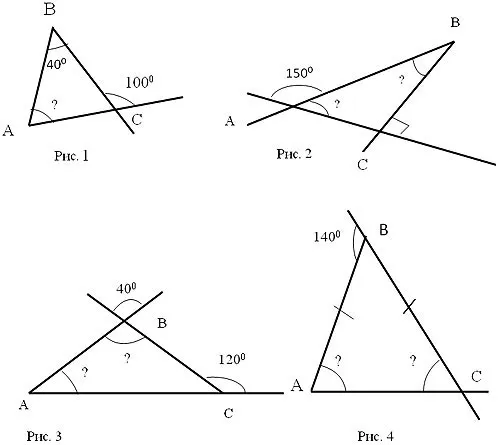
Теперь давайте начнем искать решение.
1. рассмотрим проблему, показанную на рисунке 1. Внешний угол этого треугольника — угол в 100 градусов. равен сумме двух несмежных углов, поэтому неизвестный угол равен 60 градусам.
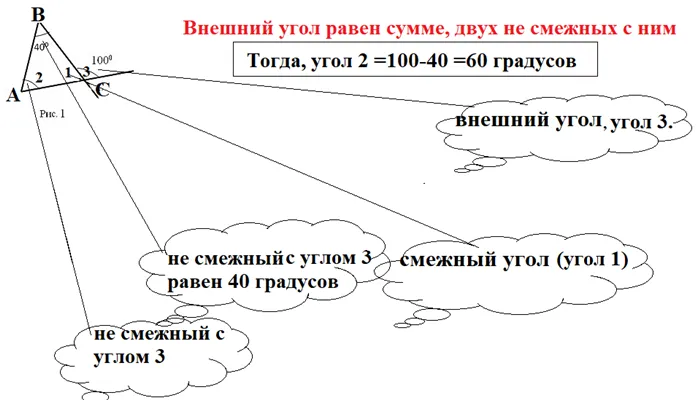
2.Рассмотрим задачу на рисунке 2. На этой диаграмме показаны два внешних угла треугольника; один из них равен 150, а другой — прямой угол = 90 градусов.
Два других дизайна — ваши. (Вам необходимо вспомнить свойства равнобедренных треугольников).








