Математики рекомендуют использовать значения, полученные при расчете конструкции графа, так как произвольные подстановки x и вычисления значительно снижают скорость вычислений.
Как найти вершину параболы неполного квадратного уравнения
Урок: Как построить притчу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Притча — это график функции, описываемой видом AX 2 +BX +C = 0. Чтобы построить притчу, необходимо следовать простому алгоритму.
(1) Один из видов притчи — y = ax 2 +bx +c. Если A> 0, то сектор притчи направлен вверх и 2 +Bx +C = 0.
(a) Полное квадратное уравнение имеет вид ax 2 +bx +c = 0 и решается тождественным b) Неполное квадратное уравнение имеет вид ax 2 +bx = 0. Для решения уберите x из скобки, и каждый множитель будет равен 0: ax 2+bx = 0, x(ax+b) = 0, x = 0, ax+b = 0- c) Форма Ax 2 +C = 0. Для решения перенесите незнакомца в одну сторону, а знакомого — в другую. x = ±√(c/a),.
4) Найдите несколько дополнительных точек для планирования функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
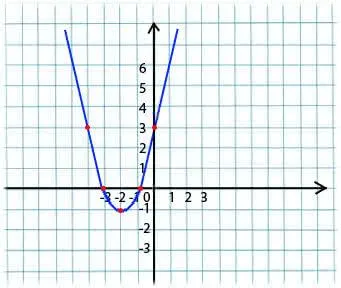
Затем используйте примеры, чтобы проанализировать ситуацию шаг за шагом. Пример №1: y = x 2 +4x +3 c = 3 и притча пересекается при x = 0 y = 3. Ветви притчи смотрят вверх, потому что a = 1 1> 0. a = 1 b = 4 c = 3 x = (-b)2a = (-4)/(2*1) = -2 y = (-2)2 +4*( — 2)+3 = 4- 81 -4ac = 16-12 = 4 x = (-b±√(d))2a x1= (-4+2)2/2 = -1 x2= (-4-2)2 = -3 Возьмем любое место вблизи вершины x = -2
Обменяем y = x 2+4x+3 в уравнении y = (-4)2 +4*(-4)+3 = 16-16+3 = 3 y = (-3)2 +4*(-3)+3 = 9-12+3 = 0 y = (-1)2 +4*(- 1)+3 = 1-4+3 = 0 y = (0)2+4*(0)+3 = 0 -0+3 = 3 Из значений функции метафорой является линия x = -2 мы видим, что она симметрична
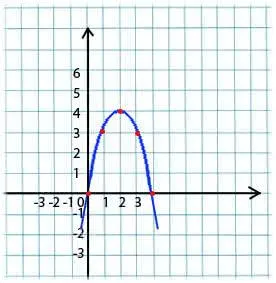
Пример 2: y = -x 2 +4x c = 0 Следовательно, притча пересекается в точке x = 0 y = 0. Ветви притчи выглядят как a = -1 -1 2 +4*2 = -4 +8 = 4 Частное уравнение вида Ax 2 +Bx = 0. Чтобы решить ее, выведите x из скобки и приравняйте каждую силу к 0. x (-x+4) = 0, x = 0, x = 4. Возьмите любую точку около верхней x = 2 x 0 1 3 3 3 3 3 0 y = 0 2 +4*0 = 0 y = — (1)2 +4*1 = -1 +4 = 3 y = — (3)2 +4*3 = -9 +13 = 3 y = — (4) 2 +4*4 = -16 +16 = 0 Уравнение y = -x 2 +4* 4 = -16+16 = 0 Притча симметрична относительно прямой x = 2, что видно из значения функции.
Пример 3 y = x 2 -4 c = 4 Следовательно, притча пересекается в точке x = 0 y = 4. Сектора притчи показаны выше как a = 1 1> 0. a = 1 b = 0 c = -4 x = (-b)/2a = 0/(2*(1)) = 0 y = (0)2 -4 = -4 В верхней части находятся корни уравнения (0; -4 ) x 2 -4 = 0 частное уравнение вида ax 2 +c = 0. Чтобы решить ее, переместите незнакомца на одну сторону, а знакомого — на другую. x = ±√(c/a)x 2 = 4 x1= 2 x2= -2
Возьмем любую точку около верхней x = 0 x -2 -1 1 2 y 0 -3 -3 0 Возьмем любую точку около y = (-2) 2 -4 уравнение y = x 2 -4 = 4-4 = 0 y = (-1) 2 -4 = 1-4 = -3 y = 1 2 -4 = 1-4 = -3 y = 2 2 -4 = 4-4 = 0 Убедитесь, что притча симметрична прямой x = 0 от значения функции Обратите внимание, что функция y = ax 2 + bx = -3
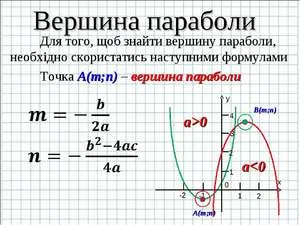
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c. Где a — первый коэффициент, b — второй коэффициент, а c — свободный термин, называемый притчей. Обратите внимание, однако, на тот факт, что a ≠ 0.
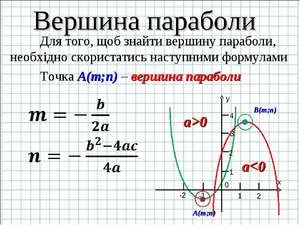
Каждая точка в притче имеет симметричную ей точку, кроме одной, которая называется верхней точкой. Чтобы найти верхнюю точку, необходимо установить точку на графике. Точка графика — это определенная координата оси абсцисс и вертикальной координатной оси. (x; y). Узнайте, как найти свои любимые номера.
Первый способ
Если вы хотите узнать, как правильно вычислить координаты пиков, проверьте вид x0 = -b/2a. Замените это число в функции, чтобы получить y0.
Найдите первый и второй коэффициенты и свободные члены.
Замените значения a и b в формуле и
Это означает, что верхняя часть находится в точке (4; -1).
Ветви притчи симметричны относительно оси симметрии, проходящей через верхнюю часть притчи. Зная корни уравнения, легко вычислить удаленную верхнюю позицию притчи. Предположим, что k и n — корни квадратного уравнения. Тогда точка x0 равна k и n и может быть вычислена по виду x0 = (k + n)/2.
Например, рассмотрим y = x 2 -6x+5
2) Найдите различие, используя вид: d = b 2 -4 ac:.
3) Используйте вид (-b ± √d)/2a для нахождения корней уравнения.
Второй способ
Прибавление к полному квадрату — лучший способ определить, где находится вершина. Используя этот метод, можно одновременно вычислить x и y, не заменяя исходный пример на x. Рассмотрим этот метод на примере функции: y = x 2 +8 x +10.
1. сначала выражение должно быть приравнено к переменной, равной 0. Затем, чтобы переместить c вправо с противоположным знаком, мы имеем выражение x 2 + 8x = -10. 2.
2. нам нужно создать идеальный квадрат с левой стороны. Для этого измерьте (b/2)2 и увеличьте обе части уравнения до полученного результата. В этом случае замените b на 8.
Вы получите 16. Затем добавьте это число к обеим частям уравнения.
3. мы видим, что полученное уравнение является совершенным квадратом. Его можно выразить в виде: (x + 4)2 = 6.
Используйте это уравнение, чтобы найти координаты вершины притчи. Чтобы вычислить x, мы приравниваем 0 к 0. Таким образом, x = 4. Координата y равна координате справа, y = 6. Вершина притчи в этом уравнении — (-4, 6).
Третий способ
Если вы знаете, что такое деривативы, для вас есть другой человек. Независимо от того, где находится «угол» притчи, ее вершина — это крайняя точка. В этом методе необходимо применить следующий алгоритм
1. найдите первую производную, используя вид f ‘(x) = (ax² + bx + c)’ = 2ax + b.
2. выровнять производные по 0. В итоге получается 0 = 2ax + b. Отсюда вы можете найти то, что нас интересует.
Для получения дополнительной информации ознакомьтесь с этим методом.

Построение параболы
Самой сложной частью построения является нахождение правильной точки функции. Для детальной структуры необходимо рассчитать 5-7 пунктов (достаточно для школьного урока). Для этого выберите значение x и замените его функцией. Результатом вычисления является количество точек на оси линии. Затем нанесите точки на координатный уровень. В результате вы получаете притчу.
Давайте рассмотрим подробнее, как найти точки интереса. Например, функция y = -x 2 +11 x -24 имеет вид (5,5; -6,25).
Из-за осевой симметрии притчи можно измерить только значения справа или слева от вершины. Это удобнее, так как желательно измерять цену, наиболее близкую к 0. В нашем случае эти значения равны 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Если функция представлена в виде неполного квадрата, то к обеим частям уравнения нужно прибавить или вычесть одно и то же число. Используя этот метод, можно одновременно рассчитать значения x и y. Алгоритм нахождения вершины функции y=x 2 + 4x+2 следующий.
Нахождение вершины параболы: способы, примеры, советы
График функции y=ax 2 + bx + c. Где a — первый коэффициент, b — второй коэффициент и c — свободный член, называется параболой. Заметим, однако, что a ≠ 0.
Каждая точка в притче имеет симметричную ей точку, кроме одной, которая называется верхней точкой. Чтобы найти верхнюю точку, необходимо установить точку на графике. Точка графика — это определенная координата оси абсцисс и вертикальной координатной оси. (x; y). Узнайте, как найти свои любимые номера.
Первый способ
Если вы хотите узнать, как правильно вычислить координаты пиков, проверьте вид x0 = -b/2a. Замените это число в функции, чтобы получить y0.
Найдите первый и второй коэффициенты и свободные члены.
Замените значения a и b в формуле и
Это означает, что верхняя часть находится в точке (4; -1).
Ветви параболы симметричны относительно оси симметрии, проходящей через вершину параболы. Когда корни уравнения известны, можно легко вычислить дальнее положение вершины параболы. Предположим, что k и n — корни квадратного уравнения. Тогда точка x0 равна k и n и может быть вычислена по уравнению x0 = (k + n)/2.
Например, рассмотрим y = x 2 -6x+5
2) Найдите различие, используя вид: d = b 2 -4 ac:.
3) Используйте вид (-b ± √d)/2a для нахождения корней уравнения.

Второй способ
Прибавление к полному квадрату — лучший способ определить, где находится вершина. Используя этот метод, можно одновременно вычислить x и y, не заменяя исходный пример на x. Рассмотрим этот метод на примере функции: y = x 2 +8 x +10.
1. сначала выражение должно быть приравнено к переменной, равной 0. Затем, чтобы переместить c вправо с противоположным знаком, мы имеем выражение x 2 + 8x = -10. 2.
2. нам нужно создать идеальный квадрат с левой стороны. Для этого измерьте (b/2)2 и увеличьте обе части уравнения до полученного результата. В этом случае замените b на 8.
Вы получите 16. Затем добавьте это число к обеим частям уравнения.
3. мы видим, что полученное уравнение является совершенным квадратом. Его можно выразить в виде: (x + 4)2 = 6.
Используйте это уравнение, чтобы найти координаты вершины притчи. Чтобы вычислить x, мы приравниваем 0 к 0. Таким образом, x = 4. Координата y равна координате справа, y = 6. Вершина притчи в этом уравнении — (-4, 6).
Третий способ
Если вы знаете, что такое деривативы, для вас есть другой человек. Независимо от того, где находится «угол» притчи, ее вершина — это крайняя точка. В этом методе необходимо применить следующий алгоритм
1. найдите первую производную формулы f'(x) = (ax²+ bx + c)’ = 2ax+b
2. выровнять производные по 0. В итоге получается 0 = 2ax + b. Отсюда вы можете найти то, что нас интересует.
Для получения дополнительной информации ознакомьтесь с этим методом.

Построение параболы
Самой сложной частью построения является нахождение правильной точки функции. Для детальной структуры необходимо рассчитать 5-7 пунктов (достаточно для школьного урока). Для этого выберите значение x и замените его функцией. Результатом вычисления является количество точек на оси линии. Затем нанесите точки на координатный уровень. В результате вы получаете притчу.
Давайте рассмотрим подробнее, как найти точки интереса. Например, функция y = -x 2 +11 x -24 имеет вид (5,5; -6,25).
Из-за осевой симметрии притчи можно измерить только значения справа или слева от вершины. Это удобнее, так как желательно измерять цену, наиболее близкую к 0. В нашем случае эти значения равны 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Найдите правильную цену.
Перечислите промежуточные расчеты на бумаге. Это не только облегчит поиск вершины, но и поможет вам заметить свои ошибки.
Делайте все постепенно. Следуйте алгоритму.
Пожалуйста, обратите внимание:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Функция — это (уникальное!) множество функций, где каждому элементу множества (аргументу) ставится в соответствие (уникальный!) элемент другого множества (множество значений функции). Правило заключается в том, что элемент присваивается элементу.
Квадратичная функция
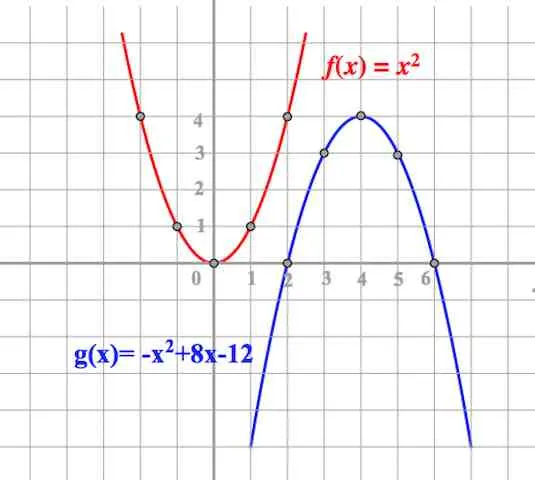
Чтобы построить его, заполните таблицу, заменив значение x в выражении.
Отметьте точки (0; 0), (1; 1), (-1; 1) и т.д. Чем меньше уровень координат (чем меньше значение, в данном случае шаг 1) и чем больше значений x вы получите, тем более гладкой будет кривая), получите притчу.
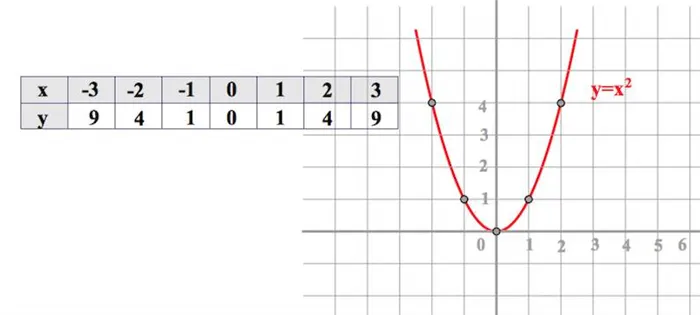
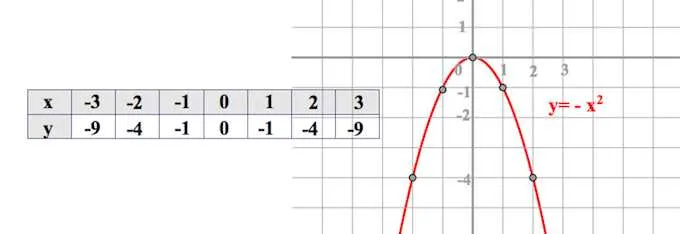
Взяв случай, т.е. даже при наличии симметрии (x), легко убедиться, что симметрия существует. Это легко проверить, заполнив соответствующие таблицы.
II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ
Что происходит, когда мы берем? Как меняется поведение в притче? Притча меняет форму и «теряет вес» по отношению к притче (не верите мне — заполните соответствующую таблицу и убедитесь сами):.
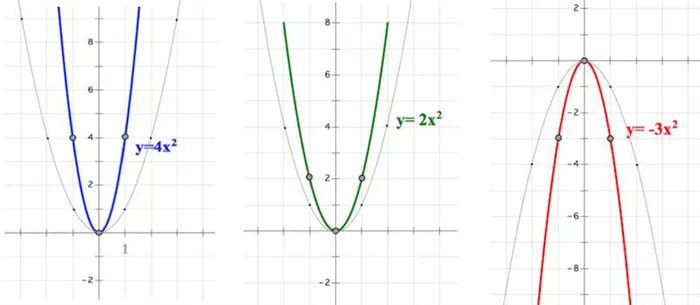
На первом рисунке (см. выше) хорошо видно, что точки (-1; 1) из таблицы притчи (1; 1) преобразуются в точки (1; 4) и (1; -4). Одинаковое значение, придаваемое каждому пункту, умножалось на 4. Это происходит для всех значимых точек в исходной таблице. Аналогично, рассмотрим фотографии 2 и 3.
Притча была бы «шире», чем даже если бы.
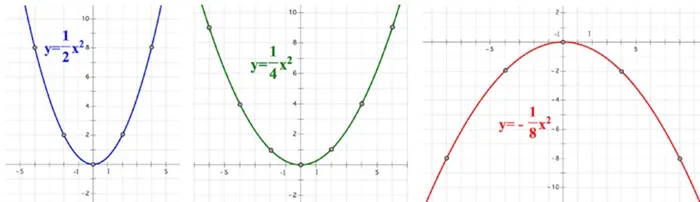
1) Сигнальные знаки отвечают за направление ветки. Если ветви направлены вверх, если вниз.
(2) Абсолютное значение коэффициента (модуля) показывает, будет ли притча «расширяться» или «сужаться». Чем он больше, тем длиннее притча, чем меньше | a |, тем шире притча.
III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»
Вот игра, с которой вас можно познакомить (т.е. где посмотреть дело), рассмотрим притчу о форме. Нетрудно сделать вывод, что притча движется вверх и вниз вдоль оси (вы всегда можете обратиться к таблице).
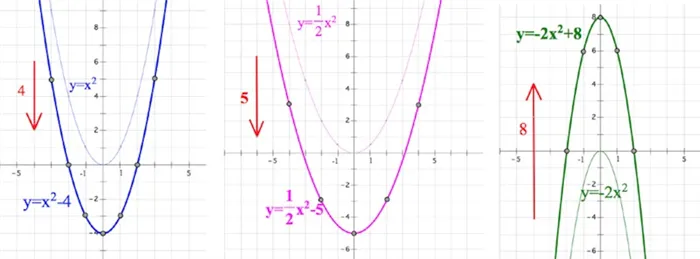
IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»
Когда притча «сбегает» с оси и в итоге «проходит» по всему уровню координат? Когда она перестает быть равной.
Здесь нам необходим тип расчета вершины для построения притчи.
Таким образом, в этой точке (как в новой системе координат (0; 0)) мы строим притчу, которая уже находится в нашей власти. Если мы имеем дело, например, с отрезком сверху вправо и один к одному — полученная точка является нашей точкой (так же как шаг влево и шаг вверх является нашей точкой) — если мы имеем дело, например, с отрезком сверху вправо и два вверх Например.
Нахождение экстремальных точек является важным шагом в решении многих практических задач. Конечно, можно открыть специальный электронный калькулятор, но предпочтительнее уметь делать это самостоятельно.
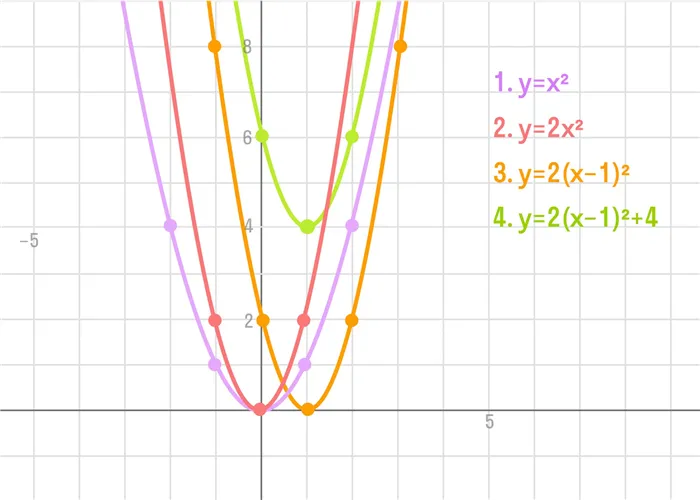
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Уравнение квадратичной функции можно записать в виде y = a(x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x).0) + y0где x0, y0 — Это координаты вершины притчи.
Координаты вершины — (x₀;y₀). В уравнении квадратичной функции y = 2x 2 + 3x -5 второй коэффициент является иго, если a = 1.
Рассмотрим такой пример: y = 2 * (x -1)2 + 4.
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
Составьте график притчи для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x-2) x (x + 1).
Этот тип функции позволяет быстро найти нулевую точку функции.
(x-2) x (x + 1) = 0, т.е. x₁ = 2 и x₂ = -1.
Определите координаты вершин параболы.
Найдите точку пересечения осей OY.
c = ab = (-2) x (1) = -2, что симметрично относительно оси симметрии параболы.
Отметьте эти точки на координатной плоскости и соедините их прямыми линиями.








