В результате пересечения двух биссектрис внутреннего и внешнего углов получается угол 900. Внешний угол треугольника — это угол, касательный к внутреннему углу треугольника.
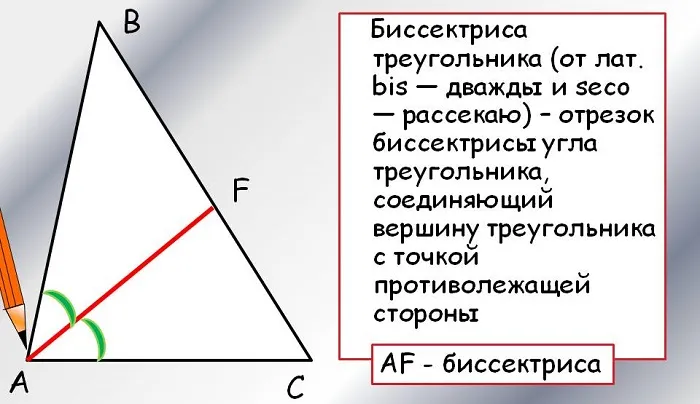
Биссектриса
Биссектрисы угла (от лат. bi- «двойной» и sectio «рассекаю») — это радиусы при вершине угла, которые делят угол на два равных угла1. Биссектриса угла — это геометрическое место точки угла, равное стороне угла.
В треугольнике биссектриса угла может также означать часть этого угла до его пересечения с противоположной стороной треугольника.
Содержание
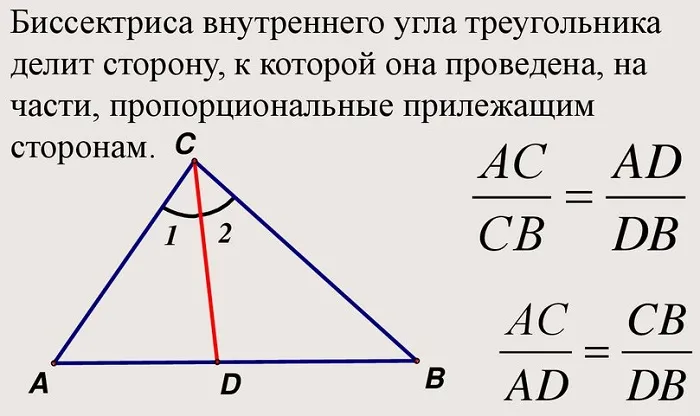
- Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
- Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
- Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
- Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
- Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
- Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, 2 причём даже при наличии трисектора. 3
- ↑ Биссектриса // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Учебные трудности пятиклассников
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Биссектриса» в других словарях:
Bisector-S, g. Bisectris f. Математика. Прямая линия проходит через вершину угла и делит его на центры. BAS 2. Дихотомический дизайн. Васюкова 1999. биссектриса — вид грызуна, проходящего через рога и разделяющего рога посередине. 1994.Белянин. Рекс. Brokg …. … Исторический словарь французского языка.
Биссектриса — Математика, линии, русские синонимы прямые линии. Bisectrisa Существительное, количество синонимов: 3-Line (182) — … Словарь синонимов.
(От лат. bis — дважды, от secon — измельчать) Угловой угол — это полуокружность (радиус), идущая от вершины угла и делящая его на две …
Biscectrix — ISE, bisectrix, fem. (от лат. biscectrix — разрезать сбоку) (мат.). 1. в углу — прямая линия, разделяющая средний угол. 2. в треугольнике — прямая линия, проведенная из угла к противоположной стороне, делящая стороны по местам.
bissektrisa -bissektrisa, s, fem. В математике: радиус (3x.) Он исходит из вершины угла и делится на середину. Словарь Ожегова. С. Ожегов, Н. Шведова. 1949 1992 … Словарь Ожегова.
Биссектриса, С., Г. Школьный преподаватель математики. Из шк… Словарь Аргона о России.
Биссектриса — А. С. Гольдберг. англо — энергетический словарь России. 2006 г. Энергетика выпускает общую среднюю линию … Словарь технических переводчиков
дихотомос — радиус, который начинается от вершины угла и делит его на две части — каждая часть биссектрисы одинаково удалена от стороны угла. Три угла треугольника b. Треугольники пересекаются в точке, находящейся в центре треугольника … Большая политехническая энциклопедия.
Bisectrix- (Biscetectrice (biscectricis) лат. радиус, проходящий наполовину через верхнюю часть угла. Новый словарь иностранных языков. Edwart, 2009. bisectricisis, bisectrix, g. Из лат. Biscectrix -… … … Словарь иностранных языков.
Biscectrix -s; гр. франц. bisectricis от лат. bisectricis дважды, надежно разрезать мат. Радиус, выходящий из вершины угла и разделяющий его на две части. *Биссектриса угла (дважды от латинского bis, со второй дискеты), начиная от вершины угла и разделяя на две … Полуконсольная линия (радиус), разделяющая на энциклопедические словари.
Можно использовать алгебраические инструменты. Свойства соотношений, нахождение неизвестных величин и решение алгебраических уравнений при решении геометрических задач.
Определение и свойства биссектрисы угла треугольника
В публикации рассматривается определение и основные свойства деления треугольных углов, а также приводятся примеры решения задач для закрепления изложенного материала.
Угловой отрезок — это радиус, который начинается от вершины угла и делит этот угол с центром.
Биссектриса треугольника — это часть, которая соединяет вершины углов противоположных треугольников и делит этот угол на две равные части. Эта биссектриса также называется внутренней биссектрисой.
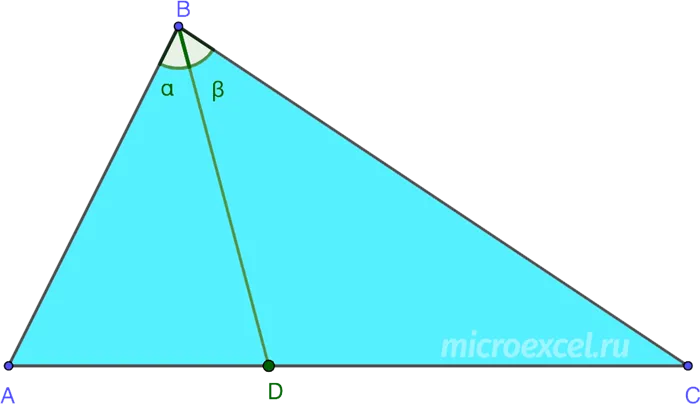
Основание биссектрисы — это точка на стороне треугольника, в которой начинается биссектриса. Другими словами, в нашем случае это точка D.
Биссектриса угла, прилежащего к внутреннему углу треугольника, называется внешней биссектрисой.
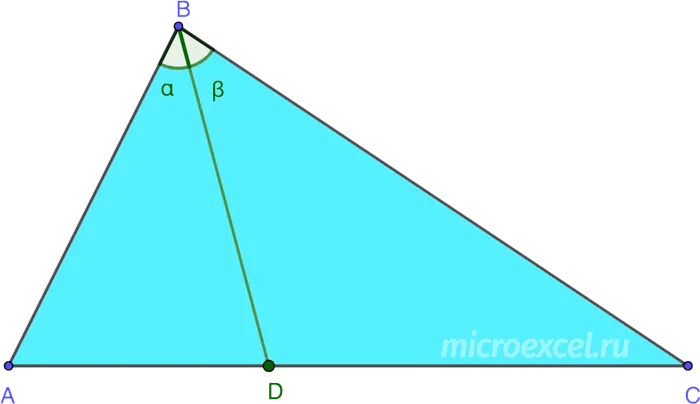
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону на части, равные отношению сторон, прилежащих к этому углу. Итак, в случае нашего треугольника (см. диаграмму выше):.
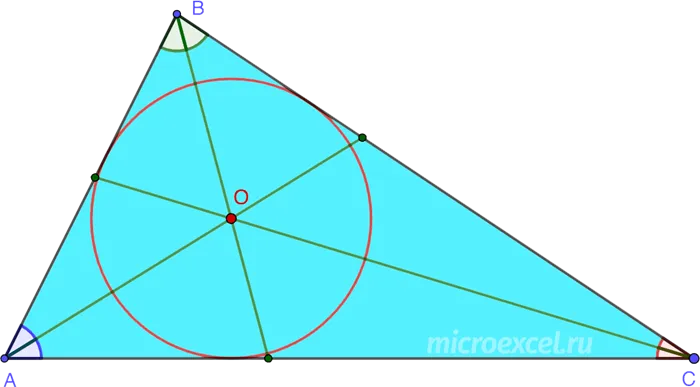
Свойство 2
Пересечение трех внутренних делений треугольника (называемых центрами) является центром окружности, записанной на диаграмме.
Свойство 3
Все треугольники, участвующие в пересечении, делятся на подобия, где сумма последовательных сторон углов делится на противоположную сторону (измеряется сверху).
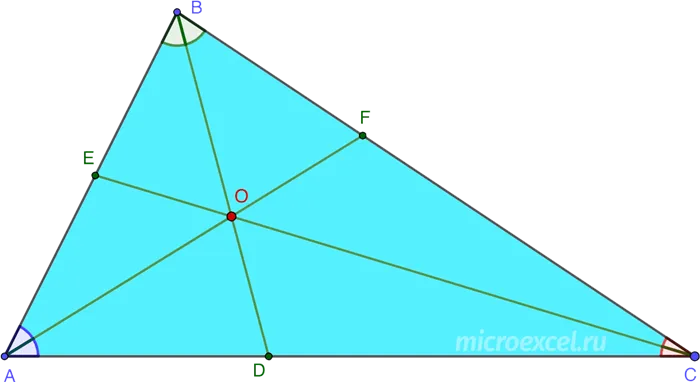
Свойство 4
Если известна длина отрезка, образованного на стороне, пересекающей дихотомос, на двух других сторонах треугольника, то длина отрезка находится по формуле (полученной из теоремы Стюарта)
BD 2 =ab⋅BC -ad любовь

Свойство 5
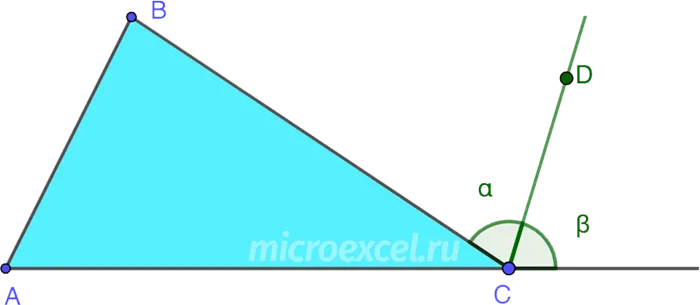
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг другу.
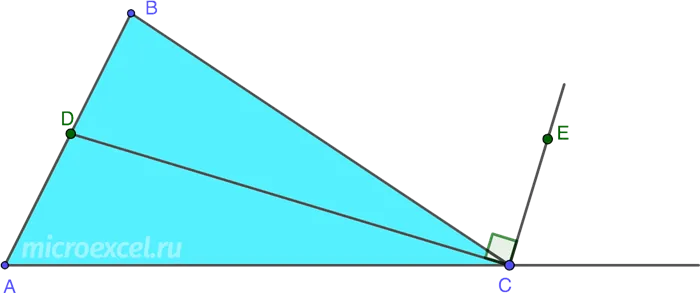
- CD – внутренняя биссектриса ∠ ACB ;
- CE – биссектриса угла, смежного с ∠ ACB;
- ∠ DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с размерами 6 см и 8 см. Найдите длину дихотома, вписанного в нижнюю часть.
Решение заключается в разработке плана в соответствии с условиями задачи.
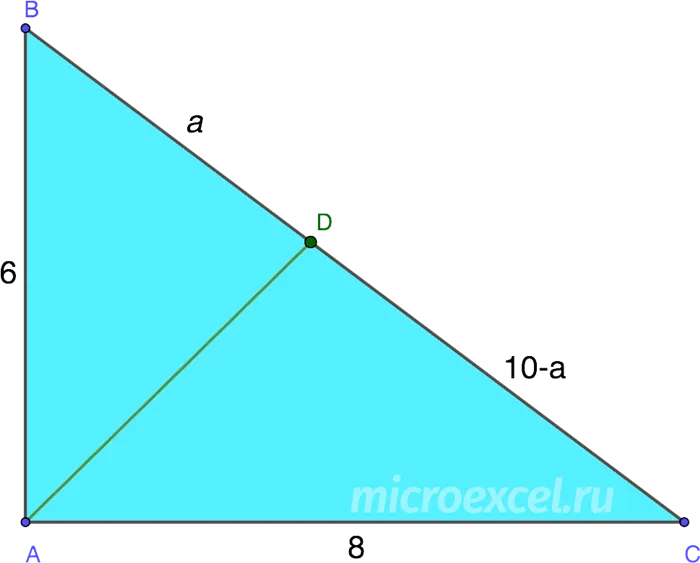
Длину подчиненного элемента можно найти, применив теорему Пифагора (его квадрат равен сумме квадратов двух вершин). BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100. bc = 10 см.
Затем создайте отношение согласно утверждению 1 в подчиненном условном разделе BD как «A» (Тогда dc = «10-a»).
![]()
Уберите дроби и решите полученное уравнение: 8a = 60-6a 14 = 60a ≈ 4,29
Поэтому Bd ≈ 4,29 см, а Cd ≈ 10-4,29 ≈ 5,71 см.
Теперь длину биссектрисы можно вычислить по типу, приведенному для свойства 4.
Обратное также имеет место. Если через вершину провести прямую линию, параллельную основанию изотреугольника, то верхняя внешняя биссектриса является частью этой линии.
Вычисление биссектрисы треугольника с известными свойствами

Как известно, математика — царица наук. Неслучайно это выражение так любимо учителями, особенно в старших классах. Математика открыта только для тех, кто умеет рационально мыслить, и, во-вторых, для тех, кто всегда хочет получать ответы, причем решения, основанные на анализе, а не на обмане, опять же построенном на рациональных связях. Эти качества, рожденные со школьной скамьи, могут сформировать серьезную жизнь взрослых людей, как на рабочем месте, так и в другие трудные времена.
- Свойства
- Свойства в равнобедренных треугольниках
- Определение биссектрисы треугольника
- Определение длины
- Нахождение величины угла
Сегодня многие люди сталкиваются с проблемами при решении математических задач, возникшими в начальной школе.
Однако даже ученики, успешно освоившие программу математики начальной школы и перешедшие на новый этап школьной и жизненной жизни, где алгебра отделена от геометрии, могут столкнуться с серьезными трудностями. Однако, как только ученик научится и, главное, поймет, как найти разбиение треугольника, он всегда помнит о средствах массовой информации. Рассмотрим треугольник ABC с тремя перегородками. Как видно из диаграммы, все они сходятся в одной точке.
Первая — биссектриса треугольника, которая является одной из самых важных характеристик, и мы видим, что этот отрезок делит угол посередине. Таким образом, в приведенном выше примере плохой угол равен углу DAC.
Это интересно: как найти периметр треугольника.
Свойства
- Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
- Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.
Свойства в равнобедренных треугольниках

- Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
- Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
- Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
- Все биссектрисы равностороннего треугольника обладают равенством.
Определение биссектрисы треугольника
В треугольнике ABC предположим, что стороны AB = 5 см и AC = 4 см. Сечение CD = 3 см.
Определение длины
Длина может определяться следующими типами. AD = квадратный корень из произведения разности сторон и соответствующей части.

Найдите длину стороны BC.
- Из свойств известно, что BD/CD = AB/AC.
- Значит, BD/CD = 5/4 = 1,25.
- BD/3 = 5/4.
- Значит, BD = 3,75.
- ABxAC = 54=20.
- CDxBD = 33,75 = 11,25.
Таким образом, чтобы вычислить длину, отнимите 11,25 от 20 и получите квадратный корень из результата 8,75. Результат, включая миллиметры, составляет 2,958.
Цель этого примера — явно создать ситуацию, когда длина промежутка, как и все другие величины в математике, не выражается в физических числах, но я не боюсь.
Это интересно: какова эволюционная природа социального развития?
Нахождение величины угла
Чтобы найти углы, образованные отрезком, важно сначала вспомнить сумму углов, которая всегда составляет 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA равен 50 градусам. Поэтому простой расчет выглядит так: CAB = 180 (70+50) = 60 градусов.
Используя основное свойство, если угол, из которого он получен, разделить на два, то каждый из них имеет равный угол и CAD, который равен 60/2 = 30 градусов.
Если нужны дополнительные примеры, рассмотрим ситуацию, когда вы знаете только плохой угол в 28 градусов и угол ABC в 70 градусов. Используя свойства здания, умножьте значение плохого угла на 2, чтобы быстро найти угол кабины. CAB = 282 = 56. Поэтому BAC = 180 (70+56) или 180 (70+282) = 180 126 = 54 градуса.
Мы специально рассмотрели случаи, когда этот участок выступает в качестве медианы или высоты, оставляя другие специальные статьи.
Таким образом, были рассмотрены такие понятия, как биссектриса треугольника, изучены их виды, найдены их длины и углы и применены к приведенным примерам, наглядно показывая, как их можно использовать для решения других задач по геометрии. С этим также связаны такие понятия, как медиана и высота. Проведите ночь в компании красивых проституток в Санкт-Петербурге. Посетив наш онлайн-портал, вы сможете выбрать самых подходящих девушек в вашем городе. Изучение всех возможных вариантов поможет вам выбрать правильного партнера! Если этот вопрос выяснен, то следует перейти к дальнейшему изучению других свойств треугольников. Это не означает, что дальнейшее изучение геометрии немыслимо.
Обратное также имеет место. Если через вершину провести прямую линию, параллельную основанию изотреугольника, то верхняя внешняя биссектриса является частью этой линии.
Определения понятия биссектрисы
Биссектриса треугольника — это часть треугольника, которая делит его углы на два равных угла. Например, если треугольник имеет угол 120 0, то при проектировании окклюзии образуются два угла по 60 0.
Кроме того, поскольку треугольник имеет три угла, можно спроектировать три бисектора. Все они имеют точку пересечения. Эта точка является центром окружности, зарегистрированной в треугольнике. В противном случае эта точка пересечения называется центром треугольника.
В результате пересечения двух биссектрис внутреннего и внешнего углов получается угол 900. Внешний угол треугольника — это угол, касательный к внутреннему углу треугольника.
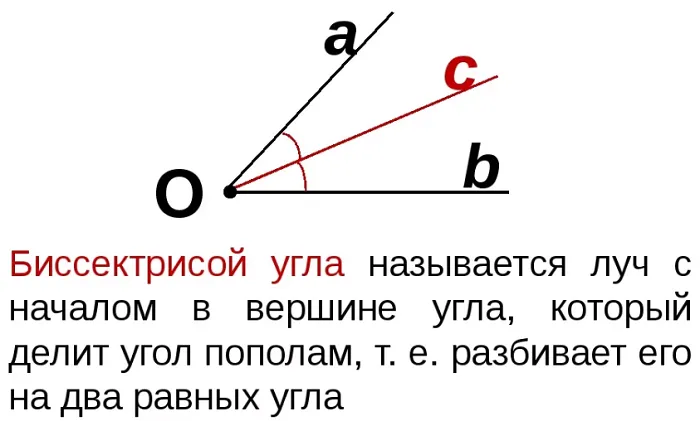
Рисунок 1. Треугольник с тремя биссектрисами
Биссектриса делит противоположную сторону на два отрезка, связанных сторонами.
Точка пересечения равна стороне угла. То есть на одинаковом расстоянии от сторон угла. Другими словами, если конструкция спроектирована перпендикулярно к каждой стороне угла треугольника из любой точки деления, то эти перпендикуляры будут равны …
Если медиана, биссектрисы и возвышение спроектированы одной вершиной, то медиана является самой большой частью, а возвышение — самой маленькой.
Некоторые свойства биссектрисы
В некоторых типах треугольников биссектрисы обладают особыми свойствами. Это относится в основном к треугольникам изошеллы. Эта форма имеет два одинаковых аспекта, третий из которых называется основанием.
Построение биссектрисы из вершины угла треугольника изошеллы к основанию обладает свойствами высоты и высоты. Аналогично, длина биссектрис совпадает с длиной высоты и возвышения.
- Высота – перпендикуляр, опущенный из вершины треугольника к противоположной стороне..
- Медиана – отрезок, который соединяет вершину треугольника и середину противоположной стороны.
Это также относится к равносторонним треугольникам, т.е. треугольникам, у которых все три стороны равны.
Пример задания
В треугольнике ABC, BR — биссектриса, AB = 6 см, BC = 4 см и RC = 2 см. Отнимите длину третьей стороны.
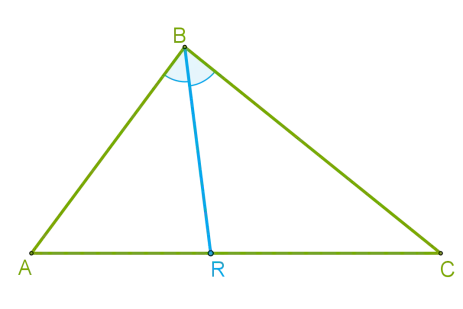
Рис. 3. Биссектрисы треугольника
Биссектриса делит сторону треугольника на определенные соотношения. Используйте это соотношение для выражения AR. Затем найдите длину третьей стороны как сумму отрезков, на которые эта сторона делится биссектрисой.
Затем используйте всю секцию AC = RC+ AR
В треугольниках изошелла биссектрисы, вырезанные в основании, делят треугольник на два равных прямоугольных треугольника.
8. треугольники изошеллы могут быть использованы для определения взаимного расположения высот через биссектрисы, спроектированные из одного и того же места. В частности, медиана и высота расположены по разные стороны третьего ряда.
Примеры решения задач
Задача №1
При dabc love = 90° биссектрисы острых углов построены. Участок, соединяющий пересечение центральной головки и ее основания, перпендикулярен катетеру. Найдите угол для этой конкретной фигуры.
Пусть am am = 90°, AD — биссектриса, медиана, o — точка пересечения медиан, od⊥bc.
Тогда oe: ob = 1:2 в соответствии с междисциплинарным свойством.
Поскольку od⊥bc, odiioc, следовательно, dbod к dbec согласно аналогичному второму свойству, поэтому db = 1:2 согласно аналогичным состояниям формы.
Это означает, что CA:AB = 1:2.
Поскольку катетер находится на половине предмета, ∠ABC = 30°, следовательно, CAB = 60°.
Задача №2
Диагональ прямоугольника делит его острый угол на центры. Докажите, что этот прямоугольник является ромбом.
Поскольку ABCD — прямоугольник, DAC= ∠ACB как пересечение лагерей AD, BC и вторичного AC.
По договору ∠DAC=∠ACB=∠BAC, поэтому DACB — равнобедренный, т.е. AB = BC, поэтому ABCD — ромб.








