Как найти углы четырехугольника. Как найти углы четырехугольника

Площадь ромба также можно найти, умножив его стороны на высоту, приходящуюся на эту сторону. Однако не путайте высоту с прилегающей стороной. Высота — это линия, которая выходит из любой вершины ромба на противоположную сторону и пересекает противоположную сторону под прямым углом.

Четырёхугольник

Сегодня мы рассмотрим геометрическую фигуру четырехугольник. Из названия этой фигуры уже понятно, что она имеет четыре угла. Однако мы обсудим и другие свойства.

Четырехугольник — это многоугольник, состоящий из четырех точек (вершин) и четырех отрезков (сторон), попарно соединенных этими точками. Площадь четырехугольника равна половине произведения его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Четырехугольник — это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой и последовательно соединены отрезками.

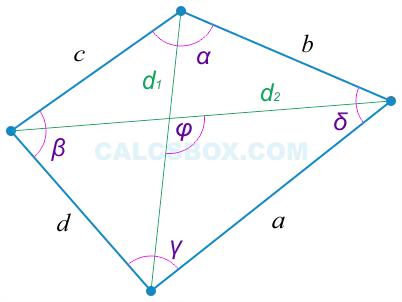
Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

Четырехугольник может быть:

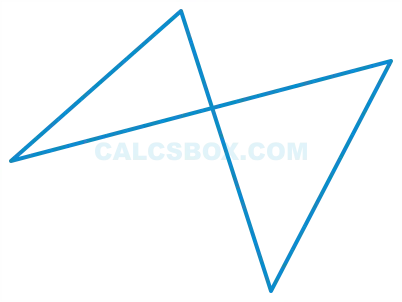
Единственный пересекающийся четырехугольник — это четырехугольник с точкой пересечения (показана синим цветом) по обе стороны.

Невыпуклые четырехугольники — это четырехугольники, один из внутренних углов которых превышает 180° (на рисунке выделен оранжевым цветом).

Сумма углов несамостоятельных четырехугольников всегда равна 360 градусам.

Четырехугольник и окружность

Четырехугольники с контуром, нарисованным вокруг окружности (окружность, вписанная в четырехугольник).

Основные характеристики очерченного четырехугольника:.

Четырехугольник может быть описан вокруг окружности только в том случае, если суммы противоположных длин равны.

Вписанный четырехугольник (круг, нарисованный вокруг четырехугольника).

Основные свойства вписанного четырехугольника:.

Четырехугольник может быть вписан в окружность только в том случае, если сумма противоположных углов равна 180 градусам.

Радиус четырехугольной окружности R с половиной периметра p и сторонами a, b, c и d определяется по формуле Парамешвары: r = (¼)*((a * b + c * d)*(a * c + b * d)*(a * d + b * c))/((p-a)*(p-b)*(p-c)*(p-d))^(½). Аналогия возникла благодаря индийскому математику XV века Ватасери Парамешваре.

Четырёхугольник

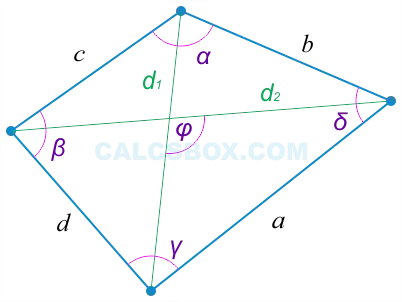
В этом уроке мы рассмотрим геометрические фигуры, такие как четырехугольники. Вводится понятие четырехугольника. Сформируйте представление о его верхней и боковых поверхностях. Вы узнаете, какие четырехугольники называются выпуклыми, а какие невыпуклыми. Мы также обсудим диагонали и периметры четырехугольника. Затем они узнают, что сумма углов выпуклого четырехугольника равна 360°. Он также закрепляет то, чему вы научились в практической части урока.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из набора, вам необходимо приобрести их в каталоге и добавить в свой личный стенд.

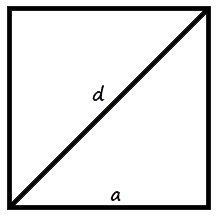
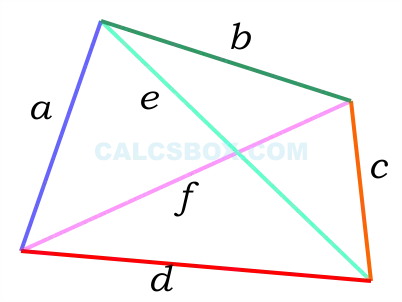
Конспект урока «Четырёхугольник»

В предыдущем уроке мы обсудили многоугольники. Помните, что многоугольник — это геометрическая фигура, состоящая из частей и внутренних областей. Точка А.₁, A₂, A₃ и т.д._n-1, A_n называется многоугольником, а вершины отрезка A₁A₂, A₂A₃,…, A_n-1A_n, A_n называемые ребрами многоугольника.

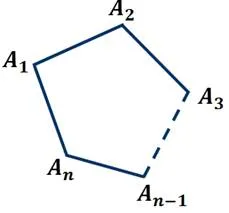
Многоугольник с n вершинами называется n-прямоугольником.

В этом уроке мы обсудим четырехугольники. Таким образом, четырехугольник — это геометрическая фигура, состоящая из четырех точек и четырех последовательных отрезков, соединяющих их.

Нет трех точек на одной прямой, и соединяющие их отрезки не пересекаются.

Точки A, B, C и D называются вершинами четырехугольника. А отрезки прямых AB, BC, CD и DA, соединяющие эти точки, называются сторонами четырехугольника.

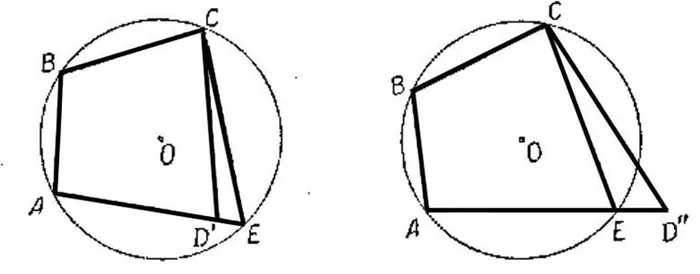
Давайте рассмотрим следующие элементы.

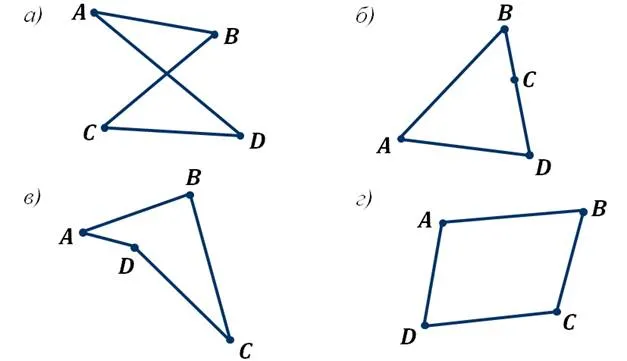
Каждая из них состоит из четырех точек и четырех частей, соединяющих эти точки в непрерывной последовательности. Обратите внимание, что первая фигура не является четырехугольником, так как отрезки AD и BC пересекаются. Следующая фигура имеет точки B, C и D на одной прямой и не является четырехугольной. Следующая фигура — четырехугольник. Это происходит потому, что ни одна из трех точек не лежит на одной прямой и их соединения не пересекаются. Последняя фигура также является четырехугольником, потому что ни одна из трех точек не лежит на одной прямой и их соединения не пересекаются.

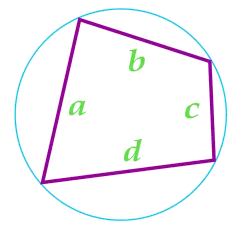
Вершины четырехугольника, принадлежащие одной и той же стороне, называются смежными. Например, вершины A и B и A и D являются смежными.

Вершины, которые не являются соседними, называются противоположными вершинами. Таким образом, в четырехугольниках A и C, B и D симметричны.

Стороны четырехугольника, начинающиеся от одной вершины, называются смежными. Например, BC и CD являются смежными.

Грани, не имеющие общей вершины, называются противоположными. Таким образом, AB и CD, AD и BC взаимозаменяемы.

Четырехугольники могут быть выпуклыми или невыпуклыми.

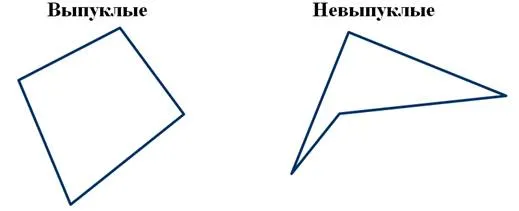
Выпуклые четырехугольники лежат по одну сторону от прямой, проходящей через две соседние вершины. Однако если четырехугольник лежит по обе стороны хотя бы одной прямой, проходящей через две соседние вершины, он является невыпуклым.

Отрезки, соединяющие противоположные вершины четырехугольника, называются диагоналями.

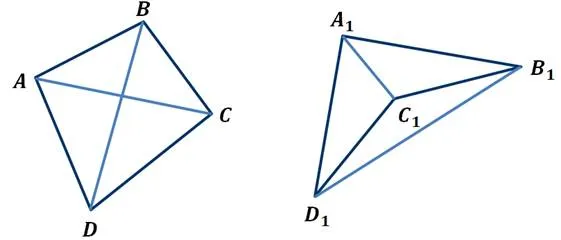
Так, в выпуклом четырехугольнике ABCD отрезки AC и BD являются диагоналями. Каждая диагональ делит этот четырехугольник на два треугольника.

У четырехугольника есть два противоположных угла, сумма которых равна ⌘ (⌘ displaystyle 180)<>^ \ \ \ \ \}} то такой четырехугольник является вписанным.

Площадь четырехугольника, заданного координатами

Тип площади четырехугольника на основе координат используется для вычисления площади координатной фигуры. В этом случае сначала необходимо рассчитать требуемую длину сторон. Сам тип может отличаться в зависимости от типа четырехугольника. Рассмотрим пример вычисления площади четырехугольника с помощью квадрата в системе координат XY.

Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле: Найдем одну из сторон, к примеру, AB : Подставим значения в формулу: Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:

Нахождение площади четырёхугольника различными способами и методами

Вы узнаете, как найти площадь четырехугольника, учитывая его диагонали и острые углы, образованные их пересечениями. Затем площадь четырехугольника вычисляется по формуле: s = 1/2 * d1 * d2 * sin (d1, d2).

Рассмотрим его пример. Пусть d1 = 15 см, d2 = 12 см, а угол между ними равен 30 градусам. Пусть S. S = 1/2 * 15 * 12 * sin30 = 1/2 * 15 * 12 * 1/2 = 45 см квадратных.

Теперь посмотрите на стороны и противоположные углы четырехугольника.

Пусть a, b, c и d — известные стороны многоугольника, а p — его периметр. Квадратный корень из формулы называется rad (от латинского radical). Формула для площади четырехугольника дается следующим образом (a, b) + (c, d))/ 2), где p = 1/2 * (a + b + c + d).

На первый взгляд, формула кажется очень сложной и изощренной. Однако здесь нет ничего сложного. Мы докажем это на примере. Рассмотрим данные нашей ситуации: α = 18 мм, β = 23 мм, γ = 22 мм, δ = 17 мм. Противоположные углы равны (a, b) = 0,5° и (c, d) = 1,5°. Сначала найдите длину полуокружности: p = 1/2 * (18 + 23 + 22 + 17) = 1/2 * 80 = 40 мм.

Теперь найдите квадрат синуса запятой противоположного угла: co s ^ 2 ((a, b) + (c, d)) / 2) = c o s ^ 2 (0,5 + 1,5) / 2 = c o s1 * c o s1 = (1/2) * (1/2) = 0,9996.

Эти данные заменяются формулой: s = rad((40-18)*(40-23)*(40-22)*(40-17)-18 * 23 * 22 * 17 * 0,97) = rad((22 * 17 * 18 * 23-18 * 23 * 22 * 17 * 1/4) * (1-0,9996)) = рад (154836 * 0,0004) = рад62 = 7 875 мм в квадрате.

Узнайте, как вычислить площадь с помощью конечных циклов и окружностей. При устранении этой проблемы рекомендуется приложить к действию план поддержки, но это требование не является обязательным.

Если у вас есть акроцикл и вам нужно найти площадь четырехугольника, формула будет такой: α = 16,5, α = 16,5, α = 16,5, α = 16,5, α = 16,5.

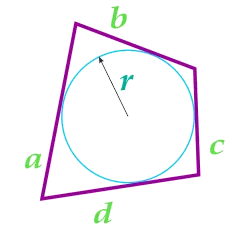
Рассмотрим другой пример: α = 16 метров, β = 30 метров, γ = 28 метров, δ = 14 метров, r = 6 метров. Подставляя цены в прессе, получаем

S = ((16 +30 + 28 + 14) / 2) * 6 = 44 * 6 = 264 кв. м.

Давайте теперь обсудим случай, когда окружность нарисована вокруг четырехугольника. Здесь можно использовать следующее уравнение

S = rad((p —a)*(p — b)*(p — c)*(p — d), где p — половина длины периметра. В этом случае значения сторон: α = 26 метров в десятичной дроби, β = 35 метров в десятичной дроби, γ = 39 метров в десятичной дроби, δ = 30 метров в десятичной дроби.

Сначала определим полудесятичную длину, p = (26 + 35 + 39 + 30) / 2 = 65 дециметров. Подставим найденную цену в формулу. Мы получаем:.

S = rad ((65-26)*(65-35)*(65-39)*(65-30)) = rad (39 * 30 * 26 * 35) = 1032 (округленно) десятичных.

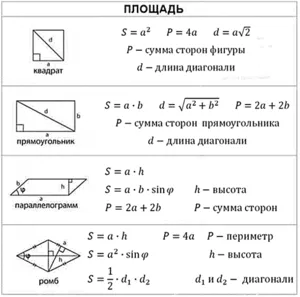
Квадрат, прямоугольник и другие параллелограммы

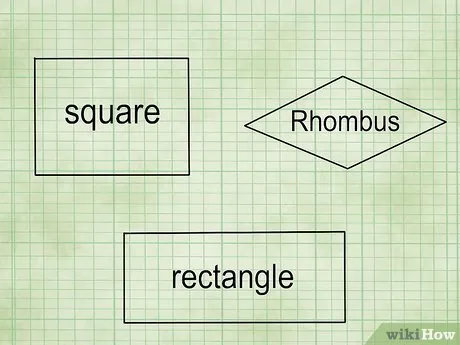
Определение прямоугольника. Прямоугольник — это четырехугольник с равными противоположными сторонами, параллельными друг другу. Квадраты, прямоугольники и ромбы — это прямоугольники.

• Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
• Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
• Ромб — это параллелограмм, у которого все стороны равны.

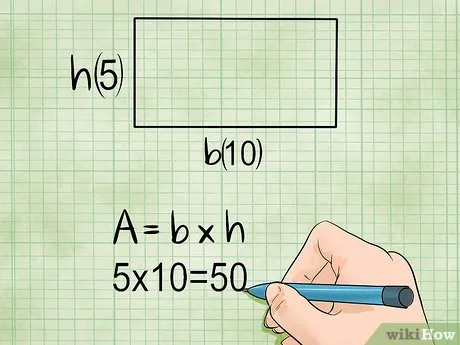
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона — считается высотой) и длину (длинная сторона — считается стороной, на которой проведена высота). Площадь прямоугольника равна произведению его длины и ширины.

• ‘ Площадь = длина х высота , или S = a х h .
• Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров .
• Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).

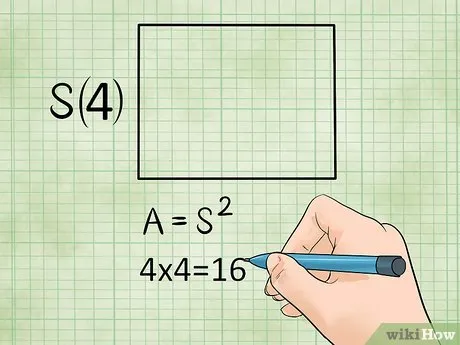
Площадь квадрата. Поскольку квадрат является частным случаем прямоугольника, используйте ту же формулу, что и для нахождения площади прямоугольника. Однако в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (т.е. умноженной на себя). 1

• Площадь = сторона х сторона , или S = a 2 .
• Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a 2 = 4 х 4 = 16 квадратных сантиметров .

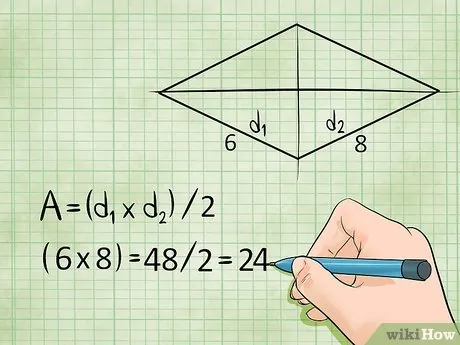
Площадь ромба равна его диагонали, деленной на 2. Диагональ — это часть ромба, соединяющая противоположные вершины. 2

• Площадь = (диагональ1 х диагональ2)/2 , или S = (d₁ ×x d₂)/2
• Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.

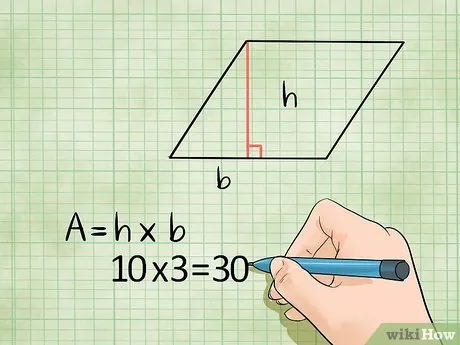
Площадь ромба также можно найти, умножив его стороны на высоту, приходящуюся на эту сторону. Однако не путайте высоту с прилегающей стороной. Высота — это линия, которая выходит из любой вершины ромба на противоположную сторону и пересекает противоположную сторону под прямым углом.

• Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров .

Площади двумерных фигур — это геометрические понятия, которые указывают на их числовые свойства или размер. В большинстве случаев они обозначаются буквой S. Она измеряется в квадратных метрах (см 2, м 2, и т.д.). Фигура с характеристикой S называется квадратом.

Найдите углы вписанного в окружность четырехугольника, если три угла(в последовательном порядке) относятся как 4 : 7 : 6?

Если три угла (последовательно) равны 4:7:6, найдите угол четырехугольника, записанного в круге.

Ответ Максимальная степень ответа.

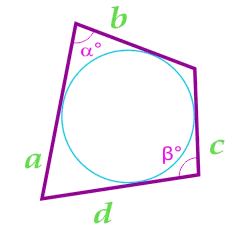
Четырехугольник может быть зарегистрирован в круге только в том случае, если сумма противоположных углов равна 180°.

4: 7: 6: x x конг угловых пар4 + 6 = 7 + x

Цикл составляет 360°.

А сумма отрезков, на которые он разделен, равна 10 + 10 = 20, шкала оценки отрезка

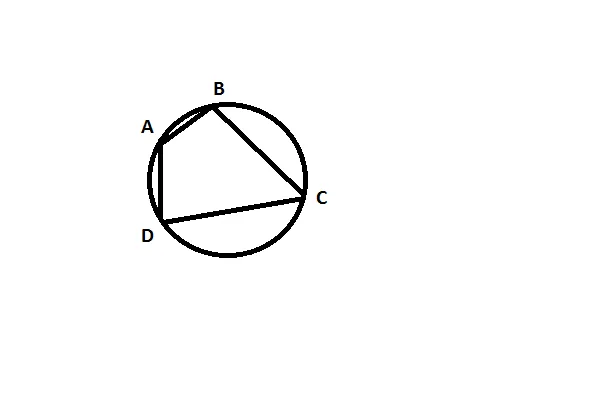
Четырехугольник ABCD вписан в окружность, угол А = 108 *, угол В = 70 * ?

Четырехугольник ABCD описан на окружности под углом a = 108 * и углом b = 70 *.

Найдите минимальное значение остальных углов.

Какой угол четырехугольника записан в круге, если три угла (в последовательном порядке) на этой странице связаны с категорией геометрии 4:7:6? Этот вопрос имеет те же трудности, с которыми сталкиваются учащиеся 5-9 классов. Здесь вы можете найти и обсудить правильный ответ и сравнить его с мнением других пользователей сайта. Используйте автоматический поиск на этой же странице, чтобы найти похожие вопросы и ответы к категории геометрия. Если вы не уверены в ответе, переформулируйте свой вопрос. Для этого нажмите кнопку вверху.

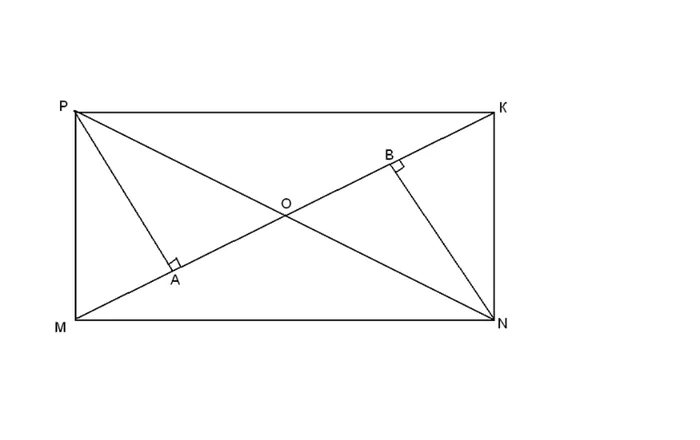
ДОКАЗАТЕЛЬСТВО: Предположим, что отрезки AC и BD пересекаются в точке o треугольника. aob = треугольник с первым знаком (угол aob, угол sod перпендикулярны, bo = od, ao = os, так как o — середина ac и ua) треугольник abc = треугольник SOD с первым знаком (ac — общий. …

AC = 16 + 2 = 18 (см) BC = 18-8 = 10 (см) p = 16 + 18 + 10 = 44 (см) Ответ: 44 см.

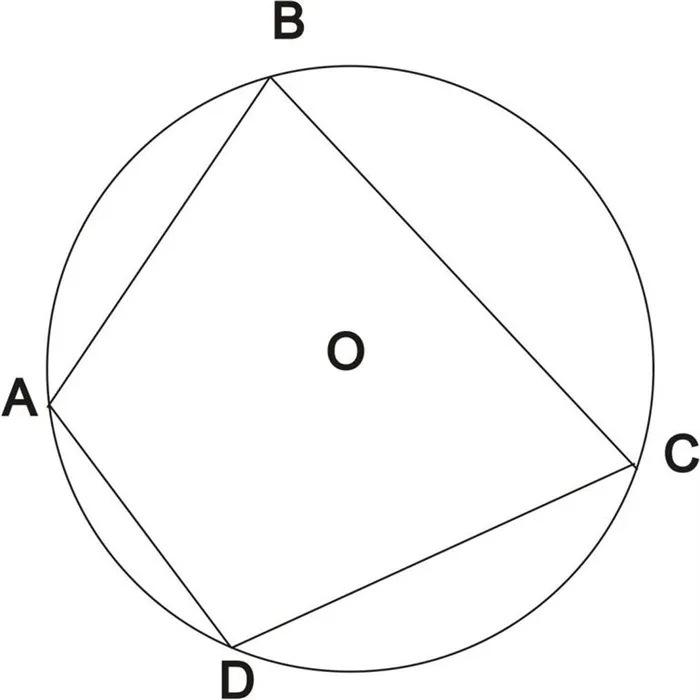
Да, так как это проекция, то возможно отображение.

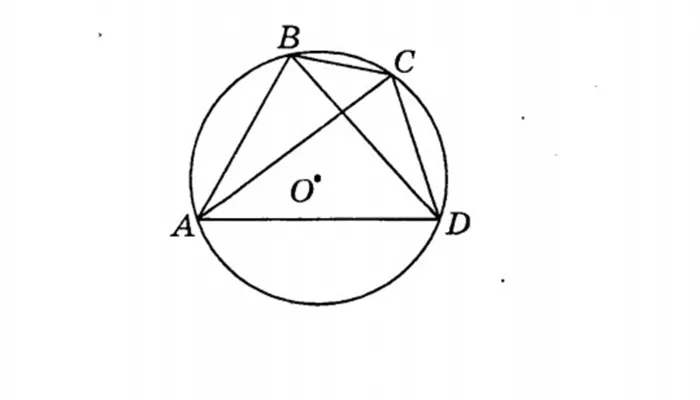
AC = AD + DC = 6 + 8 = 14. Спроектируйте CH, которая является высотой ABC. Это также высота треугольника ABD. SABC = 1/2 AC -BHBH = 2SABC /AC = 2-42 /14 = 6SABD = 1/2 AB -BH = 1 /2-6-6-6 = 18 кв.м. изд.

Невыпуклые четырехугольники — это четырехугольники, один из внутренних углов которых превышает 180° (на рисунке выделен оранжевым цветом).

Вписанный четырехугольник и его свойства (ЕГЭ 2022)

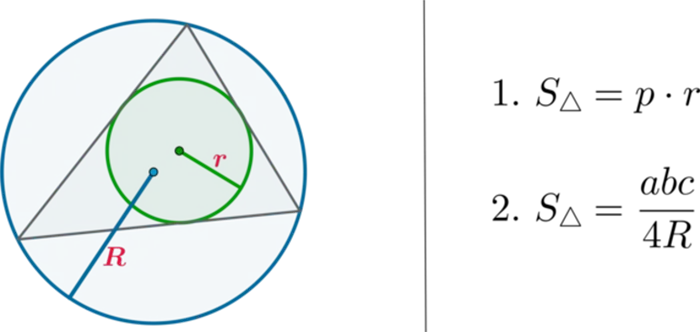
Оказывается, можно описать круг вокруг треугольника. Например, такой:

Вопрос: Могу ли я получить записанный четырехугольник?

Верно ли, что всегда существует круг, на котором сидят все четырехугольники всех четырех вершин?

Вписанный четырехугольник — коротко о главном

Если четырехугольник вписан в окружность, то сумма двух противоположных углов равна ߡ(ߡ displaystyle 180<>^\ круг \)

У четырехугольника есть два противоположных угла, сумма которых равна ⌘ (⌘ displaystyle 180)<>^ \ \ \ \ \}} то такой четырехугольник является вписанным.

Четырехугольник будет зарегистрирован как круг, только если сумма двух противоположных углов равна ⌘ (⌘ displaystyle 180), тогда четырехугольник будет зарегистрирован как круг.<>^\ circ \).

)<>^\ circ \).

Прямоугольник, вписанный в окружность, обязательно является прямоугольником, и его центр совпадает с точкой пересечения диагоналей.

Вписанный четырехугольник — определения и теоремы

Оказывается, это не так!

Не всегда можно записать четырехугольную окружность.

Существует очень важное условие:

Четырехугольник может быть зарегистрирован как круг, только если сумма двух противоположных углов равна ⌘ (⌘ displaystyle 180.<>^\ circ \).

В нашей диаграмме: ⌘ (⌘ displaystyle \ alpha + ⌘ beta = 180)<>^\ круг \)

Смотрите, углы \(\ displaystyle \ alpha \) и \(\ displaystyle \ beta \) противоположны друг другу и поэтому противоположны. Как насчет углов ⌘ (⌘ displaystyle \ varphi \) и ⌘ (⌘ displaystyle \ psi \)? Разве они не противоположны?

Углы ⌘ (⌘ displaystyle \ alpha \) и ⌘ (⌘ displaystyle \ beta \) можно заменить углами ⌘ (⌘ displaystyle \ varphi \) и ⌘ (⌘ displaystyle \).

Главное — найти два противоположных угла четырехугольника. Сумма этих углов равна ᢙ (ᢙ displaystyle 180).<>^\ circ \).

Два других угла добавляются к \(⌘ displaystyle 180)<>^ \ \ \ circ \). Вы мне не верите, давайте проверим.

\ \ displaystyle \ alpha + \ beta = 180)<>^ \ circ \). Помните ли вы, чему равна сумма всех четырех углов четырехугольника? Определенно, ዄ (ዄ displaystyle 360).<>^\ circ \).

Следовательно, \(\ displaystyle \ альфа + \ бета + \ варфи + \ пси = 360<>^ \ circ \) — всегда! \ \ \ displaystyle 180<>^\ круг \)

Однако 팀 (팀 displaystyle \ alpha + \ beta = 180<>^ \ circ \), -> ᢙ (ᢙ displaystyle \ varphi + \ psi = 360)<>^ \ circ -180<>^ \ окружность = 180<>^ \ circ \)

Поэтому хорошо запомните это.

Если четырехугольник вписан в окружность, то сумма любых двух противоположных углов равна ⌘ (⌘ displaystyle 180<>^ \\\\ circ \\\ circ \\\ circ \\\\ }

Если четырехугольник имеет два противоположных угла, то сумма любых двух противоположных углов равна ⌘ (⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180).<>^ \\\\ circ \\) Далее, четырехугольник вписан.

Смотрите чек чуть ниже.

А пока давайте посмотрим, к чему приведет этот примечательный факт. Вписанный четырехугольник — это четырехугольник, сумма противоположных углов которого равна ⌘ (⌘ displaystyle 180).<>^\ circ \).

Теперь возникает вопрос, например, можно ли нарисовать круг вокруг прямоугольника?

Вписанный параллелограмм

Сначала попробуйте применить «научный метод».

Это не работает. Теперь давайте применим наши знания.

Предположим, что вам каким-то образом удалось вписать круг в прямоугольник ⌘ (⌘ displaystyle ABCD \). Тогда нам нужно сделать следующее: \(\ displaystyle \ alpha + \ beta = 180)<>^ \ \ \ circ \), поэтому: \(\ displaystyle \ угол B + \ угол D = 180)<>^\ circ \).

Вспомним свойства прямоугольников. Каждый прямоугольник имеет равный и противоположный угол.

Следовательно, 퓡 (퓡 displaystyle \ угол B = 퓡 угол D 퓡).

\ displaystyle \ left \< \begin\angle B=\angle D\\\angle B+\angle D=180<>^ \circ \ end \ right.\) → 섹 (섹 displaystyle \ left \)< \begin\angle B=90<>^ \circ\\\\ угол D=90<>^ \ \ displaystyle \ left ^ \ displaystyle \ right).

Как насчет углов ⌘ (⌘ displaystyle A \) и 섹 (섹 displaystyle C \)?