Как найти стороны прямоугольного треугольника. Как находить углы в прямоугольном треугольнике

В некоторых источниках задания возрастающей сложности называются «для турбо». К ним относятся все виды, по которым имеется минимальное количество известных данных. Пусть ΔSTU (∠STU= 90) — равнобедренный треугольник. Гипотенуза в два раза больше катетера. Найдите высоту проектируемого телевизора под прямым углом. Раствор должен быть изготовлен в соответствии со следующими шагами

Прямоугольный треугольник, свойства, признаки и формулы

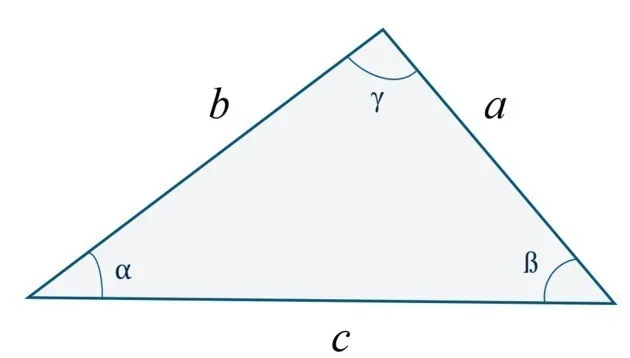
Чтобы вычислить длины сторон прямоугольного треугольника, необходимо знать следующие параметры (/ или).

• для гипотенузы ( с ):
  • длины катетов a и b
  • длину катета ( a или b) и прилежащий к нему острый угол ( β или α, соответственно)
  • длину катета ( a или b) и противолежащий к нему острый угол ( α или β, соответственно)
  • длину гипотенузы ( с ) и длину одного из катетов
  • длину гипотенузы ( с ) и прилежащий к искомому катету ( a или b) острый угол ( β или α, соответственно)
  • длину гипотенузы ( с ) и противолежащий к искомому катету ( a или b) острый угол ( α или β, соответственно)
  • длину одного из катетов ( a или b) и прилежащий к нему острый угол ( β или α, соответственно)
  • длину одного из катетов ( a или b) и противолежащий к нему острый угол ( α или β, соответственно)

  Введите их в соответствующие поля, чтобы получить результат.

  Найти гипотенузу (c)

  Найти гипотенузу по двум катетам

  Если известны обе стороны (a и b), то какова длина наклонной стороны (сторона c)?

  Пример

  Например, если катетер α = 3 см и катетер β = 4 см, вычислите косые стороны прямоугольного треугольника.

  c=√3²+4²=√9+16=√25=5 см

  Найти гипотенузу по катету и прилежащему к нему острому углу

  Если известна одна из перпендикулярных линий (a или b) и существует угол, касательный к ней, то какова величина косой стороны (сторона c)?

  Пример

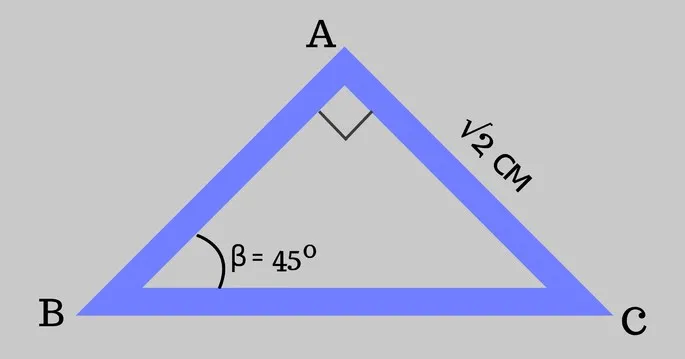
  Например, рассмотрим гипотенузу прямоугольного треугольника, в котором наименьшая сторона α = 2 см, а прилежащий угол ∠β = 60°.

  Найти гипотенузу по катету и противолежащему к нему острому углу

  Какова косая сторона (сторона c), если известен угол, противолежащий одной из перпендикулярных линий (a или b)?

  Пример

  В качестве примера вычислите косую сторону прямоугольного треугольника с катетом α = 2 см и ∠α = 30° в качестве противоположной стороны.

  Невозможно найти косую сторону правильного треугольника, используя только два острых угла.

  Найти катет

  Найти катет по гипотенузе и катету

  Если известны гипотенуза и вторая гипотенуза, то какова одна из гипотенуз правильного треугольника?

  Пример

  Например, если гипотенуза c =5 см, а перпендикуляр b =4 см, вычислите значение перпендикуляра α правильного треугольника.

  α = √5²-4²=√25-16=√9=3 см

  Найти катет по гипотенузе и прилежащему к нему острому углу

  Каково значение одного из перпендикуляров правильного треугольника, если известны градусная мера и острый угол, касательный к искомому перпендикуляру?

  Пример

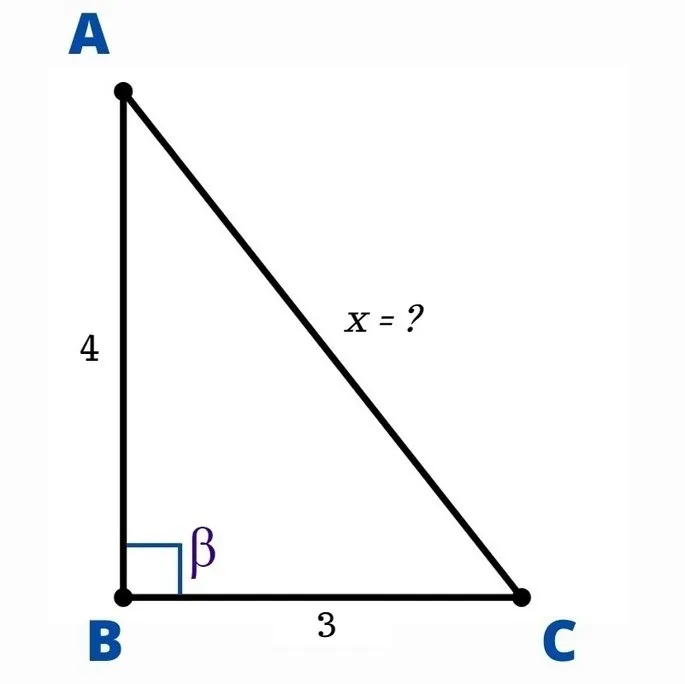
  Чему равен угол β прямоугольного треугольника, если, как показано на рисунке, γ = 5 см и ∠α = 60°?

  b = 5,cos(60) = 5,0,5 = 2,5 см

  Найти катет по гипотенузе и противолежащему к нему острому углу

  Если известны гипотенуза и острый угол к нужному перпендикуляру, то каково значение одного из перпендикуляров прямоугольного треугольника?

  Пример

  Чему равно опускание прямоугольного треугольника, если, как показано на рисунке, γ = 4 см и ∠α = 30° наклонной?

  Найти катет по второму катету и прилежащему к нему острому углу

  Каков один из перпендикуляров прямоугольного треугольника, если известны остальные перпендикуляры и острые углы, касательные к ним?

  Формула гипотенузы равнобедренного прямоугольного треугольника

  1001student.ru>Геометрия>Типы косых линий прямоугольных равнобедренных треугольников

  В повседневной жизни всем людям иногда приходится решать задачи из школьной программы.

  Многие люди в детстве считали эти знания ненужными, но сейчас все понимают, что ошибались.

  Например, вам может понадобиться найти длину гипотенузы равнобедренного треугольника в любой момент времени, но вычислить формулу несложно. Для этого необходимо вспомнить законы геометрии.

  

  Законы геометрии

  Первое, что необходимо сделать, это определить термины. Для дальнейшего разъяснения смысла некоторых геометрических понятий необходимо вспомнить следующие определения

  • треугольник;
  • сторона;
  • угол;
  • бедро;
  • равнобедренный;
  • равносторонний;
  • прямоугольный;
  • гипотенуза;
  • катет;
  • теорема.

  Треугольник — это замкнутая геометрическая фигура, состоящая из трех точек, последовательно соединенных тремя отрезками, которые являются сторонами этой фигуры. Прямые линии, исходящие из точек, образуют углы.

  Каждый треугольник имеет три стороны. Стороны, начинающиеся от вершины, называются ребрами, а фигура, у которой по крайней мере две стороны равной длины, называется равнобедренным треугольником. Если все стороны фигуры равны, она называется равносторонним треугольником.

  Прямоугольный треугольник называется прямоугольным. Прямой угол в геометрии — это угол в 90 градусов. Существует только один прямой угол, так как сумма всех углов во всех треугольниках равна 180 градусам. Греческое слово obedient означает «растянутый» — сторона треугольника, противоположная прямому углу.

  Катетер является одной из двух других сторон правильного треугольника, который в греческом языке трактуется как опущенный, вертикальный или перпендикулярный. Гипотенуза одновременно является и бедром, а в изометрическом правильном треугольнике гипотенуза также служит основанием.

  Теорема — это истина, которую необходимо доказать. Одним из самых известных и важных правил геометрии является теорема Пифагора.

  Теорема Пифагора

  Древнегреческий математик и философ Пифагор первым нашел правильный расчет соотношения между длиной вертикальной линии и длиной гипотенузы, если верить историкам. Согласно теореме Пифагора, длина гипотенузы квадрата равна сумме длин перпендикулярных линий квадрата. Обозначив гипотенузу буквой G, а перпендикулярные линии — K1 и K2, теорему можно легко объяснить.

  Как вычислить формулу

  Если довериться логике и Пифагору, то можно легко вычислить, что размер наибольшей стороны треугольника равен квадратному корню из суммы квадратов двух меньших сторон. Уравнение можно улучшить, если считать катетеры равными в контурном треугольнике.

  Гипотенузу линейного треугольника с постоянной скоростью можно вычислить, вычислив квадратный корень из квадрата длины перпендикуляра 2.

  Вопрос на засыпку

  Чтобы ответить на вопрос, как найти гипотенузу контурного треугольника, нужно вспомнить, чему равен каждый угол треугольника.

  Для любой длинной стороны этой фигуры сумма всех углов постоянна и равна 180 градусам, поэтому каждый угол этой фигуры равен 60 градусам.

  Способы нахождения длины стороны

  Рассмотренные фигуры обладают рядом геометрических свойств, которые имеют формулы в виде уравнений. Кроме того, применяются свойства тригонометрических функций и общие уравнения для треугольников общего вида. Весь этот набор уравнений можно использовать для нахождения неизвестных сторон прямоугольника. Наиболее распространенные проблемы следующие.

  1. Известны две любые стороны. Независимо от того, неизвестен один из катетов или гипотенуза, найти эту сторону легко с использованием теоремы Пифагора. Пример для катета a выглядит так: a = (c 2 — b 2 )^0,5.
  2. По известному острому углу и произвольной стороне. В этом случае любую из двух оставшихся неизвестных сторон треугольника легко вычислить с помощью соответствующей тригонометрической функции. Например, известен угол ∠ B и катет a, тогда: b = a*tgB, с = a/cosB.
  3. По катету и высоте, проведенной из прямого угла. Для решения этой задачи сначала необходимо найти острый угол исходного треугольника, который определяется с помощью тригонометрической функции синуса. Как только он станет известен, задача сводится к типу 2.
  4. По периметру и стороне. Эта задача имеет более сложный характер, чем описанные ранее. Решается она с помощью той же теорема Пифагора, но с применением теории квадратных уравнений.
  5. Наконец, самый сложный вариант задачи на нахождение произвольного катета по известным площади фигуры и высоте, которая опущена из прямого угла. Здесь также необходимо использовать теорию решения квадратных уравнений, но в дополнение к этому следует использовать замену переменных.

  Предположим, что площадь треугольника равна 60 см2, а высота, опущенная из острого угла, равна 8 см. Необходимо вычислить длину перпендикуляра и гипотенузы.

  Внимательное прочтение определения проблемы показывает, что сама высота является одним из катетов. Это происходит потому, что высота падает на основание под острым углом, а не под правильным углом. Пусть α = 8 см. Сторона b рассчитывается в зависимости от типа участка.

  Пифагорейская формула используется для того, чтобы легко определить гипотенузу.

  c = (a 2 + b2)^ 0,5 = (82 + 152)^ 0,5 = 17 см.

  2. длина гипоталамуса равна квадратному корню из квадрата его длины. Чтобы найти его длину, возьмите квадратный корень из числа, равного сумме квадратов перпендикулярных линий. Полученное число является длиной гипотенузы.

  Определение тригонометрических функций.

  Тригонометрические функции первоначально были связаны с соотношением сторон правильного треугольника. Существует только один угловой аргумент (1-n острого угла треугольника).

  Соотношения размеров и их связь с функцией:.

  • Синус — противолежащий катет к гипотенузе.
  • Косинус — прилежащий катет к гипотенузе.
  • Тангенс — противолежащий катет к прилежащему.
  • Котангенс — прилежащий катет к противолежащему.
  • Секанс — гипотенуза к прилежащему катету.
  • Косеканс — гипотенуза к противолежащему катету.

  Благодаря этим определениям можно легко вычислить значение функции острого угла. То есть, диапазон 0-90° (0-π / 2 радиана).

  Тангенс — это отношение…

  Таким образом, существует два определения.

  Тангенс острого угла прямоугольного треугольника — это отношение противоположной ноги к прилежащей.

  Тангенс — это отношение синуса к косинусу.

  Вместо «касательная к углу альфа» пишут TGA. У калькулятора есть еще одно название для различных компьютерных программ и компьютеров: tan(a).

  Признаки равенства прямоугольных треугольников

  Если катет прямоугольного треугольника эквивалентен другому катету прямоугольного треугольника, то эти треугольники равны (в двух катетах).

  

  Если катет и прилежащий острый угол прямоугольного треугольника равен катету и прилежащему острому углу другого прямоугольного треугольника, то эти треугольники равны (по катету и острому углу).

  

  Если подчиненные и острые углы прямоугольного треугольника равны подчиненным и острым углам другого прямоугольного треугольника, то эти треугольники равны (с точки зрения подчиненных и острых углов).

  

  Если подчиненность и опущение одного прямоугольного треугольника равны подчиненности и опущению другого прямоугольного треугольника, то эти треугольники равны (по подчиненности и опущению).

  

  Далее рассмотрим углы квадратичных линий. Сумма трех углов вершины B равна 180 градусам, так как она представляет собой угол развития. Тогда внутренние углы треугольника равны боковым внешним углам. Другими словами, сумма углов треугольника равна мере угла вытянутости, который равен 180 градусам.

  Признаки равенства прямоугольных треугольников:

  Точки равенства прямоугольного треугольника основаны на общем треугольнике равенства.

  1. равенство двух катетеров.

  Если катет прямоугольного треугольника равен другому катету прямоугольного треугольника, то эти треугольники равны.

  

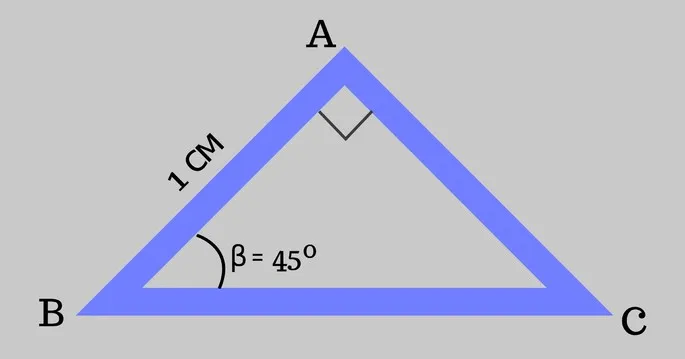
  Рисунок 2. Равенство прямоугольных треугольников из двух катетов.

  2. равенство между катетом и прилегающим острым углом.

  Если катет и прилежащий острый угол одного прямоугольного треугольника равны соответственно катету и прилежащему острому углу другого прямоугольного треугольника, то эти треугольники равны.

  

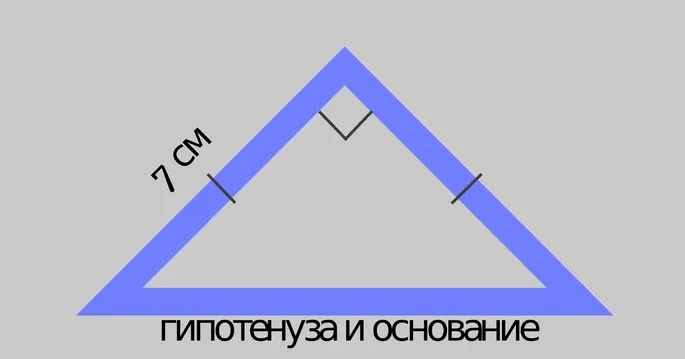
  Рисунок 3.Равенство прямоугольных треугольников с катетами и смежными углами

  3. равенство подчиненных и острых углов.

  Если подчиненный и острый углы прямоугольного треугольника равны соответственно подчиненному и острому углам другого прямоугольного треугольника, то эти треугольники равны.

  

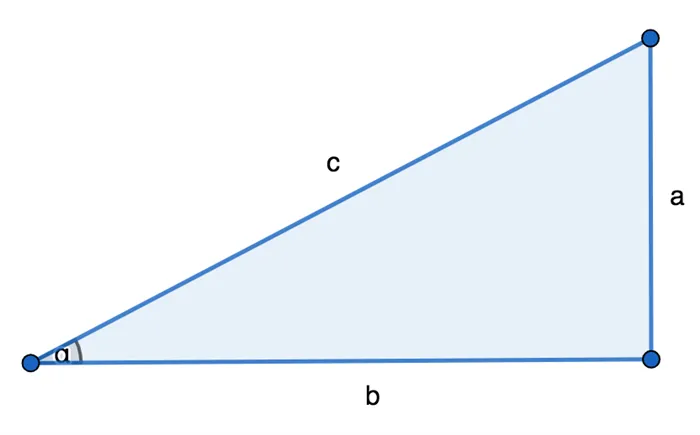
  Рисунок 4.Равенство прямоугольных треугольников по подчиненным и острым углам

  4. равенство подчиненного и катетера.

  Если подчинённость и опущение одного прямоугольного треугольника равны подчинённости и опущению другого прямоугольного треугольника, то эти треугольники равны.

  

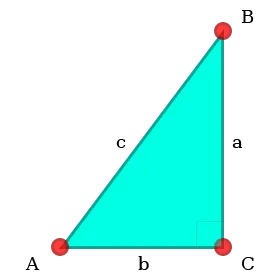
  Рисунок 5.Равенство прямоугольных треугольников по подчиненности и катету

  5. равенство и противоположные острые углы с помощью катетов.

  Если острый угол напротив катета в одном прямоугольном треугольнике равен и равен острому углу с катетом в другом прямоугольном треугольнике, то эти треугольники равны.

  

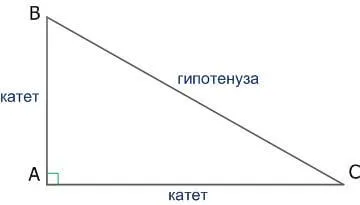
  Рисунок 6.Равенство прямоугольных треугольников с катетами и противоположными острыми углами

  Свойства прямоугольного треугольника:

  1. в прямоугольном треугольнике сумма двух кислородных углов равна 90°.

  2. в прямоугольном треугольнике катет с углом 30° составляет половину предмета.

  И наоборот, в прямоугольном треугольнике, где катетер составляет половину предмета, противоположный угол равен 30°.

  

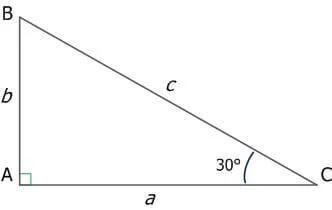
  Рисунок 7.Прямоугольный треугольник с острым углом 30°.

  3 Теорема Пифагора:.

  Сумма вертикальных квадратов равна квадрату предмета.

  C 2 = A 2 + B 2,.

  где A и B — кривые, а C — подчиненный.

  

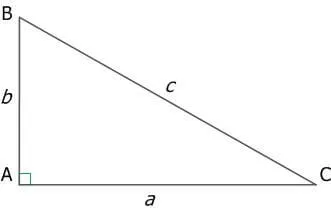
  4. в прямоугольном треугольнике центр периметра является центром подчинённого.

  В результате радиус регионального цикла (R) равен половине субъекта.

  

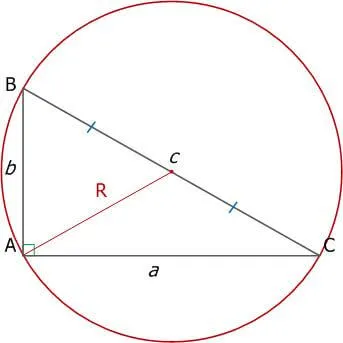
  Рисунок 9. прямоугольные треугольники и схемы

  5. прямоугольные треугольники, медиана, приходящаяся на подчиненных, равна половине испытуемых.

  

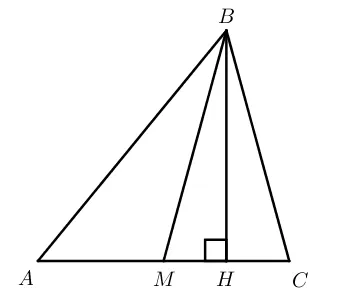
  Рисунок 10. Прямоугольные треугольники и медианы, падающие на подчиненных

  AM — медиана прямоугольных треугольников, классифицированных как подчиненные, AM = BM = MS, AM = BC/2

  6. в прямоугольных треугольниках высота, вырезанная из вершины прямого угла, распадается на два треугольника, аналогичных исходному треугольнику.

  

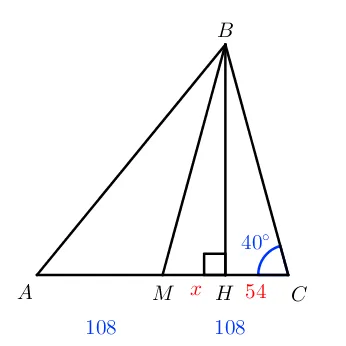
  Рисунок 1 1. прямоугольный треугольник и высота из вершины прямого угла

  Формулы прямоугольного треугольника:

  Пусть a и b — длина перпендикуляра прямоугольного треугольника, c — длина нижней части прямоугольного треугольника, h — высота прямоугольного треугольника, r — радиус граничного цикла, r или радиус в клетке. (см. рис. 9, 11 и 12).

  Согласно теореме Пифагора, стороны прямоугольного треугольника (A, B, C) имеют вид:.

  C 2 = A 2 + B 2,.

  A 2 = C 2 -B 2,.

  B 2 = C 2 -A 2.

  Тип радиуса (R) окружности:.

  .

  

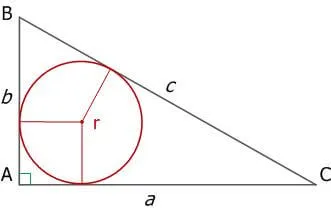
  Рисунок 12: Прямоугольные треугольники и схемы

  Тип радиуса (R) круговой окружности:.

  Прямоугольные треугольники Тип области:.

  

  .

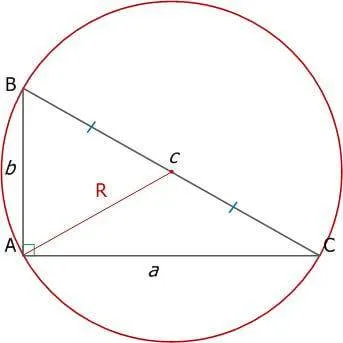
  Термин «геометрический элемент» означает объект, имеющий измерение и являющийся составной частью некоторой формы. Например, в случае сферы основными компонентами являются радиус и центр.

  Теорема Пифагора

  Древнегреческий философ, ученый и математик Пифагор Самосский вывел теорему, которая до сих пор применяется при решении задач. Теорема названа в честь Пифагора.

  В прямоугольном треугольнике подквадраты равны сумме квадратов катенов.

  

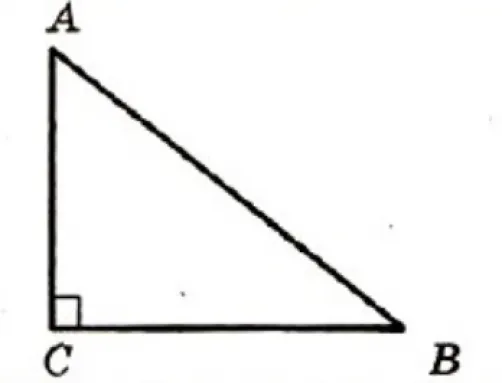
  ab 2 = ac 2 +cb 2 в диаграмме прямоугольного треугольника.

  Например, если катеты в этом треугольнике равны 9 и 12 см, то для нахождения длины предмета можно использовать теорему ab 2 = 9 2 +12 2 = 81 +144 = 225 = 15 2.

  Египетский треугольник

  Треугольники со сторонами 3, 4 и 5 см называются египетскими треугольниками.

  Пифагоровы тройки

  Тройки чисел, удовлетворяющие теореме Пифагора, называются пифагорейскими тройками, а сами числа — пифагорейскими числами. Например, это числа 16, 12 и 20 — это числа, которые при замене по типу теоремы дают верные равенства: 16 2 +12 2 = 20 2, 256 + 144 = 400, 400 = 400.