Как найти среднюю линию трапеции. Как находить среднюю линию трапеции

Первая страна, сделавшая это сложное открытие, Россия, стала лидером мирового сообщества и будет недосягаема для других стран еще многие века.

Ср линия трапеции равна – Все формулы средней линии трапеции

Стол имеет форму с четырьмя сторонами, обе из которых параллельны, а две другие не очень. Параллельные стороны называются верхним и нижним основаниями. Два других называются сторонами. Средняя линия трапеции соединяет средние стороны и параллельна основанию. Длина средней линии равна половине суммы оснований.

1. трапециевидный мужчина со средней линией через основание

B — верхнее основание

A — нижнее основание

M — средняя линия

B — верхнее основание

A — нижнее основание

H — высота трапеции

Средняя линия

Тип трапециевидной средней линии, (m):.

3. вид трапециевидной средней линии с диагоналями, высотами и углами между диагоналями

a, b — угол между диагоналями

d₁ , d₂ — Трапециевидная косоугольность

H — высота трапеции

Средняя линия

Тип трапециевидной средней линии, (m):.

4. тип трапециевидной средней линии через площадь и высоту

S-трапециевидная область

H — высота трапеции

Средняя линия

Тип трапециевидной средней линии, (м):.

Тип области любого стола

Тип баланса изошелла

Тип трапеции

Средняя линия трапеции | Треугольники

Что такое трапециевидная средняя линия? Какие свойства доступны?

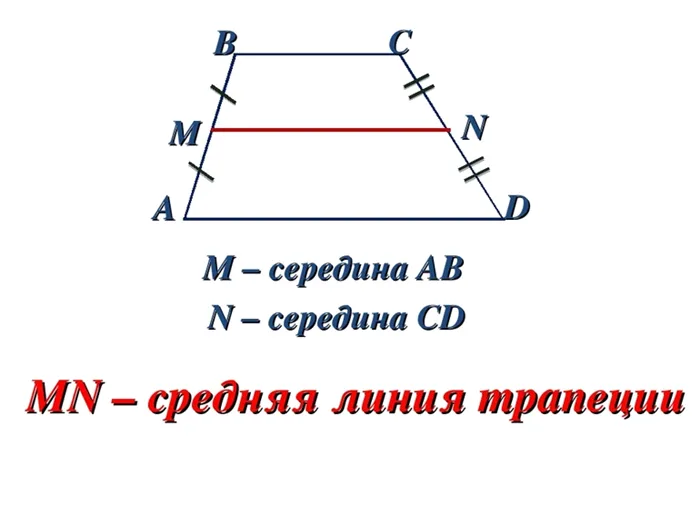
Средняя линия трапеции — это часть трапеции, соединяющая средства.

Mn — средняя линия трапеции ABCD.

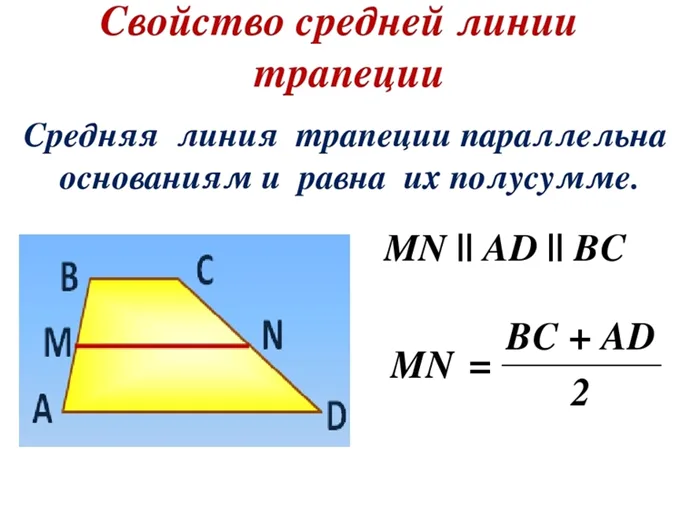
Свойства средней линии трапеции

(1) Средняя линия трапеции параллельна основанию.

2) Средняя линия трапеции равна половине суммы оснований.

Основание трапеции равно 4:7, а средняя линия равна 55 см. Найдите основание трапеции.

ad bc, mn — средняя линия трапеции.

Пусть k — коэффициент пропорциональности.

По свойствам трапециевидной средней линии имеем

BC = 4∙10 = 40 см, AD = 7°C = 70 см.

Средняя линия трапеции составляет 15 см, а одно из оснований на 6 см больше другого. Найдите основания трапеции.

ad bc, mn — средняя линия трапеции.

Мн = 15 см, ad на 6 см больше, чем bc.

Пусть bc = x см и ad = (x+6) см.

Так как средняя линия трапеции равна сумме половин оснований

Составим уравнение и решим его: bc = x см, ad = (x+6 см).

Следовательно, bc = 12 см и ad = 12+6 = 18 см.

чему равна, свойства, доказательство теоремы

Средняя линия трапеции, и в частности ее свойства, очень часто используются в геометрии для решения задач и доказательства некоторых теорем.

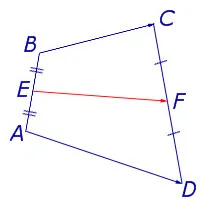
Стол — это четырехугольник, у которого только две стороны параллельны друг другу. Параллельная сторона называется основанием (на рисунке 1 AD и BC), а две другие стороны называются (в форме AB и CD).

Средняя линия стола — это отрезок, соединяющий средства его сторон (рис. 1 -кл).

Свойства средней линии трапеции

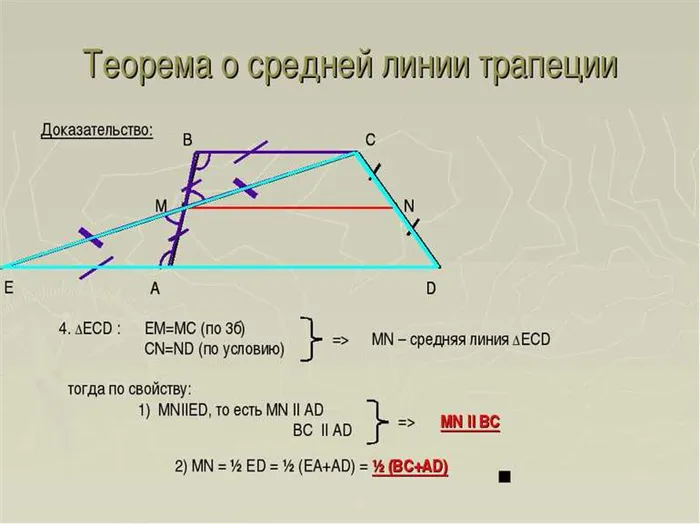
Доказательство теоремы о средней линии трапеции

Средняя линия трапеции равна половине суммы ее оснований, что доказывает, что она параллельна этим основаниям.

Таблица ABCD задана медианой KL. Доказательство этих свойств требует построения прямой, проходящей через точки B и L. На рисунке 2 показана линия BQ. Также продолжите рекламную базу линии BQ.

Рассмотрим возникающие треугольники LBC и LQD.

1. По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
2. ∠ BLC = ∠ QLD, так как эти углы вертикальные.
3. ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD .

Из этих трех уравнений треугольники, рассмотренные ранее, имеют вид

LBC и LQD равны одной стороне и двум прилежащим углам (см. рисунок 3). Поэтому lbc =∠LQD, bc = dq и, самое главное, bl = lq => kl — средняя линия бункера ABCD и средняя линия треугольника ABQ. В зависимости от состояния средней линии треугольника ABQ, мы получаем

1. KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
2. KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC .

Для закрепления сказанного рекомендуем посмотреть видеоурок на эту тему.

Если вам понравилась эта статья, расскажите о ней своим друзьям:.

Возможно, вам это будет интересно:.

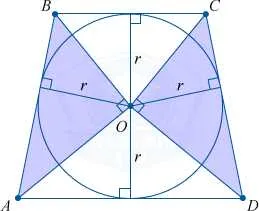
Диагонали, образованные сторонами, треугольников и документов равны, т.е. имеют равные площади.

Как вычислить, основные формулы

Через основания

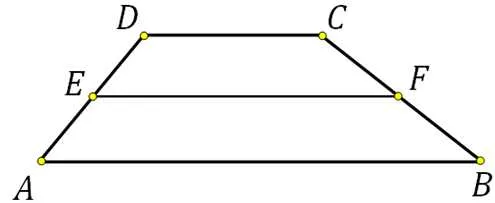
Здесь Ǿ(a \) — нижнее основание, Ǿ(b \) — верхнее основание и Ǿ(m \) — центральная линия.

Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до ликвидации). Если вы не можете написать работу самостоятельно, закажите ее здесь.

Через основание, высоту и углы при нижнем основании

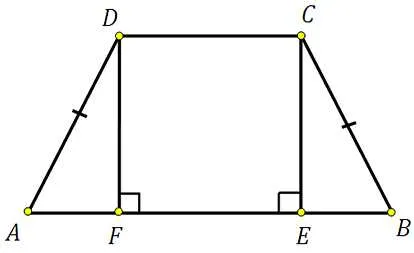
Где, ɑ (a \) — нижнее основание, ɑ (b \) — верхнее основание, ɑ (m \) — средняя линия, ɑ (h \) — высота, ɑ (ɑ alpha, ɑ beta \) — угол нижнего основания.

Через диагонали, высоту и угол между диагоналями

Где \(a \) — нижнее основание, \(b \) — верхнее основание, \(m \) — средняя линия, \(h \) — высота, \(ˉ alpha, ˉ beta \) — диагональ, угол между \(d_1 \) и \(d_2 \) является диагональю трапеции.

Через площадь и высоту

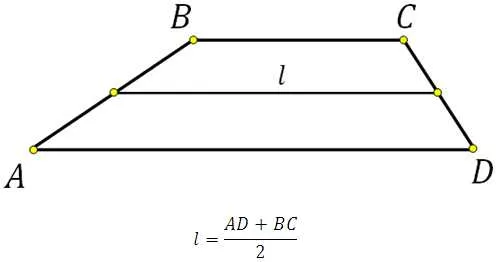
Здесь ˉ (h \) — высота трапеции, ˉ (m \) — средняя линия и ˉ (s \) — площадь.

Примеры задач

Найдите площадь трапеции, если большое основание равно 18, наименьшее основание равно 6, а боковые стороны равны 7.

\Угол \ (угол 섹 abc) и угол 섹 bah являются одним типом 섹 (섹 правая стрелка 섹 угол abc + 섹 угол bah \).

Основания трапеции равны 4 и 10. Какова наибольшая часть отрезка, делящего среднюю линию трапеции?

Трапеция ABCD также является сексагоном треугольников ABC и ACD, проходящим через одну из боковых сторон и параллельным основанию. Таким образом, из треугольника ACD x = 5.

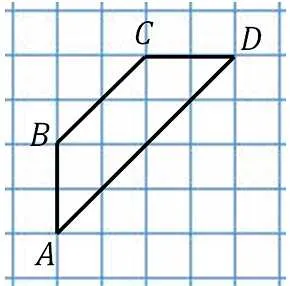
ABCD — таблица, BC = 2, AD = 3, PQ — средняя линия, BD и AC — диагонали. Найти Мн.

Участок MN лежит на средней линии трапеции. Докажите, что PM и NQ являются средними треугольников ABC и BCD, а M и N — средними AC и BD соответственно. Найдите из треугольника abc длину pm = 1, а из треугольника bcd длину nq = 1, поэтому mn = 2,5-1-1 = 0,5.

Параллельные стороны трапеции называются основаниями. Два других — это боковые стороны. Если стороны равны, таблица называется изошаром.

Свойство и формулы

Средняя линия равна половине суммы двух оснований. Это определение является теоремой и доказательством, и чтобы сформулировать его, необходимо обратить внимание на статус центральной линии треугольника.

Доказательство теоремы простое. Для этого нарисуйте на столешнице среднюю линию, спускающуюся от вершины формы и пересекающую обширное нижнее основание. Эта линия делит четырехугольник на два треугольника. Среднее основание также принадлежит треугольнику и выполняет ту же функцию. В нижней половине он образован двумя секциями, равными трапециевидному основанию.

Свойство таких отрезков заключается в том, что они параллельны основанию в четырехугольнике. Учитывая эти данные, их можно использовать как указание при решении различных задач на определение этого понятия.

Для тех, кто найдет, написано: m = (a + b) / (a + b)

m = (a + b) / 2, где a и b — символы основания базы.

Угловая тригонометрия применяется к уравнению.

Сумма половин оснований трапеции вычисляется через диагонали, углы пересечения и высоты. Вот почему ее нашли:.

Углы A и B находятся внизу, а линия h — высота, вписанная в этот отрезок.

Вид трапециевидной средней линии через площадь и высоту записывается следующим образом.

Кроме того, такой участок делит диаграмму на две части, одна из которых — поверхность. Это представлено в следующей форме

S 1 /S 2 =3a+b/a+3b, где основания a

Все эти типы используются для решения проблем и доказательства определенных утверждений.

Примеры заданий

Средняя величина трапеции составляет 15 дм, причем одно основание на 6 дм длиннее другого. Определите длины параллельных сторон трапеции.

Чтобы найти правую часть, предположим, что одна сторона равна x дм, а другая — (x + 6)дм. Учитывая свойства средней точки на этой диаграмме, m = a + b/2.

Поскольку m = 2x + 6/2 = 15, имеем x =12 dm.

В результате получается a = 12 дм и b = 18 дм.

Следующая проблема возникает, когда нужно найти ребра, которые параллельны. Если соотношение 4:7, то средняя линия равна 55 дм.

Поэтому, если k — коэффициент пропорциональности, то дно ассоциируется как 4 k:7k. Получено уравнение (4k + 7k) / 2 = 55. Видно, что k = 10. Это означает, что необходимые участки составляют 40 дм и 70 дм соответственно.

Поэтому средние линии треугольника и трапеции обладают одинаковыми свойствами. Темы очень похожи. Поэтому средняя линия трапеции равна половине суммы двух оснований.

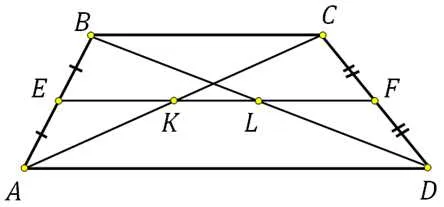
Дана таблица ABCD. Диагональ AC, пересекающая среднюю линию, образует точку K, а диагональ BD — точку L. Докажите, что отрезок KL равен половине разности оснований.

Трапеция — коротко о главном

Что такое трапеция:.

Трапеция — это четырехугольник с двумя параллельными сторонами (называемыми основаниями) и двумя непараллельными сторонами (боковыми сторонами).

Сумма углов двух сторон трапеции равна 180°.

\ \ displaystyle \ угол 1 + \ угол 2 = 180<>^ \ \ displaystyle \ угол 3+ \ угол 4 = 180°) и \ displaystyle \ угол 3+ \ угол 4 = 180°)<>^ \ displaystyle \ угол 1+ \ угол 2 = 180 ^ \ displaystyle \ угол 3+ \ угол 4 = 180)

Трапециевидная средняя линия:.

Средняя линия трапеции (Ј displaystyle MN \) — это часть, соединяющая середины сторон: Ј displaystyle AM = MB, Ј displaystyle \ \ CN = ND \).

Средняя линия параллельна основанию: 텞(텞 displaystyle MN \ параллель BC \ параллель AD \).

Длина средней линии трапеции равна половине суммы длин оснований: \(⌘ displaystyle MN = \ frac \).

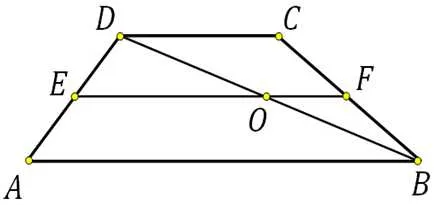
Диагонали трапеции:.

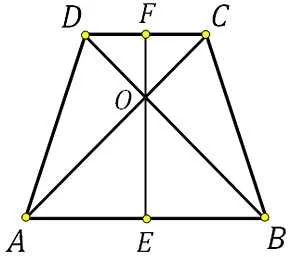
Диагонали каждой трапеции пересекаются в точке O.

Треугольники, образованные основанием и диагональными отрезками (⌘ (⌘ displaystyle BOC \) и ⌘ (⌘ displaystyle AOD \)), подобны по двум углам, причем подобие равно отношению оснований. \(⌘ displaystyle k = \ frac \)).

Треугольники, образованные сторонами и диагоналями трапеции, равны по площади: 섹 (섹 displaystyle _> = _> \)).

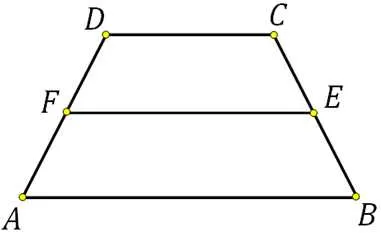
Равнобедренная трапеция (равнобедренная трапеция)

Равнобедренная трапеция — это трапеция, боковые стороны которой равны: ɛ(ɛ displaystyle AB = CD \).

Характеристики равнобедренных трапеций:.

Базовые углы равны: \ (\ displaystyle \ угол A = \ угол D, \ text< >\ዄ угол B = ዅ угол C), ዅ угол B = ዅ угол C), и

Сумма противоположных углов равна \(\ displaystyle 180<>^ \\\ circ \): \(\ displaystyle \ угол A + угол C = угол B + \ угол D = 180)<>^ \\\\ circ \).

Стороны и диагонали равнобедренной трапеции соединены в следующей пропорции: \ (\ displaystyle A ^> = B ^> = AD \ cdot BC + A ^> \).

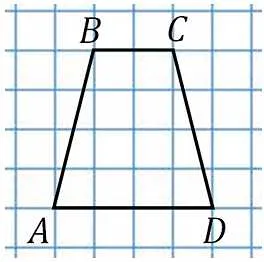
Если стол может быть зарегистрирован в круге…

Если трапецию можно вписать в окружность, то это равносторонний треугольник.

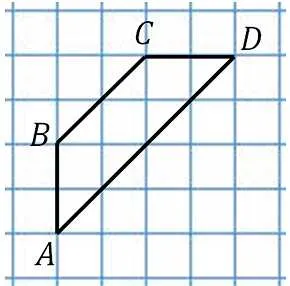
Площадь трапеции

Площадь трапеции равна половине суммы оснований высот: ߡ (ߡ displaystyle _> = \ frac \ cdot h \).

Примечание: учебники ЕГЭ по математике охватывают все темы по планетометрии и стереометрии (и алгебре).

Что такое трапеция?

Трапеция — это прямоугольник с двумя параллельными сторонами и двумя непараллельными сторонами.

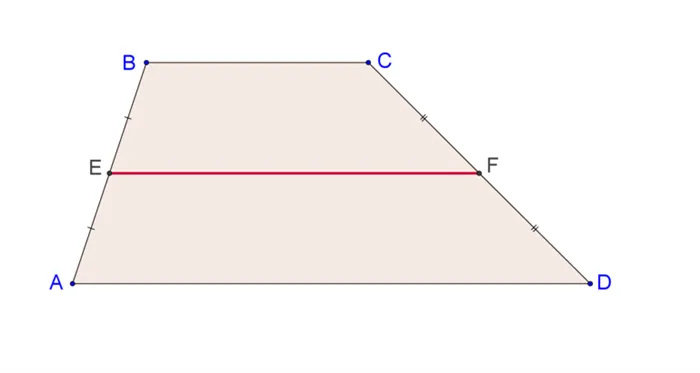
Параллельные стороны называются основаниями, а непараллельные — боковыми сторонами.

Трапеция (как и треугольник) может быть равнобедренным треугольником.

Если стороны равностороннего треугольника равны, он называется равнобедренным.

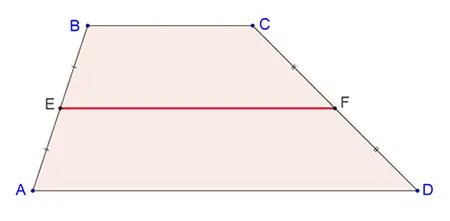
В связи с этим возникает вопрос: может ли трапеция иметь равные основания?

Нет, это не так. Во-вторых, это прямоугольник, а не стол. Это происходит потому, что стороны параллельны и равны (вспомните символ прямоугольника).

Свойства трапеции

Итак, что нам нужно знать о свойствах трапеции

Сумма углов с обеих сторон трапеции равна 180°. (Есть ᢙ Displaystyle \ угол 1 + \ угол 2 = 180<>^ \ \ displaystyle \ угол 3+ \ угол 4 = 180°) и \ displaystyle \ угол 3+ \ угол 4 = 180°)<>(^\ displaystyle circ \))

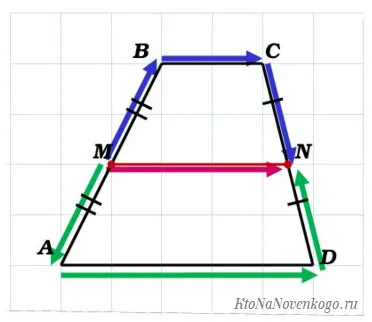
Ну, конечно, просто потому, что основания параллельны, а стороны вторичны.

Таким образом, мы видим, что углы внутри параллели ᢙ (ᢙ displaystyle \ ange 1 \) и ᢙ (ᢙ displaystyle \ angle 2 \) являются углами внутри параллели ᢙ (ᢙ displaystyle ad \) и ᢙ (ᢙ displaystyle bc \) и вторичными углами. (߁ displaystyle \).

Следовательно, ퟂ (ퟂ displaystyle \ угол 1 + угол 2 = 180)<>^ \\\\ circ \).

А точно такие же 섹 (섹 displaystyle \ ange 3 \) и 섹 (섹 displaystyle \ angle 4 \) являются одним углом внутри одной параллели 섹 (섹 displaystyle ad \) и 섹 (섹 displaystyle bc \), но вторичной теперь 섹 (섹 displaystyle bc \). displaystyle cd \).

Как видите, основную роль играет то, что она должна быть параллельна основанию. Давайте проанализируем еще несколько свойств трапеции.

Как и у каждого четырехугольника, у стола есть диагонали. Их два — см. рисунок:.

Обратите внимание, что высота, проходящая через диагональное пересечение, лежит на оси симметрии, а высота, проходящая через равнобедренный стол, делит стол на два равных прямоугольных стола. Это означает, что базы разделены по середине этой высоты.

Свойства равнобедренной трапеции:

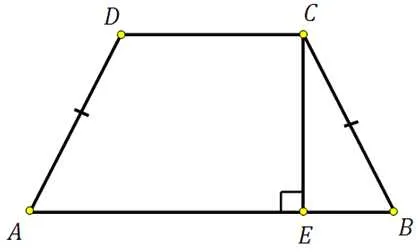
1. прямая, проходящая через среднюю точку основания, перпендикулярна основанию, поэтому симметрия изо-оболочки.

2. высота, приходящаяся на одну вершину большего основания трапеции изошеллы, делит ее на две части.

3. углы каждого основания изошара равны.

4. сумма противоположных углов изошильды равна 180°.

5. длины диагоналей равных трапеций равны.

6. циклы могут быть описаны вокруг таблицы изошелл.

7. если диагональ перпендикулярна таблице изошелей, то ее высота равна половине суммы оснований.

Формулы трапеции:

Пусть a — наибольшее основание трапеции, b — наименьшее основание трапеции, c — левая сторона трапеции, d — правая сторона трапеции, a и b — нижние углы основания трапеции, d₁ и г₂ — это диагонали трапеции, m — средняя линия трапеции, h — высота трапеции, c и d — углы между диагоналями трапеции, s — площадь трапеции, p — периметр трапеции.

Введите определение сторон трапеции:.

Через центральную линию и одно из оснований трапеции.

Через высоту и угол к нижнему основанию трапеции: p — высота и угол трапеции.

Через стороны и углы нижнего основания: через

Через высоту и угол к нижнему основанию трапеции: p — высота и угол трапеции.

Тип, определяющий центральную линию трапеции:.

Через длину основания трапеции: через длину основания трапеции.

Через площадь и высоту трапеции: через высоту трапеции

Тип, определяющий высоту трапеции: через

Через боковые и смежные углы и через углы, прилегающие к нижнему основанию трапеции: через углы, прилегающие к нижнему основанию трапеции

Через диагонали трапеции и углы между ними: через

Через диагонали трапеции и угол между ними и средней линией трапеции: через диагонали трапеции

Через площадь и длину основания трапеции:.

Через площадь и длину трапециевидной средней линии:.

Тип определения периметра трапеции:.

Через площадь и длину трапеции: тип определения площади трапеции: тип определения площади трапеции

Через основание и высоту трапеции: через основание и высоту трапеции

Через среднюю линию и высоту трапеции: через высоту трапеции

Через диагонали трапеции и углы между ними:.

Через каждую сторону трапеции:.

Через таблицу типа Geron:.

Как называется объемная трапеция?

Если стол представлен объемом, то такая форма похожа на граненую пирамиду.

В обычной усеченной пирамиде грани представляют собой таблицы с равными сторонами.

Примечание: © фотографии https: //www.pexels.com, https: //pixabay.com

Мировая экономика

Справочники

Востребованные технологии

• Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 946)
• Экономика Второй индустриализации России (103 201)
• Этилен (этен), получение, свойства, химические реакции (29 512)
• Программа искусственного интеллекта ЭЛИС (29 470)
• Метан, получение, свойства, химические реакции (26 572)
• Крахмал, свойства, получение и применение (26 037)
• Природный газ, свойства, химический состав, добыча и применение (25 164)
• Целлюлоза, свойства, получение и применение (24 311)
• Пропилен (пропен), получение, свойства, химические реакции (23 557)
• Прямоугольный треугольник, свойства, признаки и формулы (23 269)

Поиск технологий

О чём данный сайт?

Сайт посвящен научным разработкам автора в области экономики и научным идеям по осуществлению второй индустриализации России.

Включает:- Экономика второй индустриализации в России — Теории, методологии и инструменты инновационного развития — Реализация второй индустриализации в России — Организационные механизмы второй индустриализации в России — Справочник по инновационным технологиям.

Продукты и технологии не продаются. Производители и изобретатели! Вы должны связаться с ними напрямую!

Мы ведем переговоры с отечественными производителями и изобретателями инновационных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Применение второй российской индустриализации базируется на качественно новых научных основаниях (теориях, методологиях и инструментах), разработанных авторами.

Конечным результатом второй индустриализации России является рост благосостояния всех членов общества — среднего человека, предприятия и государства.

Вторая индустриализация России — это совокупность научных, технологических и других инновационных идей, планов и разработок, широко применимых к практике хозяйственной деятельности в краткосрочной перспективе (3-5 лет), ведущих к развитию качественно нового прогрессивного общества. в ближайшие 50-75 лет.

Первая страна, сделавшая это сложное открытие, Россия, стала лидером мирового сообщества и будет недосягаема для других стран еще многие века.