Если известны стороны треугольника и угол между ними, то площадь равностороннего треугольника вычисляется по типу «площадь треугольника через стороны и угол между ними».
Как найти площадь треугольника
Введение в геометрию начинается в 7 классе. Знания, полученные на этом этапе, помогут во взрослой жизни, если будущий человек захочет изучать точные науки. Изучая свойства фигур, необходимо научиться работать с треугольниками и вычислять их площади.
Прежде чем найти площадь треугольника, необходимо ознакомиться с его функцией.
Содержание:
Треугольник — это геометрическая фигура, состоящая из трех точек, расположенных на одной прямой, и трех отрезков, соединяющих эти точки. Отрезки называются сторонами, а точки — вершинами. Треугольники различаются по величине углов:.
Треугольники также различают по длине сторон.
- Равносторонние – три равных стороны.
- Равнобедренные – две равных стороны.
- Разносторонние ‒ три стороны с разной длиной.
Площадь каждой фигуры рассчитывается несколькими способами: через две или три стороны, тип зеолонга, основание и высоту. Как только вы ее поймете, геометрия сопровождает старшеклассников до окончания школы, а затем и университета, так что в дальнейшем она не вызывает трудностей.
Сегодня существуют онлайн-калькуляторы, которые могут производить расчеты, но прежде чем пользоваться такими помощниками, необходимо разобраться в символах и типах. Без базовых знаний невозможно правильно выполнить расчеты.

Как рассчитать площадь треугольника
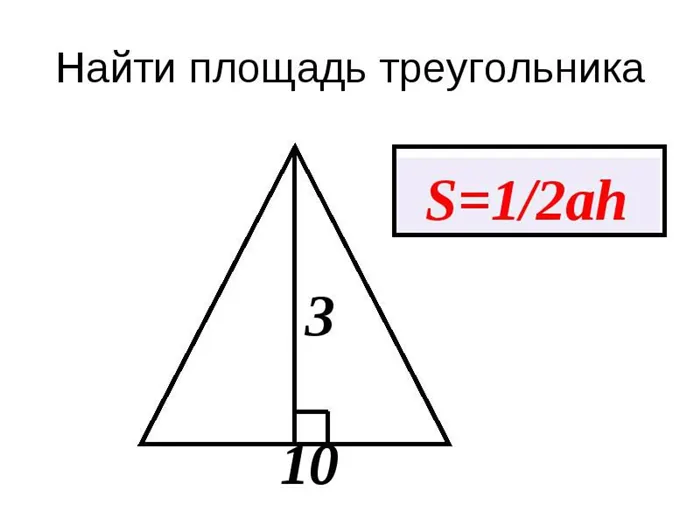
Одним из наиболее известных и распространенных методов расчета является метод базы и высоты. Для этого нужно перемножить основание и высоту между собой и разделить их на центры.
Здесь «a» — основание треугольника, а «H» — высота треугольника. Давайте на примере рассмотрим использование типа. Дана форма с основанием 6 см и высотой 4 см.
Сначала перемножьте два известных значения между собой, чтобы получить площадь нужной фигуры: s = 6*4 = 12 см.
Я не думаю, что когда-либо видел эту формулировку раньше. Следующий тип треугольной области применяется в очень редких случаях — когда известны два угла и стороны, с которыми эти углы соприкасаются.
Если треугольник прямоугольный
Другими словами, один из этих углов равен 90 градусам.
Катет необходимо умножить и разделить на два. Катетер имеет две меньшие стороны по сравнению с подчиненной. Подчиненная сторона является самой большой и всегда находится на противоположной стороне угла 90°.
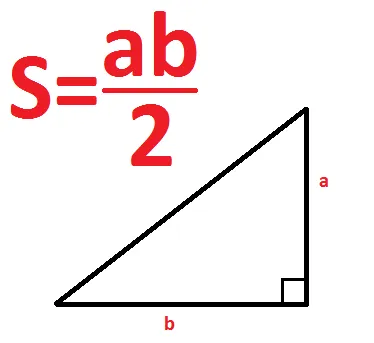
Если он равнобедренный
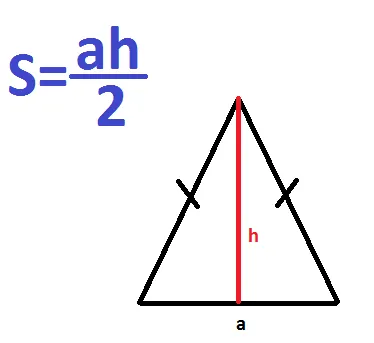
Поэтому у него равные стороны. В этом случае нужно начертить высоту основания (стороны, не равные «талии»), умножить основание на высоту и разделить оба на следствия.
Если он равносторонний
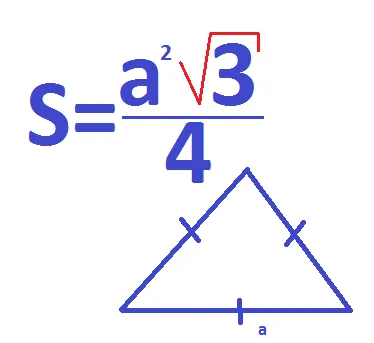
Другими словами, все три стороны равны. Ваша процедура выглядит следующим образом.
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Чтобы вычислить площадь треугольника изошеллы, нужно использовать классический тип: с = ах. Чтобы определить высоту, нужно обратиться к теореме Пифагора или вычислить тип Герона. Это объясняется ниже.
Площадь треугольника
Теперь вам не придется тратить время на долгие вычисления, чтобы найти площадь треугольника. Узнав метод вычисления площади треугольника, вы сможете легко выполнить его самостоятельно. Действительно, всегда лучше знать вид площади треугольника. Треугольники бывают разные, вы это знаете, но как найти площадь треугольника, если вы почти ничего не знаете о треугольниках? А чтобы найти площадь, нужно знать размеры треугольника. Давайте разберемся в сути вопроса. Это не так просто, как кажется на первый взгляд. Поэтому задача на нахождение площади треугольника, вероятно, существует и в GCSE, и в математике.
Треугольник — это геометрическая фигура. По определению, это трехсторонний многоугольник. Следовательно, треугольник должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы вычислить площадь треугольника, сначала нужно знать размеры его основания и высоту. Основание треугольника представляет собой одну из его сторон. С другой стороны, высота представляет собой каждую из трех линий, проходящих через одну из вершин треугольника и перпендикулярных противоположной стороне допустимой вершины (т.е. перпендикулярных основанию).
Во-первых, запомните, что треугольник имеет три стороны и три угла. Это означает, что требуется три вершины. Треугольник с вершинами A, B и C можно представить следующим образом: ΔABC. Треугольники бывают разных типов. Их можно классифицировать двумя различными способами: либо по характеру сторон, либо по угловым характеристикам.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Распознать неправильный треугольник с тремя сторонами разной длины. Эти треугольники могут быть построены только под тремя различными углами. Более того, один из них может быть прямым углом (или углом 90°). Обычно название «произвольный треугольник» используется для неправильных треугольников.
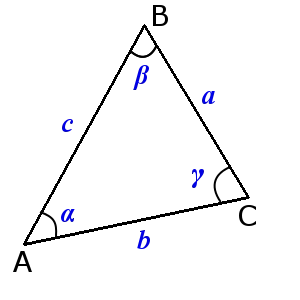
Равнобедренный треугольник
Треугольник называется равнобедренным, если у него две стороны равной длины при основании и два равных угла. Равнобедренные треугольники также можно определить по тому, что их высоты представляют собой ось симметрии, медиану и биссектрису.
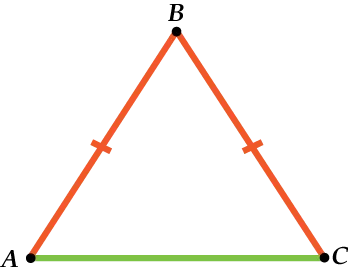
Прямоугольный треугольник
Правильные треугольники обязательно прямоугольные. Это означает, что сумма двух других углов должна быть равна 90°. Прямоугольные треугольники также имеют косые стороны.
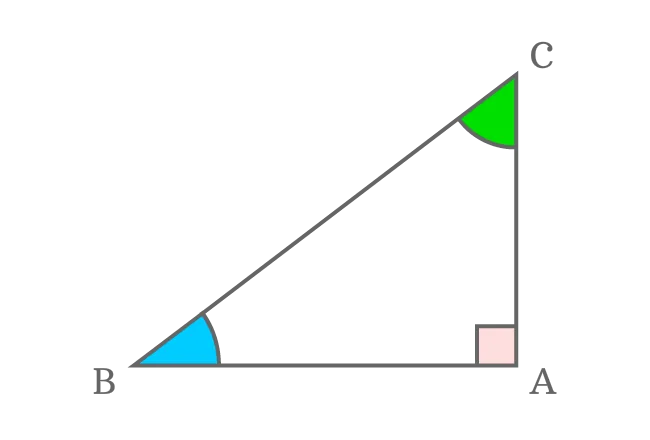
Это противоположный прямому угол с вершиной. Прямоугольный треугольник может стать неправильным треугольником (или любым треугольником), если три его стороны имеют разную длину.
Он также может быть равнобедренным треугольником, если есть два одинаковых катетера.
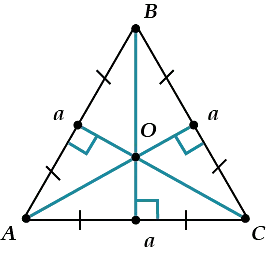
Равносторонний треугольник
Если у треугольника три стороны одинаковой длины, он называется равносторонним. Поэтому все его углы также равны, каждый из них равен 60°. В равностороннем треугольнике каждая высота также служит медианой и биссектрисой.
Площадь треугольника
Площадь разностороннего треугольника
Вычислите площадь треугольника, который не является равным — все его стороны разные и все углы разные.

Если известны стороны треугольника и угол между ними, то площадь равностороннего треугольника вычисляется по типу «площадь треугольника через стороны и угол между ними».
Если высота и основание треугольника известны, то используется формула для площади и высоты треугольника через основание: «площадь треугольника через основание и угол между ними».
Формула Герона определения площади треугольника
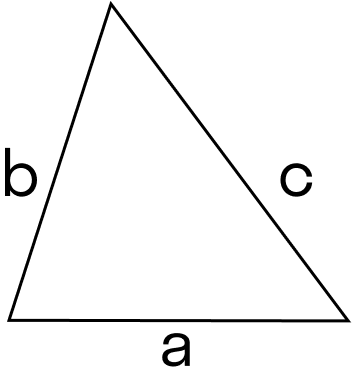
Если известны стороны треугольника, площадь можно найти по формуле Герона.
 Площадь равнобедренного треугольника
Площадь равнобедренного треугольника
Если известны стороны и основание равнобедренного треугольника, то можно найти площадь треугольника с основанием и сторонами.
Формула для площади треугольника относительно основания, сторон и угла между ними применима и к равнобедренным треугольникам: площадь треугольника с основанием, сторонами и углом между ними можно найти и для равнобедренных треугольников.
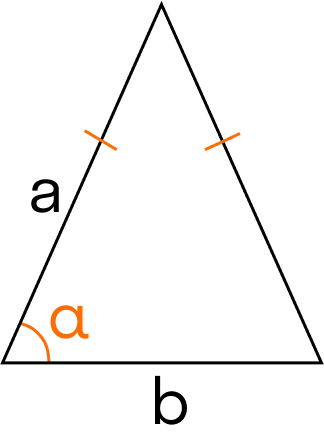
Вы также можете найти площади равнобедренных треугольников и углы между ними.
Площадь равнобедренного треугольника через основание и угол между сторонами:.
Площадь прямоугольного треугольника
Формула для площади прямоугольного треугольника имеет вид Формула площади правильного треугольника через перпендикуляр и смежные углы:.
Площадь правильного треугольника с конечными радиусами и косыми сторонами
Площадь прямоугольного треугольника (если он вписан в окружность):.
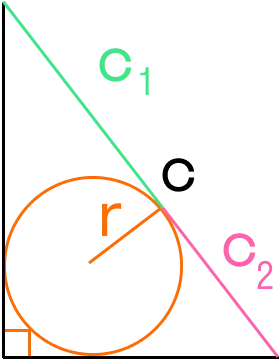
Площадь равностороннего треугольника
Площадь правильного треугольника можно найти через радиус окружности.

Учитывая радиус круга, площадь равностороннего треугольника можно найти по следующей формуле: .
Такая фигура также называется правильным треугольником. Для вычислений используется классическая формула для вычисления и замены высоты равнобедренного треугольника.
Площадь треугольника через радиус вписанной окружности и 3 стороны
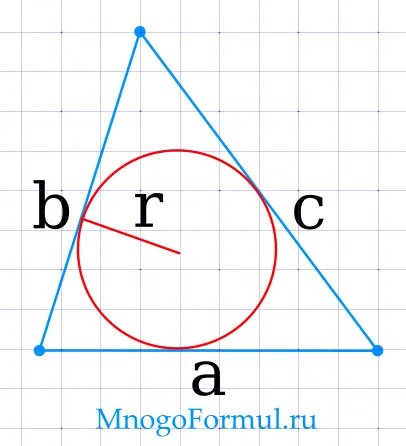
Формула для нахождения площади треугольника через конечную окружность и стороны:.
>, где a, b и c — стороны треугольника, а r — радиус выгравированного круга.
Формулу можно переписать по-другому, если > считать полусферой треугольника. В этом случае уравнение принимает вид S =, где p — полусфера треугольника.
Правильные треугольники обязательно прямоугольные. Это означает, что сумма двух других углов должна быть равна 90°. Прямоугольные треугольники также имеют косые стороны.
Как найти площадь треугольника: инструкция
В зависимости от исходных данных существует несколько способов вычисления площади треугольника. Давайте рассмотрим несколько основных формул для расчета этого значения.

Как найти площадь треугольника по высоте и основанию
Высота — это линия, проведенная под прямым углом от вершины треугольника к противоположной стороне.
Чтобы вычислить площадь, необходимо знать высоту и длину стороны, на которой она нарисована. Умножьте высоту на длину стороны и разделите результат пополам. Формула становится
где S — площадь, h — высота и α — сторона треугольника.
Как найти площадь треугольника по трём сторонам
Этот метод также известен как формула Герона. Чтобы воспользоваться им, необходимо знать длину каждой стороны треугольника и вычислить полуокружность.
Полупериметр обозначается p. Это равно половине суммы длин всех сторон.
Где a, b и c — стороны треугольника.
Затем вычислите произведение полуокружности и разницы между каждой стороной, умножьте полученное число на полуокружность и найдите квадратный корень из полученного результата. Это показано в виде уравнения.
Катет необходимо умножить и разделить на два. Катетер имеет две меньшие стороны по сравнению с подчиненной. Подчиненная сторона является самой большой и всегда находится на противоположной стороне угла 90°.
Ⅱ. Через все стороны и периметр
p — половина окружности и рассчитывается по формуле \ p = \ frac \), где a, b и c — стороны треугольника.
Эту формулу следует использовать, когда известны все три стороны треугольника. Знание трех сторон треугольника позволяет найти периметр, а затем и площадь конкретного треугольника.
Этот тип региона также называют типом Герона.
Ⅲ. Через две стороны и угол между ними
\ S = \ frac a \ cdot b \cdot\sinβ\
α и β — углы β, а sinβ — ребро, являющееся синусом угла β.
Эта формула применяется, когда известен один из углов и две стороны, образующие этот угол. В некоторых задачах площадь треугольника можно найти только по этой формуле.
Ⅵ. Через сторону и два прилежащих к ней угла
α — сторона треугольника, sinα — синус угла α и sinβ — синус угла β.
Я не думаю, что когда-либо видел эту формулировку раньше. Следующий тип треугольной области применяется в очень редких случаях — когда известны два угла и стороны, с которыми эти углы соприкасаются.
В равнобедренном треугольнике все стороны имеют одинаковую длину, поэтому для вычисления нужно знать только одну сторону. Умножьте квадрат стороны на квадратный корень из 3 и разделите на 4.
Как найти площадь треугольника
Существуют различные типы углов, которые позволяют вычислить площадь фигуры с тремя углами. Поэтому вы можете выбрать тот, который облегчает эту задачу. Прежде чем приступить к составлению уравнения, необходимо ознакомиться с несколькими понятиями.
S — площадь фигуры, и
a, b и c — стороны, и
h — значение высоты многоугольника, и
R — значение радиуса окружности, описанной вокруг диаграммы.
Это наиболее распространенные символы, встречающиеся в формулах, используемых для вычисления площади треугольника. Рекомендуется запомнить основы, так как они пригодятся не только при выполнении уроков с ребенком, но и в повседневной жизни. Простейшее уравнение:.
Прямоугольный треугольник и расчет его площади
Такой треугольник — это треугольник, углы которого правильные, то есть равны 90 градусам. Одинаковые углы (прямые углы) многоугольника образуются двумя вертикальными отрезками. Обратите внимание, что в треугольнике может быть только один такой (прямоугольный) угол, так как в обоих случаях сумма равна 180 градусам. Таким образом, сумма двух других углов равна 90 градусам. Это основные элементы геометрии, которые знает каждый школьник. Итак, когда перед вами именно такой правильный треугольник, как найти его площадь?
- Проще всего это можно сделать, воспользовавшись формулой, которая уже известна: S=a*b/2
- Есть и другие формулы, но для таких вычислений, вам понадобиться таблица синусов (sin), косинусов (cos) и тангенсов (tg):
- S=a²/2tgα;
- S=b²/2tgβ;
- S=a²*tgβ/2;
- S=b²*tgα/2;
- S=c²*sunα*cosα/2;
- S=c²*sinβ*cosβ/2;
- S=c²*sinα*sinβ/2.
Равнобедренный треугольник
Если вам нужно вычислить площадь контурного треугольника, проще всего это сделать с помощью классической формулы: .
Помните, что контурный треугольник — это треугольник, две из трех сторон которого равны друг другу. Третья сторона — это основание. Однако не путайте это с изоклеточными треугольниками. Такие (равнобедренные или прямоугольные) треугольники — это треугольники с равными (одинаковыми) длинами сторон. Для изоклеточных треугольников также можно использовать следующую формулу для нахождения площади
S = (a * c / 2)* cos(y / 2) = (a * c / 2)* sin(beta / 2), где
S = a²*sin (y / 2)* cos (y / 2) = a²* sin (α/ 2)* cos (α/ 2), и
Угол α — это угол между одной из сторон фигуры и основанием, а угол y — угол между (равными) сторонами.
Конечно, использование таких формул требует свободного использования таблиц синусов, косинусов и тангенсов, которые не являются удобными и общедоступными.








