В результате у нас получился прямоугольник, длины обеих сторон которого известны (высота прямоугольника теперь является одной из его сторон). Как известно, площадь прямоугольника равна произведению его сторон.
Как найти площадь параллелограмма abcd: формула через стороны, диагонали
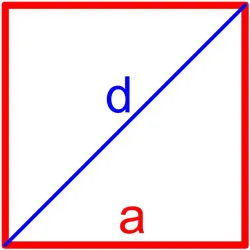
Каждая диагональ прямоугольника делит его на два равносторонних треугольника, поэтому используйте эти свойства для экспорта типа в прямоугольные диагонали.
В каждом треугольнике противоположные углы и стороны пропорциональны друг другу. Для прямоугольника это означает, что наибольшая диагональ находится напротив тупого угла, а наименьшая диагональ — напротив острого угла. Учитывая, что стороны диагоналей получившегося треугольника одинаковы, они являются сторонами прямоугольника, а измерение градуса угла на этих сторонах определяет длину диагоналей, вычисленную по формуле. Другими словами, заменяя значение острого угла прямоугольника диагонального типа, калькулятор вычисляет длину малой диагонали; заменяя стоимость тупого угла — большой диагонали.
Для перехода от одного угла к другому используется разность 180 градусов и заданного угла, что позволяет калькулятору вычислять обе диагонали одновременно.
Чтобы привести формулу прямоугольной диагонали, теорема косинусов используется в треугольниках, где диагонали образуют стороны и фигуры. В каждом таком треугольнике диагональ находится на противоположной стороне угла прямоугольника, поэтому ее площадь равна сумме площадей двух других сторон треугольника (в данном случае сторон прямоугольника). Произведение одинаковых сторон на косинус этого угла. Чтобы найти длину диагонали прямоугольника, калькулятор вычисляет квадратный корень из этого уравнения.
Формула вычисления площади
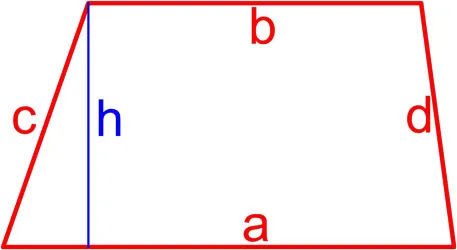
1. с боков и высоты:.
Площадь прямоугольника равна произведению его сторон и запланированной в нем высоты.

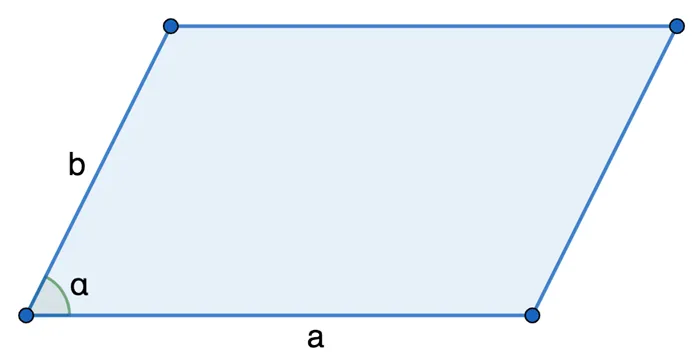
2. с боков и угол между ними:.
Площадь параллелограмма умножается на длину обеих сторон и полутон между ними.
s = a * b * sin a
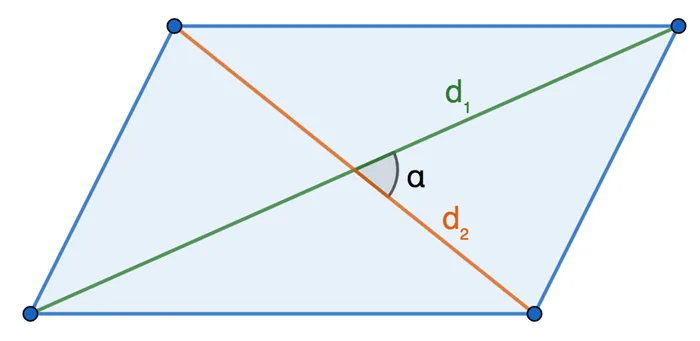
3. от двух диагоналей и угла между ними: угол
Площадь прямоугольника равна одной второй длины диагонали половины его углов.
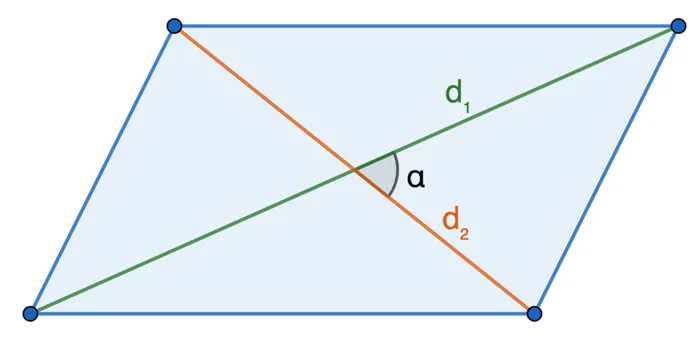
S = 1/2 * d1 *d2 *син а.
Площадь параллелограмма через диагонали
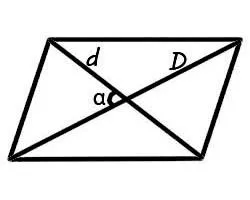
Тип площади, проходящей через диагонали прямоугольника, позволяет быстро находить цены. Для расчета требуется значение угла между диагоналями.
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75
Знание пресса о прямоугольной области через диагонали решает ряд интересных задач. Давайте посмотрим на один из них.
Проблема:.Дан параллелограмм с площадью 92 кв. см. Точка F расположена на середине его стороны ВС. Давайте найдем площадь трапеции ADFB, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям. Приступаем к решению: По нашим условиям ah =92, а соответственно, площадь нашей трапеции будет равняться
В результате у нас получился прямоугольник, длины обеих сторон которого известны (высота прямоугольника теперь является одной из его сторон). Как известно, площадь прямоугольника равна произведению его сторон.
Через основание и высоту
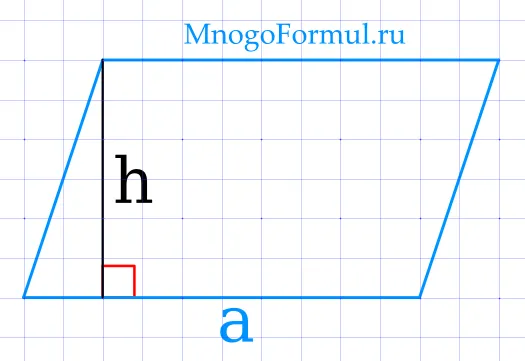
Нахождение площади прямоугольника через его основание и высоту Тип:.
Где a — основание прямоугольника, а h — его высота, спроектированная на основание.
Через стороны и угол между ними
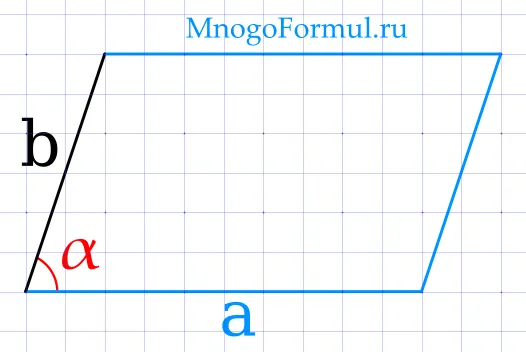
Человек находит площадь прямоугольника по его стороне и углу между ними:.
) >, где a и b — стороны прямоугольника, а a — угол между сторонами.
Через диагонали и угол между ними
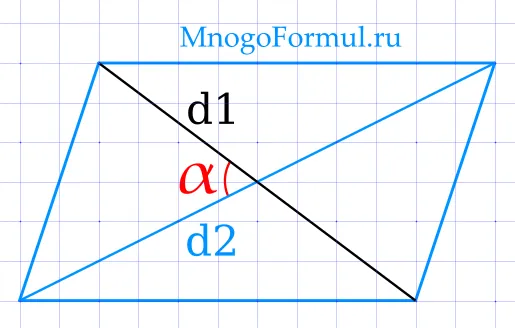
Человек, который находит площадь прямоугольника через диагонали и угол между ними:)
\ cdot d1 \ cdot d2 \ cdot \ sin ()>, где d1 и d2 — диагонали прямоугольника, а a — угол между ними.
Здравствуйте, читатели блога KtoNaNovenkogo.ru. Эта статья посвящена другой математической теме. В ней объясняется, как правильно вычислить площадь прямоугольника. Эта тема подробно изучается только в 8 классе. Но дело в том, что все не так просто.
Нахождение площади параллелограмма: формула и примеры
Прямоугольник — это геометрическая фигура, четырехугольник с равными и параллельными противоположными сторонами.
По длине стороны и высоте
Площадь прямоугольника равна произведению его сторон и запланированной в нем высоты.
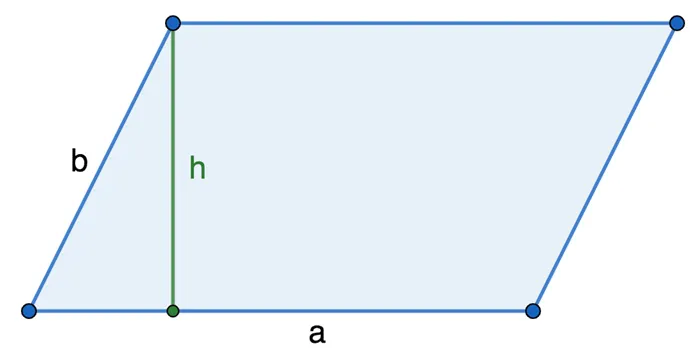
По двум сторонам и углу между ними
Площадь параллелограмма умножается на длину обеих сторон и полутон между ними.
S=a⋅b⋅sinα
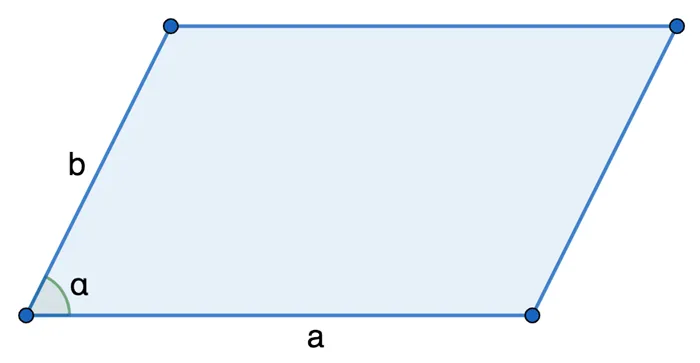
По двум диагоналям и углу между ними
Площадь прямоугольника равна одной второй длины диагонали половины его углов.
Примеры задач
Задача 1Найдите площадь прямоугольника, если его длина равна 7 см, а высота — 4 см.
Решение: используем первое уравнение, содержащее известные из условия задачи значения: s = 4 см * 7 см = 28 см2.
Задача 2Найдите площадь прямоугольника, если его стороны равны 6 см и 8 см, а угол между ними равен 30°.
Решение: примените вторую формулу выше: s = 6 см * 8 см * sin30° = 24 см2.
Задача 3: Найдите площадь прямоугольника, диагонали которого равны 4 см и 6 см. Угол между ними равен 90°.
Решение: используйте формулу, в которой фигурируют диагонали: s = 1/2 * 4 см * 6 см *sin90°=12 см2.
Помните из школы, что можно вычислить вписанную окружность и ребро, проходящее через окружность. Это будет 2* на сторону для каждого радиуса круга. Также можно найти радиус и угол между сторонами, но эти типы редко используются, но могут быть полезны для некоторых задач.
Как найти площадь параллелограмма
WikiHow работает как вики. Это означает, что многие наши статьи написаны более чем одним автором. Эта статья была отредактирована и улучшена девятью людьми, включая анонимных авторов.
Эту статью просмотрели 8254 человека.
Прямоугольник определяется как простой четырехугольник с двумя парами параллельных сторон. При создании геометрических фигур вам может понадобиться найти площадь прямоугольника. Вот несколько советов, которые помогут вам сделать это правильно.
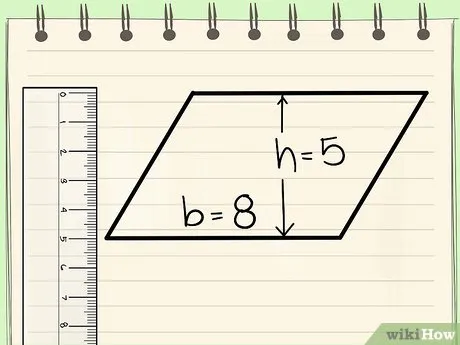
Найдите высоту прямоугольника. Высота прямоугольника — это вертикальная линия, проведенная из любой точки верхней стороны прямоугольника в нижнюю.
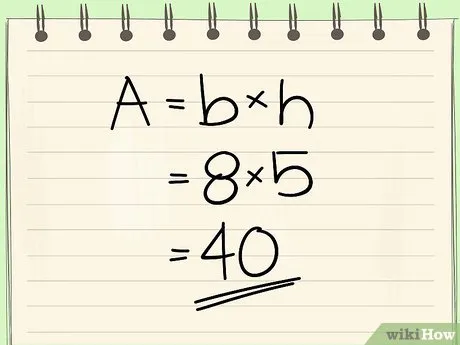
Дополнительные статьи
Об этой статье
WikiHow основан на Вики. Это означает, что многие наши статьи написаны более чем одним автором. Эта статья была отредактирована и улучшена 9 анонимными авторами. Эту статью просмотрели 8254 человека.
Cookies помогают нам сделать WikiHow лучше. Продолжая пользоваться нашим сайтом, вы соглашаетесь с нашей политикой использования файлов cookie.
Каждая диагональ прямоугольника делит его на два равносторонних треугольника, поэтому используйте эти свойства для экспорта типа в прямоугольные диагонали.
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, читатели блога KtoNaNovenkogo.ru. Эта статья посвящена другой математической теме. В ней объясняется, как правильно вычислить площадь прямоугольника. Эта тема подробно изучается только в 8 классе. Но дело в том, что все не так просто.

Но сначала напомню, что фигура называется прямоугольником.
Прямоугольник — это тип четырехугольника, противоположные стороны которого параллельны друг другу.
Классический прямоугольник выглядит следующим образом
Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем знаменитом труде «Элементы». Он также описал два особых случая прямоугольника в том виде, в котором он известен нам сегодня.
Это прямоугольники, противоположные стороны которых не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, все стороны которого также равны друг другу, за исключением противоположных параллелей.
Наконец, стоит вспомнить, что означает термин «территория».
Площадь геометрической фигуры — это размер внутренних плоскостей сторон фигуры.
Далее давайте объединим эти два понятия, чтобы проиллюстрировать, как вычислить площадь прямоугольника.
Формулы для расчета площади параллелограмма
Существует три основные формулы для вычисления площади прямоугольника: — площадь прямоугольника — площадь боковых плоскостей прямоугольника — и — площадь самого прямоугольника.
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Далее каждый из них будет рассмотрен более подробно.
Как найти площадь параллелограмма, если известны сторона и высота
В качестве примера возьмем этот прямоугольник.
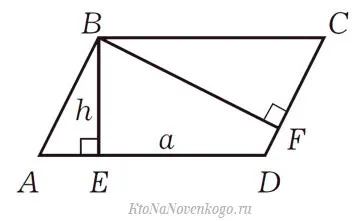
Он имеет две высоты, BE и BF. Обратите внимание, что высота — это отрезок, опускающийся под прямым углом от вершины к противоположной стороне.
В этом случае вычислить площадь очень просто. Просто умножьте длину на высоту и длину стороны, на которой она нарисована.
То же самое верно, если вы знаете длину стороны DC и высоту BF. Затем их нужно перемножить, чтобы вычислить площадь.
Кстати, у этого человека есть очень интересные доказательства. Поскольку противоположные стороны прямоугольника параллельны и равны, мы можем взять треугольник ABE и переместить его на сторону CD. Вот как это выглядит:.
В результате у нас получился прямоугольник, длины обеих сторон которого известны (высота прямоугольника теперь является одной из его сторон). Как известно, площадь прямоугольника равна произведению его сторон.
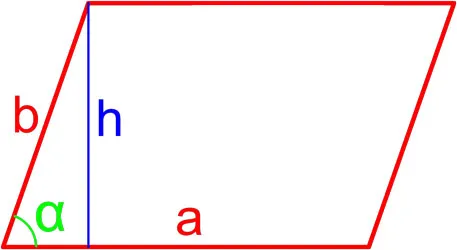
Формула площади параллелограмма, если известны стороны и угол
Площадь прямоугольника можно вычислить, если известны длины двух его сторон и величина острого угла между ними.
Фактически, этот метод является производным от предыдущего. Он просто использует исходные данные для расчета высоты прямоугольника, а затем использует их для расчета площади.
Согласно тригонометрии, синус острого угла прямоугольника равен отношению перпендикуляра к диагонали. В данном примере возвышение — это катетер, а косая сторона — это сторона «а». И выясняется, что:.
Поэтому для расчета значения высоты нам необходимы: a) площадь катета, b) площадь катета, c) площадь катета, d) площадь катета, e) площадь катета.
Окончательная формула для вычисления площади становится следующей
Трапеция — это прямоугольник с двумя параллельными (a, b) сторонами (основания) и двумя другими непараллельными (c, d) сторонами (боковые стороны).
Площадь параллелограмма
Площадь прямоугольника можно вычислить тремя способами. При первом способе нужно знать длину стороны и высоту, приходящуюся на эту сторону; при втором способе нужно знать две стороны и угол между ними; при третьем способе нужно знать длину и угол диагоналей. пересечения этих диагоналей.
Для первого метода достаточно знать длину стороны (a) и высоту, приходящуюся на сторону (h). Мужчина:.
Пример: Например сторона a равна 8см, высота h равна 4см, площадь параллелограмма равна
По диагоналям и углу пересечения
При третьем способе необходимо знать длины диагоналей AC и BD и угол ∠AOB. Мужчина.
Пример: например, диагональ AC равна 7 см, диагональ BD равна 5 см, угол ∠AOB равен 60° (sin(60°) равен примерно 0,87), а площадь прямоугольника = 15,225″/> см 2 .
Кстати, у этого человека есть очень интересные доказательства. Поскольку противоположные стороны прямоугольника параллельны и равны, мы можем взять треугольник ABE и переместить его на сторону CD. Вот как это выглядит:.
Формулы площади дельтоида
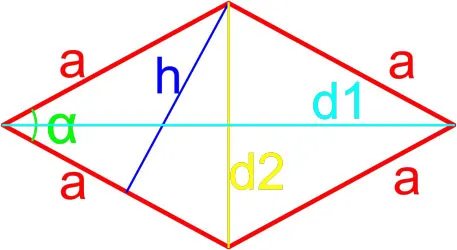
Дельтоид — это выпуклый четырехугольник, состоящий из двух разных равнобедренных треугольников с общим основанием, вершина которого находится на противоположной стороне этого основания.
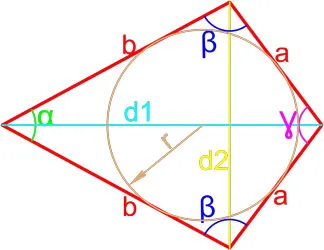
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтовидной мышцы равна произведению длин сторон, неравных половине ее углов.
Где s — площадь дельтоида, a и b — длины неравных сторон дельтоида, b — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтовидной мышцы равна половине суммы произведения каждой пары сторон, равной половине угла.
s = a 2 sin c + b 2 sin a 2, где
где s — площадь дельтоида, a и b — длины сторон дельтоида, a — угол между равными сторонами b и c — угол между равными сторонами a.
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтовидной мышцы равна произведению суммы неравных радиусов сторон в клетке.
Где S — площадь дельтовидной мышцы, a и b — длины неравных сторон дельтовидной мышцы, r — радиус в клетке.
Формула площади дельтоида по двум диагоналям
Площадь дельтовидной мышцы равна половине произведения двух диагоналей.
Где S — дельтовидная поверхность, D1, D2 — косой угол дельтовидной кости.
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь любого выпуклого четырехугольника равна углу, равному половине произведения его диагоналей.
Где s — площадь четырехугольника, d1 и d2 — диагонали четырехугольника, а c — один из четырех углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
S = P -A P -B P -C P -D -A -B -C -D -COS2θ, где
где S — площадь четырехугольника, a, b, c, d — длины сторон четырехугольника, p = α +β +Δ2 — противолежащий угол четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если четырехугольник может быть описан четырехугольником, то его площадь равна
где s — площадь четырехугольника, a, b, c, d — стороны четырехугольника, p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если четырехугольник может быть зарегистрирован как круг, то его площадь равна
где s — площадь четырехугольника, r — радиус зарегистрированной окружности, а p = a + b + c + d 2 — полупиновый метр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
Если четырехугольник может быть описан четырехугольником, то его площадь равна
где s — площадь четырехугольника, а a, b, c и d — длины сторон четырехугольника.
Формулы площади круга
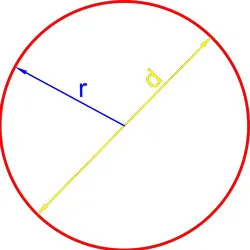
Формула площади круга через радиус
Площадь круга равна произведению квадратов радиуса на число P.
где S — площадь круга, а R — радиус круга.
Формула площади круга через диаметр
Площадь круга равна одной четверти произведения квадратов диаметра на число P.
Где S — площадь круга, а D — диаметр круга.








