Решение: стороны a = 8, b = 9 и c = 11. По типу Герона площадь треугольника можно определить по следующему виду: a = √(sx(sa)x(sb)x(sc)). Сначала нужно определить s — полуокружность треугольника: s = 1⁄2x(a+b+c) = 1⁄2x(8+9+11) = 14.
Формулы площадей всех фигур в геометрии — примеры вычислений
Это мера объема пространства, содержащегося в плоской форме. В общем случае, поверхность — это сумма всех площадей геометрической формы, которые покрывают поверхность объекта. Вычисление поверхности тела часто необходимо в повседневной жизни. Чтобы узнать количество краски, которую необходимо приобрести для покрытия стен и шифера для ремонта крыши дома.
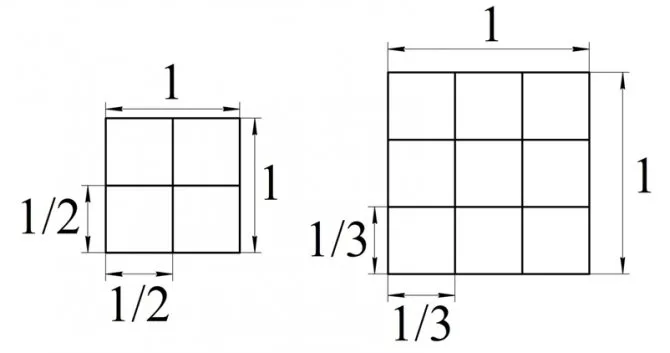
Люди давно научились использовать метод сетки для определения областей плоских геометрических форм. Он состоит из покрытия простой квадратной масштабируемой сетки. 1×1 см, измеряемая форма. Измерив количество квадратов в сетке на диаграмме, легко вычислить площадь квадратов. В этом случае каждая ячейка имеет ширину 1 см и высоту 1 см; площадь этой квадратной ячейки равна квадратным сантиметрам.
Подсчет квадратов фигуры с помощью сетки — это очень простой способ определения площади, но он не может быть применен для определения сложных фигур. Площадь таких сложных объектов может быть вычислена с помощью простых математических типов. Самые простые и часто используемые в жизни вычисления — это площади квадратов и прямоугольников, где нужно знать, как вычислить площадь в измерениях.
Во многих случаях расчеты могут быть более сложными. Например, типичный план помещения не может состоять из простых прямоугольников или квадратов. В этом случае сложную измеряемую поверхность необходимо разделить на различные простые геометрические фигуры, прежде чем можно будет рассчитать общую площадь.
Треугольник
Тип нахождения площади треугольника представлен несколькими способами.
1) Площадь треугольника вычисляется по основанию A и высоте h. Основание — это сторона геометрии с уменьшающейся высотой. Тогда площадь треугольника равна
2) Площадь прямоугольного треугольника вычисляется точно так же, если подчиненная сторона считается основанием. Если за основание принять подножие, то площадь прямоугольного треугольника равна половине произведения вертикали.
На этом тип вычисления площади треугольника не заканчивается. Другая формула включает стороны A, B и функцию угла c, заключенного между A и B. Значения синуса взяты из таблицы. Их также можно найти с помощью калькулятора. Далее, площадь треугольника:.
Это равенство также показывает, что площадь прямоугольного треугольника определяется длинами его вершин. Поскольку угол C — прямой, площадь прямоугольного треугольника вычисляется без умножения на функцию синуса.
Рекомендуется: тип уменьшения треугольника. Подробное описание.
3) Рассмотрим частный случай прямоугольного треугольника, сторона A которого известна по условиям или длина которой находится в решении. Больше о геометрической форме задачи ничего не известно. Как же найти площадь при таком условии? В данном случае формула применяется к площади прямоугольного треугольника.
Простой расчет прямоугольника

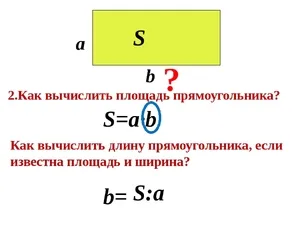
Внимательно посмотрите на свое окружение, и вы увидите множество примеров прямоугольников. По определению, прямоугольник — это четырехугольник, углы которого образуют угол 90°. Вычисление площади поверхности прямоугольного тела — это простая математическая практика, которая чаще всего используется в повседневной жизни, чем человеком. Почему важно знать тип территории? Многие предметы и обстановка вокруг людей имеют прямоугольную форму — дома, стены, полы, крыши и т.д. И очень часто для строительства или ремонта необходимо знать их площадь.
Если прямоугольник имеет ширину b и h, то площадь s можно найти, умножив ширину на длину. Следовательно, s = bxh.
Пример. Как вычислить площадь прямоугольника, если известны его стороны и ширинаДлина равна 4 см, а ширина — 3 см. Тогда s = 4×3 = 12.
Квадрат — это разновидность прямоугольника с равными углами и сторонами.
Пример. Если сторона квадрата равна 3 см, то можно найти s квадратов. Таким образом, мы имеем S = 3×3 = 9.
Задание. Численно площадь квадрата равна его периметру (площадь измеряется в см2, а периметр — в см). Вычислите его площадь.
Что такое площадь и как ее найти?
Эта площадь характерна для замкнутой геометрической фигуры (например, круг, квадрат, треугольник и т.д.), указывая на ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Он обозначается буквой s (квадрат).
1. наиболее известный вид площади треугольника, основанный на сторонах и высоте:.
s = a — h
где a — длина основания, а h — высота треугольника, проведенная к основанию.
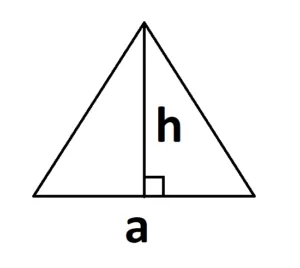
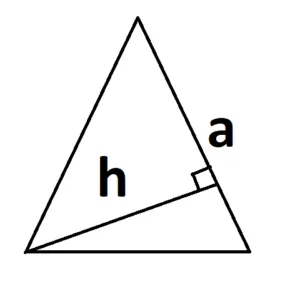
И основание не обязательно должно быть внизу. И это нормально.
Если треугольник тупой, то высота опускается за основанием.
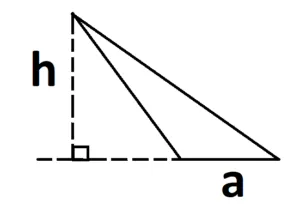
Если треугольник прямоугольный, то основание и высота являются его катетами.
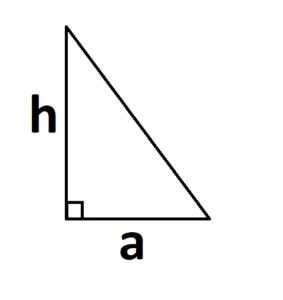
2. другая формула. Это тоже не полезно, но почему-то всегда забывается.
s = a -b -sina
где A и B — две стороны треугольника, поэтому Sina — синус угла между этими сторонами.
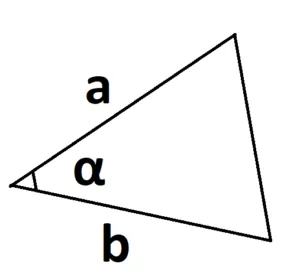
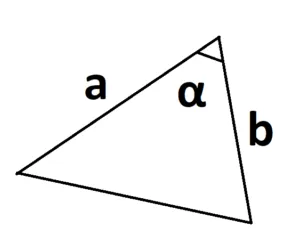
Основным условием является то, что угол берется между двумя известными сторонами.
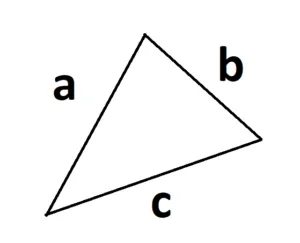
3. трехсторонний тип (тип Geron):.
S =
где a, b и c — стороны треугольника, а p — полупинеметр. p = (a + b + c)/2.
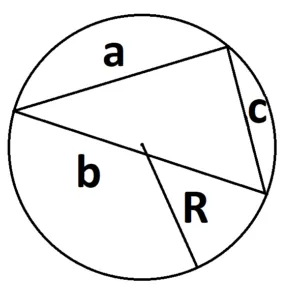
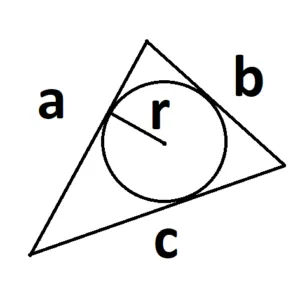
4. введите площадь треугольника через радиус области.
S =
где a, b и c — стороны треугольника, а r — радиус окружности.
5. введите площадь треугольника через радиус области:.
S = P — R
где p — полусветимость треугольника, а r — радиус в ячейке.
(1) Поскольку квадрат — это прямоугольник, у которого все стороны равны, к нему применим тот же тип.
s = a — a = a 2
(2) Площадь квадрата также можно найти по его диагоналям.
S = D 2
Как найти площадь круга?
1.Площадь круга можно найти через его радиус
S = piR2
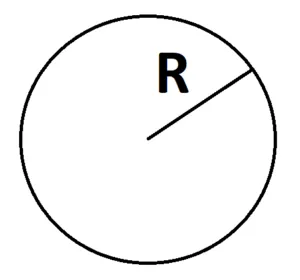
2.Площадь круга можно найти по его диаметру.
S =πD2/4
Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.
Площадь фигуры
Площадь плоской фигуры — это простейшая числовая характеристика фигуры, принадлежащей к одному уровню в целом. В простейшем случае, если фигуру можно разделить на конечное число единичных квадратов, площадь равна числу квадратов.
Формальное введение в понятия площади и объема можно найти в книге Jordaan Measure. Здесь в комментариях приводится только одна идея определения.
Поскольку площадь является функцией фактических значений, определенных в определенной категории евклидовых уровней, следует, что
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1; фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определенные классы должны быть замкнуты в терминах пересечений и сумм, а также в терминах движения плоскости, и должны включать все многоугольники. Из этих аксиом вытекает монотонность регионов.
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура квадрируемой, если для любого существует пара многоугольников , такие что , где обозначает площадь
Связанные определения
На самом деле, существует довольно неестественный и неоднозначный способ определения области всех ограниченных подмножеств уровня. Множество всех ограниченных подмножеств плоскости имеет различные функции площади, то есть функции неравенства, которые удовлетворяют вышеуказанным аксиомам, а множество квадратных фигур является самым большим множеством фигур, для которых функция площади определена однозначно.
То же самое можно сказать о длине прямой линии, но не об объеме евклидова пространства или площади единичной сферы в евклидовом пространстве (см. парадокс Банаха-Тарского и Хаусдорфа, соответственно).
Площади некоторых фигур
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Площадь фигуры» в других словарях:
Площадь (значение) — Площадь: площадь — это величина, измеряющая размер поверхности. В математике площадь фигуры — это геометрическое понятие, размер плоской фигуры. Площадь поверхности — это числовое свойство поверхности. Область архитектуры, открытая на сайте …… Википедия.
Территория — у этого термина существуют и другие значения. См. область (понятие). Размерность площади L² Единица измерения SIm²… Википедия.
Площадь треугольника — стандартные обозначения Треугольник — это простой многоугольник с тремя вершинами (углами) и тремя сторонами — одна часть плоскости, окруженная тремя точками, не лежащими на одной прямой, и три части, соединенные друг с другом. Вершины треугольника … Википедия.
Площадь Ленина (Петрозаводск) — Площадь Ленина Петрозаводск … Википедия
Площадь (геометрическая) — площадь, одна из основных величин, связанных с геометрическими фигурами. В простейшем случае она измеряется количеством единичных квадратов, заполняющих плоскую форму, то есть количеством квадратов, стороны которых равны длине одной единицы. Вычисление p было уже в древности … Большая советская энциклопедия.
АРЕА — одна из количественных характеристик плоских геометрий и поверхностей. Площадь прямоугольника равна произведению длин двух соседних сторон. Поэтапные участки (т.е. много соседних … Такие формы, которые можно разделить на энциклопедический словарь …
ПЛОЩАДЬ (в геометрии) — одно из количественных свойств плоских геометрий и поверхностей, где площадь прямоугольника равна произведению длин двух смежных сторон. Лестничные формы (т.е. множество … (такие формы, которые можно разделить на энциклопедические словари) AREA
AREA- площадь, квадрат, почти квадрат, и (разговорное) квадрат, пл. и площадь, жен. (Почтенный).. 1. часть плоскости, заключенная в пунктирную или кривую линию (геом.). Прямоугольный квадрат. Изогнутая область. 2. только версия. Космос, …… Словарь Ушакова.
Площадь (арка) — открытое, архитектурно организованное пространство, окруженное зелеными зданиями, сооружениями или насаждениями, являющееся частью системы других городских пространств. Пионером городского п. был дворцовый двор.
Memory Square (Chumeni) — Memory Square Chumeni Общая информация … Википедия.
Во многих случаях расчеты могут быть более сложными. Например, типичный план помещения не может состоять из простых прямоугольников или квадратов. В этом случае сложную измеряемую поверхность необходимо разделить на различные простые геометрические фигуры, прежде чем можно будет рассчитать общую площадь.
Как вычислить и обозначить площадь

Знания о том, как измерить землю, восходят к глубокой древности и постепенно сформировались в науку геометрию. Греческое слово для этого термина — «топография».
Мера длины и ширины плоской области Земли — это одна область. В математике его обычно обозначают латинской буквой S (от английского «square», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или поверхности объекта, а σ обозначает площадь поперечного сечения провода в физике. Это основные символы, но возможны и другие символы. В области прочности материалов A — это площадь поперечного сечения профиля.
Формулы расчета
Знание площади простой фигуры помогает найти параметры самых сложных фигур. Древние математики придумали формулы, которые легко вычислить. Такими фигурами являются треугольники, четырехугольники, многоугольники и круги.
Чтобы найти площади сложных фигур, их разбивают на множество простых фигур, таких как треугольники, таблицы и прямоугольники. Затем используются математические методы для извлечения уравнения области этой формы. Подобные методы используются в геометрии, а также в математическом анализе для вычисления площади фигуры, заключенной в кривую.
Треугольник
Начните с самой простой формы — треугольника. Это может быть правильный треугольник, равнобедренный треугольник или равносторонний треугольник. Возьмите треугольник ABC со сторонами AB = a, BC = b и AC = c (ΔABC). Чтобы найти его площадь, вспомните теоремы о синусе и косинусе, известные из школьной математики. Отбросив все вычисления, мы получим следующее уравнение.
- S=√p•(p-a)•(p-b)•(p-c) — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника;
- S=a•h/2, где h — высота, опущенная на сторону a;
- S=a•b•(sin γ)/2, где γ — угол между сторонами a и b;
- S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты);
- S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника);
- S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).
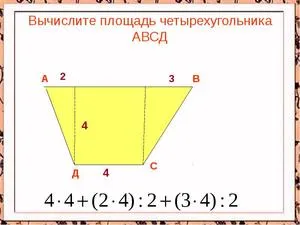
Четырёхугольник

Предположим, что четырехугольник ABCD имеет AB = a, BC = b, CD = c и AD = d. Чтобы найти площадь S любого четырехугольника, разделите его диагональ на два треугольника. Площади S1 и S2 этих треугольников, как правило, не равны.
Затем используйте формулу для вычисления и сложения. Например, S = S1+S2; однако, если четыре угла принадлежат к определенной категории, можно найти их площадь по нескольким известным типам.
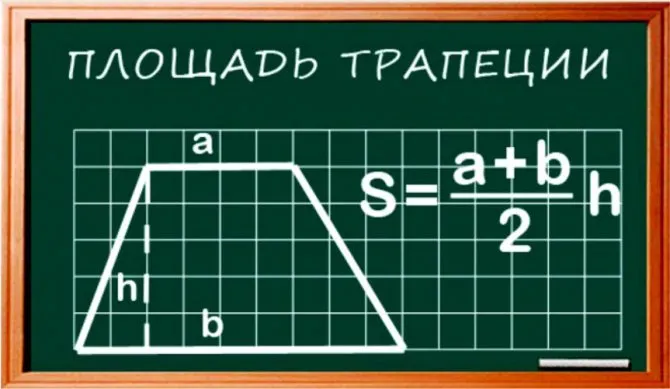
- S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции;
- S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали);
- S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ);
- S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр);
- S=a²=P²/16=d²/2, если ABCD — квадрат.
Многоугольник
Чтобы найти площадь n-угольника, математики делят его на меньшие равные фигуры, то есть треугольники, находят площадь каждого и складывают их. Однако, если многоугольник относится к категории регулярных многоугольников, используется следующая формула
S = a-n-h / 2=a²-n/4-tg (180°/ n) = P²/ 4-n-tg (180°/ n), где n — количество вершин (или ребер) многоугольника n-квадратное ребро, P — его периметр, h — депонент, т.е. часть многоугольника, проведенная под углом 90° от его центра к одному из ребер.
Единицы измерения

Существуют как систематические, так и несистематические единицы измерения. Систематические единицы относятся к СИ (Международной системе). Это квадратный метр (кв. м, м²) и его производные: мм², см², км².
Например, квадратные миллиметры (мм²) используются в электротехнике для измерения площади поперечного сечения кабеля, квадратные сантиметры (см²) — для площади поперечного сечения балки в строительной технике, квадратные метры (м²) — для квартиры или дома, а квадратные километры (км²) — для географической территории.
Однако могут использоваться и внесистемные единицы измерения, такие как сотка, ар (а), гектар (га) и акр (ас). Приведите следующие пропорции:.
Высоту прямоугольника можно представить как длину этой перпендикулярной линии. Каждый прямоугольник имеет две пары противоположностей и две высоты.
Как найти площадь фигур
Площадь геометрической фигуры — это неотрицательное число, характеризующее размер этой фигуры.
Первоначально древнегреческая геометрия (греч. «топография») занималась измерением площади и объема. Довольно много вопросов по базовой геометрии касаются именно таких вопросов.
- Площадь фигуры, заключенная между графиком непрерывной функции на интервале a,b и осью абсцисс, равна определенному интегралу этой функции на том же интервале
- Площадь фигуры, заключенная между графиками двух непрерывных функций на интервале a,b равна разности определенных интегралов этих функций на этом интервале
Как видно из графика и уравнения, площадь диаграммы, ограниченной между графиком непрерывной функции f(x) и координатами оси x в интервалах a и b, равна определенному интегралу этой функции 1. Если требуется определить площадь фигуры, состоящей из двух непрерывных функций, то вычисляются определенные интегралы обеих функций и площадь одной из них вычитается из площади другой. Разница площадей дает требуемое значение.
Интегральные вычисления также используются для определения поверхности фигуры в полярных координатах (фигура, ограниченная двумя лучами) и в трехмерном пространстве.
Свойства площади фигур
- Площадь фигуры является неотрицательной величиной
- Равные фигуры имеют равные площади
- Площадь фигуры равна сумме составляющих ее и не перекрывающих друг друга частей (свойство аддитивности).
- Площадь квадрата со стороной, равной единице измерения, равна единице (свойство нормированности)
- Площадь фигуры всегда больше площади ее части (свойство монотонности)
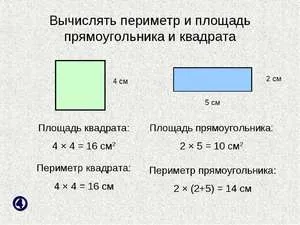
Площадь квадрата со стороной a
Площадь прямоугольника со сторонами a и b
Площадь прямоугольника со сторонами a и b, или на основе a и высоты h
S =ab*sin∠ab
Площадь ромба со стороной α, углом α между сторонами и диагоналями d1 г, г2
Площадь треугольника, основанного на a и высоте h
Площадь трапеции в зависимости от a, b и высоты h








