На уроках алгебры постепенно вводится каждая функция, включая прямые соотношения, линейные функции и функцию y =x2. Затем их определения изучаются как свойства.
Как найти область определения функции
Давайте начнем с простого определения. Функция y =f(x) — это множество значений X, для которых существует значение Y.
Давайте рассмотрим эту проблему более подробно. Каждая точка на графике функции имеет соответствующее значение.
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Просмотр графиков функций в Ox также может помочь вам понять область функции.
Что необходимо для надежного нахождения области функции? Во-первых, необходимо определить тип функции (например, корень, дробь, синус). Далее решайте уравнения и неравенства, учитывая тип функции (например, те, которые нельзя разделить, выражения, которые нельзя поставить под знак корня, и т.д.). Согласен, не слишком много, не слишком сложно. Аппаратные свойства и графики элементарных функций полезны при исследовании области действия функции. Наборы материалов и манипуляции с наборами также полезны, поскольку существуют различные наборы и их соединения и разделы.
Таким образом, чтобы найти области определения общих функций, уравнения и неравенства можно решать в одной переменной.
После этого путешествия по ключевым элементам математики многие согласятся, что найти область определения функции не так уж и сложно.
Есть даже задачи для самостоятельного определения, на которые можно искать ответы. Начните практиковаться.
Общий принцип на самых простых примерах
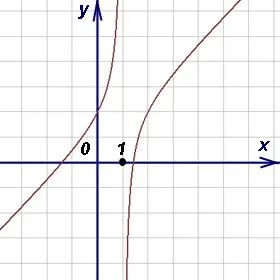
Пример 1. График функции. Знаменатель дроби не может быть равен нулю, потому что он не делится на ноль. Поэтому приравняйте знаменатель к нулю
Получить значения, которые не вписываются в поле функции: 1. Это означает, что определяющим диапазоном конкретной функции являются все значения ‘X’ от минус бесконечности до 1 и от 1 до плюс бесконечности. Это хорошо видно на графике. Приведенный здесь пример функции имеет дробный тип. В этом уроке мы рассмотрим решения для всех распространенных типов функций.
Пример 2.Как найти площадь функции y, равной квадратному корню из x минус 5 (подвыражение x минус 5)? Выражение, включающее подкорень, должно быть неотрицательным, поэтому необходимо решить неравенство
Перенос члена в другую часть неравенства с противоположным знаком дает равносильное неравенство с тем же знаком неравенства (можно зачесть все основные свойства неравенства). Вычтите минус 5 и получите следующее неравенство
Получено решение: областью функции являются все значения x больше или равные 5 (или x принадлежит интервалу 5, включая бесконечность).
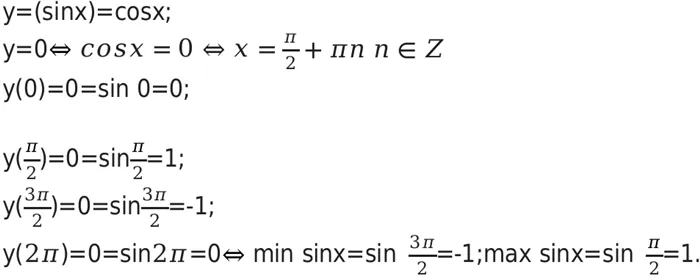
На диаграмме выше показана часть числовой оси. Область рассматриваемой функции заштрихована, причем в «положительном» направлении штриховка продолжается бесконечно вдоль самой оси.
Область определения корня n -й степени
Для функций порядка n, т.е. когда функция задана выражением, а n — натуральное число:.
Если n четное, то областью действия функции является сумма всех неотрицательных действительных чисел, т.е. 0. +∞,.
Если n нечетное, то область применения функции — сумма всех действительных чисел, т.е. -∞. +∞.
Пример 3.Найти область функции.
Решение. Из определения следует, что если слагаемое неотрицательно, то имеют смысл корни четного порядка. Поэтому решите неравенство
Это квадратное неравенство.
Используйте следующее уравнение для нахождения характеристики.
Используя тип, найдите корень квадратный из 3:.
Найденные точки делят арифметическую прямую на три промежутка.
Знак квадрата 3 (больше или меньше нуля) совпадает со знаком коэффициента A во всех точках промежутка
и он противоположен знаку коэффициента A во всех точках пространства.
В нашем случае квадратный трицикл неотрицателен во всех частях пространства, так как существует отрицательный коэффициент a = -1.
Следовательно, площадь функции равна -1? 1.
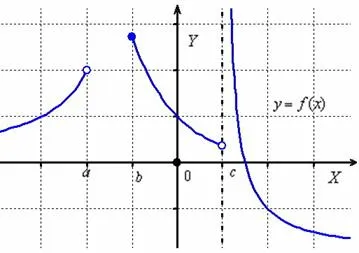
Заштрихованная область числовой линии приведенной выше конструкции является областью функции.
Уравнение не имеет действительных корней. Однако функция определяется только вещественными числами. Следовательно, область этой функции является линией целых чисел, или, что то же самое, суммой действительных чисел r, или, что то же самое, ∞? +∞.
Область определения для суммы, разности и произведений числовых значений
Чтобы правильно определить конкретный сектор, необходимо знать следующие утверждения. Если функция вычисляется, используя сумму: ﻟ f_+f _+ ﻟ ldots f_ \ text< или >\ mathrm = f_+f _+\ ldots f_ \
Область определения имеет следующий формат: Ј mathrm (Ј mathrm) = \ mathrm \ left (f_ \ right) Ј left (f_ \ right) ldots f_ \ left (f_ \ right) Ј left (f_ \ right) Ј left (f_ \ right).
Пример суммы значений: получим уравнение: ɑ y = x^+x+5+t g x \ \ \.
Решение: уравнение выражается в виде суммы многих значений. Степень равна 7, а экспонента равна единице.
Все области идентификации TG являются вещественными числами.
ОТВЕТ: для определенной функции, пересечение ряда областей или вещественных чисел, которые отличаются от Z \\\\ pi / 2+ \ pi \ cdot n \
Примеры различных значений:.

Примеры чисел:.

Сложные функции х и y и их область определения и значения
Сложные функции имеют следующий вид
Пересечение двух множеств является областью функции сложного типа.
\ Представьте функцию в виде \ mathrm = f_ \ left (f _ (⌘ mathrm) ⌘ right).

Используйте определения, изученные в этом курсе.
Это свидетельствует о системе неравенства.
![]()
ОТВЕТ: все действительные числа, кроме нуля.
Область определения функции в виде дробного значения
Если функция задана в виде дроби. Переменная величина находится в знаменателе. Поэтому область определения — вещественные числа. Исключение составляют числа, вызывающие нигилизм знаменателя.
Пример 1: ǫ y = \ frac \. Решите уравнение, чтобы определить требуемое значение области принятия решения. Это ⌘ — \ infty; -4 \ cup-4;+ ⌘ infty \
Пример №2: ⌘ y = \ frac> \,.
Необходимый регион: ⌘ — \ infty; -1 \ cup-1; 1 \ cup 1;+\ infty.⌘
Пример №3. \ y = \ cos x+\ frac-4> \.
Первая сумма имеет диапазон наборов действительных чисел. Второй — все числа, кроме -2 и 2, уменьшая знаменатель до нуля. Область определения должна удовлетворять условиям двух совокупностей и быть равна действительным числам, кроме -2 и 2.
Я не буду говорить о таких более простых функциях, так как любой человек вполне может увидеть точки, которые не находятся в области определения. Давайте рассмотрим самые важные фракции.
памятка по теме «Область определения функции» консультация по алгебре (9 класс) на тему
Область определения функции — это множество наборов значений выражения x, описанных в правильной части уравнения для x.
Область определения функции — это множество значений членов x, для которых могут быть выполнены все действия, предусмотренные правильной частью уравнения функции.
Помните, если правая часть уравнения функции является дробью.
— Тире в дроби означает энергию деления.
Поэтому значения аргумента X, для которых обнуляется знаменатель, должны быть исключены из области, определяющей такую функцию.
Найдите область, определяющую функцию.
Функция представляет собой дробь. Поскольку она не может делиться на ноль, она исключает из области определения значения переменной x, для которых дробный знаменатель равен нулю.
Таким образом, для x = 0 и x = 4 порядок дробей равен нулю. Давайте исключим эти значения переменной x.
Помните, что правая часть уравнения функции — это квадратный корень.
— Квадратные корни определены только для неотрицательных чисел (положительных и нулевых)!
— Квадратные корни можно экспортировать только для неотрицательных чисел.
Поэтому область определения такой функции должна включать значение переменной x, для которой Секорд получает неотрицательное значение.
Найдите область, определяющую функцию.
Правая часть уравнения функции является квадратным корнем. Поскольку квадратный корень можно извлечь только из неотрицательных величин, найдите значение переменной x, для которого уравнение с коэффициентом 2х-5 неотрицательно.
Представим все решения этого неравенства координатными прямыми.
Полученное множество является полем функции.
Каково поле функции? Мы можем это увидеть?
Какова площадь?» Давайте ответим на вопрос.
Слово «домен» встречается не только на уроках математики. Судите сами. Вы не встретите таких фраз, как «меланская область» или «ростовская область». Попробуйте определить эти пункты.
Под «чернилами» понимается часть человеческого тела, на которую был нанесен удар, или любая другая ударно-механическая часть с болевыми ощущениями.
Ростовская область» — это часть земной поверхности, на которой территориально расположены населенные пункты и природные объекты вблизи Ростова Донского.
Обратите внимание на сходство между этими определениями. И это сходство дает нам основание думать, что «регион» является частью чего-то.
А какова область определения функции?
Это также место. Часть действительной линии x, где находится значение переменной x (простым словом, число), где левая часть уравнения функции имеет смысл.
По теме: методические разработки, презентации и конспекты
Систематическая разработка обобщающего курса 11 класса по теме «Область определения функций
Систематическая разработка сжатого урока для 11 класса по теме «Область определения функций».
Урок алгебры в 9 классе по теме «Область определения функций».
Постройте график функции y = | x |.

Область определения функций. Урок алгебры в 9 классе.
Урок 1, Силовые функции, Глава 3, Пособие по алгебре 9, Ш.А. Алимов.
Презентация курса «Разрешение неравенства. Область определения функций».
Данная презентация прекрасно подходит для учителей и конспектов учителей при систематизации и обобщении знаний по теме «Решение функциональных задач». Все фазы включают.

Самостоятельная работа по теме «Определение функций».
Самостоятельная работа по теме «Область определения функций».
Функции. Область определения функции.
Примеры зависимостей между переменными фактического процесса от соответствующих отделов. Определение функций. Построение и чтение функций.
Презентация: примеры зависимостей между переменными фактического процесса от соответствующего отдела. Определение функций. Построение и чтение функций.
Математика — это точная наука. Поэтому каждое упражнение имеет решение, каждое число имеет сигнатуру, а каждая функция имеет область определения. Мы поговорим о последнем и узнаем, как найти область определения функции.
Область определения функции с логарифмом
Третьей распространенной функцией является логарифм. В качестве примера разработайте натуральный логарифм, который встречается примерно в 99 примерах из 100. Если функция содержит логарифм, то ее область определения должна содержать только те значения ‘x’, которые удовлетворяют неравенству. Если логарифм находится в знаменателе: член дополнительно накладывается (приводится).
Нахождение области функции
Решение: в соответствии с вышеизложенным, создайте систему для решения проблемы.

Графическое решение для чайников: ответ: область решения:.
Хотелось бы отметить еще один технический момент — у меня нет деления шкалы или оси. У меня вопрос: как сделать такой план для заметок на пледе? Можно ли точно измерить расстояние между точками в клетке по шкале? Конечно, в масштабе все выглядит более нормально и строго, но схематичный дизайн, который в первую очередь отражает ситуацию, тоже вполне приемлем.
Нахождение области функции
Для решения проблемы можно воспользоваться методом предыдущего параграфа — проанализировать, как притча соотносится с осью бездны. Ответ находится в конце урока.
Как видите, в области логарифмов все похоже на задачу о квадратном корне. Функции (квадратные трели в примере №7) определяются интервалами, функции (квадратные биноминанты в примере №6) — пробелами. Стыдно сказать, что функции типа определяются целочисленными строками.
Полезная информация: функции типа интересны и определяются на всей числовой прямой, кроме точек. Согласно логарифмам, ‘2’ можно получить как множитель вне логарифма, но чтобы функция не изменилась, под символом Modulo нужно поставить ‘x’. Это еще одно «практическое применение» Modulus =). Это необходимо делать в большинстве случаев, когда требуется устранить грубые силы. Например, если основание силы явно положительное, нет необходимости использовать символ коэффициента; достаточно скобок.
Чтобы избежать повторения, усложните проблему.
Нахождение области функции
Решение: функция имеет и корень, и логарифм.
Выражение для слагаемых должно быть неотрицательным:, а выражение под логарифмом должно быть строго положительным:. Поэтому система должна быть решена.
Многие из вас хорошо или интуитивно знают, что решение системы должно удовлетворять всем условиям.

Глядя на положение притчи по отношению к осям, мы приходим к выводу, что неравенства встречаются в пространстве (оттенки синего). Очевидно, что неравенство соответствует «красной» полусистеме.
Решением системы является пересечение этих пространств, так как оба условия должны выполняться одновременно. Общий интерес» соблюдается на полпути.
Области определения функций с тангенсами, котангенсами, арксинусами, арккосинусами
Перед изучением параграфов рекомендуется вернуться к первой статье в графике и обновить визуальную и подробную информацию о функциях, перечисленных в заголовке.

Если речь идет о конкретной функции, то эта точка исключается из области определения, где z — ряд чисел последовательности. В частности, как описано в статье Графики и свойства элементарных функций, функция имеет следующие значения То есть, касательная область идентификации.
Постарайтесь не быть слишком склонным к самоубийству:.
Нахождение области функции
Решение: в данном случае следующие точки не входят в область определения.
Бросьте «2» слева в знаменатель справа.

Результат: ответ: определение региона:.
В принципе, ответ можно записать как объединение бесконечного числа пробелов, но построение очень сложно.
Аналитическое решение идеально совпадает с геометрическим преобразованием графика. Если аргумент функции умножить на 2, график уменьшится вдвое. Обратите внимание, что продолжительность функции сокращается вдвое, а точка прерывания удваивается. Тахикардия.

Аналогичная история и с тренером. Если функция включена, то точка исключается из ее области определения. В частности, для автоматических функций принимаются следующие значения. То есть, следующее.
Миниатюрные для независимых решений:.
Нахождение области функции
Этого стоило ждать, потому что, как обычно, лук и стрелы являются главными героями математического концерта, и, помимо нахождения определяющей области, вы сможете научиться решать (или повторять) двойное неравенство.
Если задействована функция или ее область определения ограничена двойным неравенством.
Нахождение области функции
Решение: создайте двойное неравенство:.
Двойные неравенства очень похожи на «обычные» простые неравенства. Конечная цель преобразования заключается в том, чтобы в середине остался только «x».
Сначала удалите устойчивое в середине, убрав «три» из каждой части неравенства.
Умножьте все три части неравенства на -1. Поскольку мультипликатор отрицательный, знаки самого неравенства должны быть «перевернуты».
Умножьте все части неравенства на
Запишите свой ответ, повторяя знаки неравенства в обычном порядке, как они стоят в арабском языке от «один» до «два» справа налево.
Ответ: область определения: или
Простой последний пример для самостоятельного решения: или








