Каждый стол можно рассматривать как усеченный треугольник с линиями сечения, параллельными основанию треугольника. Важно Обратите внимание, что некоторые задачи с трапециями можно решить таким образом (создавая дополнительные таблицы в треугольнике) и доказать определенные теоремы.
Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
Во всех следующих математических записях буквенные обозначения верны.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1г, г2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Найти периметр трапеции
Можно вводить числа или дроби (-2,4, 5/7, …) .
ABC +∠BAD= 180° и modc +∠BCD= 180° в год похвалы.
2. Если цикл может быть зарегистрирован в равнобедренной таблице, то его сторона равна средней линии трапеции.
6. если цикл может быть зарегистрирован в равнобедренной таблице, то квадрат высоты равен произведению оснований трапеции.
7. сумма квадратов диагоналей равна произведению суммы квадратов боковых сторон и удвоенного основания трапеции.
AC 2 + BD 2 = AB 2 + CD 2 + 2BC -AD
8. прямая, проходящая через средние точки оснований, перпендикулярна основаниям и является осью симметрии стола.
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg a = b + 2 c cos a
b = a — 2 h ctg a = a — 2 c cos a
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d1 2 – c 2 | b = | d1 2 – c 2 | c =√d1 2 – ab |
| b | a |
Формулы длины средней линии равнобедренной трапеции:
m = a -h ctg a = b + h ctg a = a-√c2 -h 2 = b +√c2 -h 2
Формулы определения длины высоты равнобедренной трапеции:
В исходных данных: все стороны
Чтобы найти высоту трапеции, как правило, необходимо воспользоваться следующим человеком
n = √(c 2 — ((a -c)2 + c 2 -d 2)/(2(a -c))2). Номер 1.
Не самая короткая, но, похоже, очень редкая проблема. Обычно можно использовать другие данные.
Тех, кто расскажет вам, как найти высоту трапеции изошеллы, в том же государстве будет гораздо меньше.
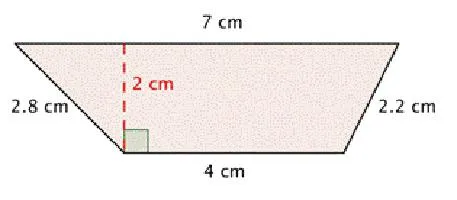
Прямоугольный стол называется угловым, одна из сторон которого равна 90 0. Если три другие стороны известны, рассмотрим пример нахождения стороны трапеции.
Виды трапеций
Таблица изошеля — это разновидность трапеции с равными сторонами.
Его также называют таблицей изошелл или таблицей изошелл.
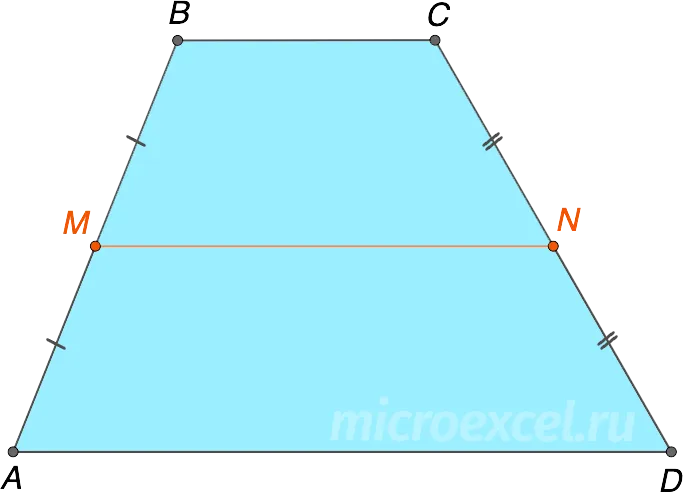
Прямоугольный стол — это стол с прямыми углами по бокам.
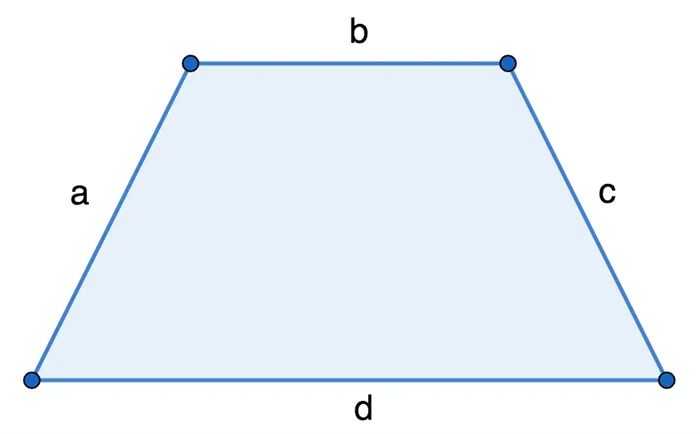
Элементы трапеции

a, b — основания трапеции (a параллельно b); и
m, n — стороны трапеции; и
H — высота стола (отрезок, соединяющий основания и перпендикулярный им), и
MN — медианная линия (отрезок, соединяющий средние значения сторон).
Площадь трапеции

- Через полусумму оснований a, b и высоту h : S = \frac\cdot h
- Через среднюю линию MN и высоту h : S = MN\cdot h
- Через диагонали d1г, г2 и угол ( \sin \varphi ) между ними: S = \frac d_ \sin \varphi>
Важно отметить, что только одна сторона должна быть перпендикулярна основанию. Если оба присутствуют, таблица автоматически становится квадратной.
Как находить стороны трапеции
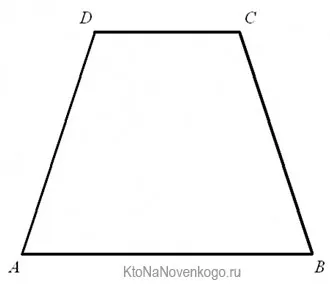
Стол (от греческого table, «стол», bank, «стол, еда») — это четырехугольник с параллельными противоположными точными сторонами.
Этот стол представляет собой четырехугольник с параллельными противоположными сторонами.
ПРИМЕЧАНИЯ. В данном случае прямоугольник является частным случаем банкира.
Параллельные стороны называются основаниями трапеции, а другие стороны — гранями.
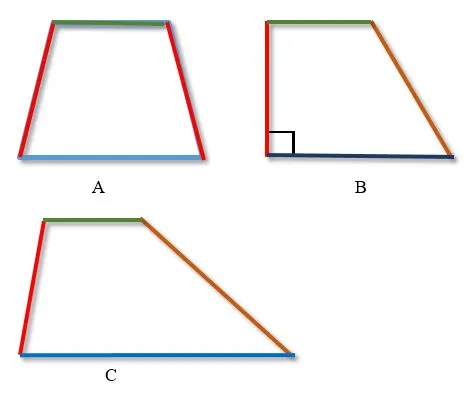
. Красный и коричневый — боковые стороны, зеленый и синий — основания трапеции.
A — равнобедренный стол B — прямоугольный стол C — равносторонний стол
У трех равносторонних сторон все стороны разной длины, а их основания параллельны.
У равнобедренных столов равные стороны и параллельные основания.
В прямоугольных столах основания параллельны, одна сторона перпендикулярна основанию, а другая сторона наклонена к основанию.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Трапециевидные углы бывают острыми, прямыми и тупыми. Только два угла являются прямыми.
Прямоугольные столы имеют два правильных угла, два других — острый и тупой. Другие типы трапеций имеют два острых и два тупых угла.
Тупой угол трапеции принадлежит наименьшему основанию, а острый угол принадлежит наибольшему основанию.
Каждый стол можно рассматривать как усеченный треугольник с линиями сечения, параллельными основанию треугольника. Важно Обратите внимание, что некоторые задачи с трапециями можно решить таким образом (создавая дополнительные таблицы в треугольнике) и доказать определенные теоремы.
Как найти стороны и диагонали трапеции
Чтобы найти стороны и диагонали трапеции, используйте следующую формулу
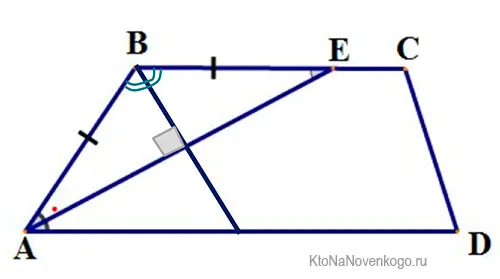
Символизм, как показано на схеме, относится к вышеперечисленным типам.
a — меньше основания трапеции b — больше основания трапеции c, d — боковые стороны трапеции1h2 -диагонали диагоналей.
Сумма квадратов диагоналей трапеции равна удвоенному произведению суммы квадратов основания и боковых сторон трапеции (уравнение 2).
Площадь трапеции
где a и b — параллельные основания трапеции; c и d — боковые стороны трапеции; m — средняя линия трапеции; r — радиус вписанной в трапецию окружности; S — площадь трапеции; d — площадь трапеции; m — площадь трапеции; s — площадь трапеции.
Важно отметить, что только одна сторона должна быть перпендикулярна основанию. Если оба присутствуют, таблица автоматически становится квадратной.
Трапеция формулы
Трапеция — это прямоугольник с двумя параллельными сторонами (основание) и двумя непараллельными сторонами (боковые стороны).
Каждая трапеция характеризуется основаниями α и β, боковыми сторонами γ и δ, высотой h и средней линией L (см. схему). Эти характеристики используются типами трапеций при вычислении площади и периметра.
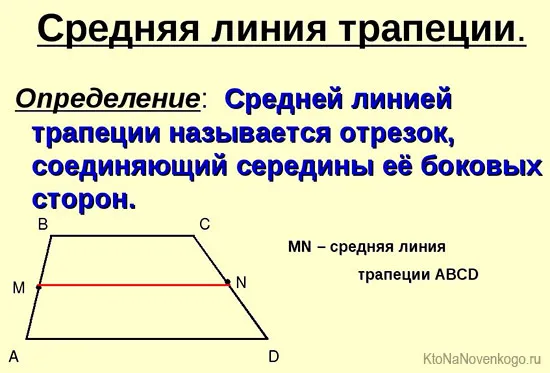
Средняя линия трапеции соединяет центры ее ребер.
Площадь трапеции S можно вычислить, зная ее основание и высоту h, проведенную на одном из ребер основания: см. рисунок.
Площадь трапеции S также можно вычислить, зная среднюю линию L и высоту h:.
Для двух диагоналей d1 и г2 и их углы a, площадь стола также может быть вычислена:.
Поделитесь статьей с одноклассниками: «Площадь и периметр типа TRAPEACE, осевая линия таблицы».
Если вы копируете материал с сайта, ссылка на источник обязательна. Пожалуйста, уважайте труд тех, кто вам помогает. Нашли ли вы ошибку? Выделите текст и нажмите Ctrl+Enter.
Из точки C проведите высоту SK, чтобы получить правильный треугольник SK и правильный треугольник ABC. Так как у прямоугольника противоположные стороны равны SK=AB =12 см и AK=BC =1 см.
Определение трапеции
Трапеция — это четырехугольник с двумя параллельными сторонами и двумя непараллельными сторонами.
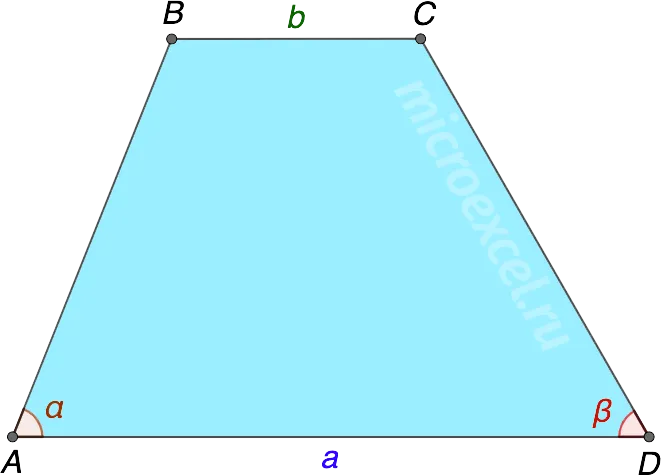
Параллельные стороны называются основанием (AD и BC), а две другие стороны — боковыми сторонами (AB и CD).
Угол основания трапеции — это внутренний угол трапеции, образованный основанием и боковыми сторонами трапеции. A и B.
Трапеция описывается перечислением ее вершин (обычно ABCD). Затем основание символизируется маленькими латинскими буквами. a и b.
Средняя точка трапеции (MN) — это часть, соединяющая середины ее сторон.
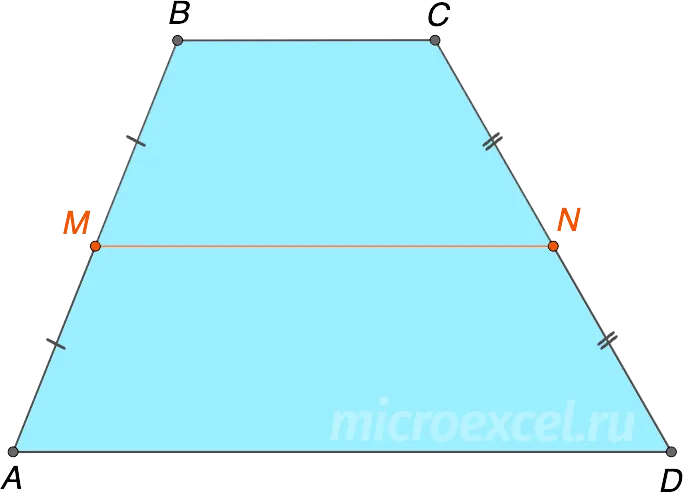
Высота трапеции (h или BK) — это вертикальная линия, проведенная от одного основания к другому.
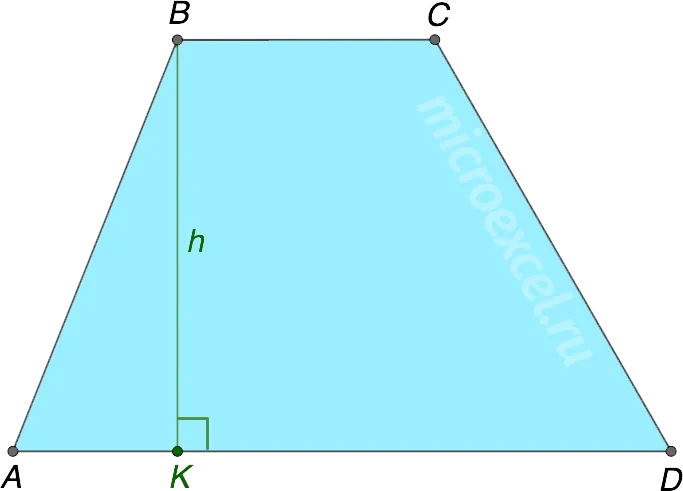
Виды трапеций
Равнобедренная трапеция
Трапеции с равными сторонами называются трапециями-изоподами.
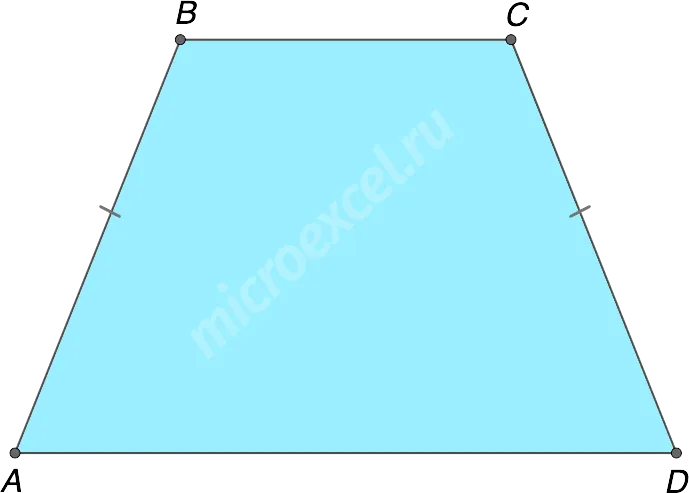
Прямоугольная трапеция
Трапеция, у которой оба угла расположены на одной стороне, называется прямоугольной трапецией.

Разносторонняя трапеция
Если стороны стола не равны и угол основания не правильный, то стол является приставным.
Свойства трапеции
Перечисленные ниже свойства применимы ко всем типам трапеций. Свойства для равнобедренных треугольников и прямоугольных трапеций описаны в отдельных публикациях на нашем сайте.
Свойство 1
Сумма углов трапеции, касательных к одной и той же стороне, равна 180°.
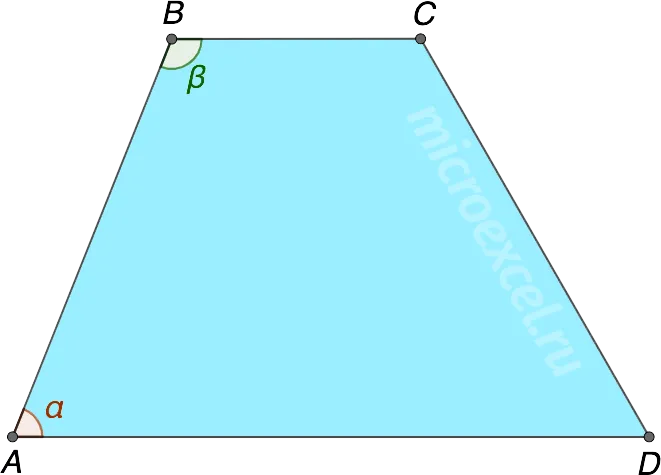
Свойство 2
Центральные линии трапеции параллельны ее основанию и равны половине их суммы.

Свойство 3
Центральные соединительные диагонали трапеции лежат на средней линии и равны половине разности их базовых сторон.
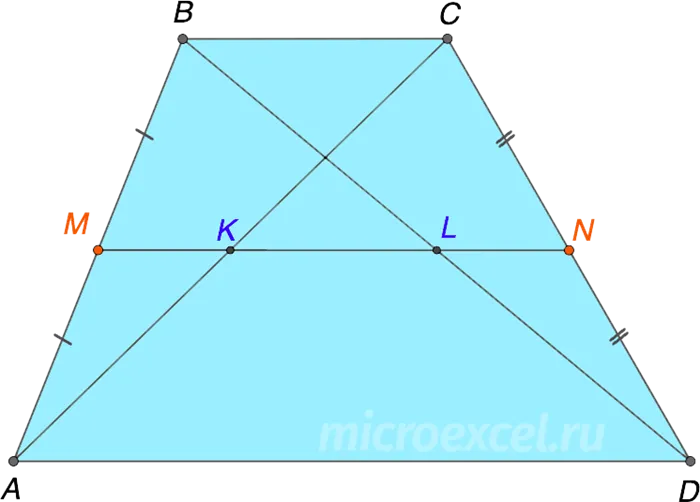
- KL – отрезок, соединяющий середины диагоналей AC и BD
- KL лежит на средней линии трапеции MN
Свойство 4
Пересечение диагоналей трапеции, продолжение ее боковых сторон и середина основания лежат на одной прямой.
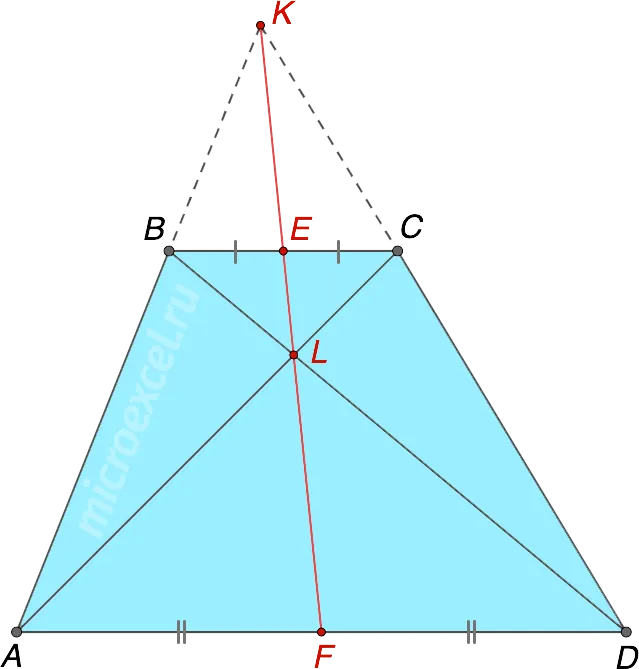
- DK – продолжение боковой стороны CD
- AK – продолжение боковой стороны AB
- E – середина основания BC, т.е. BE = EC
- F – середина основания AD, т.е. AF = FD
Если сумма углов одного основания равна 90° (т.е. ∠DAB + ∠ADC = 90°), то боковые продолжения трапеции пересекаются под прямым углом, а часть, соединяющая средства оснований (ML), равна половине их разности.
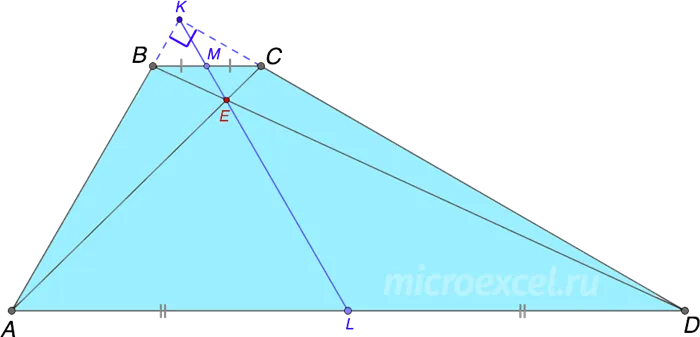
Свойство 5
Диагональ банкира делит его на четыре треугольника, два из которых (основания) подобны, а два других (стороны) имеют равные площади.
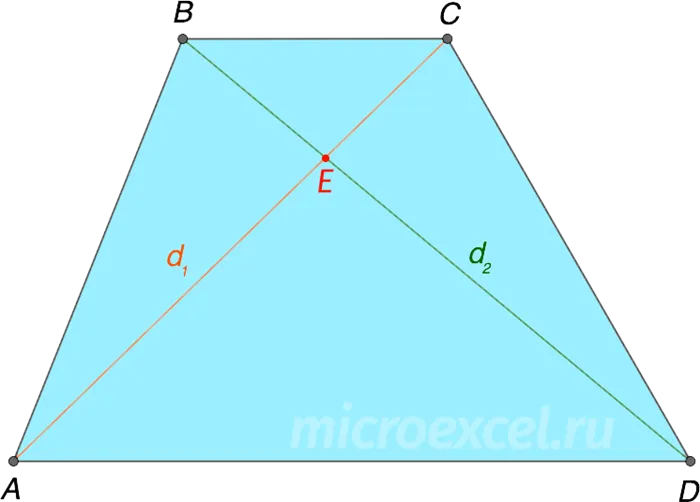
Свойство 6
Сечение через точку пересечения диагоналей, параллельных основанию трапеции, может быть выражено через длину основания.
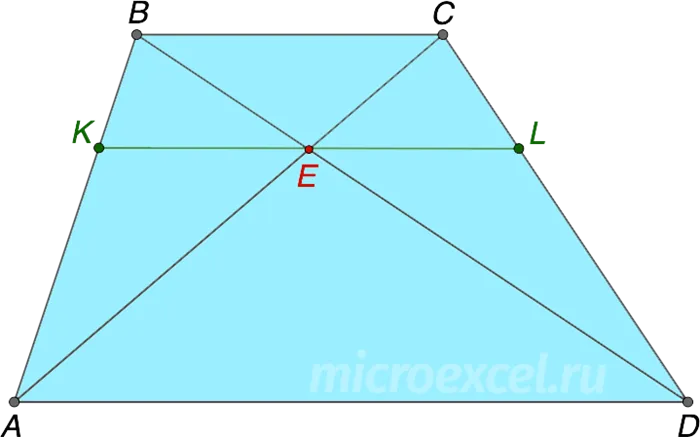
Свойство 7
Биссектрисы углов трапеции с равными сторонами перпендикулярны друг другу.
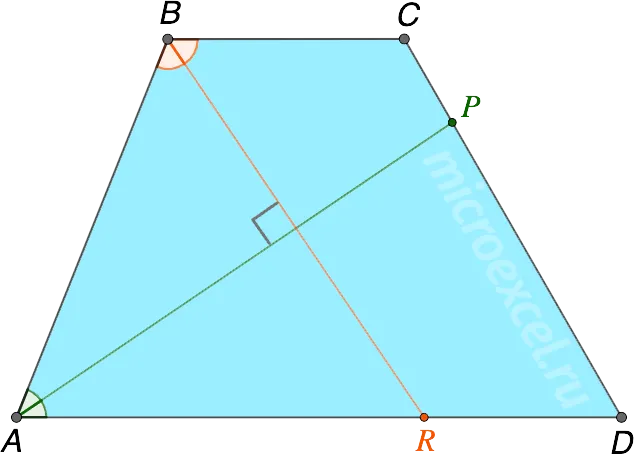
Свойство 8
Окружность можно вписать в таблицу только в том случае, если общая длина ее основания равна общей длине ее сторон.
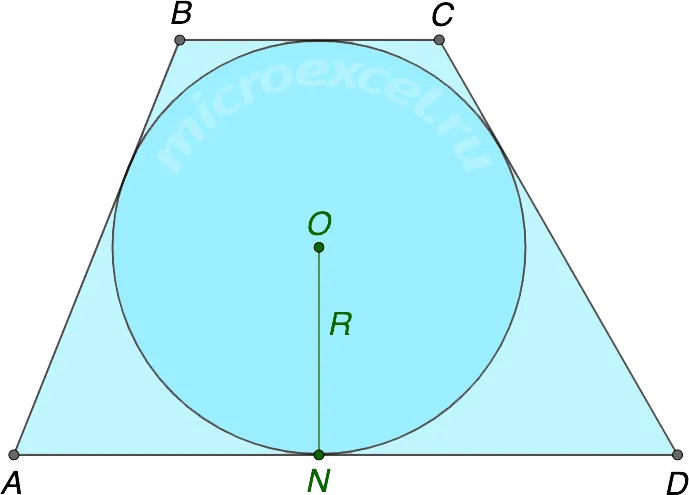
Параллельные стороны называются основанием (AD и BC), а две другие стороны — боковыми сторонами (AB и CD).
Видео
Высота трапеции через ребро вычисляется по формуле. $ h = sqrt)^ 2> $, где $a$ — наибольшее основание- $d$ — наименьшее основание- $b$ — первое ребро- $c$ — второе ребро.
База задач Предположим, что имеется стол, у которого $a$ и $d$ равны $4,5$ и 3500,5$ см, а стороны $b и c$ равны $3500 и 3500sqrt2$ см. Найдите высоту $h$ стола. Решение: используйте приведенную выше формулу: $ h = sqrt)^ 2> = sqrt> = 2$см. проверьте полученное значение с помощью калькулятора. Результат тот же, поэтому проблема решена правильно.
Рассмотрим, как найти сумму длин всех сторон этого четырехугольника.
По сторонам равнобедренной трапеции
Если известны ребра этого четырехугольника с одинаковыми сторонами, мы можем найти его P по следующей формуле.
Через среднюю линию
Поскольку средняя линия трапеции равна половине суммы ее оснований, уравнение P можно выразить как
где l — средняя линия фигуры.
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d1 =√a2+d2-2ad-cosβ
d2 =√a2+c 2—2ac-cosα
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
3. Формула длины диагоналей через высоту:
d1 =√h2+(α—h—ctgβ)2=√h2+(β+ h—ctgα)2
d2 =√h2+(α—h—ctgα)2=√h2+(β+ h—ctgβ)2
4. форма длины диагонали по сумме квадратов диагоналей: d1=√c2+d2 + 2ab —d 22 d2=√c2+d2 + 2ab —d 12
Периметр ABCD = AB + B + CD + AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона AB = 5 см, BC = 7 см, AD = 10 см, а длина стороны CD неизвестна.
Происхождения слова
Первое упоминание об этой диаграмме относится к работе известного древнегреческого математика Евклида.
В его книге «Доказательства» этот термин используется для описания абсолютно всех четырехугольников, а не прямоугольников.
Если вы не помните, прямоугольник — это четырехугольник с противоположными сторонами, параллельными друг другу. В классическом смысле эта форма имеет вид
Интересно, что известные формы (квадрат, прямоугольник (что это?) и ромб (что это такое?)) также являются частными случаями прямоугольников. Действительно — их противоположные стороны параллельны друг другу.
И оказалось, что Евклид в целом был прав. Все, что нам нужно сделать, это разделить все четырехугольники на две большие категории (прямоугольники и таблицы).
Кстати, само слово trapecia также греческого происхождения. В древности его произносили как «трапедион». В переводе это означает «стол для еды». Таким образом, слово «трапеза», синоним любого приема пищи, также происходит оттуда.
Стороны трапеции
Аспекты требизоида имеют следующие названия
- Основания трапеции – стороны, которые располагаются на параллельных прямых.
- Боковые – стороны, которые не находятся на параллельных прямых.
Примите это с помощью плана.
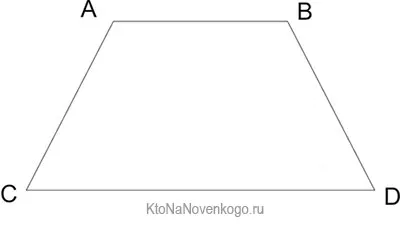
В этом случае аспекты AB и CD параллельны друг другу. Это означает, что они являются базовыми. Напротив, очевидно, что AC и BD не параллельны. Поэтому они являются сторонами.
Кстати, расположение сторон не зависит от положения самой фигуры. Даже в таких положениях.
Параллельные грани остаются основаниями, а непараллельные грани — сторонами.
Равнобедренная и прямоугольная трапеции
Изученный нами вариант трапеции является наиболее распространенным типом геометрической формы. Однако есть и особые случаи.
Равнобедренный стол — это стол с равными внешними (непараллельными) сторонами. Его также называют таблицей изошелл или таблицей изошелл.
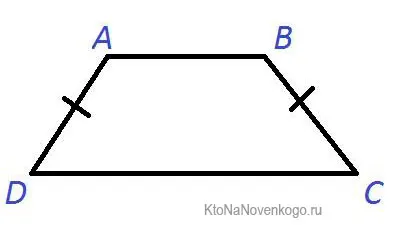
Этот пример графически показывает, что стороны ad и bc равны друг другу. Это обозначается маленькой черточкой.
Прямоугольные столы — это столы, одна из сторон которых образует прямой угол.
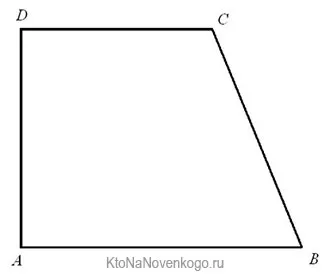
В данном примере угол между DAB и ADC равен прямому углу, т.е. 90 градусов. Поэтому стол называется прямоугольным.
Важно отметить, что только одна сторона должна быть перпендикулярна основанию. Если оба присутствуют, таблица автоматически становится квадратной.








