Чтобы найти числовое значение этой дроби, разделите известное количество на дробь или аналогичное число. Чтобы найти числовое значение этой дроби, разделите известное количество на ее числитель и умножьте на знаменатель.
Основные определения
Процент — это один сантиметр от любого числа. Синус — это процент.
Чтобы узнать, как процент переводится в десятичную точку, уберите знак % и разделите известное на 100. Например, 18% — это 18:100 = 0,18.
Чтобы преобразовать натуральное число или десятичную дробь в проценты, умножьте дробь на 100 и добавьте символ %. Например, 0,18 = 0,18-100% = 18%.
Выразить дроби в процентах очень просто. Чтобы перевести его, сначала переведите его в дробные дроби, а затем используйте предыдущее правило для перевода дробных дробей в проценты.
Проценты: правила
Рассмотрим четыре известных способа нахождения процентов.
Занимайтесь математикой вместе с преподавателем на нашем онлайн-курсе математики для детей и подростков!
Нахождение одного процента от числа
Существует несколько способов найти проценты от числа.
Первый метод.
Умножьте полученное значение на искомое количество процентов.
Например: найдите 12% от числа 48.
Второй метод.
Переведите процент в десятичную точку.
Умножьте число на полученную десятичную точку.
Снова найдите 12% из 48, но другим способом.
Представьте, что вы идете в магазин, чтобы купить шоколадные конфеты. Обычно он стоит 250 рублей, но сегодня действует скидка 15%. Если в магазине есть дисконтная карта, то шоколад стоит 225 рублей. Что лучше: скидка или карта?
250:100 = 2,5 — это 1% от стоимости шоколада.
Таким образом, 2,5 х 15 = 37,5 — 15%.
ОТВЕТ: рентабельность выше, если вы пользуетесь скидкой 15%.
Составление пропорции
Равенство двух процентов называется отношением.
Прочитайте: А относится к В, как Г и Д. Также важно помнить, что произведение крайних членов равно произведению промежуточных членов. Чтобы найти неизвестное этого равенства, нужно решить простейшее уравнение.
Рассмотрим его пример. Насколько выгодно покупать спортивную футболку за 1390 рублей, потому что в День святого Валентина в магазине действует скидка 14%?
Узнайте, насколько увеличивается прибыль, т.е. на сколько рублей, т.е. скидка 14%. Пусть цена блузки составляет 100%. Следовательно, 1390 рублей = 100%. Тогда 14% — это X рублей. Вы получаете соотношение:.
Умножьте на крест и найдите X:.
Ответ: дисконтированная выгода составляет 194,6 руб.
Соотношения чисел
Можно использовать простые дроби. Например, 10% — это одна десятая часть от общего количества. Чтобы найти 10% от числа A, соберите примеры процентного содержания чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Вопрос по упражнению. В «черную пятницу» мы нашли отличную куртку со скидкой 25%. В обычный день она стоит 8 500 рублей, а сейчас — всего 6 400 рублей. Есть ли у вас достаточно денег, чтобы купить его?
Это означает, что вы должны заплатить 75% от первоначальной цены.
75% составляет 3/4 от числа, поэтому 8500:4 x 3 = 6375 (рублей).
ОТВЕТ: куртка стоит 6 375 рублей, поэтому в ней несколько глав.
В классе 12 комсомольцев. Это означает, что существует 3 /5 всех учащихся в классе. Сколько учеников в классе?
Нахождение числа по его дроби
Сформулируйте задание на нахождение чисел с числовыми значениями.
Есть дробь — она говорит нам, какая часть нашего числа дана.
Существуют числа, которые равны определенной дробной части числа.
Вы уже знаете, как найти дробную часть числа. Вспомните, как это делается.

Чтобы найти долю числа, нужно умножить исходное число на дробь. Это даст вам значение для дробной части числа.
В этой задаче была известна часть целого числа и дробь, полученная из него. Часть номера осталась неизвестной.
В задаче этого урока часть числа уже известна, но нам нужно найти целое число.
Чтобы найти его, мы можем составить уравнение, подобное тому, что изображено на рисунке выше. Единственное различие — это переменные, которые мы знаем.
Мы решаем это уравнение и переносим известный нам множитель, или дробь, в правую часть.
На предыдущем уроке мы узнали, как делить на дробь. Помните, что для этого нужно умножить на обратную дробь.
Другими словами, мы имеем формулу неизвестного числа.
Сформулируйте правило. Чтобы найти часть числа, разделите известную часть числа на его дробь.

Число \(ˈ mathbf> \) равно 21, и вы находите исходное число.
В качестве решения разделите известную часть числа на дробь. Например, разделите 21 на ⌘ (⌘ mathbf> \)
\ (⌘ mathbf> \) находит исходное число из числа, равного 12.
Чтобы решить эту задачу, разделите данную часть числа на данную пропорцию. Другими словами, 12 делится на ߡ (⌘ mathbf> \).
Не всегда можно разделить часть числа на числитель определенной дроби. В таких случаях вместо целого числа в ответе вы получаете дробь или целое число.
Число \ (⌘ mathbf> \) равно 11 и находит исходное число.
Остальной ответ тот же — разделите дробь на число и получите результат, если значение дроби ⌘ (⌘ mathbf> \) равно 11.
Чтобы получить ответ, нам нужно извлечь целое.
Нет никакой гарантии, что части данного нам числа не находятся в одинаковой пропорции.
Не стоит бояться такого случая, а нужно придерживаться алгоритма деления части числа на его долю.
Найдем целое число, в котором число \(\ mathbf> \) равно \(\ mathbf> \).
Чтобы решить этот пример, разделите \(⌘ mathbf> \)-ю часть числа на \(⌘ mathbf> \)-ю дробь.
Все начальное число равно \(\ mathbf> \).
Войдя в систему или зарегистрировавшись, вы можете пройти тест и получить результат.
Нахождение числа по проценту
Теперь предположим, что вам дали определенное процентное число, и вам нужно узнать, от какого числа был взят процент.
Помните, что проценты — это способ записи десятичных дробей.
Это означает, что для перевода процентного значения в десятичное число, которое оно представляет, необходимо разделить процентное значение на 100.
Поэтому, чтобы решить этот тип задачи, необходимо преобразовать процент в десятичную дробь, а затем сделать то же самое. Другими словами, разделите число на дробь.
Мы знаем, что зарплата работника увеличилась на 2 000 рублей, то есть на 25%. Какова была начальная зарплата работника?
Преобразуйте процент в дробь: ߡ(ߡ mathbff ߡ)
Разделите число на дробь: \(\ mathbff \)
ОТВЕТ: Первоначально зарплата работника составляла 8000 рублей.
Чтобы найти число в процентах, необходимо преобразовать проценты в десятичные дроби, а затем разделить часть числа на полученную дробь.
Считается, что девять процентов от числа равны 81. Вам нужно найти целое число.
Первый шаг — преобразовать проценты в десятичные числа.
Второе действие — разделить число на дробь.
Ответ — 900.
Войдя в систему или зарегистрировавшись, вы можете пройти тест и получить результат.
Решение задач на дроби от числа и проценты
Стоит рассмотреть это подробнее, так как вы часто будете сталкиваться с проблемами с дробями как в реальной жизни, так и в учебниках и тетрадях.
Вы можете сначала рассмотреть некоторые из этих проблем вместе, а затем попытаться решить их самостоятельно.
Некоторые из проблем тривиальны. То есть, решение для них очевидно: достаточно посмотреть на их тип и заменить в них заданное значение, чтобы получить результат.
Айсберг возвышается над водой на свою высоту ߋ (ߋ mathbf> ߋ).
Капитан судна отмечает, что вертикальная высота от воды до верхушки айсберга составляет 16 метров.
Какова общая высота айсберга?
В данном случае можно сразу сказать, что целое число — это общая высота айсберга, процент от числа — 16 (метров), а дробное значение — ⌘ (⌘ mathbf> \).
Поэтому правило гласит: чтобы получить ответ, разделите 16 на ⌘ (⌘ mathbf> \) и получите результат.
\ (⌘ mathbf = 16 \ cdot11 = 176> \) (измерение) — общая высота
Ответ: 176 (метров).
Некоторые проблемы требуют более тщательного анализа для их решения.
Магазин продал пару новой спортивной обуви специальной партией, оставив в запасе 56 пар.
Какие размеры были доступны в специальной партии?
В этом вопросе, если вы не читали условие, вы интуитивно разделите 56 на ߡ (⌘ mathbf> \) и получите ответ, но ответ будет неверным.
При ближайшем рассмотрении выясняется, что 56 пар соответствуют остальной партии, а дробь ⌘ (⌘ mathbf> \) объясняет, где произошла продажа.
Однако общее количество пар еще не известно, поэтому невозможно определить, какое число соответствует ⌘ (mathbf> \).
Однако размер баланса можно рассчитать.
Если весь лот равен 1 и ޯ(⌘ mathbf> \) был продан, то остается ޯ(⌘ mathbf> \) предмет.
Эта доля соответствует оставшимся 56 парам.
Следующие шаги аналогичны описанным в предыдущей задаче.
1) \(⌘ mathbf = \ frac> \) — оставшаяся доля от общего размера партии
2) \ mathbf = 56 \ cdot3 = 168> \) (пара) вся спортивная обувь присутствовала в партии
Ответ: 168 (пара).
Могут возникнуть проблемы с более сложными условиями, решить их все невозможно, но основные из них следующие
- не давать себя запутать
- расписать, какой части какая дробь и какое число соответствует
- понять, где данных достаточно, чтобы узнать что- то новое
- и так постепенно продвигаться к ответу
Войдя в систему или зарегистрировавшись, вы можете пройти тест и получить результат.
Числа, состоящие из целой и дробной частей, могут быть преобразованы в неправильные дроби. Умножьте целую часть на знаменатель и добавьте дробные части к произведению. Полученная сумма является числителем дроби и знаменателем дробной части.
Приглашение в мир математики
Кенгуру математические задачи, решения и ответы, виды алгебры и геометрии для всех классов, подготовка к тестам ЗНО.
Игра Немтеры: сможете ли вы решить все головоломки с цифрами из букв?
Формулы для решения задач на дроби для 5 класса
В 5 классе на уроке математики учащиеся знакомятся с дробями и пропорциями. В шестом классе проблемы повторяются, но изучаются более глубоко. Дроби и проценты продолжаются в 11 классе на внешних экзаменах (ЗНО).
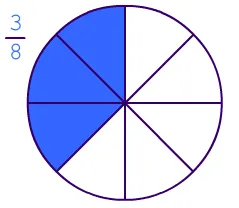
Дроби — это числа чисел, записанные в строках. Число под чертой (знаменатель) указывает на то, что делится часть целого. Число над чертой (числитель) указывает на то, что было отобрано некоторое количество этих деталей.
Таким образом, $ \ frac $ (три восьмых) означает, что множество делится на восемь частей и берутся эти три части.
Существует три категории дробных задач. Нахождение дробей от чисел, нахождение количества дробей и представление звуков слов в виде дробей.
Как найти дробь от числа
Нахождение дробей от чисел требует знания чисел и дробей, полученных от них. Все, что вам нужно, — это найти дробное значение. Рассмотрим эту проблему.
Пример 1.1. В самолете 120 пассажиров. $ \ frac $ (2/5ths) впервые летит на самолете. Сколько пассажиров летают впервые? Это вопрос о частичных дробях. Есть число; 120. Дробь: найдите $ \ frac $ равное двум пятым от 120.
Решайте задачи на определение дробей от чисел следующим образом.
Решение Задайте себе два вопроса: 1. Сколько $\frac $ (одна пятая) от 120? Для этого разделите 120 на 5 и получите 24. 2. Сколько $ \frac $ (две пятых) от 120? Умножьте полученный результат, 24, на 2. Получится 48.
Следовательно, $ \ frac $ из 120 равно 48. ОТВЕТ: 48 пассажиров летят в первый раз.
Попробуйте решить другую задачу на нахождение дроби от числа. Пример 1.2. Население города составляет 1,5 миллиона человек. В городе $\frac$ студентов. Сколько студентов в городе?
Решение 1.Чему равно $\frac $, равное 1 500 000? 1 500 000: 25 = 60 0002.Чему равен $\frac $, равный $1 500 000 000? 60 000 * 3 = 180 000
Ответ: 18 000 000.
Когда вы приобретете опыт решения подобных задач, вы сможете объединить эти два вопроса в одну операцию, используя следующее правило Чтобы найти дробь числа, умножьте число на дробь. Или же, чтобы найти дробь от числа, разделите это число на знаменатель дроби и умножьте на числитель.
Пример 1.3. Автосалон получил 14 автомобилей. В течение месяца было продано 2/7 от этого количества. Сколько автомобилей было продано?
Решение Умножить 14 на $\frac $: $ 14 \ cdot \ frac = \ frac = 2 \ cdot 2 = 4 $
Давайте теперь рассмотрим второй тип проблем.
Как найти число по дроби
В этом типе задач исходное число неизвестно. Однако значение конкретной дроби этого числа и доля этой дроби от исходного числа известны. Для удобства рассмотрим, как бы решались те же три задачи, если бы для нахождения числа нужно было использовать дроби.
Пример 2.1. В самолете есть пассажиры (мы не знаем, сколько их!).. Известно, что 48 пассажиров или $\frac $(2/5 части) от этого числа летят впервые. Поиск: сколько пассажиров в самолете?
Фундаментальное свойство дробей используется для сокращения дробей. Деление числителей и знаменателей на общий делитель, кроме единицы, называется сокращением дробей.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравните дроби с разными числителями и знаменателями.
- привести дроби к наименьшему общему знаменателю ;
- сравнить полученные дроби.

Чтобы сократить дроби с наименьшим общим знаменателем, необходимо
- найти наименьшее общее кратное ( НОК ) знаменателей дробей (оно и будет их общим знаменателем);
- разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель ;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковым знаменателем числитель второй дроби прибавляется к числителю первой (числитель первой дроби вычитается из числителя второй), оставляя тот же знаменатель. Если возможно, полученные фракции уменьшаются, а извлекается целое.
При сложении (вычитании) дробей с разными знаменателями сначала сократите дроби до наименьшего общего знаменателя, а затем сложите (вычтите) дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Будьте особенно внимательны при сложении (вычитании) дробей, содержащих смешанные числа!

Общий случай сложения (вычитания) дробей.

Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей , а затем умножают согласно п. 1.

Деление дробей
Два числа считаются обратными, если их произведение равно 1. Другими словами, дроби, такие как a/b и b/a, являются обратными. Например, 1/3 и 3. Чтобы разделить одну дробь на другую, умножьте делитель на величину, обратную делимому.

При делении чисел, состоящих из целых и дробных частей, их сначала нужно представить в виде неправильных дробей.

Нахождение части от целого (дроби от числа)
Чтобы найти доли целого, разделите числа, соответствующие множеству, на знаменатель дроби, представляющей дробь, и умножьте результат на числитель дроби.
Задача нахождения частей целого по сути является задачей нахождения частей чисел. Чтобы найти дробную часть (долю) числа, умножьте число на дробь.

Пример 3.3. автомобили, ввезенные для выставки, были проданы в течение одного месяца. Если автодилер продал в общей сложности 14 автомобилей, сколько это всего автомобилей?
Онлайн калькулятор нахождения значения дроби от числа
Теперь предоставьте активный онлайн-калькулятор. Это позволяет легко вычислить дробь числа, и наоборот, если вы знаете часть этой части и ее часть в виде числового значения.
Введите значения дроби для вычисления ее в виде части от исходного:
Найдите число, в котором дробь является частью «исходного числа».
Найдите дробное значение числа.
Находит число, часть которого представляет собой дробь, а дробь, как известно, является «исходным числом» числа.








