Как находить наибольший общий делитель (НОД) двух чисел. Как находить наибольший общий делитель

Аналогично, их можно найти и по другим ценам: 100 и 40. 100 и 40. После разложения из первого удаляются еще пять. Распространение дает 20. Это самый большой раздел после валидации.

Как находить наибольший общий делитель (НОД) двух чисел

Одна из проблемных задач современных школьников, которые привыкли пользоваться встроенными в свои устройства калькуляторами, — найти наибольшее общее делимое двух или более чисел.

Невозможно решить математическую задачу, если не знать, что представляет собой настоящий вопрос. Для этого необходимо знать выражения, используемые в математике.

Общие понятия и определения

Необходимо знать:.

1. Если некое число можно использовать для подсчёта различных предметов, например, девять столбов, шестнадцать домов, то оно является натуральным. Самым маленьким из них будет единица.
2. Когда натуральное число делится на другое натуральное число, то говорят, что меньшее число — это делитель большего.
3. Если два и более различных числа делятся на некое число без остатка, то говорят, что последнее будет их общим делителем (ОД).
4. Самый большой из ОД именуется наибольшим общим делителем (НОД).
5. В таком случае, когда у числа есть только два натуральных делителя (оно само и единичка), оно называется простым. Самое маленькое среди них — двойка, к тому же она и единственное чётное в их ряду.
6. В случае если у двух чисел максимальным общим делителем является единица, то они будут взаимно простыми.
7. Число, у которого больше чем два делителя, именуется составным.
8. Процесс когда находятся все простые множители, которые при умножении между собой дадут в произведении начальное значение в математике называют разложением на простые множители. Причём одинаковые множители в разложении могут встречаться неоднократно.

В математике принята следующая символика

Различные способы найти НОД

Самый простой способ ответить на этот вопрос — если наименьшее число является делителем многих. В этом случае он является наибольшим общим делителем.

Например, nod (15; 45) = 15, nod (48; 24) = 24.

В математике такие случаи очень редки, поэтому существуют более сложные способы поиска узлов, но перед началом работы неплохо бы проверить.

Способ разложения на простые сомножители

Если вам нужно найти два или более различных чисел, достаточно разделить каждое из них на первый множитель и выполнить процесс умножения на коэффициенты каждого числа.

Рассмотрим, как найти узлы 36 и 90:.

Теперь посмотрим, как то же самое можно найти в случае трех чисел: 162. 162; 42.

Поскольку мы уже знаем, как свернуть 36, давайте разберемся с остальным: с

Следовательно, nod (36; 162; 42) = 1*2*3 = 6.

Обратите внимание, что необязательно писать в расширениях.

Давайте посмотрим, как просто проанализировать первый фактор. Напишите искомое число в левой части и первый делитель в правой части.

Колонки могут быть разделены либо знаком деления, либо простой вертикальной линией.

1. 36 / 2 продолжим наш процесс деления;
2. 18 / 2 далее;
3. 9 / 3 и ещё раз;
4. 3 / 3 сейчас совсем элементарно;
5. 1 — результат готов.

Евклидов способ

Этот вариант известен человечеству по древнегреческой культуре, он гораздо проще и приписывается великому математику Евклиду, но подобные алгоритмы использовались и ранее. Метод заключается в делении большего числа на меньшее по следующему алгоритму Затем делитель делится с остатком делимого и так продолжается до тех пор, пока не будет разделено все число. Окончательное значение будет наибольшим общим делителем.

Следуйте примеру использования этого алгоритма.

Найдем узлы 816 и 252.

1. 816 / 252 = 3 и остаток 60. Сейчас 252 разделим на 60;
2. 252 / 60 = 4 в остатке на этот раз окажется 12. Продолжим наш круговой процесс, разделим шестьдесят на двенадцать;
3. 60 / 12 = 5. Поскольку на сей раз никакого остатка мы не получили, то у нас готов результат, двенадцать будет искомым для нас значением.

Таким образом, в конце процесса мы получили нод (816; 252) = 12.

Действия при необходимости определения НОД если задано более двух значений

Вы узнали, что делать, когда есть два разных числа. Теперь вам нужно знать, что делать, если чисел три или больше.

Несмотря на кажущуюся сложность, эта проблема не вызывает у нас никаких затруднений. Следующий шаг — выбрать два числа и определить цену, которую вы ищете. Следующий шаг — кивнуть этот результат и найти третье из заданных значений. Затем мы снова действуем в соответствии с четвертым известным авторитетом.

Как и в случае с НОД, поиск ННК может осуществляться тремя способами, аналогичными предыдущим. Каждый из них может быть использован в зависимости от состояния и легкости проблемы.

Понятие наибольшего общего делителя

Во-первых, поймите, что такое общий делитель. Существует множество делителей для целых чисел. И сейчас нас особенно интересует, как одновременно иметь дело со многими целочисленными делителями.

Делители натуральных чисел — это целые натуральные числа, на которые число делится без остатка. Если натуральное число имеет три или более делителей, оно называется комплексным числом.

Общие делители многих целых чисел — это числа, которые могут быть делителями каждого числа в сумме. Например, числа 12 и 8 имеют общие делители 4 и 1. Чтобы проверить это, напишите верные уравнения: 8 = 4 * 2 и 12 = 3 * 4.

Каждое число может делиться само на себя на 1. Поэтому каждое множество целых чисел имеет по крайней мере два общих делителя.

Наибольший общий делитель двух чисел A и B — это наибольшее число, на которое можно разделить несимметричные числа a и b. Это можно записать с помощью аббревиатуры nod. Для двух чисел можно написать: nod(a, b).

Например, для 4 и 16 кивком будет 4.

1. Зафиксируем все делители четырех: 4, 2, 1.
2. А теперь все делители шестнадцати: 16, 8, 4 и 1.
3. Выбираем общие: это 4, 2, 1. Самое большое общее число: 4. Вот и ответ.

Наибольший общий делитель трех или более чисел — это наибольшее целое число, которое одновременно делит все эти числа.

Найдем наибольший общий делитель множества целых чисел 10, 6, 44 и 18. Оно будет равно 3. Ответ можно записать так: nod(12, 6, 42, 18) = 3. Чтобы проверить точность ответа, напишите все делители и выберите наибольший из них.

Первое взаимнооднозначное число является натуральным числом и имеет только один общий делитель — 1. Их кивок — 1.

Другой пример. Вычислите узлы 28 и 64.

Распишем простые множители для каждого числа и подчеркнем одинаковые

Вы можете искать узелки в колонках, как указано выше или как показано на рисунке.

Способы нахождения наибольшего общего делителя

Существует два способа найти наибольший общий делитель. Рассмотрите оба варианта, чтобы выбрать наилучшее действие при решении проблемы.

1. Разложение на множители

Чтобы найти множество чисел, просто разделите числа на первый множитель и умножьте на общий множитель всех чисел.

Пример 1. Найдите НОД (84, 90).

Разложим числа 84 и 90 на простые множители:

Пример 2. Найдите НОД (15, 28).

Разложим 15 и 28 на простые множители:

Пример 3. Найдите узлы 24 и 18.

Разложим оба числа на простые множители:

Онлайн-курсы по математике для детей могут улучшить их оценки и помочь им подготовиться к тестам, IEP и экзаменам.

2. Алгоритм Евклида

Метод Евклида помогает находить узлы через последовательные деления. Сначала посмотрите, как он работает с двумя числами, а затем примените его к трем и более.

Алгоритм Евклида заключается в следующем: если два или более чисел делятся на минимум, то наименьшее число является наибольшим общим делителем. С помощью метода Евклида легко найти больший общий делитель, используя этот тип.

nod: тип nod(a, b) = nod(b, c), где c делится на b.

Пример 1. Найдите узлы 24 и 8.

Поскольку 24 делится на 8 и 8, общий делитель этих чисел, 8, уменьшается на 8. Этот делитель максимален, потому что 8 не может быть разделено ни на какое число, большее самого себя. Таким образом, nod(24, 8) = 8.

В других случаях для нахождения наибольшего общественного делителя двух чисел выполните следующую последовательность действий.

1. Большее число поделить на меньшее.
2. Меньшее число поделить на остаток, который получается после деления.
3. Первый остаток поделить на второй остаток.
4. Второй остаток поделить на третий и т. д.
5. Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.

Пример 2. Найдите наибольший общий делитель чисел 140 и 96.

1. 140 : 96 = 1 (остаток 44)
2. 96 : 44 = 2 (остаток 8)
3. 44 : 8 = 5 (остаток 4)
4. 8 : 4 = 2

Последний делитель равен 4 — это означает: nod(140, 96) = 4.

Пошаговое деление можно описать в столбцах.

Чтобы найти наибольший общий делитель трех или более чисел, делайте это в следующем порядке.

1. Найти наибольший общий делитель любых двух чисел из данных.
2. Найти НОД найденного делителя и третьего числа.
3. Найти НОД последнего найденного делителя и четвёртого числа и т. д.

Свойства наибольшего общего делителя

Наибольшие общие делители обладают определенными свойствами. Мы описываем их в форме теории и приводим непосредственные доказательства.

Примечание: Все свойства NOD сформулированы для положительных целых чисел и учитывают только делители больше нуля.

Свойство 1. Наибольший общий делитель A и B равен наибольшему общему делителю B и A, т.е. NOD(A, B) = NOD(B, A). Изменения в цифрах не влияют на конечный результат.

Доказывать это свойство не имеет смысла, так как оно вытекает непосредственно из определения самого узла.

Неподвижный 2. Если A делится на B, то NOD(A, B) = B, так как все общие делители A и B совпадают с множеством делителей B.

Доказательство.

Каждый общий делитель чисел A и B является делителем каждого из этих чисел, содержащих B. Поскольку A кратно B, то по свойству деления каждый делитель B также является делителем A. Каждый делитель B оказывается общим делителем A и B.

Таким образом, когда A делится на B, все делители A и B равны одному целому делителю B. Кроме того, поскольку наибольшим разбиением B является сам B, наибольший общий делитель A и B равен B, то есть NOD(A, B) = B.

В частности, если a = b, то nod(a, b) = nod(a, a) = nod(b, b) = a = b.

Доказанное свойство больших делителей можно использовать для нахождения двух чисел при делении одного на другое. В этом случае кивок равен одному из этих чисел, а второе делится.

Неподвижно 3. a = bq + c, где a, b, c и q — целые числа, тогда все общие делители чисел a и b равны всем общим делителям чисел b и c. Применимо равенство nod(a, b) = nod(b, c).

Доказательство.

Поскольку существует равенство A = BQ + C, то каждый общий делитель A и B делит C по свойству деления. По той же причине каждый общий делитель B и C делит A. Поэтому каждый общий делитель A и B совпадает с каждым общим делителем B и C.

Поэтому максимумы этих общих делителей совпадают и равенство и nod(a, b) = nod(b, c) можно считать верным.

Неподвижный 4. nod(mb) = m * nod(a, b), если m — натуральное число.

Доказательство.

Умножая каждое равенство алгоритма Евклида на m и в обе стороны, его узел (MM, MB) = MR, где R — узел (a, b). Это свойство наибольшего общего делителя используется для нахождения нода путем рассмотрения первого числа.

Свойство 5. p с общими делителями чисел a и b и nod(a:p, b:p) = nod(a, b):p. То есть, если p = nod(a, b), то nod(a:nod(a, b), b:nod(a, b)) = 1, то есть числа a:nod(a, b) и B:nod(a, b) изначально взаимно однозначны.

Для предыдущего состояния, где a = p (a:p) и b = p (b:p), и для предыдущего состояния можно написать цепочку уравнений, например, nod(a, b) = nod(p(a:p)), p(b:p)) = p * nod(a:p, b:p).

Знакомство с темой наибольшего общего делителя начинается в первом классе в теории и практически подкрепляется оценками. В этой статье вы узнали все основные определения, качества, признаки и методы кивания.

Чтобы лучше понять, как найти два числа, достаточно заменить заданную переменную на первое число, например, 12 или 9. Другими словами, наименьшие делители 12 и 9 — это те, для которых решение может быть найдено без разрыва из.

Как найти наибольший общий делитель для двух чисел

При решении математических задач в начальной школе может возникнуть необходимость найти наибольший общий делитель или кивок на аббревиатуру. Однако не все студенты знают правильный алгоритм этого закона и путают его с НОК (наименьшее общее кратное). Чтобы избежать подобных ошибок, математики разработали универсальный алгоритм для различения и нахождения цен.

При решении математических задач в начальной школе может возникнуть необходимость найти наибольший общий делитель или кивок на аббревиатуру. Однако не все студенты знают правильный алгоритм этого закона и путают его с НОК (наименьшее общее кратное). Чтобы избежать подобных ошибок, математики разработали универсальный алгоритм для различения и нахождения цен.

Общие сведения

Перед началом обучения эксперты рекомендуют написать список основных знаний, необходимых для нахождения наибольшего общего делителя и меньшего общего кратного. Он состоит из следующих элементов.

1. Определения величин.
2. Признаки делимости чисел.
3. Разложение на простые элементы или множители.
4. Алгоритмы или методики нахождения.

НОД — это максимальное значение, на которое делятся два или более чисел. NOC — это параметр, описывающий наименьший общий делитель. Чтобы понять разницу между этими терминами, необходимо проанализировать акт деления двух чисел.

Первый элемент — делитель. Это означает, что делитель делится на определенный элемент (делимое). Результатом является коэффициент. Математики называют последнее квантом двух или более величин. Затем необходимо проанализировать точки делителей.

Признаки делимости

В математике есть два понятия: числа и цифры. Основное отличие заключается в том, что комбинация цифр приводит к цифре. Кроме того, каждое значение состоит из чисел (единиц, десятков, тысяч и тысяч). Эти числа читаются слева направо. Так, 657 состоит из единиц (7), десятков (5) и сотен (6). Стоит поискать их комбинацию. Операция выглядит следующим образом: 7 + 50 + 600 = 657.

Точка деления — это критерий, с помощью которого число может быть разделено на требуемое значение без остатка. Включены следующие правила.

1. R (любое действительное число).
2. Последняя цифра — четная, т. е. 24/2 — делится, т. к. 4 — четное.
3. Сумма цифр, составляющих число, возможно разделить на 3. Пример: 36/3==12.
4. Последние 2 цифры можно разделить на 4, т. е. 844/4==211.
5. Последний разряд эквивалентен одному из двух значений (0 или 5), 810/5==162.
6. Для числа 6 одновременно выполняются второй и третий пункт. Пример: 96/6= и =16.
7. 7: расчет по формуле a*b*c*d+e/7, где e — разряд единиц, а все остальные (слева направо) — десятки, сотни, тысячи и десятки тысяч. Правило справедливо и для величин с разным количеством разрядов. Пример: 861/7==123.
8. Деление на 8 осуществляется по второму и четвертому признакам одновременно, т. е. 184/8= и =23.
9. Сумму разрядов можно разделить на 9. Пример: 108/9==12.
10. Последняя цифра эквивалентна 0, т. е. 140/10==14.
11. 2 разряда равны между собой (11, 22, 33 и т. д. ) или величина, образованная разрядами сотен и десятков без единиц, делится на 11 (121=).

Однако признаков деления недостаточно, чтобы перейти к соответствующему алгоритму. Следующим шагом является разбиение числа на простые элементы натурального типа.

Разложение на простые элементы

Основные элементы — это числа, делящиеся на единицу или один эквивалент, т.е. 7/1 и 7/7. Снизить цену ключевых элементов — найти набор чисел, произведение которых будет соответствовать искомой цене. Например, 30 = 3*5*2. математики разработали специальные алгоритмы для выполнения этого действия.

Примеры решения

Одна из трудностей заключается в следующем: найти наибольший общий делитель чисел 32, 66 и 84. Для ее решения могут быть использованы методы. Оптимальным является умножение.

Не рекомендуется решать евклидовым методом, так как это усложняет расчет. Фундаментальным принципом в физико-математических дисциплинах является оптимизация вычислений. Это означает, что вам необходимо найти метод с наименьшим количеством преобразований и вычислений.

В следующей задаче необходимо найти узлы 66, 121, 77 и 110. В этом случае также рекомендуется разделить все четыре числа на первый коэффициент. Поиск решений осуществляется с помощью этой методологии.

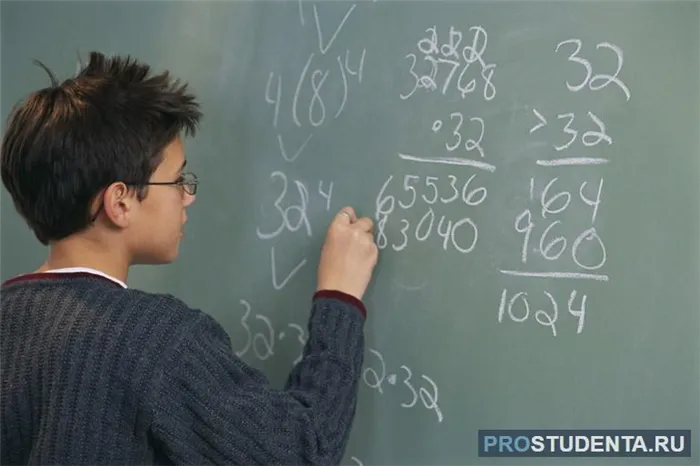
Глядя на эти два примера, можно сделать вывод, что найти кивок довольно просто. Далее необходимо найти 22 и 32 НОК. Это делается с помощью данной методологии.

Другой тип задачи — одновременное нахождение НОД и НОК для чисел 45, 85, 94 и 96. Решения могут принимать следующие формы

1. 45=5*3*3.
2. 85=17*5.
3. 94=2*47.
4. 96=2*2*3*2*2*2.
5. НОД=1 (нет общих множителей, кроме единицы).
6. НОК=5*3*3*17*2*47*2*2*2*2*2=1150560.

В математике есть и более сложные задачи. Одно из них утверждается следующим образом: два числа равны 9, первое число — 90, которое больше второго. Необходимо найти значение интеграла, наиболее близкое ко второму. Задача решается следующим алгоритмом

Поскольку ближайшее целое число равно 81, задача решается методом подбора.

Поэтому поиск ноды — очень простой процесс, если иметь базовые знания по алгоритму.