В конце XVI века Франсуа Виеру, одному из основателей современной алгебры, удалось получить свойства корней путем изучения квадратичных уравнений. Математика может быть записана следующим образом:.
Решение (корни) квадратного уравнения
Квадратное уравнение — это уравнение вида ax. + Bx + c = 0. где x — квадратичная переменная в уравнении, a, b и c — некоторые числа, a. 0.
Например, квадратное уравнение имеет вид
В квадратном уравнении ax²+bx+ c = 0 коэффициент a называется первым коэффициентом, b — вторым коэффициентом, а c — свободным членом.
Оно называется неполным квадратным уравнением.
Нахождение корней квадратного уравнения означает решение квадратного уравнения.
Уравнение b²-4ac называется квадратом уравнения и используется для вычисления корней квадратного уравнения, обозначаемого буквой D.
Корни квадратного уравнения можно использовать следующим образом.
-Анализ квадратных уравнений с множителями. Это техника упрощения уравнений (например, сокращение дробей, вынесение наименьшего общего знаменателя за скобки и т.д.). В частности, находить пределы, производные и интегралы.
-решать задачи, связанные с параметрическими отношениями переменных объектов (корни квадратного уравнения, в большинстве случаев один, как правило, является окончательным решением).
Геометрический смысл решения квадратного уравнения
График левой части квадратного уравнения, квадратной тройки ax²+bx+c, представляет собой параболу, ось симметрии которой параллельна оси 0y. Количество пересечений параболы с осью 0x определяет количество корней в квадратном уравнении. Если есть два пересечения, то квадратное уравнение имеет два действительных корня; если есть пересечения, то квадратное уравнение имеет один действительный корень; если парабола не пересекает ось 0x, то квадратное уравнение не имеет действительных корней. Приведенная ниже диаграмма иллюстрирует три вышеуказанных случая.
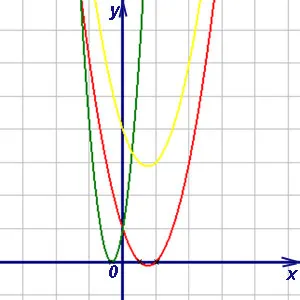
Как видно из диаграммы, красная парабола пересекает ось 0x в двух точках, зеленая парабола пересекается в одной точке, а желтая парабола не имеет пересечения с осью 0x.
Три случая после нахождения дискриминанта квадратного уравнения
1. если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.
Они рассчитываются с помощью следующего уравнения
2. если дискриминант равен нулю (), то квадратное уравнение имеет один действительный корень или два одинаковых действительных корня.
Если разрешение меньше нуля (), то квадратное уравнение не имеет действительных корней, но имеет комплексные корни, но в этой статье не обсуждается нахождение комплексных корней. В общем случае правильным решением является утверждение, что квадратное уравнение не имеет действительных корней.
Пример 1.Определите количество действительных корней квадратного уравнения.
Решение. Найдите характеристику:.
Поскольку дискриминант больше нуля, квадратное уравнение имеет два верных корня.
Дробные уравнения, в которых хотя бы одно из слагаемых имеет неизвестную дробь в знаменателе, также должны решаться путем преобразования в квадратное уравнение.. О том, как решать дробные уравнения путем преобразования их в квадратные уравнения, см.
Пример 2.Определите количество действительных корней квадратного уравнения.
Решение. Найдите характеристику:.
Поскольку дискриминант равен нулю, квадратное уравнение имеет действительные корни.
Пример 3.Определите количество действительных корней квадратного уравнения.
Решение. Найдите характеристику:.
Поскольку характеристика меньше нуля, квадратные уравнения не имеют действительных корней.
Нахождение корней квадратных уравнений необходимо для решения многих задач по высшей математике, таких как пределы, интегралы, возрастания и функции.
Целое уравнение и его степень
Мы уже изучили все представление. Это имя, данное каждому выражению в переменных, которое может использовать арифметические действия, включая умножение. Однако важным ограничением является то, что во всем представлении переменные не могут находиться в знаменателе любой дроби или быть частью делителя. Кроме того, переменная не может быть меньше знака корня. Пример интегрального выражения приведен на рисунке.
(n 3 + 7)/5 (без переменных и только с числами в знаменателе)
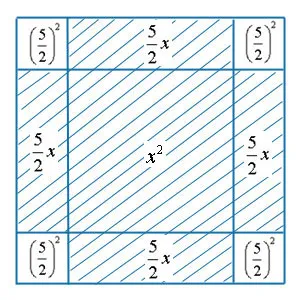
А следующее является примером непрямого выражения.
Особенностью целочисленных выражений является то, что переменные могут принимать произвольные значения. Поскольку порядок дробей ненулевой, а выражение под знаком корня неотрицательное, непрямые выражения имеют ограничения на значения переменных.
Введем понятие неповрежденных уравнений.
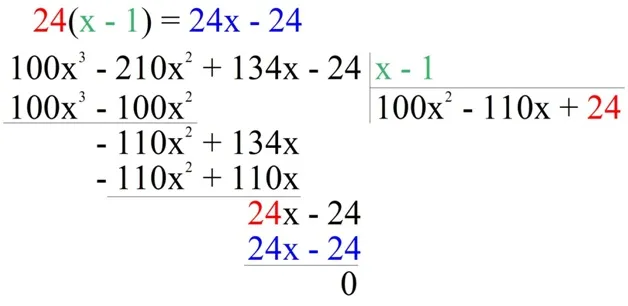
Рассмотрим пример с целым числом:.

Помните, что в математике существует понятие эквивалентного уравнения.
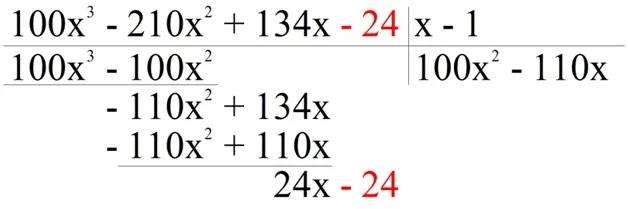
Когда вы решаете уравнение, вы записываете эквивалент предыдущего уравнения в каждой новой строке. Для этого используйте эквивалентное преобразование (перенесите сумму через точки = с противоположными знаками, разделите обе части уравнения на одно и то же число и т.д.).
Можно доказать, что мы можем преобразовать целочисленное уравнение и получить другое уравнение, содержащее многочлен в левой части и нули в правой (мы этого не делаем). Все, что нам нужно сделать, это раскрыть скобку, умножить уравнение на число и убрать дробь.
Пример. Преобразование уравнения интегрального числа.
так, чтобы левая часть была многочленом, а правая равнялась нулю.
Решение. В уравнении есть дроби 5 и 4. Если умножить обе части на 20 (наиболее частое кратное 5 и 4), то дроби исчезнут.
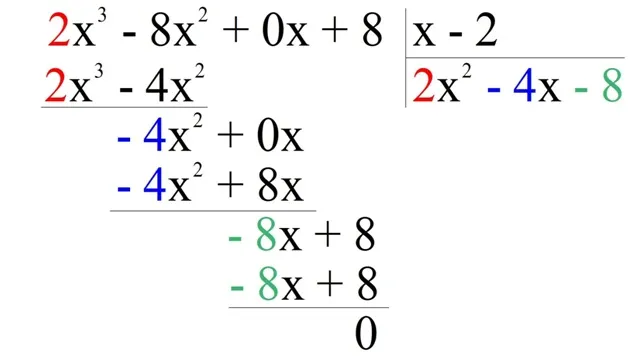
4 (5x 3-3x 4 + 45x -27x 2) — 40 = 10x 2 + 5x + 35
20x 3-12x 4 + 180x -108x 2-40 = 10x 2 + 5x + 35
Остается только сдвинуть все тоталы влево и поднять аналогичные тоталы.
20x 3-12x 4 + 180x -108x 2-40-10x 2-5x -35 = 0
-12x 4 + 20x 3-118x 2 + 175x -75 = 0
Мы получили определение в той форме, в которой должны были найти его в Конвенции.
Ответ: -12x 4 + 20x 3-118x 2 + 175x -75 = 0
В математике каждый полином можно записать как p(x). Если мы получаем уравнение многочлена, в котором одна часть является многочленом, а другая равна нулю, мы говорим, что получили уравнение вида p(x) = 0.
Видно, что решение комплексного уравнения всегда можно свести к решению уравнения p(x) = 0. Именно поэтому многочлены играют такую важную роль в математике.
Решение уравнений методом подбора корня
Нет необходимости преобразовывать уравнение, чтобы найти его корни. Один из способов решения сложных уравнений — ликвидация открытия. Если вы хотите доказать, что число является корнем уравнения, достаточно заменить его на число и получить верное равенство.
Пример. Докажите корень уравнения
x 3-2x 2 -x + 2 = 0
Это только (-1), 1 и 2.
Решение. Обменяйте каждый из возможных корней в уравнении, чтобы получить следующее уравнение. Для x = -1 мы имеем
Наконец, рассмотрим случай x = 2
Поскольку исходное уравнение в трех степенях, существует не более трех корней. То есть, нет корней, кроме (-1), 1 и 2.
Конечно, собирать корни таким образом может быть очень сложно. Однако есть несколько правил, которые могут помочь. Сначала вводится понятие коэффициентов в уравнении.
Ясно, что уравнение p(x) = 0 может быть записано в общем виде следующим образом
Числа а0, � 1, � 2,… � nКоэффициенты уравнения называются.
5x 4-7x 3 + 9x 2 -x + 12 = 0
Если одно из слагаемых «отсутствует» в уравнении, то коэффициент перед ним принимается равным нулю. Например, в уравнении
Термины в алфавите X 2 не включены. Уравнение можно считать эквивалентным символизму
Существует термин X 2, но ему предшествует ноль. В результате получается1 = 0.
Для первого фактора a0 Мы можем назвать главный коэффициент последнего фактора an — термин «свободный срок» или «свободный фактор».
Изучение коэффициентов уравнения помогает быстрее найти корень. Применима следующая теорема.

Докажите это утверждение. Пусть m — целочисленный корень уравнения, содержащего целое число
Затем мы можем заменить m в уравнении, чтобы получить правильное уравнение.
Разделите обе части на m и получите
Поскольку правая часть является целым числом (нулем), сумма чисел в левой части также является целым числом. Все номера а0m n -1, a1m n -2, an-1Они явно являются целыми числами (поскольку и m, и все коэффициенты — целые числа). Таким образом, количество интегралов дляn/m должен быть нетронутым. Однако это возможно только в том случае, если m является делителем отn .
Теорема гласит, что для отбора корней уравнения рассматриваются только те, которые являются делителями свободного члена. Необходимо также учитывать отрицательные делители.
Пример. Найдите неповрежденные корни уравнения
2x 4 -x 3-9x 2 + 4x + 4 = 0
Решение. Поскольку все коэффициенты в уравнении являются целыми числами, то целочисленный корень должен быть свободным членом, т.е. делителем 4. (-4). Заменив каждое из этих чисел в уравнении, мы получим истинное уравнение только для чисел 1, 2 и (-2).
2-1 4-1 3-9-1 2 + 4-1 + 4 = 2-1-9 + 4 + 4 = 0
2-2 4-2 3-9-2 2 + 4-2 + 4 = 32-8-36 + 8 + 4 = 0
2-(2)4-(- 2)3- 9-(- 2)2 + 4(- 2) + 4 = 32 + 8- 36- 8 + 4 = 0
Таким образом, только эти числа являются неповрежденными корнями уравнения. Поскольку мы имеем дело с уравнением с четырьмя точками, то, вероятно, существуют три целых корня и дробь.
Решение уравнений с помощью разложения многочлена на множители
Если мы можем проанализировать многочлен коэффициентов уравнения в левой части в форме p(x) = 0, мы можем приравнять каждый коэффициент в отдельности равным нулю.
Пример. Решение уравнения
Решение. Силы x 4 можно записать как (x 2)2 и 16 — 4 2. В левой части мы видим, что существует квадратичная разность, которая может быть проанализирована множителями через известные типы.
Приравнивая скобку к нулю, получаем два квадратных уравнения.
Первое уравнение имеет два противоположных корня: 2 и (-2). Второе уравнение не имеет корней.
Предположим, что кубическое уравнение имеет три корня, и вы находите один из них с корректировкой. Как найти оставшиеся корни? Здесь этот процесс известен как «разбиение многочленов на столбцы». Позвольте мне показать вам это на примере. Предположим, вам нужно решить уравнение
100×3-210×2 + 134x -24 = 0
Мы видим, что сумма всех коэффициентов в уравнении равна нулю.
Следовательно, первый корень равен 1.
Предположим, что исходное уравнение (x) = 0 имеет три корня.1, k2и к3. Затем у него есть еще одно уравнение.
Оказывается, что первый корень k1 = 1, т.е.
Давайте обозначим это символом p1(x) = 0 Другое уравнение, где единственными корнями являются k2 и к3(x) = 0. Очевидно, что корни уравнения
это числа 1, k2 и к3Поскольку его корни совпадают с корнями исходного уравнения, мы пишем
(x-1)-P1(x) = 100×3-210×2 + 134x-24
Разделите обе части на (x-1).
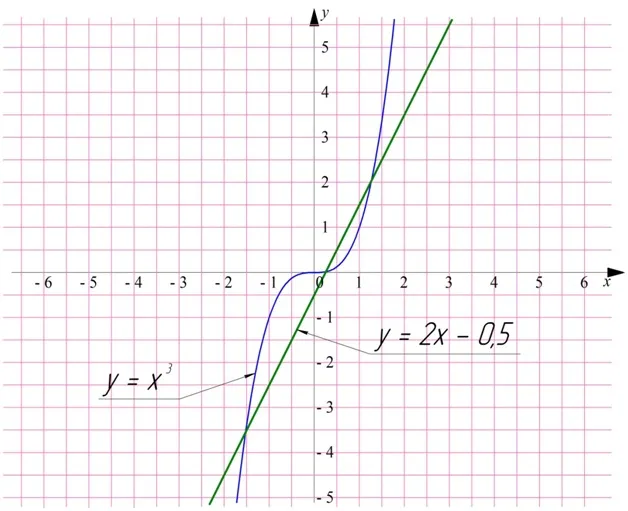
Деление исходного уравнения на x-1 дает многочлен P.1(x) и решение уравнения P1(x) = 0 являются два других корня k2и к3(x) = 0. Деление можно выполнять в столбцах. Для этого запишите первый «делитель» и «делимое», как при делении числа.
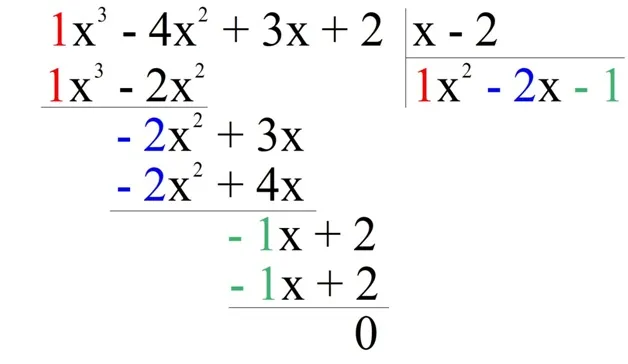
Рассмотрим первую сумму делителей. 100×3. Чтобы получить многочлен с общим числом 100×3, в каком члене нужно умножить делитель (x-1)? 100×2. Действительно, (x-1)100x 2 = 100×3-100×2. Запишите общее 100×2 как результат деления и вычтите из делителя результат умножения на делитель, то есть 100×3-100×2.
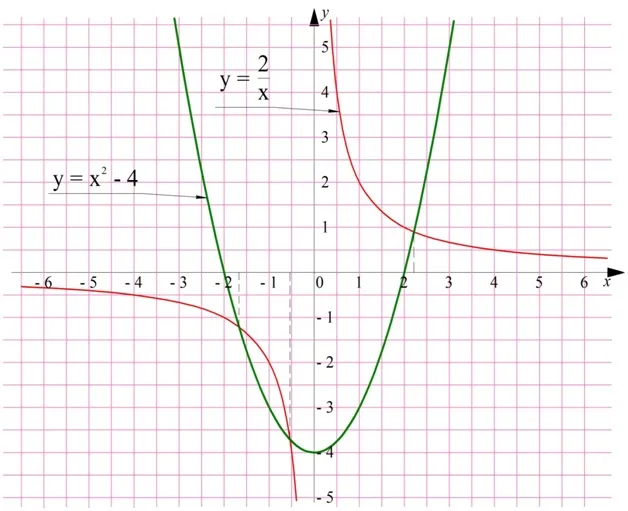

Удалите из делителя выражение, записанное под ним. Сумма 100×3, естественно, уменьшится.
(100x 3-210x 2) — (100x 3-100x 2) = 100x 3-210x 2-100x 3 + 100x 2 = —110x 2

Далее двигайтесь вниз по сумме 134x.

Чтобы получить многочлен для суммы (-110x 2), нужно умножить (x-1) на любую сумму. Очевидно, что для (-110x):.
(x-1) (-110x 2) = -110x 2 + 110x
Запишите в поле ответа сумму (-110x 2) и результат умножения на (x-1) под делимым многочленом.
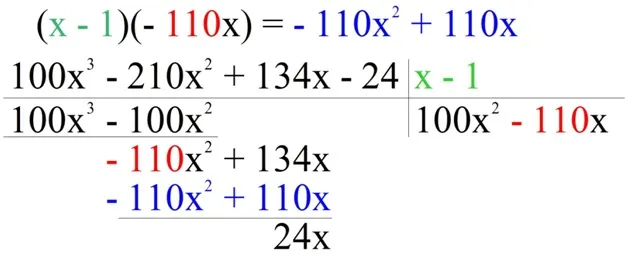
Составное уравнение имеет все необходимые корни и не имеет других корней. На самом деле, произведение множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Поэтому, чтобы решить уравнение, необходимо воспользоваться формулой
Корни квадратного уравнения
Формулы корней квадратного уравнения. Рассматриваются фактические, множественные и сложные корневые случаи. Разложение на множители квадратного триномиального уравнения. Геометрическая интерпретация. Примеры определения корня и факторизации.
Рассмотрим квадратное уравнение: (1). Корни квадратного уравнения (1) даны в виде. (2). Эти типы можно комбинировать следующим образом. Если корни квадратного уравнения известны, то квадратичный многочлен можно выразить в виде произведения коэффициентов (разложить на множители).
Далее предположим, что — является действительным числом. Изучите решение квадратного уравнения. Если разрешение положительное, то квадратное уравнение (1) имеет два различных действительных корня. Квадратичный треугольник факторов затем разрабатывается следующим образом. Если дискриминант равен нулю, то квадратное уравнение (1) имеет два кратных (одинаковых) действительных корня. Разрешение в множителях:. Если разрешение отрицательное, то квадратное уравнение (1) имеет два комплексно сопряженных корня. ? Это великолепная установка, ? Действительная и мнимая части корней следующие. ? Итак
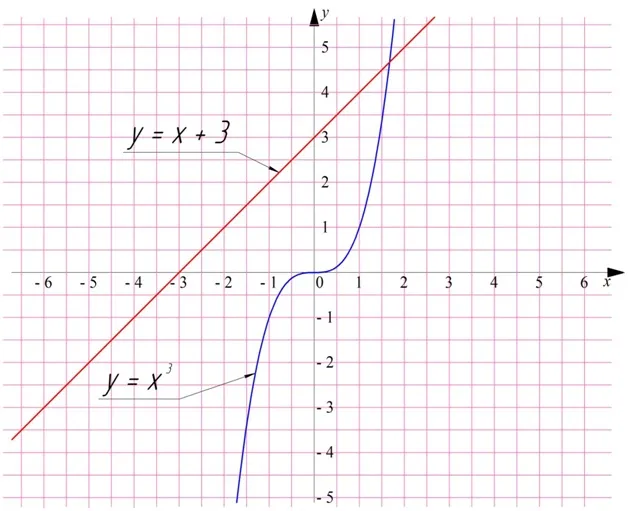
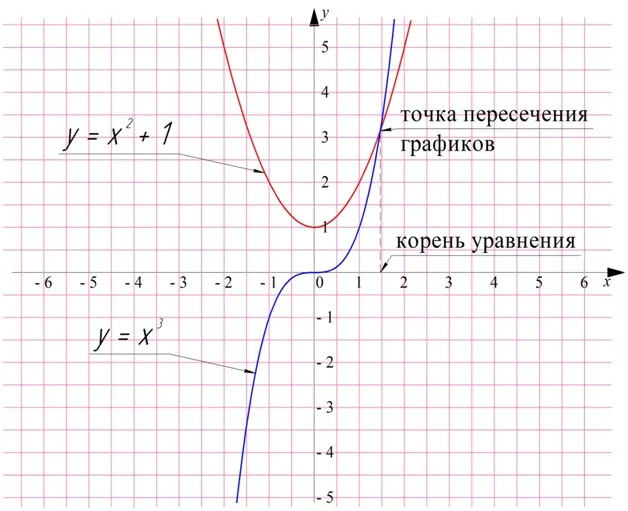
Графическая интерпретация
Если вы построите график функции, которая является параболой, то пересечение графика и оси будет корнем уравнения. В случае (1) график пересекает ось расстояний (the) в двух точках (см. рисунок ⇓). в случае, когда график пересекает ось бездны в точке (см. рис. ⇓). график не касается оси бездны (см. рис. ⇓).
Выполнение преобразований и применение уравнений (f.1) и (f.3): где? .
Таким образом, получаем квадратичное полиномиальное уравнение вида Таким образом, видно, что уравнение с Другими словами, является корнем квадратного уравнения.
Примеры определения корней квадратного уравнения
Пример 1
Найдите корни квадратного уравнения: (1.1).
Запишите квадратное уравнение в общем виде. Сравните с уравнением (1.1), значения коэффициентов следующие. Найдите характерные. Если разрешение положительное, то уравнение имеет два действительных корня. ;; .
Исходя из этого, мы определяем расширение четырехугольного триединства.
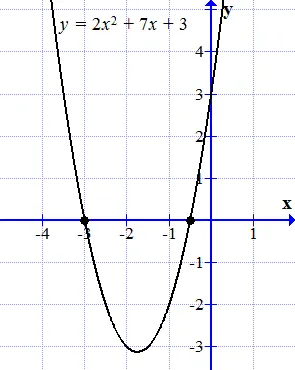
График функции y = 2 x 2 + 7 x + 3 пересекает ось расстояний в двух точках.
Графики функций. График функции — это притча. Она пересекает ось расстояния (ось) в двух точках. Эти точки являются корнями исходного уравнения (1.1).
Пример 2
Найдите корни квадратного уравнения: (2.1).
Запишите квадратное уравнение в общем виде. Сравните с исходным уравнением (2.1), чтобы найти коэффициенты. Найдите различие:. Поскольку характеристика равна нулю, уравнение имеет два кратных (одинаковых) корня. .
Три факториальных расширения аналогичны.
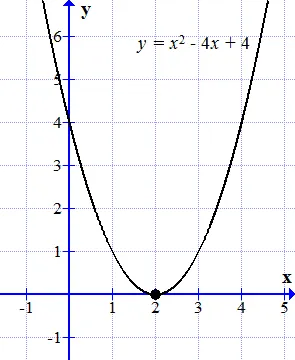
График функции y = x 2-4 x + 4 касается оси краевой линии в некоторой точке.
График функции. График функции — это притча. В определенный момент времени устанавливается вал абсцисс (вал). Эта точка является корнем исходного уравнения (2.1). Потому что этот корень входит в расширение дважды: такой корень называется множественным. Таким образом, существует два одинаковых корня.
Пример 3
Найдите корни квадратного уравнения: (3.1).
Запишите квадратное уравнение в общем виде: (1). Перепишите исходное уравнение (3.1). (Найдите факторы для сравнения с (1). Найдите различие:. Способность к занижению является отрицательной. Таким образом, фактических корней не существует.
Можете ли вы найти комплексные корни: ; ; ; ; .
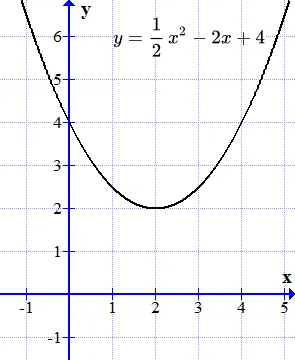
График функции не пересекает ось глубины на. Нет никаких достоверных корней.
Графики функций. График функции — это притча. Она не пересекает ось расстояния (ось). Поэтому не существует действительных корней.
Составное уравнение имеет все необходимые корни и не имеет других корней. На самом деле, произведение множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Поэтому, чтобы решить уравнение, необходимо воспользоваться формулой
Задание 4 — найдите корень уравнения log3(15-x) = log32
Это уравнение решается так же, как и экспоненциальное уравнение. Основание логарифма по обе стороны от точки «равенства» должно быть одинаковым. Поскольку это одно и то же, уравнение под знаком логарифма равносильно.
Номер 3 — это журнал.327.Чтобы было понятно, под нижним показателем логарифма находится число, поднятое силой. В нашем случае это 3. Под логарифмом число, возведенное в степень, равно 27, а логарифм — это экспонента силы. Чтобы получить 27, нужно поднять 3.
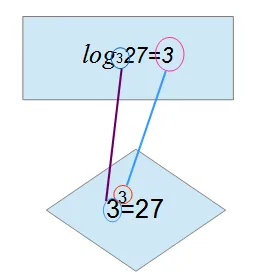
Поэтому любое число можно записать в виде логарифма. В этом случае очень удобно записать число 3 в виде логарифма, основанного на 3.
Поскольку основание логарифма равно, числа под знаком логарифма также равны.








