Второй корень (или квадратный корень) из числа, так квадратный корень из 49 равен 7, а корень третьей степени (кубический) с -7. Например, куб числа -125 равен -5.
Квадратный корень.
Квадратный корень из A (его второй корень.
— Это называется его корень.
Другими словами, квадратный корень из A — это число, которое A возводит в квадрат. Процесс получения одного квадратного корня и вычисления его значения. В большинстве случаев X и A относятся к числам, но в некоторых приложениях могут использоваться и другие математические объекты, такие как таблицы или операторы.
Пример с действительными числами: квадратные корни имеют противоположные, т.е. разные знаки (в нашем случае положительные и отрицательные числа), что усложняет работу над корнями. Для пояснения введем понятие числового корня. Цена на всегда положительная.
Свойства квадратных корней.
Помимо квадратных корней, существуют кубические корни (третьей степени), четвертые и подобные корни. Имя корня определяется номером корня.

ПРИМЕЧАНИЯ. Корни всех мощностей можно легко выразить в виде дробей.
Давайте рассмотрим, как корни связаны с дробными степенями. Существует x в степени 3/2. Запишите это выражение из точки корня. Знаменатель дробной степени подведите под корень, а числитель — под корень числа.

Только квадратный корень (корень 1 степени) не имеет чисел в корне. Это приемлемый знак.
Корень n -ной степени.
n-буквенный корень из числительного a, который, будучи поднят n-буквенной силой, производит числительное a, является числительным.
В 3, 5 и 9 классах корни — то есть все корни из ненужных чисел — приходятся на положительные и отрицательные числа.
Квадратные корни и корни четвертого, десятого и всех масштабов извлекаются только из положительных чисел.
Итак Как видите, корни записаны в виде рациональных экспонент.
Помните, что основание степени A больше нуля.
Выражение Также выполняется условие, что A больше нуля.
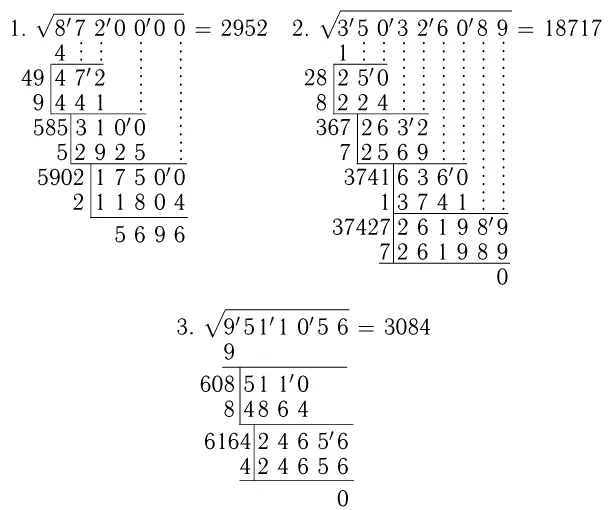
В примере 5 после удаления из первой точки квадрата 8 остаток равен нулю. Следующая грань также содержит ноль. Это показывает, что квадратный корень состоит только из 8 единиц, поэтому нам нужно заменить единицы нулями.
Ограничение корней
Первое, что нужно сделать, это выяснить, какое число является нашим корнем. Оно должно быть кратно 10:.
10 2 = 100; 20 2 = 400; 30 2 = 900; 40 2 = 1600;. 90 2 = 8100; 100 2 = 10 000.
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10000.
Что дают нам эти цифры? Просто. Они дают нам границы. Например, рассмотрим число 1296. Это число варьируется от 900 до 1600. Корень из числа может быть не меньше 30 и не больше 40.
![]()
Подпись.
То же самое относится и к другим числам, из которых можно найти квадратный корень. Пример 3364:.
![]()
Подпись.
Таким образом, вместо неоднозначного числа существует вполне определенный диапазон, в котором существует квадратный корень. Чтобы еще больше сократить поиск, перейдите ко второму шагу.
Отсев заведомо лишних чисел
Таким образом, на корень выдвинуто 10 номеров. Мы получили их очень быстро, без сложных размышлений и умножения столпов. Пришло время двигаться дальше.
Вы не поверите, но мы сократили число номинантов до двух — опять же, без сложных расчетов! Все, что вам нужно знать, — это специальные правила. Вот они.
Последняя цифра квадрата зависит только от последней цифры исходного числа.
Другими словами, достаточно посмотреть на последнее число квадрата, и вы сразу поймете, где заканчивается исходное число.
Есть только десять чисел, которые можно найти в последней позиции. Попробуйте выяснить, во что они превращаются, когда их возводят в квадрат. Посмотрите на таблицу:.
Эта таблица является еще одним шагом в расчете маршрута. Как вы можете видеть, второй ряд симметричен и состоит из пяти чисел. Например:.
Как видите, последнее число в обоих случаях одинаково. Это означает, например, что маршрут из 3364 обязательно заканчивается на 2 или 8. С другой стороны, помните об ограничениях из предыдущего пункта. Мы принимаем:.
Подпись.
Красный квадрат означает, что этот номер еще не известен. Однако маршрут находится в районе 50-60, что означает, что только два номера заканчиваются на 2 и 8.
Подпись.
Вот этот! Из всех наших возможных корней осталось только два варианта! Это самый сложный случай, так как последняя цифра может быть 5 или 0. Таким образом, у нас остается только один корень-кандидат.
Финальные вычисления
Таким образом, существует два номера-кандидата. Откуда вы знаете, что такое маршрут? Ответ очевиден: возведите оба числа в квадрат. Квадрат исходного числа является корнем.
Например, мы нашли двух кандидатов с номером 3364: 52 и 58. Пусть они будут размещены на площади.
52 2 = (50 +2)2 = 2500 + 2-50-2 + 4 = 2704; 58 2 = (60-2)2 = 3600-2-60-2 + 4 = 3364.
Это! Результат — 58! Для упрощения расчетов использовалась разница между видом суммы и квадрата. Таким образом, нам даже не пришлось перемножать номера столбцов! Это еще один уровень оптимизации расчета, но, конечно, совсем не обязательный:)
Недостатком этого метода является то, что если экспортируемый корень не является целым числом, то можно найти только это целое число, но менее точно. В то же время этот метод очень доступен для детей, решающих базовые математические задачи, требующие экспорта квадратных корней.
Приведение корней с разными показателями
Чтобы упростить формулу с корнями, содержащими корни разной силы, необходимо все корни привести к одной и той же силе.
Для этого используется следующее свойство дроби: a=n√an.
Например, существуют квадратные корни (2-я степень √2) и кубы (3-я степень √3). Во-первых, необходимо найти наименьшее общее кратное (LCC) силы. В данном примере noc = 6 (2×3). Далее применим свойство a =n√an: √2 = 2√2 = 6√23 = 6√8. 3√3 = 6√32 = 6√9Здесь два корня одной степени, и можно выполнить различные математические действия.
Корень: с ложение и вычитание корней
Основное правило для сложения и удаления квадратных корней: квадратные корни можно складывать и удалять только в том случае, если подстановки одинаковы.
Пример: 2√3+3√3 = 5√32√3+2√4 недействителен.
Чтобы сказать, следует подумать об упрощении формулы. Например: 2√3 +3√12=2√3 + 3 + 2x2x3 =2√3 + 3 + 2 x3 =2√3 +6√3=8√3.
Алгоритм действий: 1. Упростите квадратичную формулу, проанализировав ее по первому множителю. 2.Далее извлеките корень из квадратного числа и запишите полученное значение перед символом корня. 3.После процесса упрощения следует выделить корни с одинаковыми подсигналами — только их можно добавлять и удалять. 4.Корни с одинаковыми выражениями подкорней должны быть добавлены или удалены. Выражения с субститутами остаются без изменений. Не добавляйте и не удаляйте секретные номера!
Корень: умножение
Умножение корней без множителей
Произведение корней из числа равно корню из произведения этих чисел. √a *b =√a *√b Важно: перемножать можно только корни одной степени. Другими словами, вы можете умножить квадратный корень на другой корень, но вы не можете умножить квадратный корень на корень из куба. Пример: √2x√3 = √6√6x√3 = √18 = √3x 3 x 2 =3√2
Умножение корней с множителями
При умножении корней на множитель, множитель слагаемого и уравнения (числа) должны умножаться отдельно. Номера компартментов можно умножать друг на друга только в том случае, если они имеют одинаковую степень (см. размножение корней без множителя). Если множитель отсутствует, он равен единице. Пример. 3√2x√5= (3×1) √(2*5) = 3√104√2×3√3= (3×4) √(2×3) = 12√6
Корень из большого числа отрицательных чисел обычно называют фантастическим числом, а другие числа — действительными или реальными.
Метод Герона
Если вы хотите хотя бы приблизительно определить, чему равны экспортируемые маршруты (при отсутствии нетронутых цен)? Быстрые и достаточно точные результаты получаются при использовании метода Герона. Его суть заключается в использовании приблизительных типов.
Здесь r — число, для которого нужно вычислить корень; a — ближайшее число, для которого известно значение корня.
Рассмотрите, как метод работает на практике, и оцените, насколько он точен. Вычислите, чему равно √111. Ближайшее к 111 число с известным значением корня — 121. Следовательно, r = 111, a = 121. отрегулируйте значение по типу.
√111 = √121 + (111-121) / 2

Теперь проверьте точность метода.
Метод для этого метода составил приблизительно 0,3. Если вам необходимо повысить точность метода, вы можете повторить процедуру, описанную ранее.
√111=√11,3025 + (111-111,3025) /2√11,3025= 10.55-0.3025 /21.1≈10.536.
Проверьте точность расчета.
После повторного применения типа ошибки незначительны.
Вычисление корня делением в столбик
Этот метод нахождения значения квадратного корня немного сложнее предыдущего. Однако без калькулятора он является самым точным из всех других методов расчета.
Предположим, вам нужно найти квадратный корень с точностью до четырех десятичных цифр. Рассмотрим пример для произвольного числа 1308.1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
- Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
Результат √1308,1912≈36,1689. Проверяя действие в калькуляторе, можно увидеть, что все точки были определены правильно.

Поразрядное вычисление значения квадратного корня
Этот метод отличается высокой точностью. Более того, он очень понятен и не требует запоминания типов или сложных алгоритмов. Это связано с тем, что данный метод направлен на поиск правильного эффекта.
Исключите корень из числа 781. Подробно изучите последовательность задач.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
- Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Если d не требуется, d = 2 n + 1, то > \ cdot 10^. > «width =» «height =» » />. \ amptx 6 \ cdot 10^. > «width =» «height =» » />
Квадратный корень
Квадратный корень — что это такое и как найти квадратный корень из определенного числа. Это связано с тем, что квадратные корни отличаются от умножения и подобия. Давайте разберемся в сути проблемы.
Квадратный корень из числа A — это положительное число b, а его квадрат — число A. Символы для квадратного корня следующие. ‘квадратный корень из числа’ и ‘экспорт квадратного корня’. Итак, если
, тогда .
.
Устранение двузначности — введение арифметического корня
Чтобы устранить двойственность квадратного корня и двойственность степенного корня, вводится понятие числового корня.
Арифметический корень из степени числа — это неотрицательное число с равными степенями и является натуральным числом.
Пример: и.
На школьных уроках рассматривается только числовое значение корня. Другими словами, это не только имеет смысл, но вы получаете только неотрицательные значения.








