Измерения прямоугольного параллелепипеда и его свойства. Сколько у параллелепипеда ребер

Следует отметить, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется как совместно с другими обучающимися, так и в отдельных классах или группах.

Измерения прямоугольного параллелепипеда и его свойства

Параллельные релепидалы — это шестигранные призмы, в которых расположены прямоугольники.

Согласно другому определению, это многогранник, состоящий из шести граней параллельных линий.

Математика в целом, и геометрия в частности, имеет несколько основных типов подобия.

Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до выкидыша). Если вы не можете написать работу самостоятельно, закажите ее здесь.

• прямоугольный;
• прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
• наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
• ромбоэдр — шестигранная призма, грани которой — это ромбы;
• куб — состоит из квадратных граней.

Прямоугольник — это шестиугольная призма, стороны которой, как правило, прямоугольные. Это также многогранник, основание которого прямоугольное, а стороны перпендикулярны основанию.

В окружающем нас мире существует множество прямоугольных аналогов. К ним относятся комнаты, закрытые книги, коробки компьютерных систем, закрытые подарочные коробки и спичечные коробки.

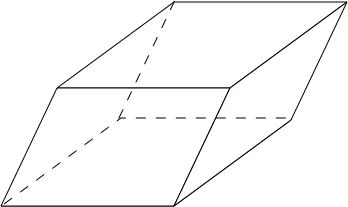
Как и все остальное, прямоугольные прямоугольники состоят из

• основания;
• граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
• ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
• диагоналей — отрезков, соединяющих противоположные вершины;
• диагоналей граней;
• высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах требуется найти число компонентов шестиугольной призмы. Эти числа можно запомнить; трехмерная форма состоит из восьми вершин, 12 граней и шести поверхностей.

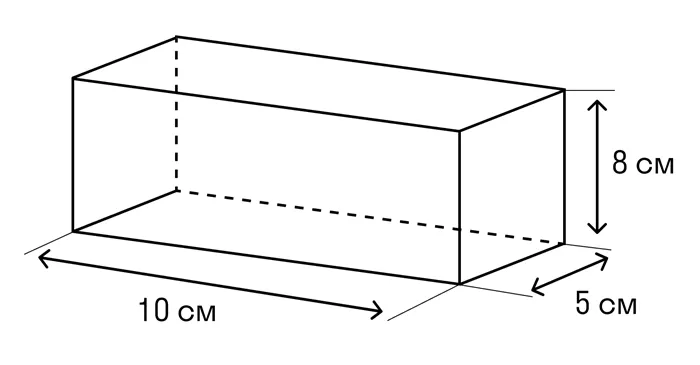
Измерениями прямоугольной параллели являются ее длина, ширина и высота.

Свойства параллелепипеда, какими обладают противолежащие грани

Независимо от типа параллели, все они обладают четырьмя свойствами.

1. Противолежащие грани равны друг другу и попарно параллельны.
2. Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
3. Фигура симметрична относительно середины диагонали.
4. Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольные параллели обладают всеми этими качествами и особыми свойствами.

1. Все стороны — прямоугольники.
2. Все углы, состоящие из двух граней, равны 90°.
3. Любую сторону можно принять за основание.
4. Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Как найти диагональ и ширину прямоугольного параллелепипеда

Согласно одному из основных свойств параллели, диагональный квадрат равен сумме трехмерных квадратов. Давайте запишем это как тип:.

Поэтому длина диагонали равна квадратному корню из суммы трехмерных квадратов на диаграмме.

Длина, ширина и высота обычно рассчитываются как объемные типы.

Существует также второй способ, с помощью которого можно найти одно из измерений. Если известны смежные размеры и диагонали общей стороны шестиугольника, то вторая сторона может быть вычислена по теореме Пифагора или свойству диагоналей.

В окружающем нас мире существует множество прямоугольных аналогов. К ним относятся комнаты, закрытые книги, коробки компьютерных систем, закрытые подарочные коробки и спичечные коробки.

Содержание

Существует несколько типов параллелей:.

— это параллелепипед, у которого все грани прямоугольники;
• Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники;
• Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основания — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.

Основные элементы

Две параллельно расположенные поверхности без общих углов называются противоположными поверхностями; поверхности с общими углами называются смежными поверхностями. Две вершины параллельных уровней, которые не принадлежат одному и тому же акну, называются противоположными. Отрезки, соединяющие противоположные вершины, называются параллельными диагоналями. Длины трех ребер прямоугольного параллельного уровня с общей вершиной называются его размерами.

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы

Прямой параллелепипед

Площадь стороны s_warr.=рр _� *H, где p _� — Периметр основания, H — высота

Общая поверхность s_п= s_warr.+2s _� где s _� — Базовая площадь

Прямоугольный параллелепипед

Площадь стороны s_warr.= 2c(a+b), где a и b — стороны основания, а c — прямоугольник

Общая поверхность s_п= 2(ab+bc+ac)

Объем v = ABC, где a, b и c — размеры прямоугольных параллелей

Площадь стороны s_warr.= 4a², где a — пимпочка куба.

Общая поверхность s_п=6a²

Произвольный параллелепипед

Очертания и отношения наклонных параллелей часто определяются с помощью векторной алгебры. Объем параллельного уровня определяется тремя сторонами параллели и равен абсолютному значению смешанного произведения трех векторов, полученных из вершины одного. Причина между длинами сторон параллели и углами между ними дает утверждение, что грамм-идентификация этих трех векторов равна квадрату смешанного произведения 1:215.

В окружающем нас мире существует множество прямоугольных аналогов. К ним относятся комнаты, закрытые книги, коробки компьютерных систем, закрытые подарочные коробки и спичечные коробки.

Что такое параллелепипед: определение, элементы, виды, свойства

В данной публикации рассматриваются определения, элементы, виды и основные свойства параллелей, включающих прямоугольники. Представленная информация сопровождается описательными изображениями для лучшего восприятия.

Параллельные релевантности — это геометрия Вселенной. Его поверхность представляет собой прямоугольный шестиугольник. Он имеет 12 граней и шесть поверхностей.

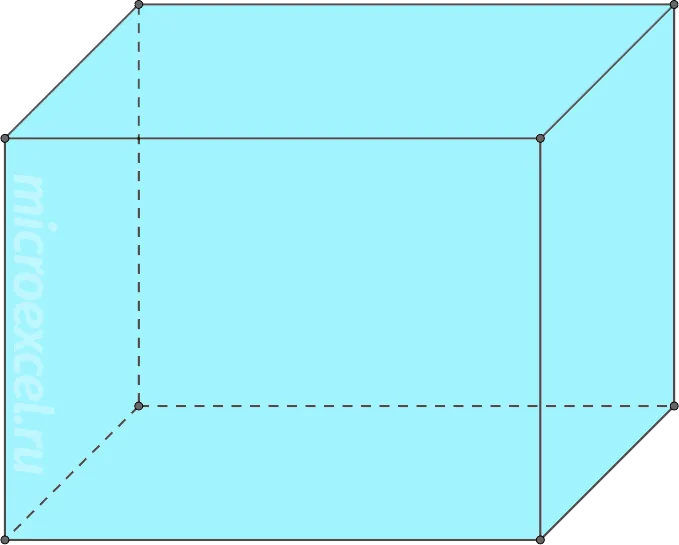
Параллельный релипидаль — это разновидность призмы, основанной на прямоугольнике. Основные элементы формы те же, что и элементы точки зрения.

Примечание: Тип расчета поверхности (для прямоугольных форм) и объем параллели могут быть показаны в отдельных публикациях.

Виды параллелепипедов

1. противоположные стороны параллели взаимно параллельны и равны параллелограмма.

2.Все диагонали параллельного полотна пересекаются в какой-то точке и разделяются в середине.

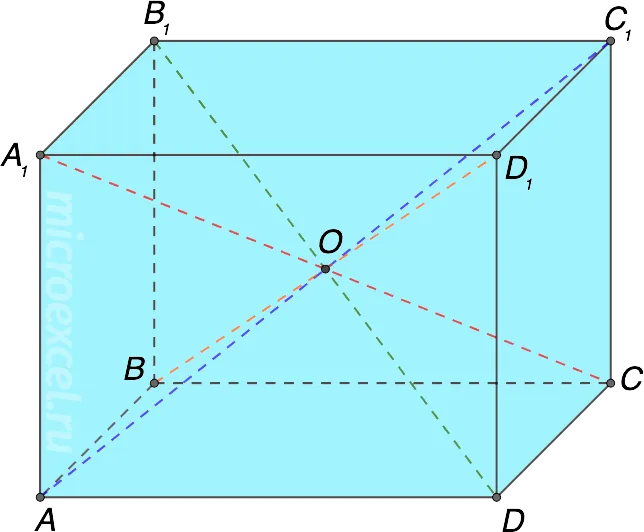
3. площадь прямоугольника с параллельными диагоналями (d) равна сумме площадей квадратов длины (a), ширины (b) и высоты (c) в трех измерениях.

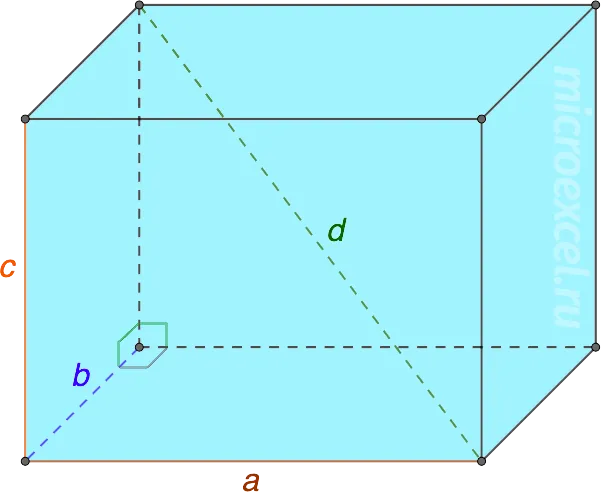
d 2 = a 2 + b 2 + c 2

Примечание: Свойство призмы также применимо к параллельным сваям.

Задача 4: Край параллельного уровня равен 10 см, а прямоугольный KLNM с размерами 5 и 7 см является частью фигуры, параллельной пупырышку. Необходимо определить внешнюю поверхность призмы.

Прямоугольный параллелепипед

Определение прямоугольной параллели:.

Прямоугольный прямоугольник — это параллельный лелепидаль, основание которого прямоугольное, а боковые грани перпендикулярны основанию.

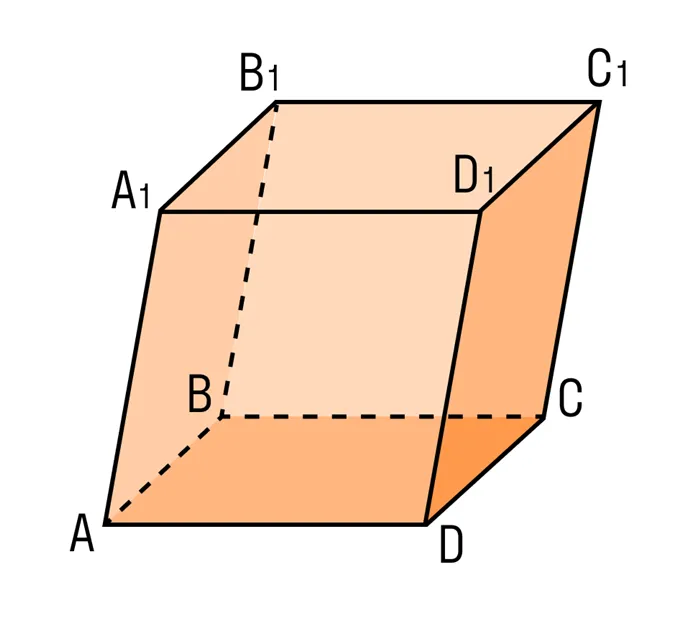
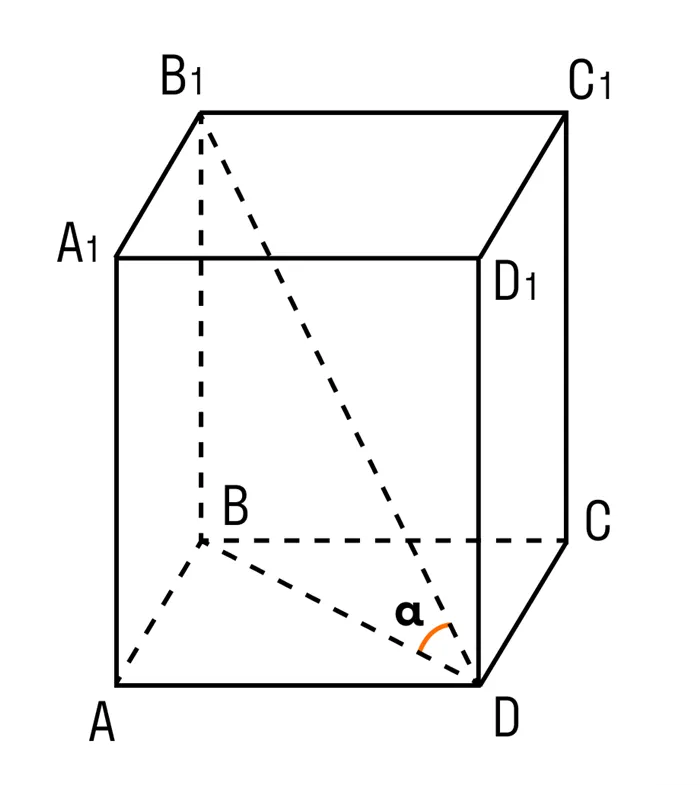
На рисунке прямоугольный прямоугольник со стороной abcd- aa1 перпендикулярен к углу abcd = 90°.

Внимательно посмотрите, как выглядит прямоугольник. Обратите внимание на разницу в прямых линиях.

Свойства прямоугольного параллелепипеда

Прямоугольные прямоугольники обладают всеми характеристиками любой параллели.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Виды прямоугольных прямоугольников:.

• Объем прямоугольного параллелепипеда V = a · b · h a — длина, b — ширина, h — высота
• Площадь боковой поверхности Sбок = Pосн·c=2(a+b)·c Pосн — периметр основания, с — боковое ребро
• Площадь поверхности Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Недостаточно знать только свойства прямоугольных параллелей, нужно уметь их доказывать.

Если существует теорема, мы должны быть в состоянии доказать ее. (в) Пифагор.

Теорема: квадраты диагоналей прямоугольной параллели равны сумме квадратов трех ее измерений.

В этом случае тремя измерениями являются длина, ширина и высота. Длина, ширина и высота — это длины трех ребер, начиная от вершины прямоугольной параллели.

Дана прямоугольная параллель ABCDA₁b₁c₁d₁. Доказательство теоремы.

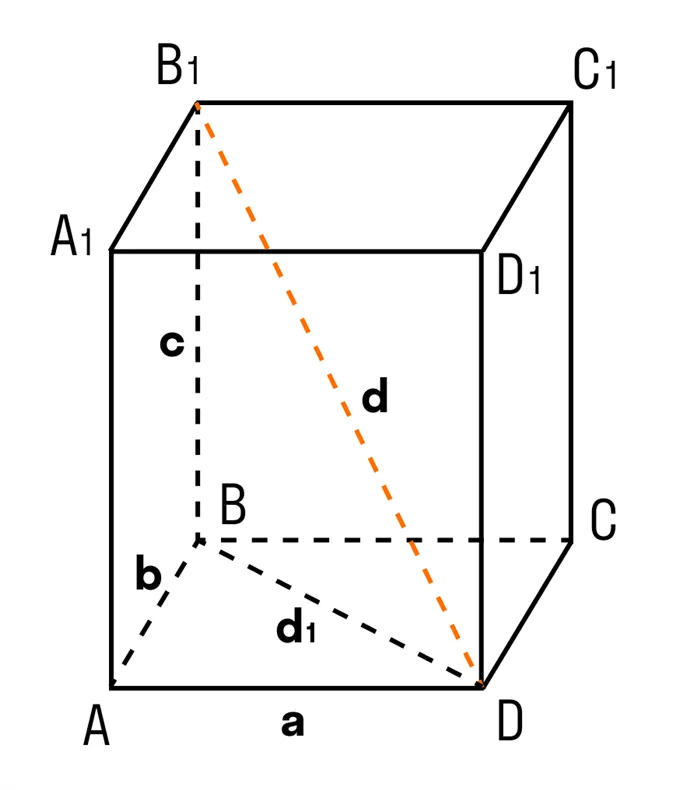
Доказательство теоремы:.

Чтобы найти диагонали прямоугольной параллели, помните, что диагонали — это отрезки, соединяющие противоположные вершины.

Все поверхности прямоугольной параллели являются прямоугольными.

DABD: по теореме Пифагора, am bad = 90°.

db₁bd: согласно теореме пифагора, amb₁bd = 90°.

Доказываемая теорема — теорема о пифагорейском пространстве.

Из определенного слова (параллельных знаков) образуйте как можно больше новых слов, состоящих из букв этого слова (причем каждая буква нового слова может быть использована один раз).

Параллелепипед — определение, свойства и измерение фигуры

Palacepipe означает параллельный уровень — призматический, а его свернутая оболочка — прямоугольная (многогранник с шестью гранями). Предметы похожей формы можно встретить в жизни и в быту. В математическом анализе и геометрии параметры одной фигуры рассчитываются по формуле.

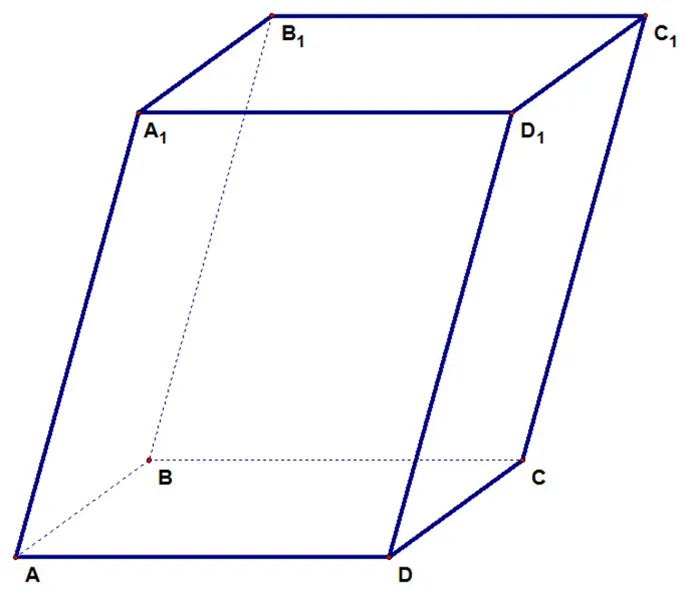
Чтобы вычислить объем, высоту и другие свойства фигуры, необходимо знать теоретическую базу и тип. Решение задач является частью единого государственного экзамена и входным билетом в университет.

Доказательство теорем

Теоретически, S на стороне PP равно S b. p. = 2(a+b)c. S полной поверхности равна S ПП = 2(AB+AC+BC).

Объем PP равен произведению трех сторон, исходящих из одной вершины (3D pp): ABC.

Доказательство: боковые грани PP перпендикулярны основанию и поэтому также имеют высоту -H = aa1 = c. Если основание прямоугольное, то SOSN =ab⋅ad= ab. Диагональ D FP можно найти по формуле D2 = A2+B2+C2. где A, B и C — измерения ФП.

Если основание прямоугольное, то △ABD — прямоугольник, по теореме Пифагора bd2 = ab2+ad2 = a2+b2. Если все стороны перпендикулярны базовой линии, то BB1⊥ (ABC) => BB1⊥BD.

Если bb1d — прямоугольник, то по теореме Пифагора B1D = BB12+BD2.

Решение задач

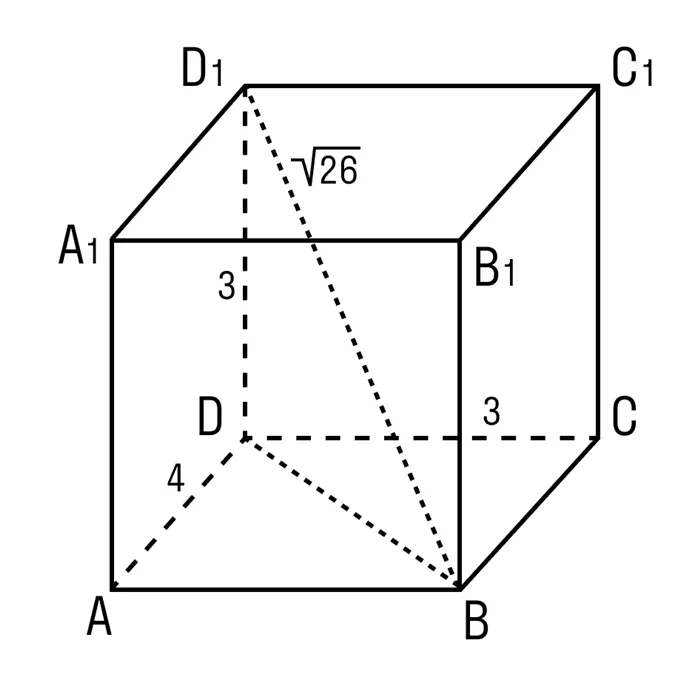
Вопрос 1: Известен ППС: нужно найти длины главных диагоналей 3, 4 и 12 см, рисунок.

Поиск ответа на вопрос начинается с построения схематического изображения, размеры которого обозначены. Используется тип B1D2 = AB2 + AD2 + AA12. После вычисления получаем выражения b2 = 169 и b = 13.

Задача 2: Начиная с общей точки, ребра PP равны 3 и 4, а общее S равно 94. Найдите третье ребро, исходящее из той же вершины.

Края символизируются A1 и A2, неизвестное — A3. Поверхность представлена соотношением: s = 2 (a1a2 + a1a3 + a2a3).

Тогда существует A3 (A1 + A2) = S/2 — A1A2. Неизвестные прыщи: A3 = S/2 -A1A2/A1 + A2 = 47-12/7 = 5.

Задача 3: Два параллельных ребра прямоугольника, исходящих из общей точки, равны 72 и 18, а диагональ равна 78. Необходимо определить объем фигуры.

Для решения задачи найдена диагональ в виде вычисления квадратного корня из суммы (a2 + b2 + c2). Здесь a, b и c — ребра. 78 является корнем из суммы 722 + 182 + C2. Решение.

ОТВЕТ: объем равен 576.

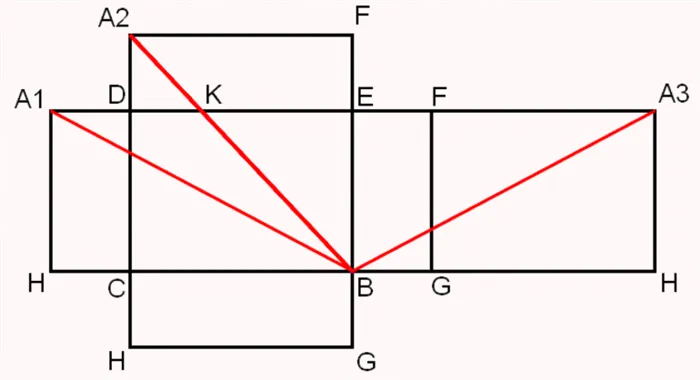
Задача 4: Край параллельного уровня равен 10 см, а прямоугольный KLNM с размерами 5 и 7 см является частью фигуры, параллельной пупырышку. Необходимо определить внешнюю поверхность призмы.

KL и AD не равны парам ML и DC. Сторона фигуры соответствует s участка пересечения, умноженному на AA1, так как пупырышки перпендикулярны участку пересечения. Ответ: 240 см².

Вопрос 5: ABCDA1B1C1D1 = 3, 4 см, внешний край равен 12 см. Необходимо определить диагонали ПП.

В основании лежат прямоугольники AB 3 см и AD 4 см. Боковые края составляют 3 см. ВВ1 — высота ПП, 12 см. Диагональ B1D2 = AB2 +BB1 2 += 9 +16 +144 =169. b1d= 13 см.

Вопрос 6: Основание ПП квадратное, а одна из его верхних вершин равна всем его нижним вершинам. Если диагональ основания равна 8 см, а внешний пупырышек — 5 см, найдите высоту фигуры.

Если основание прямоугольное, то △ABD — прямоугольник, по теореме Пифагора bd2 = ab2+ad2 = a2+b2. Если все стороны перпендикулярны базовой линии, то BB1⊥ (ABC) => BB1⊥BD.

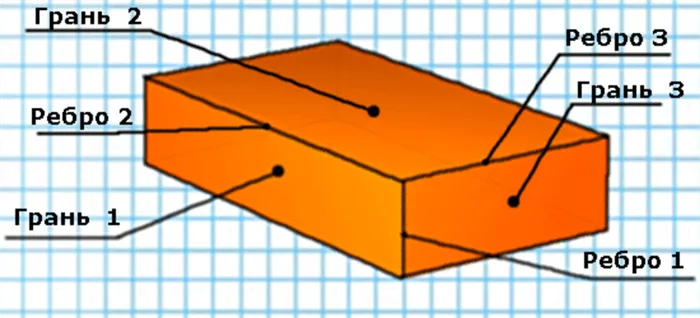
Развертки прямоугольного параллелепипеда

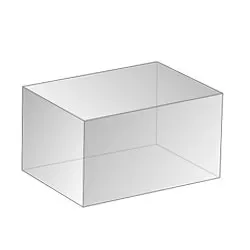
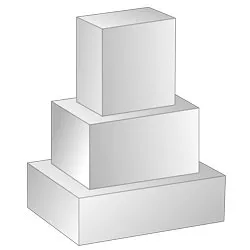
Развертки наклонного параллелепипеда

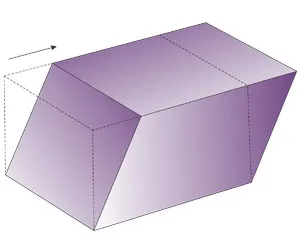
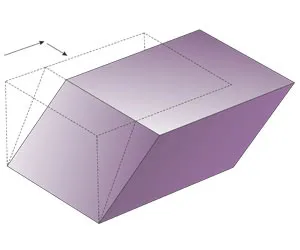
Сложности запоминания

Термин прямоугольник иногда путают с термином прямоугольник. И действительно, слова совпадают.

Прямоугольник — это четырехугольник, противоположные стороны которого параллельны, т.е. лежат на параллельных прямых. Частными случаями прямоугольников являются прямоугольники, квадраты и ромбы.

Прямоугольники — это плоские фигуры. Параллелограмм — это трехмерное тело, все стороны которого являются параллелограммами. Параллелограмм — это многогранник с шестью сторонами, каждая из которых является прямоугольником.

Интересно: «Иногда невнимательные ученики пытаются посчитать, сколько граммов в прямоугольнике и сколько параллельных труб в параллелограмме!».