Это определение Энгельса11, но Колмогаров продолжает объяснять, что все используемые термины должны пониматься в самом широком и абстрактном смысле.
Прикладная или фундаментальная: какой считают в мире математику
Как писал советский математик Колмогаров в «Службе естественных наук», остается открытым вопрос, можно ли считать математику фундаментальной наукой, является ли она простым инструментом или нет. Даже сами математики отказываются ответить на этот вопрос однозначно. Дмитрий Бебчук, математический методолог Университета Иннополис, выступил на Фестивале науки и технологий «Просто», организованном Российским университетом информатики, с докладом о том, почему без математики изобретения человека были бы невозможны, а математика не достигла бы своих практических целей.
Читайте «Хайтек» в
Наука о структурах или просто расчеты?
Математика, говорит Britannica, — это наука о структуре, классах и отношениях, благодаря своей фундаментальной практике счета, измерения и описания форм объектов. Он основан на логическом мышлении и количественных расчетах. Французская математическая группа под общим прозвищем Николя Бурбаки в 1935 году предложила следующее определение Математика — это наука об отношениях между объектами, известными не иначе, как по их свойствам. Это может привести к двойственному впечатлению. С одной стороны, существует конструктивное определение математики. ‘взять что-то и сделать это важным’. Эта своеобразная оппозиция выразилась, в частности, в создании теории множеств. Существует конструктивный подход к теории множеств, генерала Сернера Френкеля, но есть и альтернатива. За странность этого возник Рассел.
Парадокс Рассела — теоретический парадокс (антиномия), открытый Бертраном Расселом в 1901 году и демонстрирующий противоречивость рациональной системы Фреда.
Этот парадокс можно объяснить следующим образом. Назовите «обычный» набор, если он не является самим предметом. Например, множество всех людей является «нормальным». Это происходит потому, что весь набор не является человеком. Примером «необычного» множества является множество всех множеств, поскольку они являются одним и тем же множеством и, следовательно, уникальными элементами.
Вклад Цермело-Френкеля (ZF) является наиболее широко используемой версией ансамблевого офицера. Сформулированная Эрнстом Чермело в 1908 году, она преодолела парадоксы теории множеств и была усовершенствована Абрахамом Френкелем в 1921 году. Офисная система написана на языке первоклассной логики.
Он пытается доказать вам, что математика является фундаментальной наукой. Фундаментальная наука требует следующих качеств Его результаты должны быть универсальными. Она не должна иметь практического применения, заложенного в ее результатах. И это должно позволить вам приобрести новые знания о природе, т.е. прогностические навыки.
Универсальность математических результатов не вызывает сомнений. Это самый простой пункт, поэтому он стоит на первом месте. Действительно, даже на уровне «2 x 2 — 4», на каждом континенте всегда и непременно будет четверо.
Как из чистых идей родились практические инструменты
Существует четыре области математики, которые развились из совершенно абстрактных идей. Во-первых, анализ бесконечности, который сейчас называется математическим анализом. Все началось с закона об исчерпании Антифона в 5 веке до н.э. Сегодня он по-прежнему называется так. Этот метод можно использовать для нахождения областей фигур, границы которых не являются сегментами. Например, площадь круга. Если есть круг, он может быть окружен, например, пятиугольником или пятиугольник может быть окружен кругом. Площадь круга находится где-то посередине. Замена пятиугольника шестиугольником, семиугольником или восьмиугольником повышает точность подхода. Чем большее количество сторон многоугольника вписано и описано вокруг окружности, тем лучше подход.
Однако площадь круга пропорциональна квадрату его радиуса, а коэффициент пропорциональности — это число. Были предложены оценки этого числа. Архимед, например, предположил, что она равна приблизительно 22/7. Это оценка с точностью до двух знаков после запятой. А небезызвестный Цзы Чуньчжи уже предложил гораздо лучшую оценку: 355/ 113, уже с шестью знаками после запятой. Более того, оказывается, что π — иррациональное число и даже трансцендентное. Другими словами, это не алгебраическое число.
Цзу Чуньчжи был китайским математиком и астрономом. Будучи астрономом, он точно определил железные циклы планет нашей Солнечной системы. Он создал новый дневник, чтобы учесть феномен миграции. Как математик, он первым в мире вычислил пи с точностью до седьмого знака после запятой, получив значение между 3,1415926 и 3,1415927. Более точные значения были достигнуты только через тысячу лет.
Принцип Кавальери очень прост. Если есть два объемных тела одинаковой высоты и площадь разреза одинакова на каждом уровне, то объемы этих тел одинаковы. Этот принцип подходит для нахождения объемов тел, поверхности которых не обязательно плоские. Например, конусы. Исходя из этого чисто теоретического подхода, дифференциальное и интегральное исчисление возникло уже в XVII веке благодаря Ньютону и Лейбницу, двум ученым, которые развивали эту область почти одновременно. Практические приложения их работы сегодня: нахождение длин, отклонений и поворотов кривых и касательных к сферам, а также нормальных распределений в двух измерениях, позволяют искать возможные сложные события.
Бонавентура Кавальери был итальянским математиком, пионером математического анализа и самым выдающимся и влиятельным представителем «несводимой геометрии». Разработанные им принципы и методы позволили успешно решать многие аналитические задачи еще до открытия математического анализа.
В 16 веке Джероламо Кардано ввел понятие комплексных чисел. В его трудах комплексные числа описываются как совершенно сложные и бесполезные структуры, которые мы понимаем, потому что сложность — это положительная черта, а бесполезность — нет. Он абсолютно ничего не видел за ними, но все равно пытался развить эту теорию. Тем не менее, он оказался полезным инструментом для многих областей. Альберт Эйнштейн согласился бы с этим. В качестве примера можно привести расчет электрических цепей переменного тока, что значительно облегчает применение функции по сложной цене. Теоремы любого рода, касающиеся распределения первого числа — пресловутой функции ром джита и связанных с ней теорем, по сути, гипотеза, поскольку она еще не доказана — являются одной из семи проблем тысячелетия. Было обнаружено, что сверхъестественные числа, которые являются So -Calculated Quaternions, применяются на месте. Здесь робототехника меня понимает. Кватернионы очень полезны при идентификации или определении положения трехмерных объектов в пространстве. И переезд в это дополнительное помещение дается нам труднее.
Несколько культур Китая, Индии, Египта, Центральной Америки и Месопотамии внесли свой вклад в развитие математики. А шумеры, жившие на территории современного Южного Ирака, первыми разработали систему измерения, основанную на 60.
Период зарождения математики
Считается, что основной период накопления математических знаний относится к периоду до н.э.
Первым доказательством математического предложения, вероятно, был древнегреческий мыслитель Талис Милисиос, живший в VII веке до н.э. с 625 по 545 год до н.э. Этот философ побывал во всех восточных странах. Согласно легенде, он учился у зулетов Египта и халдеев Вавилона.
Талис из Милета был привезен из Египта в Грецию. Первые понятия базовой геометрии: что такое диаметр, определение треугольника и т.д. Он предсказывал затмения и проектировал механические конструкции.
В это время постепенно формировалась арифметика, развивались астрономия и геометрия. Рождение алгебры и тригонометрии.
Период элементарной математики
Этот период начинается в 6 веке до н.э. Сегодня математика возникает как наука с теорией и доказательствами. Появляется теория чисел, учение о величине и ее измерениях.

Самым известным математиком этого периода является Евклид. Он жил в III веке до н.э. Он является автором первой сохранившейся теоретической реальности для математики.
Работа Евклида заложила основу так называемой эвклидовой геометрии, аксиомы которой основаны на фундаментальных понятиях, таких как точки, прямые, уровни и отношения.
В период элементарной математики зарождается теория чисел, а также учение об их величине и измерении. Впервые появляются отрицательные и неразделимые числа.
В конце этого периода возникает алгебра как буквенное исчисление. Сама наука алгебра представляется арабам как наука о решении уравнений. Арабское слово «алгебра» означает «восстановление», то есть перенос отрицательного значения в другую часть уравнения.
Период математики переменных величин
Основателем этого периода считается Рене Декарт, живший до 17 века. В своих трудах Декарт впервые ввел понятие переменных.
Это привело ученых к изучению констант и математическому описанию переменных и движений.
Этот период наиболее ярко охарактеризовал Фридрих Энгельс в своих трудах, в которых он писал.
Поворотным пунктом в математике стала декартова переменная. Благодаря этому движению и директ, он вошел в математику и сразу же стал необходимым для этого исчисления. Это произошло быстро и было не изобретено Ньютоном и Лейбницем, а усовершенствовано в целом».
Понятие «число» первоначально относилось к натуральным числам. Затем оно постепенно расширялось, включая целые числа, рациональные числа, действительные числа, комплексные числа и другие числа.
Понятие числа. Виды чисел
Это одно из основных определений математики. Все виды чисел возникают в результате необходимости выполнения людьми определенных вычислений. Потребность в информации о количестве объектов привела к концепции натуральных чисел и бесконечных натуральных чисел. Необходимость измерения площади, длины и объема привела к появлению рациональных чисел. Комплексные числа были введены для решения сложных уравнений.
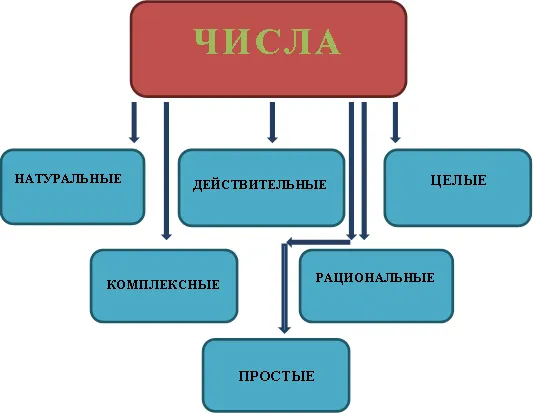
- Натуральные числа — это числа, получаемые при определении количества 1,2,3. Множество таких чисел принято обозначать буквой N. Например: 1,2,3 …..
- Целые числа. Определение понятия формулируется так: множество натуральных, отрицательных чисел и нуль. Их принято обозначать буквой Z. Например: -2,-1,0,1,2,3,4…..
- Рациональные числа. В понятие рационального числа входят дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Обозначаются буквой Q. Например: 2/3, -4/5
- Действительные. В понятие действительного числа включены рациональные и иррациональные числа, которые могут записываться в виде обычной и десятичной конечной и бесконечной дробей, а также нуль. Обозначаются буквой R. Например: 1245, 5⅔, -648,35
- Простыми называют натуральные числа, которые можно представить в виде двух множителей — единицы и самого этого числа. Обозначается буквой Р. Например: 1,3,7,11….
- Также существуют Иррациональные числа – это числа, не являющиеся рациональными, то есть нельзя представить в виде дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Например, число пи=3,1415926535, число e=2.718281828, квадратный корень из 3 и так далее.
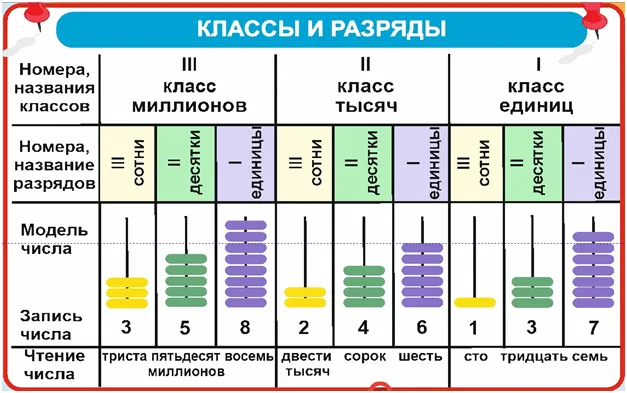
Классы и разряды чисел
Когда число представлено в виде одной цифры (5,9), оно называется однозначным, в виде 2 (24,31), 3 (211,984) цифр, 2 цифр, 3 цифр и даже (1893,100561) ) просто многозначным.
Все существующие цифры сгруппированы в классы и разряды натуральных чисел. Расположение цифр в числе называется классом числа. Самая маленькая цифра — это цифра единицы, за ней следуют десятки, сотни и тысячи.
Количество цифр в классе равно 3. Максимальное количество классов единиц равно 9, а максимальное количество классов тысяч равно 999999.
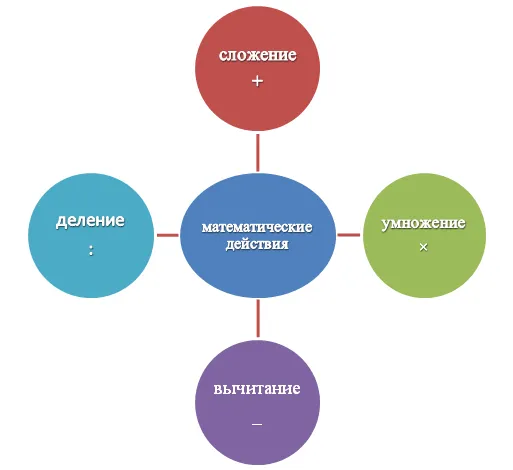
Математические действия
Математика не может существовать без арифметики. Всего существует четыре типа арифметических операций.
Порядок выполнения математических действий в выражениях со скобками и без скобок
Существует также последовательность математических операций, которые можно запомнить и легко решить любую сложную задачу. Порядок зависит от наличия или отсутствия скобок и рекомендуемого действия.
Без скобок действия выполняются в обычном порядке. Ниже приведен правильный порядок математических операций для примера без скобок.
В любом выражении умножение или деление должно выполняться первым по порядку. Ниже приведен правильный порядок арифметических действий без скобок.
Если выражение содержит круглые скобки, то сначала подсчитывается действие в круглых скобках, а затем по очереди все остальные действия. Последовательность математических операций, необходимых в скобках, следующая.
Это очень просто. Если вы не можете запомнить сразу, можете использовать этот урок как порошок!
Следующий интересный момент заключается в том, что каждый компонент математической энергии имеет свое название.
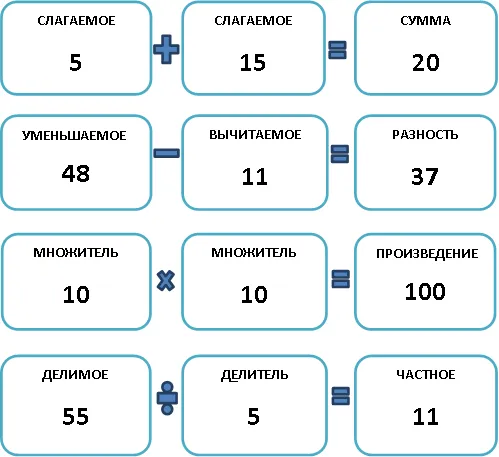
Правила нахождения неизвестного компонента при выполнении математических действий
Чтобы максимально упростить решение задач и уравнений, существуют специальные правила для нахождения неизвестных элементов.
-Чтобы найти одну из сумм, нужно из общего числа вычесть вторую сумму.
-Чтобы найти десятичную точку, достаточно найти сумму разности и десятичной точки.
-Чтобы найти вычитаемое, вычтите разность из вычитаемого.
-Чтобы найти коэффициент, найдите коэффициент произведения и второго коэффициента
-Чтобы найти неизвестный делитель, найдите произведение делителя и делимого.
-Чтобы найти неизвестный делитель, разделите делимое на делитель
Основные законы выполнения действий (перместительный, сочетательный, распределительный)
Чтобы правильно и быстро выполнять арифметические действия, необходимо всегда помнить основные законы, которые упрощают даже самые сложные процессы вычислений.
Законы сложения и умножения.
Сформулируйте законы сложения. Если переставить местами слагаемые, то суммы останутся прежними.
Напишите равенство для дополнительных транснациональных законов a+b+a
21+39 = 60 или 39+21 = 6015 x 3 = 45 или 3 x 15 = 45
Использование законов умножения.
Сформулируйте закон умножения. При перестановке множителей произведение остается неизменным.
Напишите уравнение для закона умножения a*b = b*a.
Кроме того, ввести в действие закон о комбатантах.
Сформулируйте дополнительные комбинационные законы. Чтобы сложить числовое значение и числовую сумму, достаточно найти сумму числового значения и любого слагаемого и прибавить вторую сумму
Напишите уравнение, представляющее дополнительный комбинированный закон a+(b+c) = (a+b)+c = a+b+c
Пример дополнительного метода комбинирования:.
20+(60+10) = 90 или 20+(60+10) = 90 или 20+(60+10) = 20+60+10 = 90
Математика — это наука, исторически основанная на решении задач о количественных и пространственных отношениях в реальном мире путем идеализации присущих объектам свойств и стандартизации этих задач. Эта наука занимается изучением числа, структуры, пространства и трансформации.
Развитие исчисления
Исаак Ньютон и Готфрид Либнц заложили основы бухгалтерского учета в 17 веке. Развитие исчисления пережило три периода: ожидания, роста и строгости.
На этапе ожидания математики пытались использовать методы, включающие бесконечные шаги, чтобы найти площадь под кривой или максимизировать определенные свойства. На этапе разработки Ньютон и Лейбниц объединили эти методы с помощью производных (кривые математических функций) и интегралов (области под кривой). Хотя их методы не всегда были достаточно корректными, математики 18 века достигли строгой стадии и смогли обосновать свои методы и создать конечную стадию исчисления. Сегодня мы определяем дифференциацию и интеграцию в терминах границ.
В отличие от бухгалтерского учета (работа с вещественными числами), который является разновидностью непрерывной математики, другие математики используют более теоретический подход. Дискретная математика — это отрасль математики, которая имеет дело с объектами, которые могут принимать только отдельные, изолированные значения.
Почему математика важна
Люди часто задаются вопросом, какое значение имеет математика в повседневной жизни. В современном мире математика, в том числе прикладная, не просто важна, она имеет решающее значение. Прикладная математика включает в себя области, изучающие естественный, биологический или социологический мир.
Области прикладной математики сегодня включают математическую физику, биологию, теорию управления, аэрокосмическую инженерию и финансы. Общим подходом к прикладной математике является создание математических моделей явлений, их решение и разработка рекомендаций по улучшению работы.
Хотя это не обязательно противоположность прикладной математике, чистая математика занимается абстрактными проблемами, а не проблемами реального мира. Большинство проблем, которыми занимаются чистые математики, имеют корни в конкретных физических проблемах. Такие абстрактные проблемы и технические сложности пытается решить чистая математика, которая привела к важным для человечества открытиям, включая глобальную машину Тьюринга.
Сложная математика, задействованная в чистой и прикладной математике, непостижима для большинства людей, но решения, разработанные в этом процессе, повлияли и улучшили жизнь многих людей.








