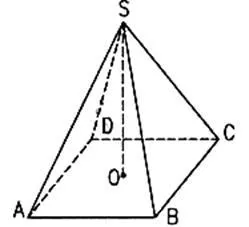
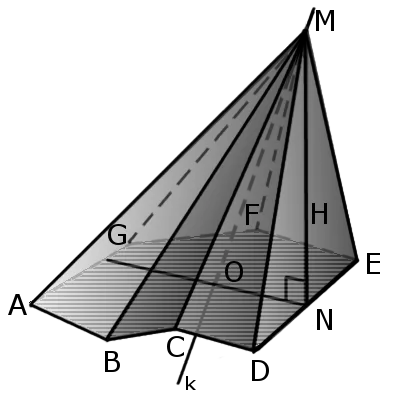
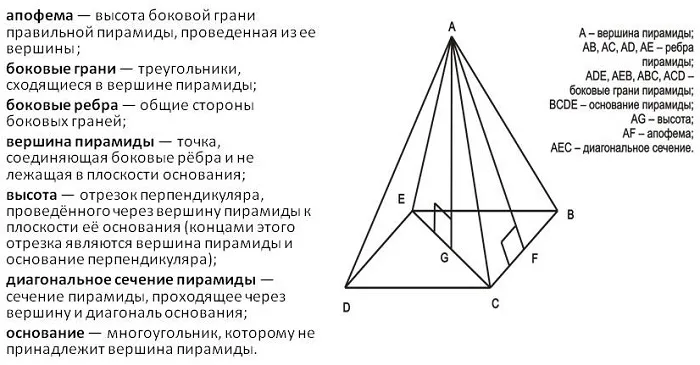
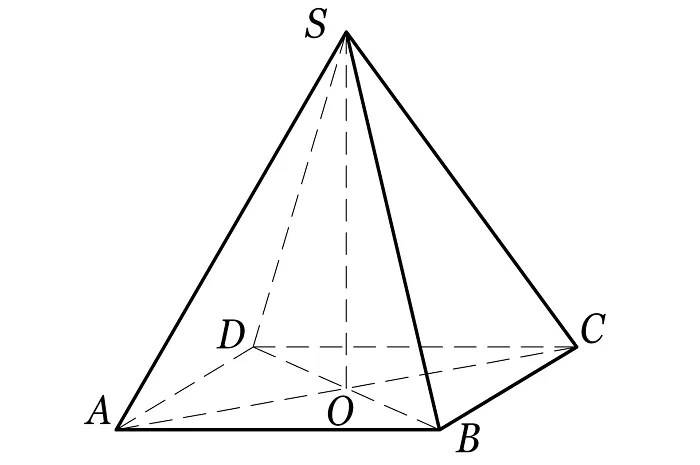
- Основание (четырехугольник ABCD) – грань фигуры, являющая многогранником. Ей не принадлежит вершина.
- Вершина пирамиды ( точка E) – общая точка всех боковых граней.
Элементы пирамиды.
- апофема — высота боковой грани правильной пирамиды, которая проведена из ее вершины (кроме того, апофемой является длина перпендикуляра, который опущен из середины правильного многоугольника на 1-ну из его сторон);
- боковые грани (ASB, BSC, CSD, DSA) — треугольники, которые сходятся в вершине;
- боковые ребра ( AS , BS , CS , DS ) — общие стороны боковых граней;
- вершина пирамиды (т. S) — точка, которая соединяет боковые ребра и которая не лежит в плоскости основания;
- высота ( SO ) — отрезок перпендикуляра, который проведен через вершину пирамиды к плоскости ее основания (концами такого отрезка будут вершина пирамиды и основание перпендикуляра);
- диагональное сечение пирамиды — сечение пирамиды, которое проходит через вершину и диагональ основания;
- основание (ABCD) — многоугольник, которому не принадлежит вершина пирамиды.
Свойства пирамиды.
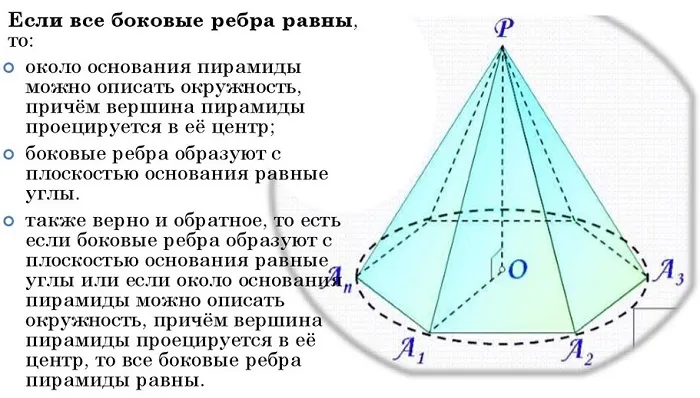
1. если все боковые грани имеют одинаковый размер, то: 2. если все боковые грани имеют одинаковый размер, то: 3. если все боковые грани имеют одинаковый размер, то: 4.
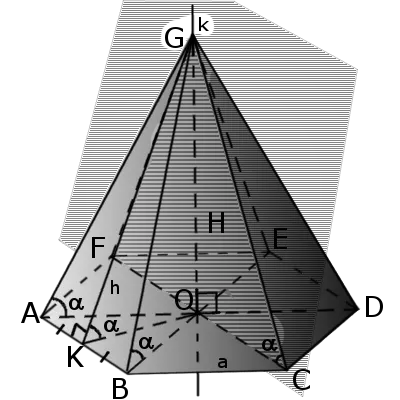
- около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
- боковые ребра образуют с плоскостью основания одинаковые углы;
- кроме того, верно и обратное, т.е. когда боковые ребра образуют с плоскостью основания равные углы, либо когда около основания пирамиды можно описать окружность и вершина пирамиды будет проецироваться в центр этой окружности, значит, все боковые ребра пирамиды имеют одинаковую величину.
2. если боковые грани имеют угол наклона к плоскости основания одинаковой величины, то: 3.
- около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
- высоты боковых граней имеют равную длину;
- площадь боковой поверхности равняется ½ произведения периметра основания на высоту боковой грани.
3. вокруг пирамиды можно нарисовать сферы, если в основании пирамиды есть многоугольник, который можно нарисовать в виде окружности (необходимое и достаточное условие). Центры сфер являются точками пересечения плоскостей, проходящих через центры граней пирамид, перпендикулярных к ним. Из этой теоремы следует, что сферы могут быть описаны как вокруг любого треугольника, так и вокруг любой обычной пирамиды.
4. сфера может быть вписана в пирамиду, если уровни биссектрис внутренних биссектрис пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка является центром сферы.
5. конус вписан в пирамиду, если вершины совпадают и основание конуса вписано в основание пирамиды. Поэтому конус может быть вписан в пирамиду только в том случае, если его котировки имеют равные значения (необходимое и достаточное условие).
6. конус описан вокруг пирамиды, если вершины совпадают, а основание конуса описано вокруг основания пирамиды. Конус может быть описан вокруг пирамиды только в том случае, если все боковые грани пирамиды имеют одинаковое значение (необходимое и достаточное условие). Эти конусы и пирамиды имеют одинаковую высоту.
7.Цилиндр вписан в пирамиду, если его первое основание совпадает с окружностью, вписанной в пересечение пирамиды с плоскостью, параллельной основанию, а второе основание принадлежит основанию пирамиды.
8. цилиндр описан вокруг пирамиды, если вершина пирамиды принадлежит одному из ее оснований, а второе основание цилиндра описано вокруг основания пирамиды. Поэтому цилиндр можно описать вокруг пирамиды, только если основание пирамиды является вписанным многоугольником (необходимое и достаточное условие).
1. диагональное сечение — вторичная плоскость проходит через диагонали вершины и основания фигуры. Четырехугольная пирамида имеет две такие секции (по одной на диагональ).
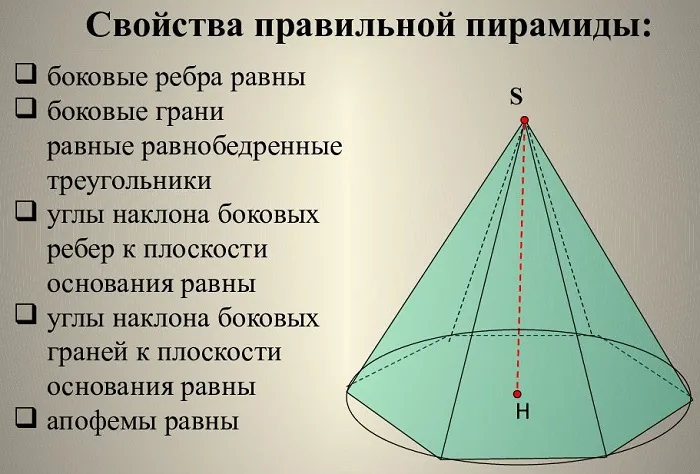
Правильные пирамиды. Свойства правильной пирамиды
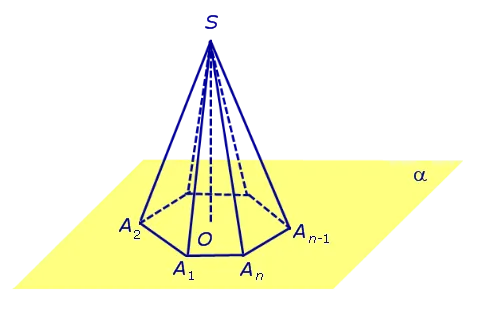
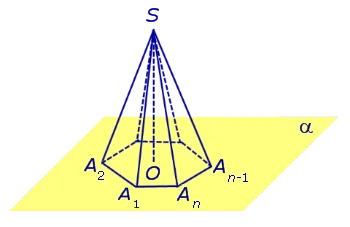
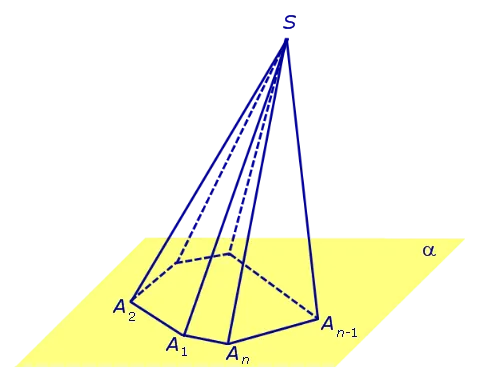
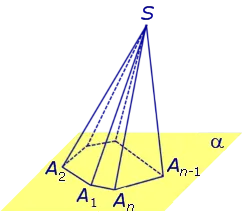
Примечание 2.Для центра основания A1 A2. An нормальной пирамиды SA.1 A2. An O, длина отрезка SO, обозначаемого O, равна высоте пирамиды. Часто само сечение SO называют высотой пирамиды, падающей с верхней S.
Определение 4. Высота граней нормальной пирамиды, падающих из вершины S, называется максимумом.
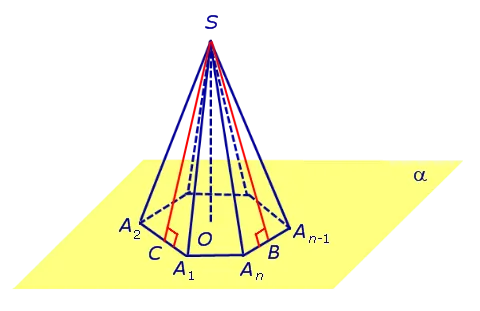
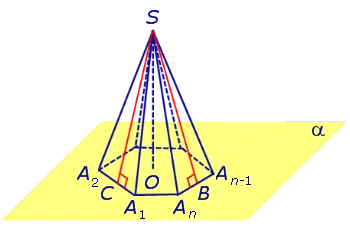
На рисунке 3 сечение SB является проекцией грани SA.nA n -1 Сегмент SC является проекцией лица SA.2 A1 n -1.
Замечание 3. Нормальная пирамида с n углами может иметь n запасов.
Свойства нормальных пирамид:.
Все ребра нормальной пирамиды равны .
Грани всех сторон нормальной пирамиды — равные равнобедренные треугольники.
В каждой нормальной пирамиде все запасы равны .
Ребра всех граней нормальной пирамиды образуют угол, равный плоскости основания пирамиды.
Ребра всех граней нормальной пирамиды образуют двугранный угол, равный плоскости основания пирамиды.
Тетраэдры. Правильные тетраэдры
Определение 5. Любая треугольная пирамида называется тетраэдром.
Претензия. В обычной треугольной пирамиде противоположные грани попарно перпендикулярны.
Доказательства. Рассмотрим пару обычных треугольников SABC и их противоположные грани. AC и BS. Среднее значение AC обозначается D. Поскольку отрезки BD и SD являются медианами равнобедренных треугольников ABC и ASC, BD и SD перпендикулярны AC (рис. 4).
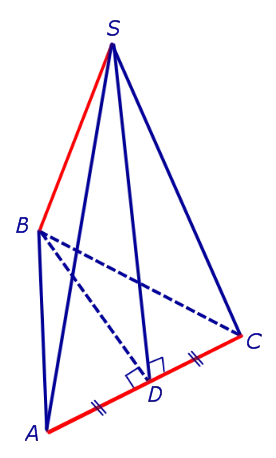
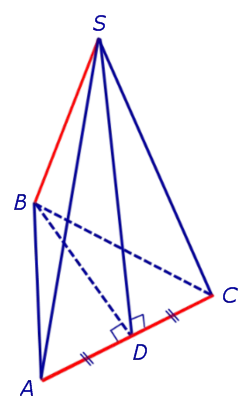
Исходя из перпендикулярности прямых и плоскостей, делаем вывод, что AC перпендикулярна плоскости BSD. Следовательно, AC перпендикулярна BS, что и требовалось доказать.
Определение 6. Тетраэдр, все грани которого равны, называется тетраэдром (рис. 5).
Проблема. Найдите высоту тетраэдра с ребром a.
Решение. Рассмотрим обычный тетраэдр SABC. Пусть O — подножие перпендикуляра, проведенного из вершины S к плоскости ABC. Поскольку SABC является правильным тетраэдром, O является точкой пересечения перпендикулярных линий равнобедренного треугольника ABC. Таким образом, мы имеем
где D — среднее значение AC (рис. 6).
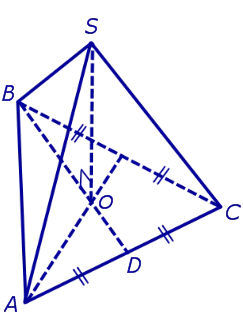
Используя теорему Пифагора, из треугольника BSO
Формулы для объема, площади боковой и полной поверхности пирамиды
Давайте представим следующую символику
| V | объем пирамиды |
| Sсторона | площадь боковой поверхности пирамиды |
| SЗавершение | площадь полной поверхности пирамиды |
| SГлавная | площадь основания пирамиды |
| PГлавная | периметр основания пирамиды |
Затем для расчета объема, сторон и общей площади пирамиды применяются следующие уравнения: .
На рисунке 3 сечение SB является проекцией грани SA.nA n -1 Сегмент SC является проекцией лица SA.2 A1 n -1.
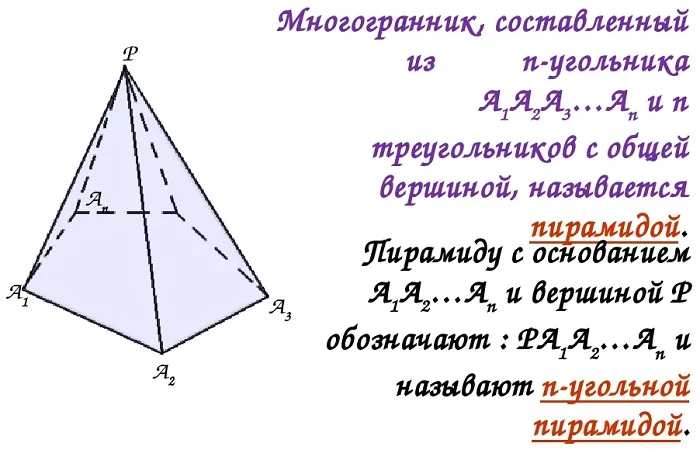
Что такое пирамида: определение, элементы, виды, варианты сечения
В этом материале объясняется определение, основы, типы и возможные вариации секций пирамиды. Представленная информация сопровождается пояснительным планом для лучшего понимания.
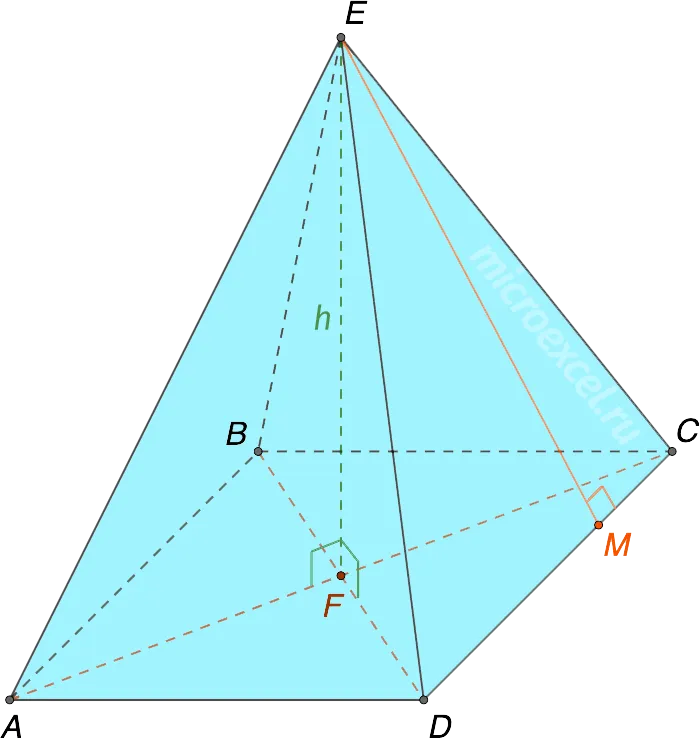
Пирамида — это геометрическая фигура в пространстве. Это многогранник, состоящий из основания и граней (с общими вершинами), количество которых зависит от количества углов в основании.
Примечание: Пирамиды являются частным случаем конусов.
Элементы пирамиды
- Основание (четырехугольник ABCD) – грань фигуры, являющая многогранником. Ей не принадлежит вершина.
- Вершина пирамиды ( точка E) – общая точка всех боковых граней.
Пирамида — это фигура, получаемая в результате «разрезания» пирамиды, то есть объединения всех граней на одном уровне пирамиды. В случае обычной четырехугольной пирамиды колесо на уровне основания имеет следующую форму
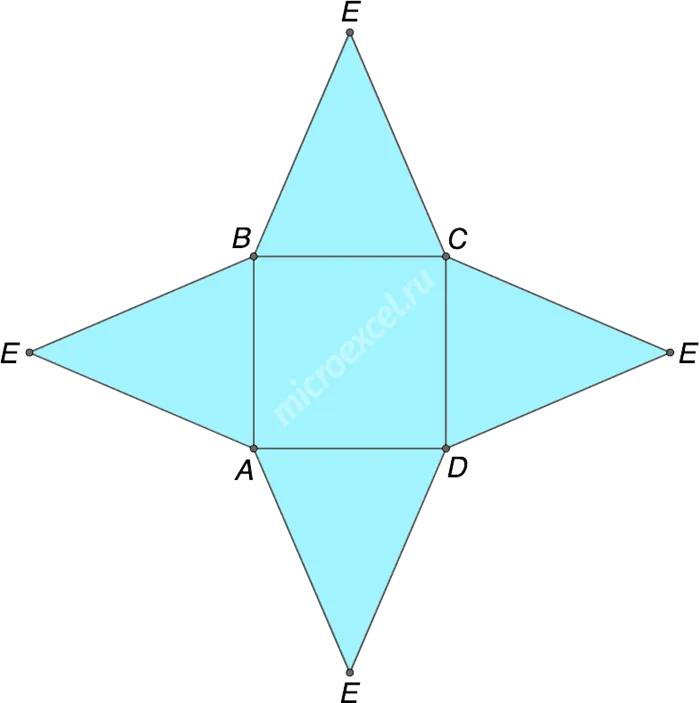
Примечание: Свойства пирамиды показаны в отдельном посте.
Виды сечения пирамиды
1. диагональное сечение — вторичная плоскость проходит через диагонали вершины и основания фигуры. Четырехугольная пирамида имеет две такие секции (по одной на диагональ).
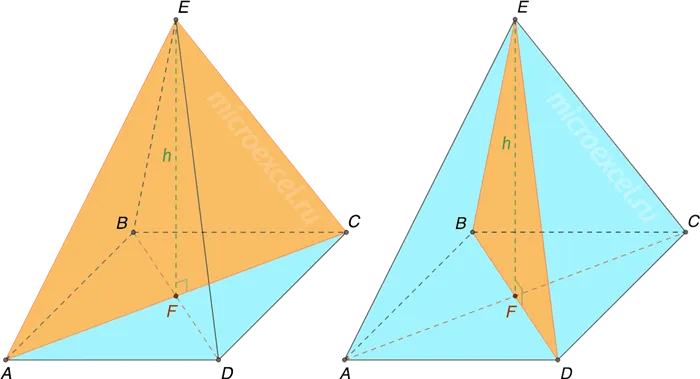
2 — Если вторичные плоскости параллельны основанию пирамиды, то пирамида делится на две фигуры. Идентичная пирамида (считая от вершины) и усеченная пирамида (считая от основания). Поперечное сечение представляет собой многоугольник, аналогичный основанию.
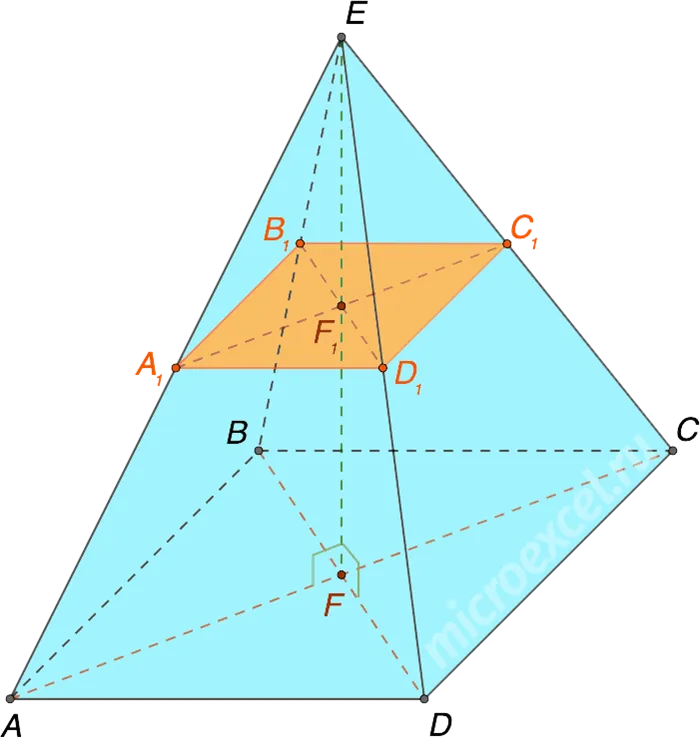
Примечание: Существуют и другие типы сечений, но они менее распространены.
Задача №2: Основанием пирамиды DABC является треугольник ABC с AB = AC = 13 см и BC = 10 см. Грань AD перпендикулярна плоскости основания и равна 9 см. Найдите площадь стороны пирамиды.
Свойства правильной пирамиды
7. вокруг пирамиды можно описать сферу. Центр очерченной сферы является точкой пересечения перпендикулярных линий, проходящих через центр края.
8.Сфера может быть вписана в пирамиду. Центр вписанной сферы является точкой пересечения биссектрис, исходящих из угла между ребром и его основанием.
9.Если центр вписанной сферы совпадает с центром вписанной сферы, то сумма плоских углов при вершине равна π, и наоборот, угол равен π/ n. где n — число. угла в основании пирамиды.
Связь пирамиды со сферой
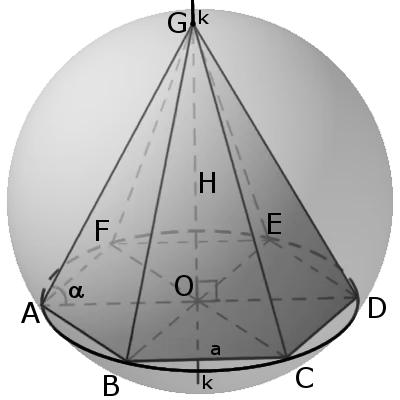
Если в основании пирамиды есть многогранник, на котором можно провести окружность, то вокруг пирамиды можно провести сферу (необходимое и достаточное условие). Центр сферы является точкой пересечения плоскостей, проходящих перпендикулярно центру боковых граней пирамиды.
Всегда можно описать сферу вокруг треугольной или нормальной пирамиды.
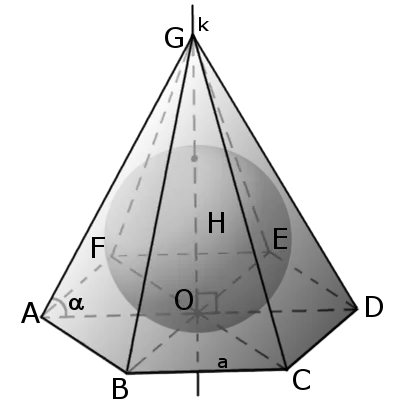
Сфера может быть зарегистрирована в пирамиде, если уровни разделов внутренних углов пирамиды пересекаются в одной точке (необходимое и правомочное условие). Эта точка является центром сферы.
Связь пирамиды с цилиндром
Если вершина пирамиды находится в основании цилиндра, а основание пирамиды записано на другом основании цилиндра, то пирамида записывается на ролике.
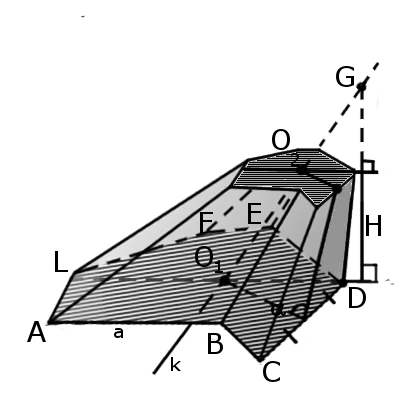
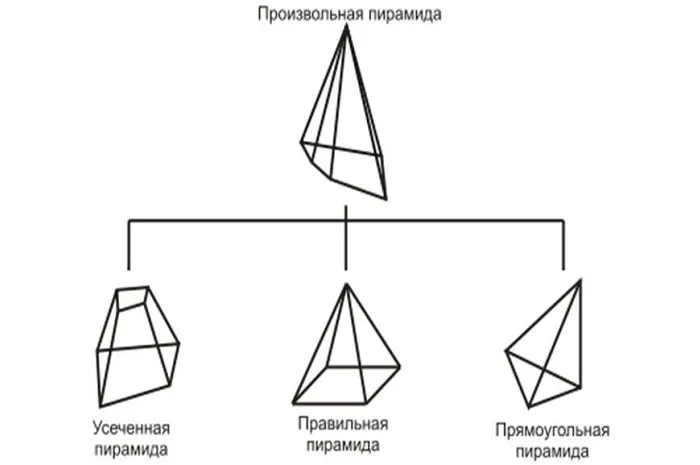
Значение. Пирамида с разрезом (призма пирамиды) — это многогранник, расположенный между основаниями пирамиды и уровнем разреза, параллельного основанию. Таким образом, пирамида имеет большее основание и меньшее основание, которое похоже на самое большое основание. Боковые стороны трапециевидные.
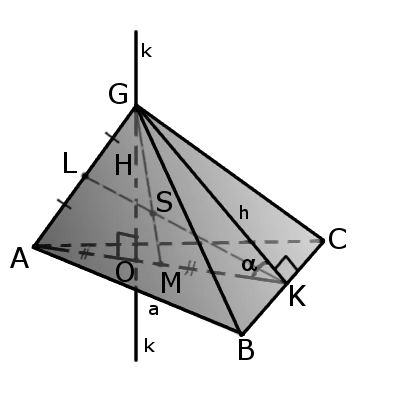
Значение. Треугольная пирамида (тетраэдр) — это пирамида, три грани и основание которой произвольно треугольные.
Тетраэдр имеет четыре грани, четыре вершины и шесть ребер; два ребра не имеют общих вершин, но не касаются друг друга.
Участок, соединяющий вершину тетраэдра с центром противоположной грани, называется медианой четырехслойного слоя (GM).
Двусторонним является отрезок, соединяющий средние значения не смежных противоположных граней (kl).
Все двухсторонние страны в четырехстороннем слое и друг друга пересекаются в одной точке. Двусторонняя разделена по центру, а срединная — в соотношении 3:1, начиная сверху.
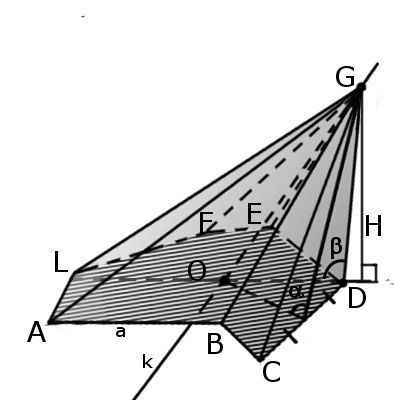
Значение. Наклонная пирамида — это пирамида, у которой одна из граней образует с основанием тупой угол (b).
Значение. Прямоугольная пирамида — это пирамида, у которой одно из боковых ребер перпендикулярно основанию.
Значение. Пирамида с острым углом — это пирамида, бурса которой длиннее половины длины основания.
Значение. Пирамида с тупым углом — это пирамида, в которой абсцисса составляет менее половины длины основания.
Значение. Нормальный тетраэдр — это тетраэдр, все четыре грани которого являются равными треугольниками. Это один из пяти нормальных многоугольников. В обычном тетраэдре два угла граней (между фасадами) и три угла (при вершине) равны.
Значение. Прямоугольный тетраэдр — это тетраэдр с прямым углом между тремя верхними гранями (грани вертикальны). Три ребра образуют прямоугольный тетраэдр, грани — прямоугольные треугольники, а основание — любой треугольник. Апофеоз появления равен половине сторон основания, с которого падает апофеоз.
Значение. Правильный тетраэдр — это тетраэдр, грани которого равны друг другу, а основание — прямоугольный треугольник. Грани такого тетраэдра — равнобедренные треугольники.
Значение. Ортоцентрированный тетраэдр — это тетраэдр, в котором в какой-то момент все высоты (перпендикуляры) падают с вершины на противоположную грань.
Значение. Дипирамида — это многогранник, состоящий из двух различных пирамид с общим основанием (пирамиды также могут быть гранеными), вершины которых находятся по разные стороны от уровня основания.
Основание — обычный треугольник, а вершины ߡ (ߡ displaystyle s \) проецируются на пересечение высот этого треугольника (через который они также прогрызаются).
Объем пирамиды
Главная формула объема пирамиды
Откуда взялся \ \ displaystyle s \ frac \)?
Не все так просто, сначала нужно вспомнить, что пирамиды и конусы имеют ෂ (displaystyle \ frac) в виде объема, а цилиндры — нет.
Давайте теперь рассчитаем объем самой популярной пирамиды.
Объем правильной треугольной пирамиды
Предположим, что сторона основания равна ዄ (⌘ displaystyle a \), а конец стороны — ዄ (⌘ displaystyle b \). \Найдите \ (⌘ displaystyle _> \) и ퟃ (ퟃ displaystyle H \).
\(⌘ displaystyle _> \) — площадь правильного треугольника ⌘(⌘ displaystyle ABC \).
Вспомните, как найти эту область.
Используйте тип области:.
\ (⌘ displaystyle S = \ fracab \ cdot \ sin \ gamma \)
Существует හ (හ displaystyle a \) — это также හ (හ displaystyle a \) и හ (හ displaystyle b \) — это также හ (හ displaystyle a \) и හ (හ displaystyle \ sin sin \ gamma = 쒰sin 60).<>^ \ displaystyle circ = \ frac> \)
Здесь мы находим ߋ(ߋ displaystyle H \).
Теорема Пифагора для \(\ displaystyle \ Delta SOC \)
Что такое \(\ displaystyle OC \)?
Это радиус окружности \(⌘ displaystyle \ Delta ABC \). Это потому, что пирамида правильная, и поэтому \(\ displaystyle OC \) является центром \(\ displaystyle \ Delta ABC \).
Найдите \(\ displaystyle OC \) (подробнее см. раздел «Прямоугольный треугольник»).
\(⌘ displaystyle OC = \ fracCK \), потому что \(⌘ displaystyle O \) также является пересечением сред.
\(⌘ displaystyle C ^> = A ^>-A ^> \) (⌘ displaystyle \ Delta ACK \) Теорема Пифагора.
\Заменим 슰 (슰 displaystyle OC \) в выражении для 슰 (슰 displaystyle H \).
И давайте заменим их все типами опухолей:…
Внимание: если существует тетраэдр. \ (⌘ displaystyle b = a \)), формула становится.
Объем правильной четырехугольной пирамиды
Предположим, что стороны основания равны ⌘ (⌘ displaystyle a \), а края сторон равны ⌘ (⌘ displaystyle b \).
Здесь не нужно искать \(\ displaystyle _> \). В конце концов, нижняя грань — квадрат, поэтому это \(\ displaystyle _> => \).
Давайте найдем \(\ displaystyle H \). Теорема Пифагора для \(\ displaystyle \ Delta SOD \)
Вы знаете \(\ displaystyle OD \)? Часто почти. Смотрите:.
Замените \(\ displaystyle OD \) выражением \(\ displaystyle H \).
Затем он заменяет оба типа объема \(\ displaystyle H \) и \(\ displaystyle _> \).
Объем правильной шестиугольной пирамиды

⥉ (⌘ displaystyle a \) и боковой край ⥉ (⌘ displaystyle b \) для бокового края основания ⥉ (⌘ displaystyle b \).
\Как найти \(⌘ displaystyle _> \)? Как видите, шестиугольник \(⌘ displaystyle ABCDEF \) состоит ровно из шести одинаковых прямоугольных треугольников. Мы уже искали площадь прямоугольного треугольника, когда вычисляли объем пирамиды из прямоугольных треугольников. Здесь мы используем найденную формулу.
Значение. Правильный тетраэдр — это тетраэдр, грани которого равны друг другу, а основание — прямоугольный треугольник. Грани такого тетраэдра — равнобедренные треугольники.
Формулы объема и площади поверхности пирамиды с примерами расчета
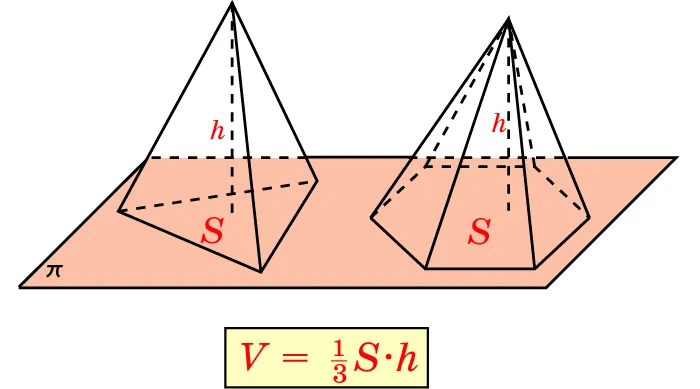
Объем можно рассчитать по следующей формуле
где используются следующие символы.
Общая площадь может быть рассчитана как сумма площадей основания и всех боковых треугольников.
Пример решения задачи
Если стороны основания равны 3 см, а боковые грани — 4 см, то высоту фигуры можно определить по теореме Пифагора.
Во-первых, согласно теореме Пифагора, она равна половине длины диагонали. Поскольку это квадратная диагональ, она равна квадратному корню из 18 (4,25 см).
Здесь мы рассмотрим четырехгранную пирамиду.
Используйте теорему Пифагора, чтобы найти высоту. Она составит приблизительно 4,5 см.
Площадь основания равна 3*3 = 9 квадратных сантиметров. Представьте его в виде квадрата с 3 см на каждой стороне. Подставляя значения из формулы объема, получаем
V = (1/3) * 9 * 4,5 = 13,5 см3
Чтобы вычислить площадь, нужно знать площадь основания квадрата и сторон треугольника. Для этого сначала воспользуйтесь теоремой Пифагора, чтобы найти длину запаса. Она равна 4,27 см.
Площадь обеих сторон равна 12,81 кв. см, а основания — 9 кв. см. Если сложить площади всех сторон, то получится 60,24 кв. см. Площадь поверхности можно рассчитать, изучив скан формы.








