Ромб — это прямоугольник с равными сторонами. Если известна одна сторона, площадь ромба вычисляется как произведение углов sin между сторонами на длину квадрата.
Площадь. Формулы площади
Площадь многоугольника связана с геометрической фигурой, такой как квадрат. Единичная площадь многоугольника равна площади квадрата со сторонами, равными 1. Давайте познакомимся с двумя основными свойствами понятия площади многоугольника.
Далее, основными геометрическими областями планетометрии являются. Квадраты, прямоугольники, прямоугольники, трапеции и треугольники показаны без выделения.
Площадь треугольника
Площадь треугольника определяется как половина произведения длин его сторон на высоты, проведенные к этим сторонам, т.е.
Готовые работы на аналогичную тему
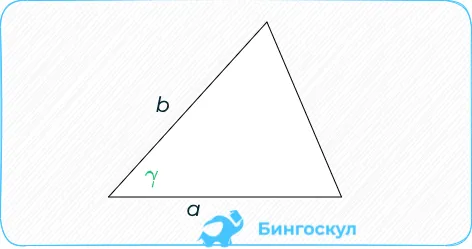
Площадь треугольника по теореме равна половине произведения длин смежных сторон на синус угла между этими сторонами.
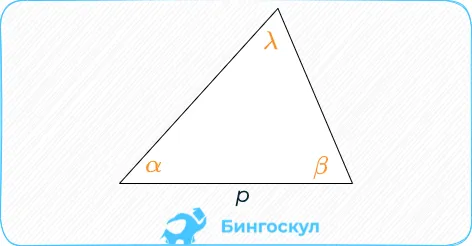
Предположим, что даны три стороны треугольника $a, ɑ b \ и ɑ c$. Тогда площадь этого треугольника выражается как
где $p$ — половина периметра треугольника.
Площадь прямоугольного треугольника со стороной $a$ определяется как
Предположим, что нам даны три стороны треугольника $a, Ј b \, Ј c $ и радиус $r$ вписанной в него окружности. Тогда площадь этого треугольника выражается как
где $p$ — половина периметра треугольника.
Предположим, что нам даны три стороны треугольника $a, ɑ b \, c $ и радиус $R$ описанной окружности. Тогда площадь треугольника выражается как
Пример задач
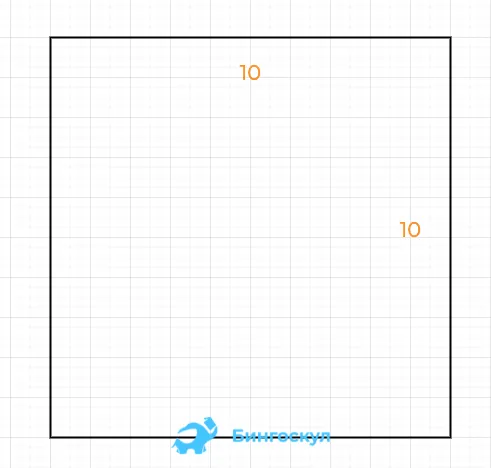
Если площадь клетки равна 1, найдите площадь фигуры, изображенной на рисунке $400.
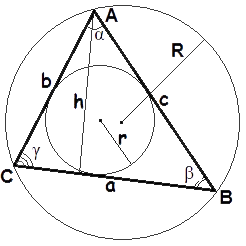
Это число можно классифицировать как

Если площадь клетки равна 1, найдите площадь фигуры, изображенной на рисунке 3500.
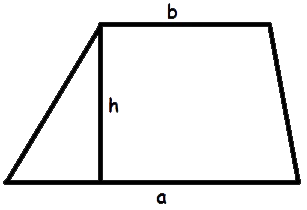
Это число можно классифицировать как

\ S _ = \ frac \ cdot 4 \ cdot 1 = 2, \ S _ = \ frac \ cdot 3 \ cdot 1 = 1,5, \ S _ = \ frac \ cdot 3 \ cdot 3 = 4,5, \ S _ = \ frac \ cdot 4 \ cdot 1 = 2
Если круг можно вписать в выпуклый четырехугольник, как в треугольник, то для нахождения площади четырехугольника необходимо определить два измерения: площадь круга и площадь треугольника.
Формула площади прямоугольника
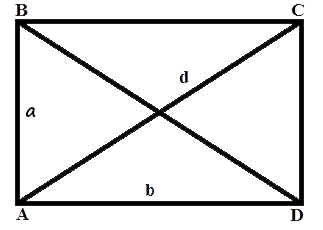
Формула для площади прямоугольника с длинами сторон и высотой Площадь прямоугольника равна произведению длины его стороны и длины высоты, приходящейся на эту сторону.
Укажите площадь прямоугольника из двух сторон и угла между ними Площадь прямоугольника равна произведению длин сторон на синус угла между ними.
Формула площади прямоугольника с двумя диагоналями и углом между ними Площадь прямоугольника равна половине произведения длин диагоналей на синус угла между ними.
Формулы площади ромба
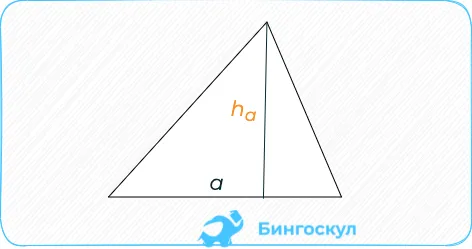
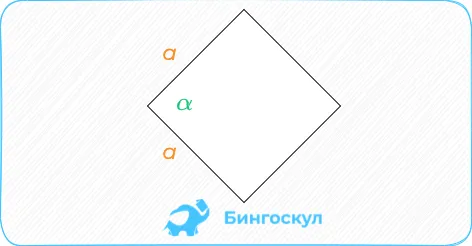
Укажите площадь ромба в терминах длины и высоты его сторон. Площадь ромба равна произведению длины его стороны и высоты, заданной для этой стороны.
Найдите площадь ромба с помощью длин сторон и угловПлощадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
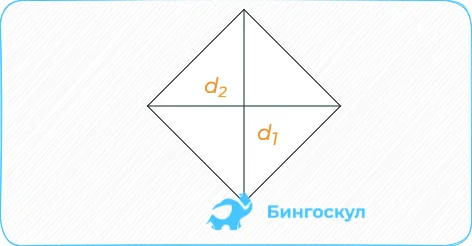
Введите площадь ромба и длину его диагоналей. Площадь ромба равна половине произведения длин его диагоналей.
Формулы площади выпуклого четырехугольника
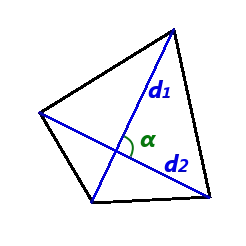
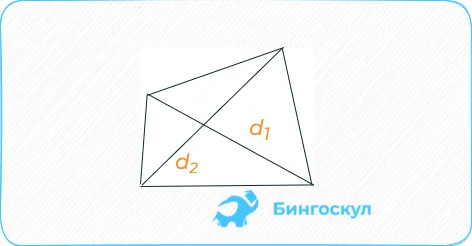
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на полутоновые углы:.
где S — площадь четырехугольника d1, d2 — длина диагоналей четырехугольника, а a — угол между диагоналями четырехугольника.
Площадь выпуклого четырехугольника равна произведению полуокружностей на радиусы внутреннего круга
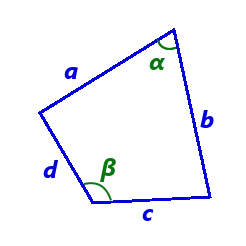
Формула для площади четырехугольника на основе длин сторон и угла между противоположными углами
a, b, c и d — длины сторон четырехугольника.
p = a + b + c + d 2 — полупериметр четырехугольника, the
θ = α +β2 — это половина суммы двух противоположных углов четырехугольника.
Человек в области квадрильи, который может описать цикл.
… Ровно помещается в ɑ (ɑ displaystyle a \ cdot b \) квадратных метров. Посмотрите внимательно: есть ዄ (ዄ displaystyle b \) «слоев», каждый из которых имеет ровно ዄ (ዄ displaystyle a \) квадратных метров.
Площади геометрических фигур: список формул, описание, примеры
Для практических целей иногда необходимо вычислить площадь геометрической фигуры. Например, необходимо измерить участки и поверхности во время ремонтных или строительных работ. Что такое площадь геометрической фигуры, используя типы, определенные в различных ситуациях.
Площадь — это числовая характеристика поверхности, указывающая на количество квадратов 1 x 1, которые занимает объект на плоскости. Существуют различные единицы измерения площади, такие как метры, сантиметры и километры.
Для прямоугольного четырехугольника это делается простым подсчетом и умножением цен. Пример квадрата — 100 см2 : 10 x 10 см.
В математике существует менее 12 фигур, площадь которых можно вычислить — это замкнутое множество, образованное точками. Общий принцип расчета формируется благодаря совершенному символизму.
Формулы площадей фигур по геометрии
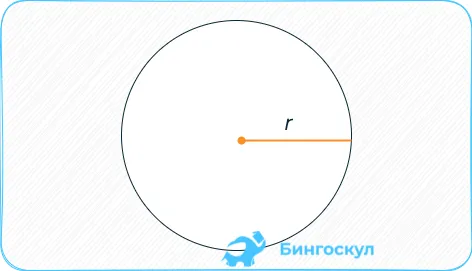
Если диаметр известен, то он равен квадратной четверти P.
Для s = \ pi \ frac, d = \ frac r, d^2 = \ frac r^2.
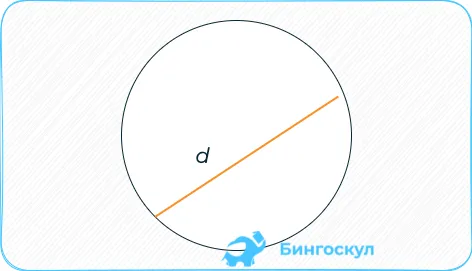
Кольцо окружности: разница между кольцом и циклом.
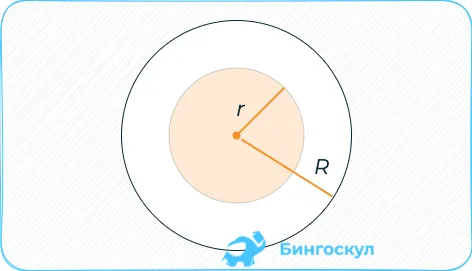
Четырёхугольники
Квадраты: размеры сторон увеличиваются.
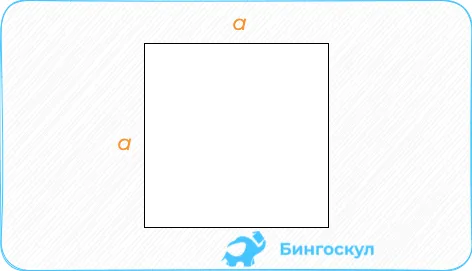
Площадь также рассчитывается как половина диагонали квадрата.
Прямоугольник: произведение смежных сторон — длина х ширина.
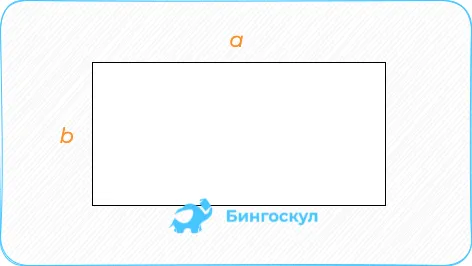
Прямоугольник: умножение длины одной стороны увеличивает высоту, на которую она приходится.
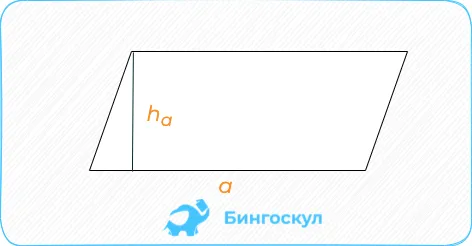
Второй тип применяется, когда длины сторон известны по углу между ними — произведению сторон на синус угла, который они пересекают.
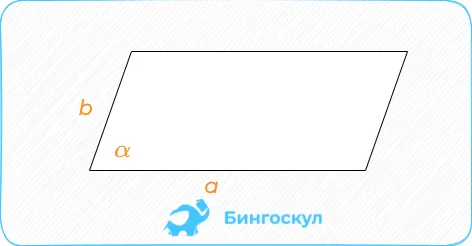
Ромб — это прямоугольник с равными сторонами. Если известна одна сторона, площадь ромба вычисляется как произведение углов sin между сторонами на длину квадрата.
Если дана длина диагонали, то площадь равна половине произведения диагоналей.
Если имеется одна диагональ (полудиагональ) и одна сторона, то неизвестные данные вычисляются по теореме Пифагора.
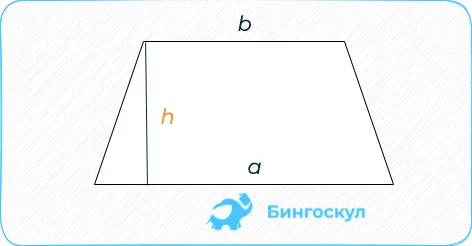
Трапеция: половина суммы верхнего и нижнего оснований высоты геометрической фигуры.
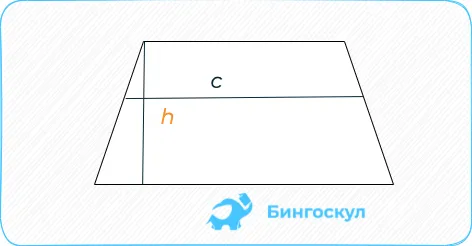
Учитывая среднюю линию и высоту, область умножается путем перемножения значений.
Если конфигурация четырехугольника такова, что не позволяет описать близлежащие окружности, то вид области будет несколько длиннее: s =√(p — a) (p — b) (p — c) (p — d) — ABCD COS 2 c.
С чего начинать
Самое время вспомнить школьную математику — для вычисления площади необходимы три параметра.
- Длина – обычно она бывает 4 либо 4,5 метра.
- Ширина – стандартное значение для большинства домов это 3 или 3,5 метра.
- Высота – в новостройках она обычно равна 2,5 метрам. А вот в постройках сталинской эпохи может составлять до 3 метров.
Для решения задачи вычисления площади нельзя обойтись без правильных инструментов.
- рулетки;
- строительного угольника;
- карандаша;
- калькулятора;
- строительного уровня.
Если вы планируете много писать, рекомендуется завести блокнот или тетрадь вместо бумаги. Листовки обычно теряются, и их не всегда легко найти, когда они нужны. Кассеты всегда должны иметь держатель. В противном случае могут возникнуть осложнения, и процесс расчета превратится в настоящую пытку.
Алгоритм проведения расчётов
Если все готово, можно приступать к расчету. Если вам нужно вычислить площадь поверхности нормальных фигур, то здесь нет ничего сложного — не забывайте об этих типах.
Если форма стен, пола и крыши сложная, то это совсем другое дело. В этом случае необходимо комбинировать различные методы. Это означает разделить помещение на различные квадраты и рассчитать площадь каждого из них. Затем удалите или добавьте их с общей поверхности.
Нет необходимости измерять длину стены вдоль юбки. Например, если мебель находится посередине, ее можно посчитать в соответствующих точках. Другими словами, достаточно, чтобы он был параллелен полу и потолку, выше, ниже и посередине. Никаких диагоналей, никаких тенденций! В противном случае расчет будет неверным.
Если возникнут трудности, вы всегда можете попросить помощи у кого-нибудь из домашних.
Правильная геометрия
При расчете площадей трудностей не возникает. Для простых прямоугольников достаточно измерить только стороны и высоту, так как противоположные стороны таких фигур равны. Для того чтобы комната имела правильные границы, достаточно применить строительные уголки по углам, но иметь чистую картину не всегда возможно.
Все знают тип прямоугольника для вычисления: прямоугольник.
Кажется, невозможно забыть тип для вычисления площади прямоугольника, но некоторые люди понимают его слишком много источников информации
Этот тип применяется для стен, потолков, полов, дверей, окон и других прямоугольных поверхностей. Для запланированного ремонта важно взять чистую стоимость. Для этого удалите участки стен, двери и окна с участков стен. Общая площадь всего помещения может быть рассчитана по следующему типу — H (a≤2+bb). где H — высота помещения.
Квадраты еще проще — пока вы измеряете одну сторону, измеряйте квадрат.
Помещения с неправильными очертаниями
Но как вычислить площадь помещения, если оно имеет неровные поверхности? Есть несколько великолепных оттенков:
- Стены. В мансардной комнате стена может иметь форму трапеции или треугольника.
- Потолок. В тех же мансардных помещениях данная плоскость может быть под определённым углом. Также есть варианты с ломаной поверхностью, когда несколько плоскостей пересекаются межу собой.
Но нет причин для беспокойства и нет необходимости разбираться с тригонометрией. Все, что вам нужно сделать, это визуально разделить сложную поверхность стены или крыши на различные простые уровни. Затем вычислите площадь каждой фигуры и сложите их вместе.
Чтобы ускорить процесс, мы приводим несколько типов областей, которые могут быть вам полезны:.
Прямоугольник:.
Треугольники:.
- S=0,5⋅b⋅h – по основанию и высоте.
- S=0,5⋅ab⋅sin(α) – по сторонам и углу.
- S=√(p·(p-a)·(p-b)·(p-c)) – формула Герона по трем сторонам.
Обозначения: пи — 3,14159, r — радиус, a, b, c — стороны, pi — периметр, h — высота, m — средняя линия.
Простое решение вопроса
Как рассчитать квадратные метры стены, крыши или пола, если в вашем распоряжении есть интернет, особенно если речь идет о сложных формах? В этом случае проект значительно упрощается. В Интернете есть множество электронных калькуляторов, которые выполняют все расчеты за считанные секунды. Все, что необходимо, — это установить соответствующие параметры.
Для удобства все измерения определяются в различных единицах в соответствии с особыми потребностями. Такие калькуляторы позволяют легко рассчитать не только площадь пола, но и площадь участка. Кроме того, результаты могут быть переведены в другие желаемые единицы измерения.
Этот тип применяется для стен, потолков, полов, дверей, окон и других прямоугольных поверхностей. Для запланированного ремонта важно взять чистую стоимость. Для этого удалите участки стен, двери и окна с участков стен. Общая площадь всего помещения может быть рассчитана по следующему типу — H (a≤2+bb). где H — высота помещения.
Площадь четырёхугольников
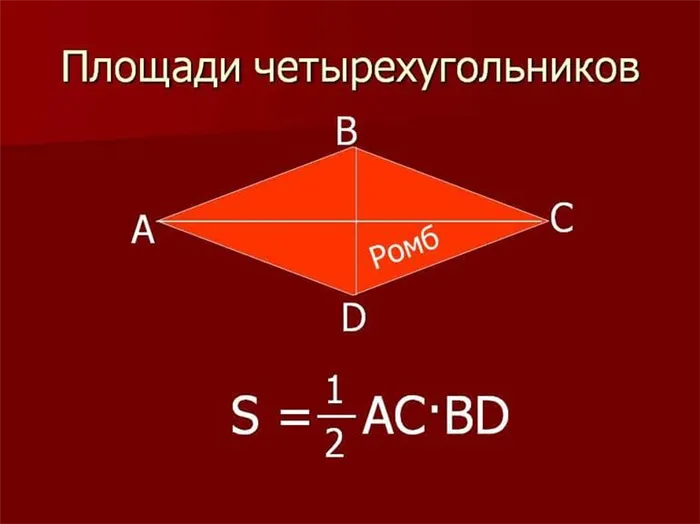
Четырехугольник — это одна из геометрических (многоугольных) фигур с четырьмя сторонами и четырьмя вершинами, три из которых не лежат на одной прямой. Четырехугольник называется выпуклым, если он лежит по одну сторону от линии, которая является продолжением любой стороны.
К криволинейным четырехугольникам относятся почти все известные фигуры с четырьмя вершинами и четырьмя сторонами. Их основные типы: 1) ромб — 2) прямоугольник — 3) стол — 4) квадрат — 5) прямоугольник.
Квадрат и прямоугольник
Самый простой способ вычислить площадь квадрата — это площадь самого квадрата, другими словами, длину его сторон (S = a 2). Это вычисление связано с особенностью квадрата — все стороны абсолютно равны друг другу, поэтому квадрат называют нормальной фигурой.
Существует второй, более сложный тип площади квадрата, где вычисления производятся через диагонали. Диагональ — это линия, соединяющая два угла, которые противоположны друг другу. Чтобы вычислить площадь, диагональ нужно возвести в квадрат, а следствие разделить на 2. S=½D2.
Для прямоугольника вид: s = a * b, где a и b — длины двух разных сторон, разделяющих вершину.
Параллелограмм, ромб и трапеция
Прямоугольник — это четырехугольник с двумя противоположными тупыми углами и двумя острыми углами.
Существует три типа прямоугольных областей.
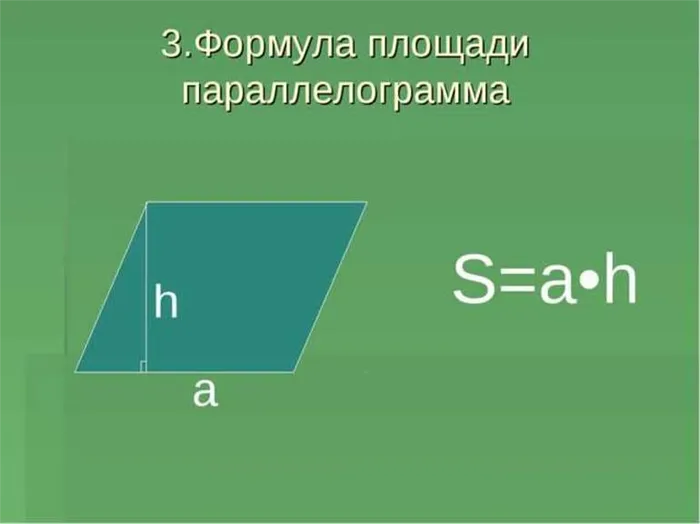
- Умножить сторону на высоту, перпендикулярную стороне: S = a * h.
- Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
- Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.
Ромб похож на прямоугольник с одним отличием: он равносторонний. Поэтому подобные типы используются для вычисления площади ромба.
Стол — это геометрическая фигура со следующими элементами: два параллельных основания, одно верхнее и одно нижнее, и две боковые стороны, образующие острый угол с нижним основанием. Для сторон длина может быть одинаковой (таблицы SO -Calcaled Isosceles) или разной.
Поскольку таблица состоит из прямоугольника и двух треугольников, можно использовать специальный тип: s=(a + b):| a + b | *√(p -a) *(p -b) *(p -a -c) *(p -α -d).
Этот тип имеет следующие символы
Выпуклый четырёхугольник

Круг и эллипс
Наиболее распространенным и широко используемым правилом для определения площади круга является умножение на число pi:s = pi * r 2 радиуса квадратного круга.
Число P, обозначаемое греческой буквой «P», является математической константой, полученной в результате деления на окружность с диаметром. P — это невыразимое число. Для расчета принимается среднее значение 3,14.
Вместо радиуса можно использовать диаметр окружности. Диаметр получается путем умножения квадрата на π и деления результата на 4. Тип: S = (π * D 2) / 4.
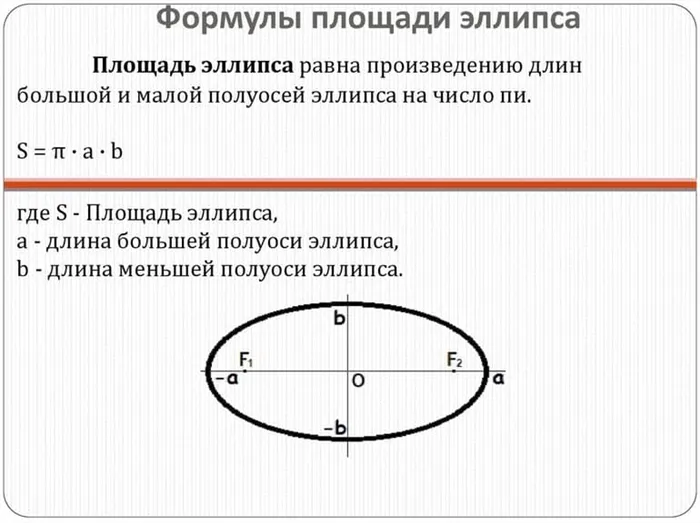
Для вычисления площади такой фигуры, как недостаток, необходимо построить две оси, т.е. две линии. То есть сами линии перпендикулярны друг другу (образуют прямой угол), так как каждая делит недостаток на две равные части. Точки пересечения образуют уннинги, выделяя каждую ось в середине.
Площадь дефекта рассчитывается как произведение трех размеров. Число P, длина большой полуоси (a) и длина малой полуоси (b): s = pi * a * b. Можно также использовать специальные электронные калькуляторы, позволяющие вычислять площади различных фигур.
s = a — h, где a — длина основания, а h — высота треугольника, проведенная к основанию.
Что такое площадь и как ее найти?
Площадь характерна для замкнутой геометрической формы (например, круг, квадрат, треугольник) и указывает на ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Он обозначается буквой s (квадрат).
1. самый известный вид площади треугольника, основанный на сторонах и высоте:.
s = a — h
где a — длина основания, а h — высота треугольника, проведенная к основанию.
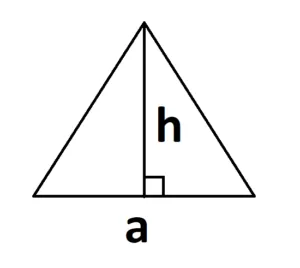
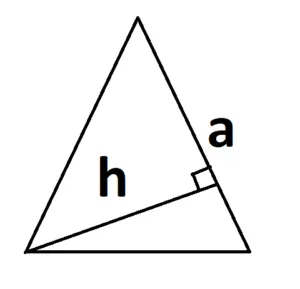
И основание не обязательно должно быть внизу. И это нормально.
Если треугольник тупой, то высота является продолжением основания.
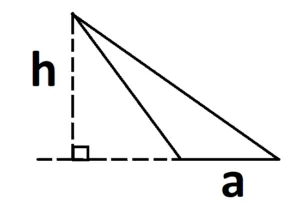
Если треугольник прямоугольный, то основание и высота являются его катетами.
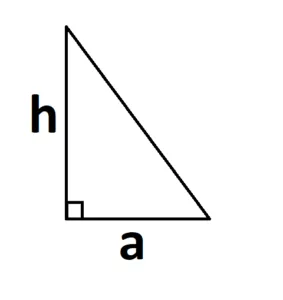
2.Другое уравнение, менее полезное, но почему-то всегда забываемое, следующее.
S=a—b—sinα
где a и b — две стороны треугольника, а sina — синус угла между этими сторонами.
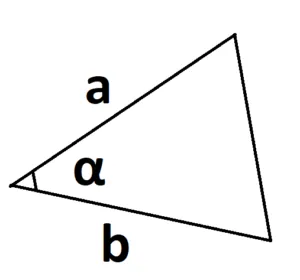
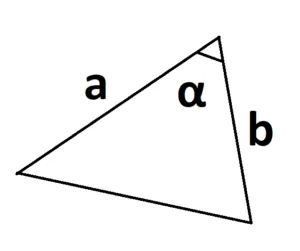
Основное предположение заключается в том, что угол берется между двумя известными сторонами.
3. тип площади трех сторон (тип цапли): s
S =
где a, b и c — стороны треугольника, а p — половина периметра. p = (a + b + c)/2.
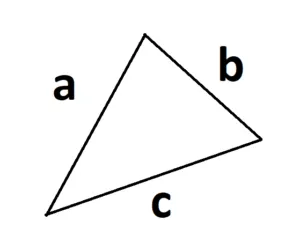
4. введите площадь треугольника через радиус окружности:.
S =
где a, b и c — стороны треугольника, а R — радиус окружности.
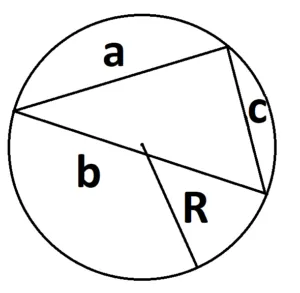
5. формула для площади треугольника через радиус окружности:.
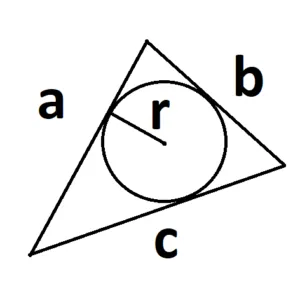
S = р-р
где p — полуокружность треугольника, а r — радиус эндоцикла.
(1) Поскольку квадрат — это прямоугольник, все стороны которого равны, то применяется следующая формула.
S = a-a = a 2
(2) Площадь квадрата можно также определить по его диагоналям: .
S = d 2
Как найти площадь круга?
1.Площадь круга можно найти по его радиусу: S
S = πr2
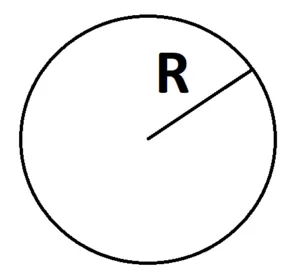
2. площадь круга можно найти по его диаметру: S=πd2/4
S=πd2/4








