Экстремумы функции. Как найти максимум функции

Другими словами, если x₀ — является точкой минимума функции f (x), а в интервале (a, b) функция f (x₀) меньше, чем все остальные значения функции.

Наибольшее и наименьшее значение функции

На практике производные необходимо использовать для вычисления максимального и минимального значений функции. Это делается при минимизации затрат, максимизации прибыли, расчете оптимальной загрузки производства и т.д., т.е. когда необходимо определить оптимальные значения параметров. Чтобы правильно решать такие задачи, необходимо хорошо понимать максимальное и минимальное значения функции.

Обычно эти значения задаются в интервале x. Это может соответствовать всему полю функции или его части. Это может быть либо интервал a? b, открытое пространство (a; b), (a; b, a; b), бесконечное пространство (a; b), (a; b, a; b) или бесконечное пространство -∞; a, (-∞; a, a; +∞), (-∞; +∞).

Этот документ описывает, как вычислить максимальное и минимальное значения явно заданной функции, используя переменную y = f(x) y = f(x).

Основные определения

Как обычно, мы начнем с базового определения.

Минимальное значение функции y = f (x) на интервале x — это значение m a x y = f (x 0)x ∈ X, при котором неравенство f (x) ≤ f (x 0) верно для любого значения x. ∈ X, x ≠ x 0.

Минимальным значением функции y=f(x) на некотором интервале x является значение minx∈Xy=f(x 0), что делает неравенство f верным для любого значения x∈X, x≠x 0. (X f (x) ≥ f (x 0)).

Эти определения вполне очевидны. Проще говоря, максимальное значение функции — это ее максимальное значение в известном интервале при x 0, а минимальное значение — это минимально допустимое значение в том же интервале при x 0.

Неподвижная точка — это значение аргумента функции, производная которой обращается в ноль.

Почему нам нужно знать, что такое неподвижная точка? Чтобы ответить на этот вопрос, нужно вспомнить теорему Ферма. Оказывается, неподвижная точка — это точка, в которой находятся экстремумы (т.е. минимумы или максимумы) дифференцируемой функции. В результате функция имеет минимальное или максимальное значение на заданном интервале в одной из точек остановки.

Функция также может принимать максимальное или минимальное значение в точке, где определена сама функция и не существует ее первая производная.

Первый вопрос, который возникает при изучении этой проблемы, — всегда ли можно определить максимальное или минимальное значение функции в заданном интервале. Нет, этого нельзя сделать, если границы пространства совпадают с границами поля или если вы имеете дело с бесконечным пространством. Функции также могут возникать на заданном интервале или на бесконечности и принимать минутные или бесконечные значения. В этих случаях невозможно определить наибольшее и/или наименьшее значение.

После разработки графика эти моменты становятся более понятными.

Наибольшее и наименьшее значение функции на отрезке

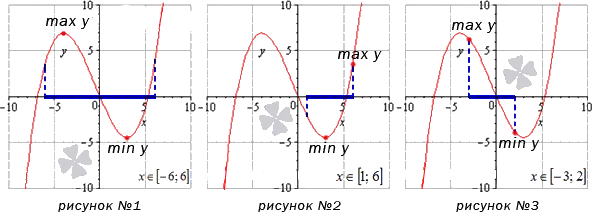
Первый график изображает функцию с максимальным и минимальным значениями (m axy и min y) в фиксированных десятичных точках в интервале -6. 6.6.

Рассмотрим подробнее случай, показанный на втором графике. Измените значение раздела на 1? 6 И мы видим, что максимальное значение функции достигается в точке, где дистальная ось находится в правом конце пространства, а минимальное — в фиксированной точке.

На третьей диаграмме отклонения точек представляют собой предельные точки участка -3. 2.2. они соответствуют максимальному и минимальному значениям конкретной функции.

Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до выкидыша). Если вы не можете написать работу самостоятельно, вы можете заказать ее здесь.

Экстремумы функции

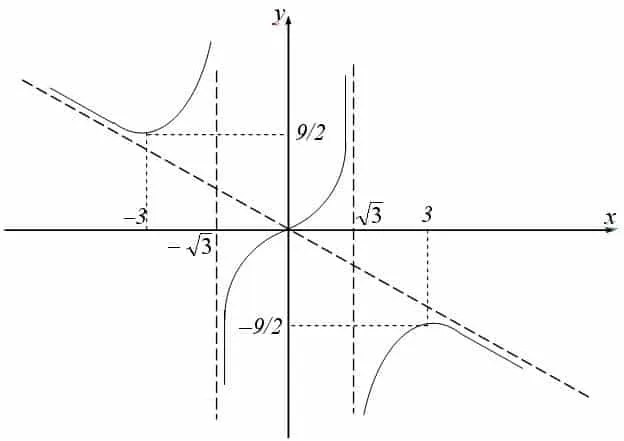
Вычислить производную функции с двумя переменными График функции с использованием экстремумов

Выражение f’₀(x *) = 0 является необходимым условием прекращения функции переменных. Это означает, что первая производная функции должна быть равна нулю в точке x*. Определите точку остановки x, в которой функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной

f₀(x) дважды дифференцируема при x, принадлежащем множеству D. Если условие в точке x* выполняется:.

Если условие выполняется в некоторой точке x*:.

Пример 1. Найти максимальное и минимальное значения функции. В пространстве 1. 3.3.

Ключевым моментом является x.₁ = 2 (f'(x) = 0). Этот пункт относится к разделу 1;3. (Точка x = 0 не является критической, так как она равна 0∉1; 3). Вычислите значение функции в конце отрезка и в критической точке. f (1) = 9, f (2) = 5 /₂, f (3) = 3 8 /₈₁ Ответ: f_мин.= 5 /₂ При x = 2 — f_Макс.= 9 в x = 1

Пример 2. Найти экстремальные значения функции y=x-2sin(x) с помощью производных высшего порядка. Решение. Найдите производную функции: y’= 1-2cos(x). Найдите критические точки: 1-cos(x) = 2, cos(x) = ½, x = ±π/.₃+2πk, k ∈ Z. Найдите и вычислите y’= 2sin(x), x=π/₃+2πk, k ∈ Z является минимумом функции -, поэтому x=—π/₃+2πk, k ∈ Z — точка максимума функции.

Пример 3. Исследуйте экстремальные значения функции в окрестности точки x=0. Решение. Теперь нам нужно найти экстремальное значение функции. Если x = 0 является экстремальным значением, укажите его тип (минимум или максимум). Если x = 0 найти не удается, вычислите значение функции f (x = 0). Заметим, что когда производные по обе стороны от данной точки не меняют своего знака, это не исчерпывает возможных ситуаций даже для дифференцируемых функций: это может произойти для любой малой окрестности по обе стороны от точки x₀ или производная меняет свой знак с каждой стороны. В этих точках экстремальная функция должна быть исследована другими методами.

Пример 4. Число 49 делится на два члена, произведение которых максимально. Решение. Обозначим первый член через x. Тогда (49-x) — это второй член. Произведение максимально: x- (49-x) → максимально или 49x-x 2

Наибольший объем цилиндра

Найдите размеры цилиндра с наибольшим объемом, изготовленного из шарообразного куска радиуса R. Решение: объем цилиндра равен: V = πr2H, где H = 2h, подставим эти значения в целевую функцию.

Найдите экстремальные значения функции V → max. Поскольку функция объема V(h) зависит от одной переменной, используйте онлайн-сервис производных, чтобы найти производную и приравнять ее к нулю. dV /dh=2πR2-6πh2dV/dh=02πR2-6πh2=0 или R2= 3h 2 Из

Второй интервал характеризуется тем, что он не содержит неподвижной точки и не имеет строгих границ. Поэтому невозможно вычислить максимальное или минимальное значение функции. При пределе, установленном на отрицательной бесконечности, и левом аргументе, стремящемся к -3, получается только интервал значений.

Как найти точки минимума и максимума функции

Минимальное и максимальное значения функции, другими словами, экстремумы, — это точки, в которых функция меняет свою монотонность (с возрастающей на убывающую и наоборот). Важно понимать, что экстремумы — это не максимальное и минимальное значения функции. Они символизируются следующим образом:.

• \(y_, y_\) — минимум, максимум функции или экстремумы;
• \(x_, x_\) — точки минимума, максимума функции;
• \(y_, y_\) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

Точка минимума, минимум функции

Точка минимума является точкой\(x_0 \), если существует окрестность всех точек, где неравенство выполняется\(f(x)\ geq f(x_0)\).

Минимальное значение функции — это значение функции для наименьшей точки \(x_0 \)\(x_0)\)

Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до выкидыша). Если вы не можете написать работу самостоятельно, вы можете заказать ее здесь.

Проще говоря, точка минимума — это место, где убывающая функция преобразуется в возрастающую.

Точка максимума, максимум функции

Точка максимума — это точка ˉ(x_0 ˉ), если существует окрестность всех точек неравенства ˉ(f(x)ˉ leq f(x_0)ˉ).

Максимальное значение функции — это значение функции в точке с наибольшим ˉ(x_0 \)ˉ.

Проще говоря, точка максимума — это точка, в которой функция переходит из точки подъема в точку спада.

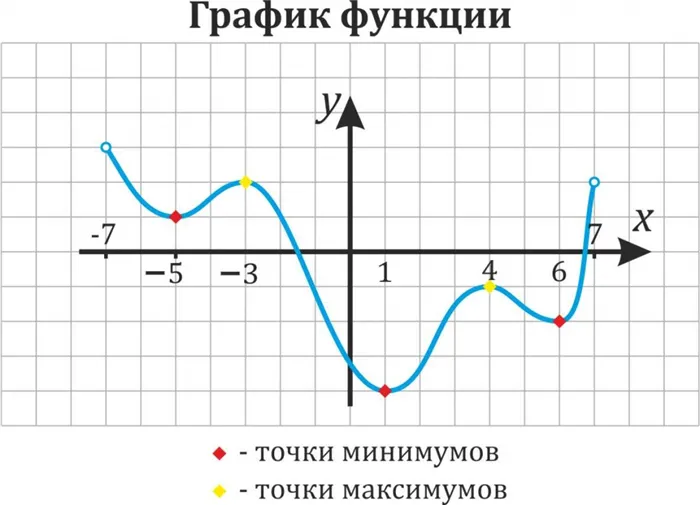
Точки максимума и минимума на графике:.

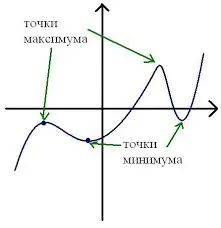
Исследование функций на экстремумы

Теорема. Если функция f (x) является экстремальной в точке ⌘ (x = x_0, ⌘), то ее производная равна нулю или не существует.

Алгоритм поиска экстремумов с помощью производных:.

Найдите поле функции -D (Y).

Определите производную — f ‘(x).

Найдите точку стагнации y = f (x), т.е. точку, принадлежащую d (y), критическую точку, где f ‘ (x) сходится к нулю и производная не существует (например, \(f^, (x) = \ frac1 \), производная не существует при x = 0).

Рассмотрим изменение функции f (x) и знака f ‘ (x) в интервале, где найдена критическая точка (разделите область (функция убывает при отрицательном знаке производной и возрастает при положительном) .

Для каждой критической точки рассмотрите максимальное минимальное значение (возрастающая точка преобразуется в убывающую — максимальное значение — убывающая точка — до минимального значения) или не экстремальное (т.е. если знак производной меняется при прохождении через точку исследования).

Вычислите значение функции в точке экстремума.

Примеры задач

Задача 1

Исследуйте функцию\(f(x)= x^3-3x^2.

Решите задачу в соответствии с алгоритмом:.

(1) Ј(d(y): x \ in(- \ infty;+{ infty)Ј), т.е. x — произвольное число.

3) Из (1) следует, что нет никакого важного момента. Давайте найдем фиксированные:.

Приравняйте f ‘(x) к 0, решите квадратное уравнение \(3x^2-6x = 0 \) и получите \(x_1 = 0 \), \(x_2 = 2. \).

4) Отметьте точки 0 и 2 на горизонтальной оси координат. Пространство \ (- \ Infty; 0)\) для замены x на f ‘(x). Например, x = -1, тогда \(f'(x) = 3^2-6(-1) = 3+6 = 9 \). Существует f ‘(x) > 0. Это означает, что f (x) растет в течение рассматриваемого периода. Аналогичным образом рассмотрите оставшиеся интервалы. Таким образом, в пространстве (0; 2) производная отрицательна и функция убывает, а в пространстве \((2;+\ infty)\) производная правильно возрастает. Это означает, что x = 0 — точка максимального значения, а x = 2 — точка минимума.

5) Найдите значение площади функции.

ОТВЕТ: ǫ (x_ = 2, ǫ; y _ = -4; \ x_ = 0, ǫ y_ = 0 ǫ) или (0; 0) является минимумом функции. (2; -4) является максимальной.

Задача 2

Найдите интервал монотонности функции ǫ (f(x) = \ frac x \).

(3) Таким образом, как и в пункте 1, ключевыми точками являются 2 и -2. Нахождение неподвижной точки приравниванием f ‘(x) к 0 показывает, что уравнение не имеет корней. Следовательно, фиксированной точки не существует. Это означает, что функция является монотонной во всей области определения. Давайте посмотрим, увеличится она или уменьшится. Для этого решите неравенство \(- \ frac^2> \ leq0 \) и вы увидите, что неравенство применимо к каждому x. Другими словами, функция является убывающей.

Помните, что при задании пространства необходимо блокировать важные точки -2 и 2, так как там функция не может быть определена.

Ответ: f(x) Уменьшение в пространстве ɑ

Задача 3

Докажите, что функция \(f(x) = x^5+2x^3-4 \) возрастает на всех арифметических линиях.

(1) ǫ(d(y)): x \ в \ mathbb \). Следовательно, нет никакого важного момента.

3) Приравняйте f ‘(x) к 0 и найдите корень: x =0. Укажите примечание 0 к числу и укажите знак производной в интервалах \(- \ infty; 0)\) и ⌘(0; +⌘)\). Функция возрастает по всему числу, потому что производная принимает положительное значение на обоих интервалах.

Верхняя часть f(x) на участке или в пространстве находится путем исследования функции. План исследования для нахождения максимума на отрезке (или интервале):.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, вы должны сделать то же самое, что и в предыдущем пункте. Найдите, где производная положительна, отрицательна или равна нулю. Чтобы сделать его более понятным, напишите алгоритм с примером решения.

1. Найдите производную функции \(f'(x)\).
2. Найдите корни уравнения \(f'(x)=0\).
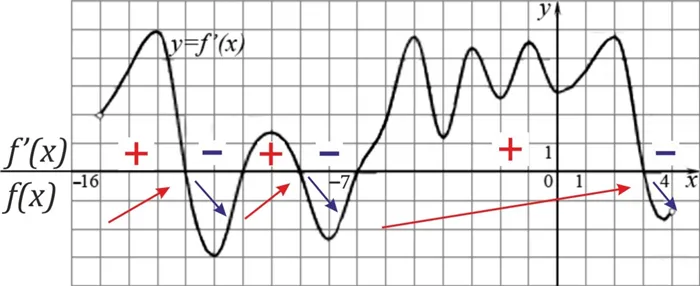
3. Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: — если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума; — если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума; — если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба.

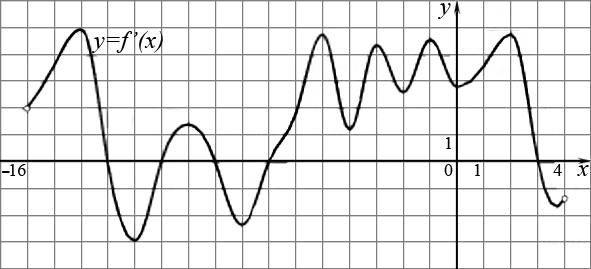
Это! Находятся точки максимума и минимума.

Шкалой можно пренебречь, построив точки на валах, где производная равна нулю. Функциональное поведение может проявляться, как показано на схеме ниже. Таким образом, становится ясно, где находятся максимальные и минимальные значения.

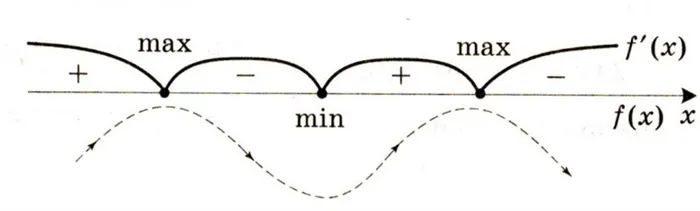
Пример.(Использовать.) Найдите точку максимума функции ǫ (y = 3x^5-20x^3-54 ǫ).Решение:. 1. найти производную функции: ⌘(y ‘= 15x^4-60x^2 \). 2. приравнять к нулю и решить уравнение.

3. -6. Нарисуйте точки на осях чисел и определите, как меняется знак производной и движется функция.

Пример.(Использовать.) Найдите точку максимума функции ǫ (y = 3x^5-20x^3-54 ǫ).Решение:. 1. найти производную функции: ⌘(y ‘= 15x^4-60x^2 \). 2. приравнять к нулю и решить уравнение.

Достаточные условия для существования экстремума функции

Следующее предложение создает экстремальное условие для функции, поскольку ее доказательство отклоняется от темы школьного курса математики и не приведено в нашем пособии.

Утверждение 3. Рассмотрим функцию f (x), непрерывную в пространстве (a, b), с точкой x₀ Эта производная существует во всех частях этого пространства, за исключением, возможно, точки x₀ .

(é). Если для точки выполняется условие:.

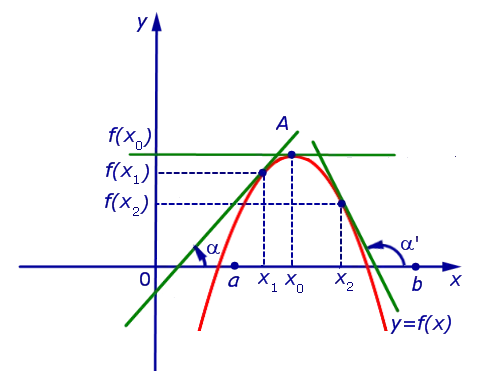
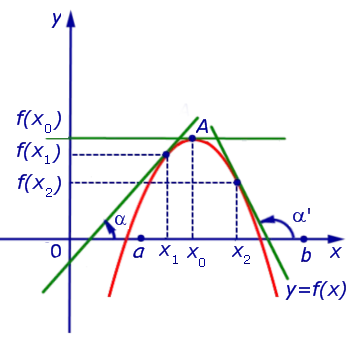
(круг). Если конвенция соблюдена для пункта:.

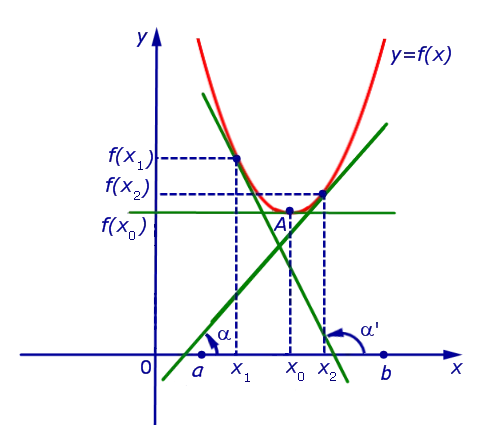
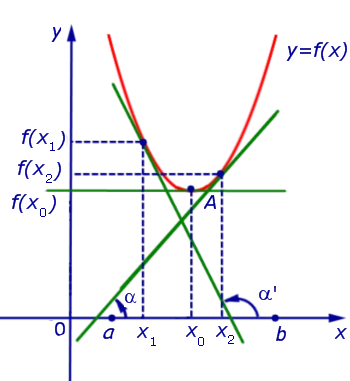
Наблюдение 2. Условия (a) и b) Декларации 3 часто формулируются следующим образом.₀ Производная функции меняет знак с ‘+’ на ‘тогда точка x’₀ Точка максимума функции. При прохождении через точку x₀ Производная функции меняет свой знак с «-» на «+» в точке x₀ Это точка минимального значения функции.

Пример исследования поведения функции

Пример. Нахождение экстремальных периодов роста, сокращения и функционирования

Решение. Сначала найдите интервалы роста, убывания и экстремума функции.

Затем нарисуйте его график. Для этого представьте тип (2) в виде

Анализирует правую часть типа (3) на факторы.

Используйте метод пробелов на схеме.

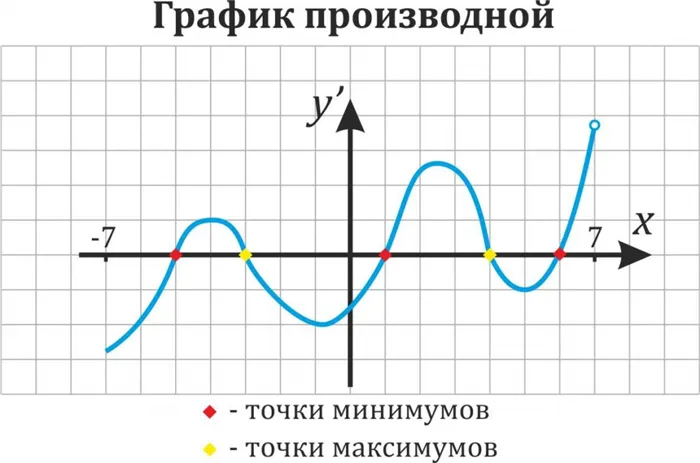
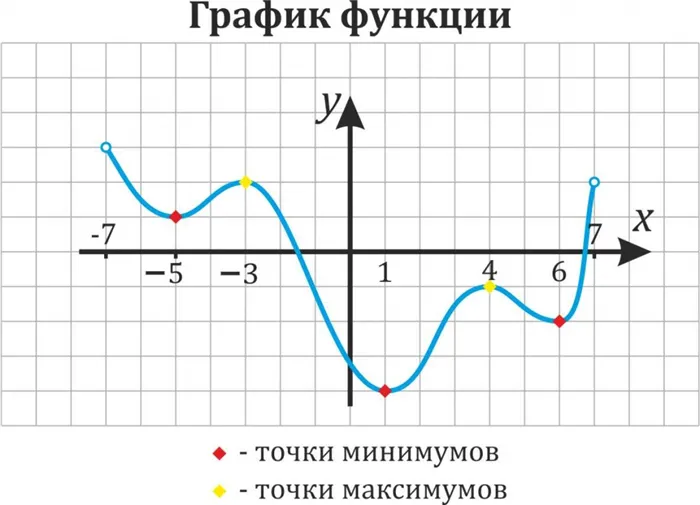
Поскольку решение неравенств.

Тогда, согласно формуле 1, неравенство по функции y₁ с увеличением каждого пространства.

С другой стороны, поскольку решение неравенств

Тогда, согласно формуле 1, неравенство по функции y₁Уменьшение распорок (-2, 0).

Поскольку решение уравнения

x = -2, поэтому производная функции y₁ Измените его знак с «+» на «-» (рис. 8) и, согласно утверждению 3, точка x = -2 является точкой максимума функции y₁, где.

При переходе из точки x = 0 производная функции y₁ Если изменить знак с «-» на «+» (рис. 8), то согласно утверждению 3 точка x = 0 является точкой минимума функции y₁, где.

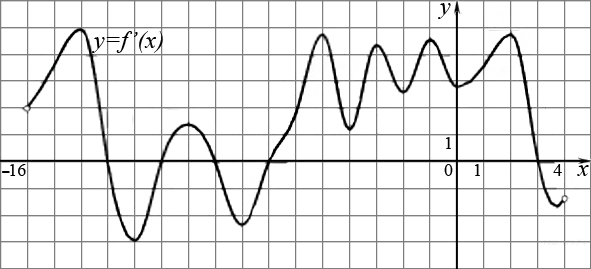
Обратите внимание, что при анализе поведения функции на основе знака ее производной полезно использовать следующий график со стрелками, указывающими на интервалы возрастания и убывания функции (рис. 9).

Исходя из определения модуля упругости, применимо следующее равенство

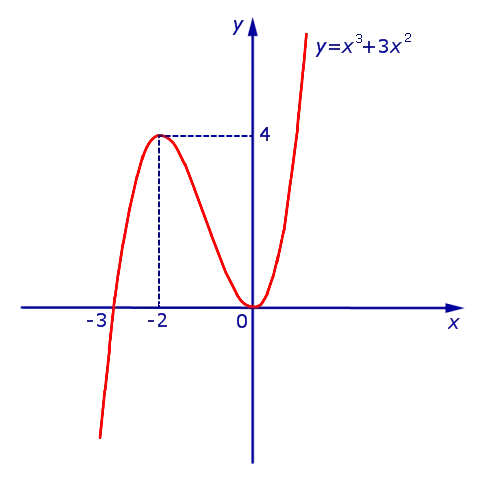
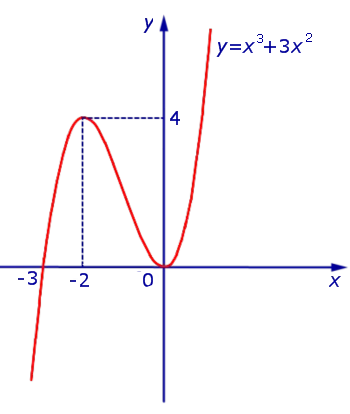
Это равенство имеет место, когда ось кислот симметрична и является частью графика функции y.₁ = x 3 + 3 x 2 (рис. 10), расположенная на нижнем полууровне, оставляя эту часть графика неизменной на верхнем полууровне, функция y = | x 3 + 3 x 2 | (рис. 11).

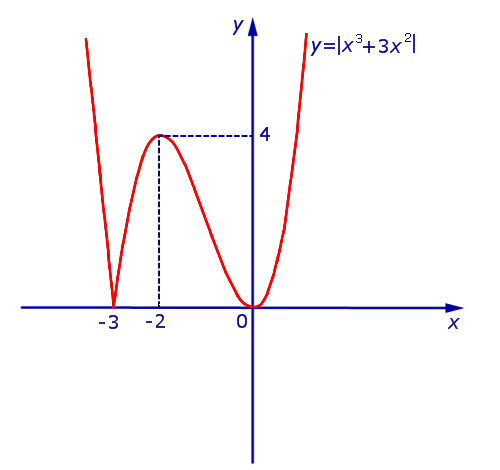
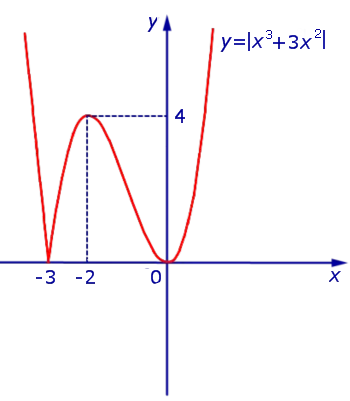
В точке x = -3 не существует производной x 3 + 3 x 2 | функции y = |. На всех остальных участках числовой оси находится функция y = | x 3 + 3 x 2 |.