У кубоида 12 граней, но многие из них одинаковой длины. Поэтому для описания размеров этой формы достаточно всего трех параметров. Обычно их называют длиной, шириной и высотой:
ЭМГеометрия
Фигура, в которой не все точки находятся в плоскости, Фигура, в которой не все точки лежат в плоскости, называется пространственной.
В дополнение к геометрическим твердым телам, пространственные формы также включают в себя двугранные и многогранные углы и другие наборы точек, линий и поверхностей. Основными элементами, составляющими пространственные формы, являются точки и линии, плоскости. Каждая фигура может свободно перемещаться в пространстве, не изменяя своего размера или формы.
Две фигуры считаются одинаковыми, если они могут быть выровнены по всем точкам.
Стереометрия изучает свойства пространственных форм. Две линии в пространстве могут находиться в одном и том же плоскости, и затем либо пересекаются, либо параллельны.
Считается, что две прямые пересекаются, если одна из них не входит ни в одно из бесконечных множеств плоскостей, через другую линию.
Изображение (рисунок или эскиз) пространственной фигуры на плоскости выполнена в соответствии с правилами параллельного проецирования, которые мы также должны знать при чтении чертежа.
(α) Если прямые в пространстве параллельны, то их проекции на чертеже параллельны или одновременны; если прямые на чертеже параллельны, то соответствующие прямые на пространственной фигуре параллельны.
(b) Если линии на чертеже пересекаются, то соответствующие линии в пространстве пересекаются или скрещиваются. При переходе от плоского рисунка пространственной фигуры к ее модели (физической или воображаемой) необходимо научиться уверенно различать пересекающиеся и пересекаемые линии. Без этого невозможно научиться стереометрии.
c) Отношение отрезков параллельных прямых (или прямой) в пространственной фигуре равно отношению их соответствующих отрезков на чертеже. Из этого следует, что в одной группе параллельных сегментов каждый сегмент сокращается один раз при переходе от пространственной фигуры к рисунку, а в другой группе параллельных сегментов другое (но фиксированное для этой группы) количество раз.
г) Углы пространственной фигуры на рисунке обычно меняют свою величину, например, прямой угол пространственной фигуры может быть представлен как острый или тупой. углом.
Невидимые линии пространственной формы представлены на рисунке пунктирными линиями.
Основные свойства плоскости Следующие математические утверждения могут быть выражены следующим образом.
Если две точки лежат на прямой на плоскости, тогда все точки на этой прямой на плоскости.
Если три точки, не лежащие на одной прямой, имеют общую точку. плоскость, притом только одну.
Если две плоскости имеют общую точку, то они имеют общую прямую, проходящую через эту точку, т.е. пересекаются.
Через эту точку и точку, не лежащую на этой прямой, можно провести прямую. плоскость, притом только одну.
Две пересекающиеся линии могут быть проведены с помощью плоскость и только одну.
Две параллельные прямые можно провести через плоскость, притом только одну.
Сегодня мы познакомились с концепцией двугранного угла, мы научились вычислять углы между плоскостями. В качестве особого случая, вместо вычисления угла мы можем просто доказать, что перпендикулярндикулярность плоскостей.
Двугранные углы. Углы между плоскостями. Перпендикулярность плоскостей
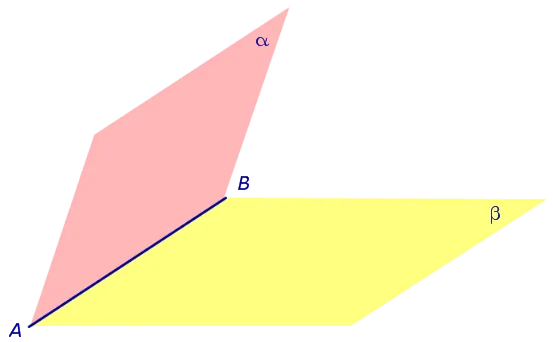
Полуплоскости a и b, которые разграничивают двугранный углы называются гранями двугранного угла и их общее ребро AB называется ребром двугранного угла .
Двугранные углы называют равными двугранными углами, если они могут быть соединены.
На пересечении двух плоскостей образуются четыре двугранных угла (Рисунок 2). Меньший из этих двух углов обычно и называют углом между плоскостями .
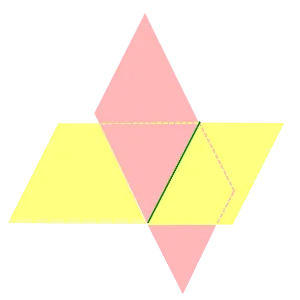
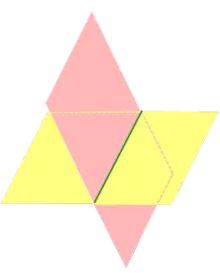
Если на пересечении двух плоскостей формируется из 4 равных двугранных угла, то такие двугранные углы называют прямыми двугранными углами, а сами плоскости называются перпендикулярами. плоскостями (рис. 3).
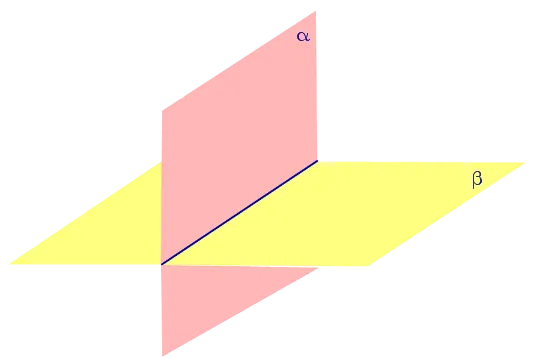
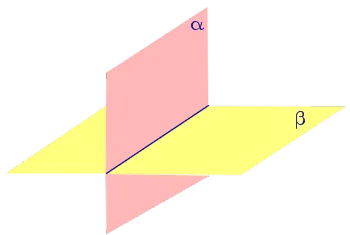
Выберем любую точку C на ребре AB двугранного угла и проведите через него перпендикуляры CD и CE с каждого конца. двугранного угла. Угол DCE, образованный перпендикулярами CD и CE, называется линейным. углом двугранного угла (рис. 4).
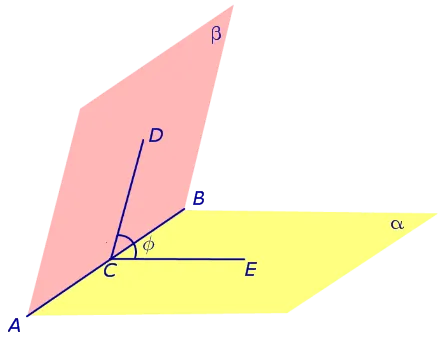
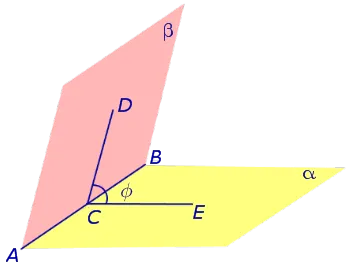
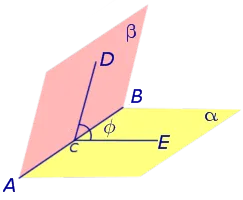
На рисунке 4 угол φ является линейным углом двугранного угла с ребрами a и b и ребром AB .
Линейные углы двугранных углов используются, в частности, для измерения двугранные углы. Например, если линейный угол двугранного угла составляет 30° ( или ), тогда и двугранный угол равен 30° (радиус). Аналогично, если право двугранный угол равен 90° (радиус).
У перпендикулярных плоскостей есть очень интересная особенность: все углы, которые возникли из них, они равны между и равны 90° градусов.
Двугранный угол

Двугранный угол — это часть пространства, которая между двумя полуплоскостями, которые имеют общую границу.

Если в пространстве есть пересечения две плоскости, получаются четыре двугранных угла (аналогично пересечению двух линий, четыре угла). Рассмотрим один из них.

Выберем любую точку \(a\) двугранного угла любую точку \(C\) и проведите две пересекающиеся прямые AC &below; a и BC &below; a, и через эти прямые проведите — плоскость c под прямым углом к краю \(a\).
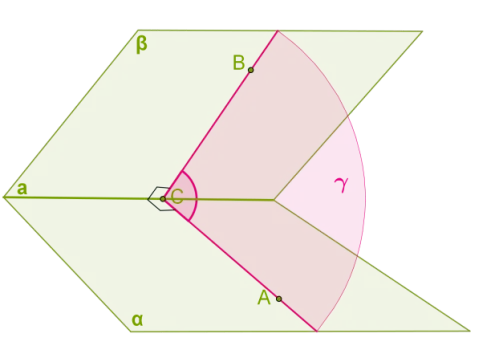
Проведите биссектрису пересекающихся линий \(AC\) и \(BC\).плоскостей α и β с плоскостью γ образовывать угол ∡ ACB. Этот угол называется линейным углом углом двугранного угла. Величина линейного угла не зависит от выбора точки \(C\) на ребре \(a\).
Если на перекрестке плоскостей один из двугранных углов \(90°\), то остальные три — это угла — тоже \(90°\). Эти плоскости называются прямоугольными.
1. если один из двух плоскостей проходит через линию, которая перпендикулярна другой линии плоскости, то такие плоскости перпендикулярны.
2. плоскость, перпендикулярная прямой, на которой пересекаются две прямые. две плоскости, перпендикулярно каждому из них. плоскостей.
3. Если две плоскости перпендикулярны и в одном из них прямая перпендикулярна линии пересечения плоскостей, тогда эта линия перпендикулярна второй линии плоскости.
Мы хотим представить несколько лучей в пространстве с общим началом координат. Они также могут быть представлены как часть пересекающихся линий. плоскостей — три, четыре или больше — и мы называем их гранями многогранника. угла.
У перпендикулярных плоскостей есть очень интересная особенность: все углы, которые возникли из них, они равны между и равны 90° градусов.
Если в плоскости Постройте две пересекающиеся прямые AK и BN в точке M, то плоскость Разделите их на 4 региона, сформировав 4 «плоских» региона. » угла.
Аналогично, две пересекающиеся прямые являются плоскости c и b от линии AB, разделите пространство на 4 области, образуя 4 двугранных угла.
Определение. Двугранный угол — это фигура, образованная линией AB и двумя полуокружностями, которые не принадлежат друг другу.плоскостями с общей границей AB, которые не принадлежат к плоскости.
Полуплоскости, образующие двугранный углы называются площадями. двугранного угла .
Линия AB (граница половинного угла) является общей для всех поверхностей.плоскостей) называется ребром двугранного угла .
Обозначение: KABL, где K и L — позиции, принадлежащие разным поверхностям, а AB — ребро. двугранного угла.
- стена комнаты с полом или потолком;
- двускатная крыша;
- полураскрытая книга;
- открытка со сгибом.


Измерение двугранных углов ограничивается измерением линейного углов. Определение. Линейный углом двугранного угла это плоский угол, образованный двумя лучами, перпендикулярными к граням данной точки. двугранного угла и перпендикулярно его краю.
Все линейные углы данного двугранного угла равны между собой.
За величину двугранного угла Он принимает значение своего линейного угла. Выражение двугранный угол, равный ᵠ, означает, что значение соответствующего линейного угла равна ᵠ .
Плоский угол называется прямым (острым, тупым), если он равен 90° (меньше 90°, больше 90°).
Выберем любую точку \(a\) двугранного угла любую точку \(C\) и проведите две пересекающиеся прямые AC &below; a и BC &below; a, и через эти прямые проведите — плоскость c под прямым углом к краю \(a\).
Как найти двугранный угол
Угол с двумя поверхностями — это участок пространства, образованный между двумя полуплоскостями, которые имеют общую границу.
Полуплоскости и, образующие двугранный Углы называются гранями (рис. 3.6.1). Общая линия этих граней называется ребром. двугранного угла. Возьмем точки и на ребре. двугранного угла. Плоский угол обозначается двумя буквами: Угол Иногда двугранный обозначается четырьмя буквами, из которых две средние буквы обозначают точки на краях, а две крайние — точки на гранях. Пусть, (рис. 3.6.1), тогда двугранный обозначается следующим образом: Угол Выберем произвольную точку на краю двугранного угла произвольной точки и по нее плоскость перпендикулярно к краю (рис. 3.6.2). Плоскость пересекает края двугранного угла из линий и, образующих угол. Этот угол называется линейным углом. углом двугранного угла. Легко показать, что значение линейного угла угла не зависит от выбора точки края. На краю возьмем точку, отличную от, и проведем через. нее плоскость. Пусть плоскость пересекает грани двугранного угла Поэтому, согласно теореме о следе, значения, приведенные в разд. углы равны. Величина двугранного угла равна значению линейного угла. Если – величина двугранного угла, то .
На пересечении двух плоскостей образуются четыре двугранных угла. величина меньшего из двух двугранных углов называется углом между этими плоскостями .
Если плоскости параллельны, угол между равны по определению. Если — величина угла между двумя плоскостями, то .








