3. взять одно из основных свойств дробейУмножьте делимое и делитель на дополнительный коэффициент. После умножения делитель должен быть равен наименьшему общему кратному, вычисленному ранее. Затем мы можем продолжить к сложению.
Сложение дробей.
Разные действия с дробями мы можем, например, сложение дробей. Сложение дробей можно разделить на несколько видов. Каждый тип имеет сложения дробей имеет свои собственные правила и алгоритмы. Давайте посмотрим надробно каждый вид сложения.
Давайте рассмотрим пример, чтобы увидеть, как дроби с общим знаменателем.
Пешие туристы прошли из пункта А в пункт Е. В первый день они прошли пешком от точки А до точки Б или \(\frac\) все расстояние. На второй день они прошли от точки B до точки D, или \(\frac\) всего маршрута. Какое расстояние они прошли от начала тропы до точки D?
Чтобы определить расстояние от точки A до точки D, нужно сделать следующее сложить дроби \(\frac + \frac\).
Сложение дробей с одинаковыми Дело в том, что знаменатели этих дробей сложить, а знаменатель остается прежним.
В алфавитном порядке сумма дробей с одинаковыми знаменателей имеют следующий вид:
Ответ заключается в том, что ходоки прошли весь путь пешком.
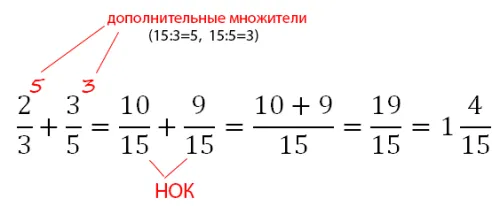
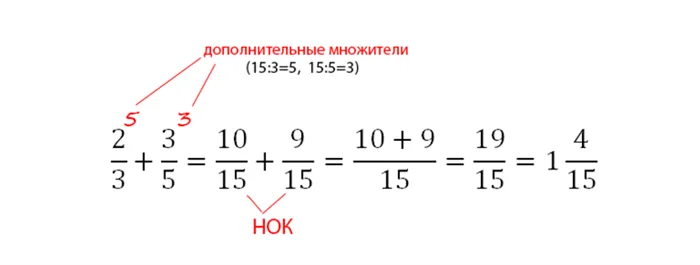
Сложение дробей с разными знаменателями.
Нужно сложить две дроби \(\frac\) и \(\frac\).
Чтобы сложить дроби Если знаменатели разные, мы должны сначала найти общий знаменатель, а затем найти сложения дробей с одинаковыми знаменатели.
Для знаменателей 4 и 7 общий знаменатель равен 28. Первый дробь \(\frac\) нужно умножить на 7. Второе. дробь \(\frac\) нужно умножить на 4.
В алфавитном порядке мы имеем следующую формулу:
Сложение смешанных чисел или смешанных дробей.
Сложение смешанных дробей \(\frac\) это по закону. сложения.
У смешанных дробей мы складываем целые числа с целыми числами. и дробные части с дробными.
Если дробныЧасти смешанных чисел имеют одинаковые знаменателя мы складываем числители, а знаменатель остается прежним.
Давайте сложим смешанные числа \(3\frac\) и \(1\frac\).
Если дробныЕсли части смешанных чисел имеют разные знаменатели, мы находим общий знаменатель.
Выполним сложение смешанных чисел \(7{frac\) и \(2{frac\).
Знаменатели разные, поэтому нам нужно найти общий знаменатель, равный 24. Давайте умножим первое дробь \(7{frac}) дополнительно в 3 раза, а второй дробь \(2\frac\) на 4.
Вопросы по этой теме: Как добавить дроби? Ответ: сначала определите тип выражения: у дробей одинаковые Знаменатель, разные знаменатели или смешанные знаменатели. дроби. В зависимости от типа выражения переключитесь на алгоритм решения.
Как решать дроби С разными знаменателями? Ответ: Найдите общий знаменатель, а затем следуйте правилу. сложения дробей с одинаковыми знаменатели.
Как вы решаете смешанные дроби? Ответ: Добавьте целые числа к целым числам. и дробные части с дробными.
Пример 1: Может ли сумма двух правильных целых чисел равняться одному и тому же числу целых чисел? дробей Может ли сумма двух правильных чисел дать правильное число? дробь? Неправильную дробь? Приведите примеры.
Дробь \(\frac\) является действительной дробью. дробь, ½ — это результат сложения двух действительных дробей. дробей \(\frac\) и \(\frac\).
Дробь \(\frac) является ложной дробью дроби, сумма правильных дробей дробей \(\frac\) и \(\frac\).
Ответ на оба вопроса — да.
Пример №2: Добавить дробиa) \(\frac + \frac\) b) \(\frac + \frac\).
Пример #3: Напишите смешанный дробь как сумма натурального числа и соответствующего дроби(a) \(1\frac\) (b) \(5\frac\).
Пример #4: Вычислите сумму: (a) \(8{frac + 2{frac}) b) \(2frac + \frac\) c) \(7frac + 3frac)
(a) \(8{frac + 2{frac} = (8 + 2) + (\frac + \frac) = 10 + \frac = 10\frac)
Задача 1: В обед они съели \(\frac\) пирожного, а вечером съели \(\frac\) пирожного. Как вы думаете, торт полностью съеден или нет?
Решение: Знаменатель дроби равно 11 и показывает, на сколько частей был разделен торт. За обедом было съедено 8 из 11 кусков торта. За ужином из 11 кусков торта было съедено 3. Добавьте 8 + 3 = 11, поэтому они съели 11 кусков торта, что составляет целый торт.
Ответ: Весь торт был съеден.
You may also like:

Десятичные дроби. Деление и дробь десятичных чисел дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Складываем дробные части с одинаковыми знаменателями, помня, что нас интересует только числитель, знаменатель остается таким, как был: \(\over>+\over>=\over>\)
Сложение дробей с разными знаменателями.
Правила сложения дробей с разными знаменателями:
- приводим дроби к наименьшему общему знаменателю (НОЗ). Для этого находим наименьшееобщее кратное (НОК) знаменателей;
- складываем числители дробей, а знаменатели оставляем не меняя;
- сокращаем дробь, которую получили;
- если получили неправильная дробь — Преобразование неровностей дробь в смешанную дробь.
Примеры сложения дробей с разными знаменателями:
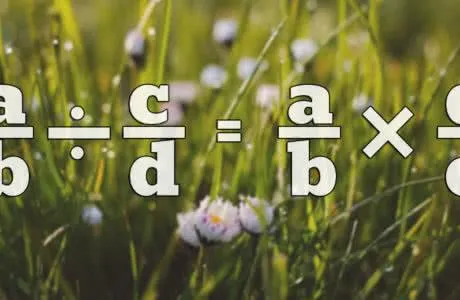
Сложение смешанных чисел (смешанных дробей).
Правила сложения смешанных дробей:
- приводим дробные части этих чисел к наименьшему общему знаменателю (НОЗ);
- отдельно складываем целые части и отдельно дробные части, складываем результаты;
- если при сложении дробныx неравномерно извлеченная часть дробь, извлекает из него целочисленную часть дроби и прибавляем ее к полученной целой части;
- сокращаем полученную дробь.
Пример сложения смешанной дроби :
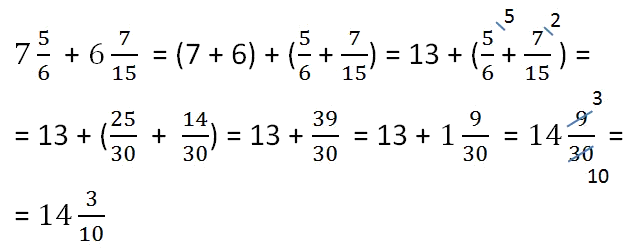
Сложение десятичных дробей.
При сложении десятичных дробей Процедура записывается «столбиком» (как обычное умножение в столбик), так что одинаковые цифры стоят друг под другом без сдвига. Запятые должны стоять четко друг под другом.
Правила сложения десятичных дробей:
При необходимости уравняйте количество знаков после запятой. Для этого добавьте нули к нужному количеству цифр. дроби.
2. Записываем дроби так, чтобы запятые находились друг под другом.
3. Складываем дроби, Не обращая внимания на десятичную точку.
4. поставьте запятую под запятыми в сумме, дробей, которые мы добавляем.
Примечание. Когда даются десятичные числа, они дробей имеют разное количество знаков после запятой к дроби, в котором меньше десятичных знаков, мы добавляем нужное количество нулей, чтобы получить уравнение в дробях количество цифр после десятичной точки.
Давайте рассмотрим пример. Вычисление суммы десятичных знаков дробей:
Баланс количества знаков после запятой дробях. Добавьте 2 нуля к правой части десятичного числа. дроби 13,7 .
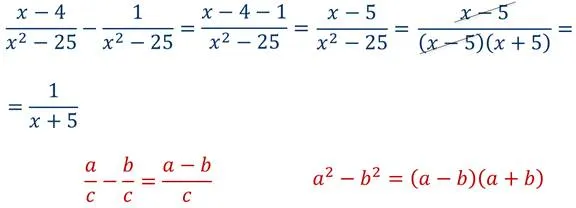
Если сложение десятичных дробей Вы выучили его достаточно хорошо, вы можете заполнить недостающие нули в своей голове.
Складываем дробные части с одинаковыми знаменателями, помня, что нас интересует только числитель, знаменатель остается таким, как был: \(\over>+\over>=\over>\)
Сложение и вычитание дробей с одинаковыми Знаменатель
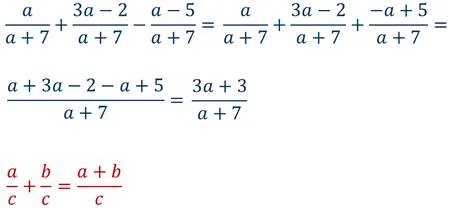
В этом уроке мы углубим ваше понимание логических выражений. Мы продолжим развивать идеи преобразования логических выражений. Мы введем правило сложения и вычитание логических выражений. дробей с одинаковыми знаменатели.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный кабинет, купив его в каталоге.


Конспект урока «Сложение и вычитание дробей с одинаковыми знаменателями»
Вы уже знаете, как логически складывать и вычитать. дроби с одинаковыми Знаменатель. Давайте вспомним правила сложения и вычитания простых людей дроби.
Чтобы сложить дроби с одинаковыми Знаменатель, нужно сложить сайт числитель и знаменатель остаются неизменными.
Чтобы из одной дроби вычесть другую дробь с таким же знаменателем мы должны добавить числитель уменьшительно-ласкательное вычитание числитель вычитаемого и знаменатель остаются неизменными.
В алфавитном порядке эти правила можно записать следующим образом:
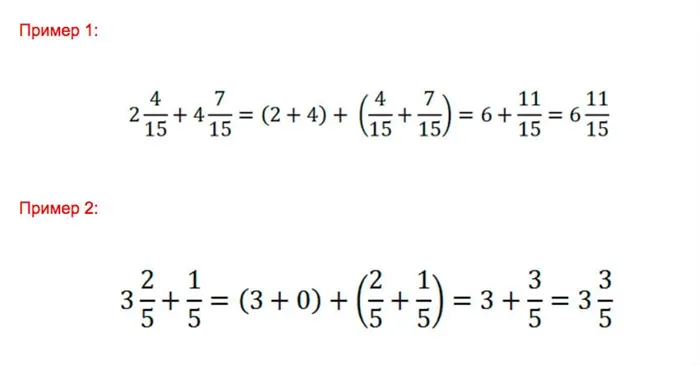
Эти уравнения являются тождествами, поскольку они справедливы при любых значениях переменных a, b и c, кроме случая, когда tse равно нулю.
Доказательство

Поэтому добавьте любой рациональный дроби с одинаковыми знаменателями.
Правило сложения рациональных дробей с одинаковыми знаменатели :
Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить числители, а знаменатель оставить прежним.
Мы можем сформулировать это правило в алфавитном порядке следующим образом:

Это правило действует при сложении любого числа дробей.
Пример 1. Найдите сумму дробей.

Пример 2: Найдите сумму. дробей.

Пример 3: Найти сумму. дробей.
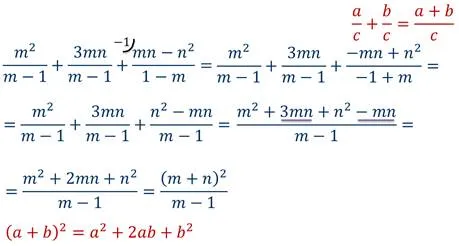
Вычитание логических дробей с одинаковыми Знаменатель выполняется аналогично сложению.
Правило логического вычитания дробей с одинаковыми от знаменателей
Для удаления рациональных знаменателей дробей с одинаковыми Вычтите знаменатели из числителя первого числа. дроби вычесть числитель второго дроби, а знаменатель остается прежним.
Мы можем сформулировать это правило в алфавитном порядке следующим образом:

Пример 4: Найти разность дробей.
Пример 5: Найти разность дробей.
В повседневной жизни, когда мы делим целый объект на части, мы на самом деле имеем дело с долями или дробями. Математика занимается не конкретными объектами, а их числовым выражением. Число также можно разделить на дроби, и каждая дробь является дробью.
Как найти наименьшее общее кратное, наименьший общий знаменатель (НОК или НОЗ)
Наименьшее общее кратное двух чисел (наименьший общий знаменатель) (НОМ) — это наименьшее натуральное число, которое делится на оба числа без остатка.
Иногда НОК можно найти в голове, обычно путем перемножения двух знаменателей. Затем два знаменателя делятся друг на друга.
Однако для больших чисел возникают проблемы, и нам приходится находить НОК в письменном виде, используя следующий алгоритм:
Чтобы найти NOC различных номеров, необходимо:
Проанализируйте эти числа на простые множители Возьмите наибольшее разрешение и запишите эти числа в виде произведения. Выберите числа в других разрешениях, которые не встречаются (или встречаются реже) в самом большом разрешении, и добавьте их к произведению.
Умножьте все числа на произведение, которое является НОК. Например, найдите НОК 28 и 21:
Нерегулярное произведение — это произведение, в котором числитель больше знаменателя. дробь, Когда числитель больше или равен знаменателю. Например, 21/4. Такое число смешивается и читается как пять целых четвертей и записывается как 5 1/4.
Сокращение дробей
Приведение дробей в общем знаменателе иногда делает его громоздким. В таком случае можно дробей, т.е. числитель и знаменатель делятся на общий делитель.

Например \(\over>\), общий делитель равен 3, мы уменьшаем дробь, делим числитель и знаменатель на 3, получаем: \(\over>=\over>\)
Например \(\over>\), общий делитель равен 8.
Вы видели правила. сложения дробей понятны и несложны. Теперь вы можете не только проверить домашнее задание вашего ребенка, но и сказать ему, в каком порядке он должен его выполнять. сложение разных дробей Правильно. И ваш ученик не раз скажет: «Математика». сложение дробей — Все очень просто!








