В этом курсе вы узнаете о замечательном числе (числах), которое нельзя записать цифрами. Вы узнаете о. Сформируйте представление о длине окружности. Извлечение типов длины окружности. Узнайте, как использовать типы длины цикла для решения задач.
Длина окружности
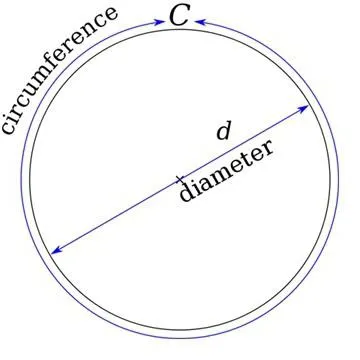
Напишите тип и вычислите длину окружности через ее диаметр. Формула выглядит так: C = PD, где C — окружность, а D — диаметр круга. Это означает, что окружность цикла равна произведению диаметров чисел II (пи приблизительно равно 3,14). X Источники.
Обменяйте значения, данные в прессе, и найдите окружность круга. X-источники.
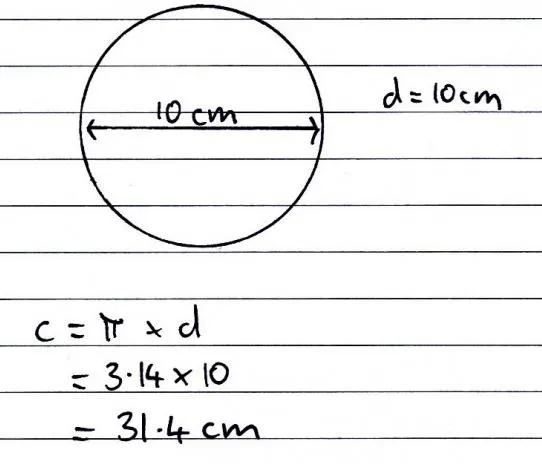
- Пример: у вас есть круглый бассейн диаметром 8 м, и вы хотите поставить вокруг него забор на расстоянии 6 м. Чтобы рассчитать длину забора, сначала найдите диаметр окружности, то есть диаметр бассейна плюс расстояние до забора с обеих сторон. В нашем примере диаметр равен 8 + 6 + 6 = 20 м. Подставьте это значение в формулу.
- C = πd
- C = π x 20
- C = 62,8 м
Напишите тип и вычислите длину окружности через радиус. Радиус равен половине диаметра, каждый диаметр — это два луча (2R). Тогда формула имеет вид C= 2PR, где C — окружность, а r — радиус круга. Это означает, что длина окружности равна удвоенному произведению радиусов чисел II (π приблизительно равно 3,14). X Источники.
Обменяйте данные значения по типу и найдите длину окружности. Например, отрежьте полоску декоративной бумаги и красиво оберните ею кекс при подаче. Радиус кекса равен 5 см. Замените это значение на тип. X Источники.
- Можете купить инженерный или научный калькулятор, в котором уже есть кнопка π. Так вам придется нажимать меньше кнопок, к тому же ответ будет более точным, поскольку встроенная кнопка π имеет более точное значение, чем 3,14.
- Чтобы вычислить окружность, зная диаметр, просто умножьте диаметр на число пи.
- Радиус всегда равен половине диаметра.
- При решении задачи от вас могут потребовать писать не значок π, а его числовое значение — 3,14 (или с большим количеством знаков после запятой). Уточняйте требования у учителя.
- Если вы не можете решить задачу, попросите помощи у друзей, членов семьи или учителя. Они всегда помогут!
- Не забывайте перепроверять вычисления, так как одна ошибка приведет к неправильному результату.
- Не торопитесь. Помните старую пословицу — семь раз отмерь, один раз отрежь.
Что такое окружность и где она встречается?
Эта плоская фигура имеет множество точек, равных другой точке, которая является центром. Это расстояние называется радиусом.
В повседневной жизни вычисление длины окружности требуется нечасто, разве что инженерам и конструкторам. Например, они создают конструкции механизмов, в которых используются шестерни, порты и колеса. Архитекторы создают дома с круглыми или арочными окнами.
Каждый из этих случаев требует иной степени точности, чем другой. И невозможно очень точно рассчитать длину окружности. Это связано с бесконечным характером первого числа в уравнении. ‘PI все еще завершен. В большинстве случаев используются округленные значения. Степень точности выбирается так, чтобы дать наиболее правильный ответ.
Примеры заданий
Допущения. Найдите длину окружности с радиусом 5 см.
Решение. Вычислить эту площадь очень просто и сразу. Все, что вам нужно сделать, это использовать первый тип. Пока известен радиус, достаточно обменяться ценами и рассчитать 2, умноженное на радиус 5 см, дает 10.
Тон. Дано колесо, его окружность известна и равна 1256 мм. Необходимо рассчитать его радиус.
Решение. Для решения этой задачи необходимо использовать один и тот же тип. Однако только известные длины нужно делить на произведение 2 и P. Произведение дает результат: 6,28. После деления оставшееся число равно 200. Это та ценность, которую вы ищете.
Тон. Если известно, что окружность равна 56,52 см, вычислите диаметр.
Решение. Аналогично предыдущей задаче, разделите известную длину на p-значение, округленное до ближайшего сантиметра. Результатом этого закона является число 18. Возникает результат.
Тон. Длины индикаторов часов равны 3 см и 5 см. Необходимо рассчитать длину окружности, представляющей конец.
Разрешение. Первый тип необходим, поскольку индикаторы совпадают с лучами окружности. Его необходимо использовать дважды.
Для первой длины произведение состоит из множителей 2, 3.14 и 3. Результат — 18,84 см.
Для второго ответа умножьте на 2, p и 5. В результате получается число 31,4 см.
Тон. Белка бежит в колесе с двумя цифрами. Каково расстояние за полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому необходимо использовать соответствующий тип. Другими словами, умножьте значение p на 2 m. Расчет дает результат: 6,28 м.
ОТВЕТ: белка пробегает 6,28 м.
Объясните, как можно иметь конечные значения, если периметр можно разделить на отрезки, и если эти отрезки можно разделить еще на меньшие отрезки, и т.д. Как это можно построить, будучи конечным в бесконечном числе частей?
Длина окружности

В этом курсе вы узнаете о замечательном числе (числах), которое нельзя записать цифрами. Вы узнаете о. Сформируйте представление о длине окружности. Извлечение типов длины окружности. Узнайте, как использовать типы длины цикла для решения задач.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеокурсам, вам нужно быть в списке, чтобы купить их и добавить в свой личный гардероб.
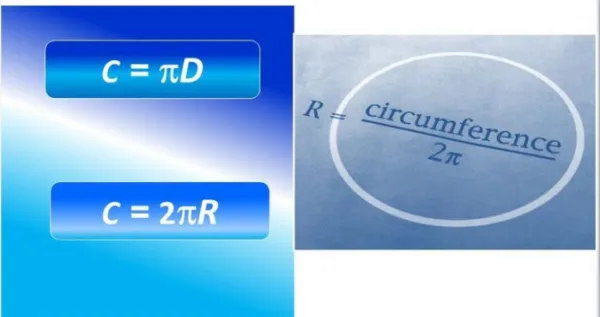


Конспект урока «Длина окружности»
На этом уроке мы познакомимся с числом
В 5 классе была представлена большая линейка окружностей и их элементов. Вы, конечно, уже научились проектировать круг компаса.
Однако такие инструменты, как компас, не всегда присутствовали в нашей жизни. Как вы думаете, можно ли сконструировать велосипед без компаса? Конечно, мы можем!
Давайте попробуем провести небольшой эксперимент. Возьмите монету, положите ее на лист бумаги и обведите контур валюты карандашом.

Смотрите, на листе есть след. Что это за форма? Да! Это круг! С помощью линейки можно измерить диаметр.
Диаметр валюты составляет 5,5 см.
Скажите, можете ли вы измерить длительность самого цикла? Потому что к нему нельзя приложить линейку.
Но мы можем сделать кое-что еще. Возьмите нитку и оберните ее вокруг монеты, затем обрежьте эту нитку и измерьте ее линейкой, чтобы получить длину круга. Сделайте это с монетой.

Окружность монеты составляет 17,27 см.
Чтобы получить представление об окружности, возьмите проволочное кольцо, разрежьте его и согните проволоку. Полученная проволока — это длина окружности.
Вы можете заметить, что длина нити примерно в три раза больше диаметра монеты.
Обозначим длину окружности буквой С, а её диаметр буквой D. Оказывается, какую бы окружность мы ни взяли, частное от деления С на D всегда одно и то же. Сначала было замечено, что длина любой окружности примерно в 3 раза больше диаметра. Затем этот результат был уточнен – в
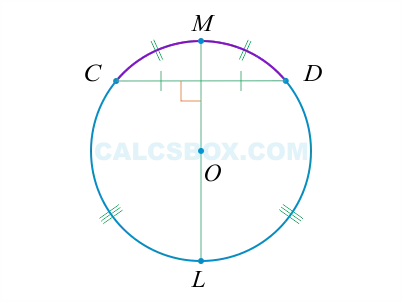
(Чтобы избежать проблем при записи вычислений, древнегреческие математики стали обозначать его греческой буквой p — первоначальной буквой греческого boundary, означающей «граница»).
Было доказано, что число
Можно написать приблизительную стоимость миллионов миллиардера. Поэтому тип используется в формуле, а его приблизительное значение применяется для практических расчетов.
Причина того, что длина окружности до длины ее диаметра — одно и то же число в каждом цикле.
Если C обозначает длину окружности, а D — диаметр, то существует

Обычно принято писать тип длины цикла в радиусе
Обратите внимание, что это число является причиной длины диаметра длины окружности.
В Лондоне была построена самая большая в мире часовая башня, которая имеет название Биг-Бен. Длина диаметра циферблата часов на башне равна 7 метров. Определите длину окружности часов, если число

Минутная стрелка описывает окружность длиной 18 см. Определите длину минутной стрелки, если число

Спортсмен пробежал расстояние 42000 м, причём сделал полных 105 об
Пример: найти длину окружности. Его диаметр составляет 6 см. Используйте вышеуказанный тип по кругу. Сначала нужно найти радиус. Для этого разделите диаметр 6 см на 2, чтобы получить радиус цикла 3 см.
Длина окружности
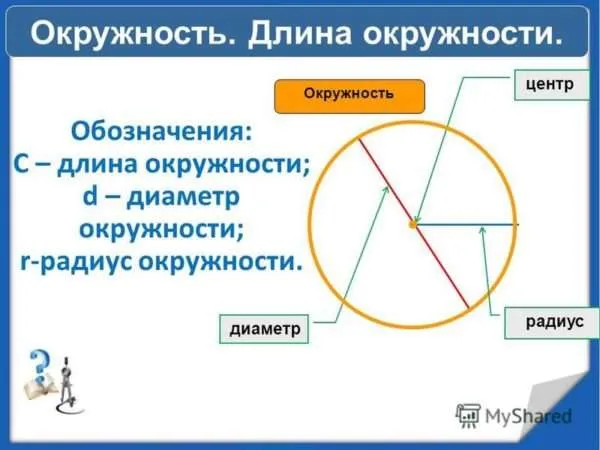
Здравствуйте, уважаемые читатели блога ktonanovenkogo.ru. Сегодня у нас еще один предмет по математике. Его преподавали в шестом классе. Она называется длиной окружности.
Это важный размер для решения многих проблем включая единые государственные экзамены.
Поэтому наша статья очень полезна для старшеклассников. А для всех остальных это веская причина обновить свои знания.
Что такое окружность
Но сначала напомним, что называется кругом.
Круг — это кривая, замкнутая линия, состоящая из множества точек. И все эти точки находятся на одинаковом расстоянии от центра окружности.
Определение немного «тяжеловато», но это официальная формулировка, которая приводится в школьных учебниках. Графика выглядит намного проще.
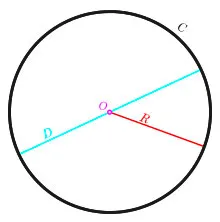
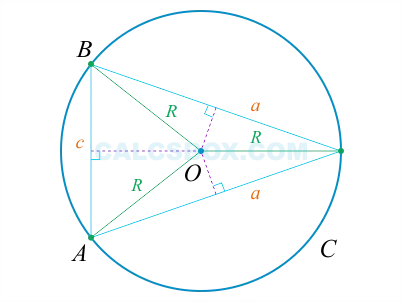
Ниже приведен пример окружности, где все точки кривой «c» находятся на равных расстояниях от центра «o».
Кстати, расстояние от центра до края окружности называется радиусом и обозначается буквой R.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, является диаметром d. Как всем известно, диаметр — это два дополнительных луча (d = 2R).
Интересный факт! Точка каким-то образом является окружностью. В математике это называется «цикл нулевого радиуса».
Для проектирования нормального цикла необходимо использовать специальный инструмент — компас. Можно также нарисовать круг нужного радиуса.

Длина окружности через диаметр
Почему вы так много говорили о его окружности, радиусе и диаметре? Все просто — их нельзя разделить при вычислении окружности круга.
Эта взаимосвязь была замечена еще древними египтянами. Математики того времени были очень продвинуты в различных механических расчетах. Этого достаточно, чтобы напомнить нам, насколько надежно были построены пирамиды. Им более 5 000 лет, и, похоже, они следуют тому же или даже большему.

Таким образом, египтяне обнаружили, что отношение периметра к диаметру круга является стабильной величиной.
Другими словами, если взять круги совершенно разных размеров, а затем разделить их длину на диаметр, то получится одно и то же число.
У египтян было число три, но с более точным значением. Получилось 22/7, или три целых числа и 1/7.
Так появилась математическая константа «PI». В настоящее время она является одним из столпов науки и решает множество проблем.
Кстати, название «P» происходит от греческого слова «domain», которое переводится как круг. Граница» — это диаметр.
Именно такие названия использовал математик Леонгард Эйлер, когда в 1737 году представил научному сообществу числа PI, используя буквы вышеприведенных слов.
Сегодня каждый ученик знает, что ПМ равен 3,14. Это считается базовой ценой, но на самом деле это бесконечное количество десятичных цифр.

Угол, находящийся над окружностью и расположенный между двумя секущими, равен половине разности между значениями углов дуги окружности угла.
Полезное видео: длина окружности
Такие проблемы чаще всего решают инженеры и архитекторы, но нужный тип знаний полезен и в повседневной жизни. Например, вам нужно обернуть полоску бумаги вокруг торта, выпеченного в поперечнике 20 см. Затем можно легко определить длину полосы.
Другой пример: вы хотите построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна составляет 10 м, а ограждение необходимо установить на расстоянии 3 м, то результирующий цикл R составит 13 м. Длина в этом случае будет следующей.
L = 2PR = 2 * 3,14 * 13 = 81,68 м.
Определение немного «тяжеловато», но это официальная формулировка, которая приводится в школьных учебниках. Графика выглядит намного проще.
Вписанная окружность
Зарегистрированная окружность — это окружность, касающаяся стороны многоугольника.
Она сосредоточена в месте пересечения биссектрис углов многоугольника.
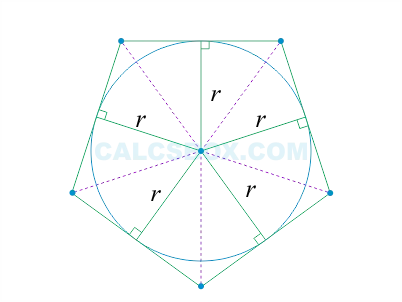
Не все многоугольники могут быть зарегистрированы в круге.
Площадь многоугольника с циклом регистрации задается типом
\ p \ — половина границы многоугольника.
\ \ \ \ \} — радиус внутри клетки.
Предполагается, что радиусы в ячейках равны.
Если окружность зарегистрирована как выпуклый четырехугольник, то определяется сумма противоположных длин. И наоборот, если сумма противоположных длин одинакова, то круг регистрируется в выпуклом четырехугольнике.
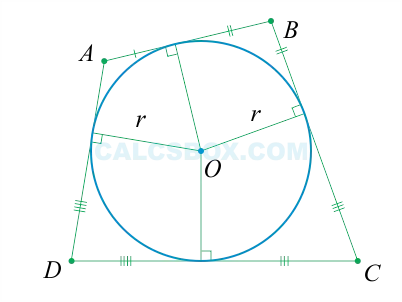
Можно зарегистрировать круг в любом из треугольников. Только один. В точке, где найден внутренний угол, находится центр в клетке.
Радиус академика рассчитывается с использованием следующих типов

Описанная окружность
Если окружность проходит через все вершины многоугольника, она называется периметром вокруг многоугольника.
Середина вертикального пересечения является центром периметра.
Радиус можно найти, вычислив его как радиус окружности, описанной вокруг треугольника, заданного тремя вершинами многоугольника.
Есть одно условие. Граница вокруг четырехугольника может быть описана только в том случае, если сумма противоположных углов равна ⌘(180^.< \circ>(\).
)
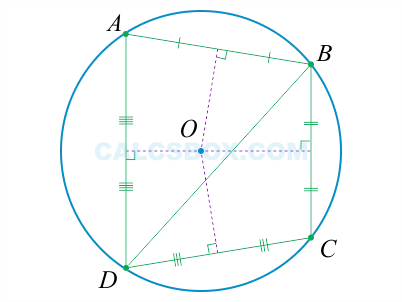
На треугольнике можно сформировать круг и только один круг. Центром такой окружности является точка пересечения вертикальных средних треугольников.
Периферийные лучи могут быть рассчитаны в соответствии с типами.
\(a \), ⌘(b \) и ⌘(c) — длины сторон треугольника, the