Уже в пятой начальной школе математика показывает, что дроби связаны с процентами. Верно: процент — это один сантиметр от любого числа, обозначается символом %.
Десятичные дроби. Понятие десятичной дроби
Дробные числа можно представить в виде десятичной символики для дробных чисел.
Десятичная запись дробного числа представляет собой набор двух и более цифр от
Определение десятичной дроби
Десятичные числа представлены в виде десятичных чисел.
Например, $121,05? $ 67,9; $ 345 6700.
Десятичные дроби используются для записи обычных дробей, таких как $10, $100, $400 \ 000. Смешанные числа с дроблением, например, $10, $100, $400 \ 000.
Например, обыкновенную дробь $\frac$ можно записать в виде десятичной дроби
Чтение десятичных дробей
Десятичные дроби, которые соответствуют правильным обыкновенным дробям, читаются также как и обыкновенные дроби, только впереди добавляется фраза «ноль целых». Например, обыкновенной дроби $\frac$ (читается «двадцать пять сотых») отвечает десятичная дробь
Разряды в десятичных дробях
При записи десятичных чисел значение каждого числа зависит от его позиции. Это означает, что десятичные дроби также имеют понятие числа.
Место перед десятичной точкой называется так же, как и место перед десятичной точкой называется местом перед цифрой натурального числа. Десятичные цифры после запятой отображаются в таблице:.
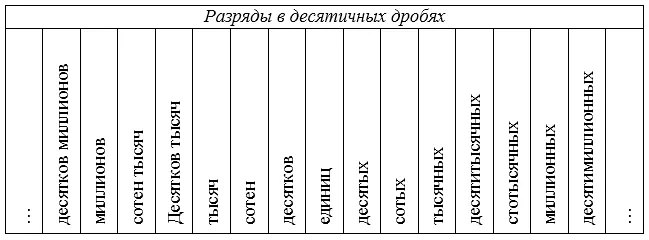
Например, в десятичной цифре $ 56 328 $, $ 5 — десятки, $ 6 в позиции 1, три десятых, $ 3 500 и $ 8 в позиции 1 000.
Десятичные числа отличаются древностью. При чтении десятичных чисел они двигаются слева направо от наиболее важного к наименее важному.
Например, десятичная дробь $ 56 328 $ высшей (наибольшей) позицией является позиция 10, а низшей (наименьшей) — тысячи.
Десятичные дроби можно анализировать в терминах натуральных или других чисел.
Например, десятичные дроби $ 37,851 $:.
.25 $ (средняя «нулевая партия 25»).
Готовые работы на аналогичную тему
Десятичные дроби, соответствующие смешанным числам, читаются так же, как и смешанные числа. Например, целое число $ 43 \ frac $ соответствует десятичной дроби $ 43,015 (что означает «43 раза целое»).
Общее число $ 405 \ frac $ соответствует десятичной дроби $ 405.08.
Максимум 9 долларов, включая так называемый \-текстит.
Например, $ 35,02 $ — $ 100,7 $ — $ 123 \ $ 456,5 $ — $ 54,89 $.
Крайняя левая цифра в десятичной записи числа не может быть нулем, исключением является только случай, когда десятичная запятая стоит сразу после первой цифры
Конечные десятичные дроби
Конечные дроби — это дроби, содержащие конечное число цифр.
Например,
Перевод обыкновенной дроби в десятичную дробь
Преобразование обыкновенных дробей со знаменателем 10 $, Ǿ точек $ в дробные числа
Прежде чем некоторые обыкновенные дроби можно преобразовать в десятичные, их нужно «подготовить». В результате такой подготовки должно получиться одинаковое количество цифр в числителе и одинаковое количество нулей в знаменателе.
Суть «предварительной подготовки» обыкновенных дробей к переводу в десятичные заключается в добавлении такого количества нулей к левой части числителя, чтобы количество цифр равнялось количеству нулей в знаменателе.
Например, подготовим обычную дробь $ \ frac $ для дробного преобразования и получим $ \ frac $. Нет необходимости готовить дробь $ \ frac $.
Сформулируем правила преобразования знаменателя $ 10, или $ 100 $, или 400 \ точек $, $ \ точек $ в десятичную дробь.
Затем сделайте десятичную партию.
Выпишите числа из числителя (при необходимости обнулите после подготовки).
Переведите правильную нормальную дробь $ \ frac $ в десятичную дробь.
Знаменатель равен $100 и содержит два нуля $3500. В числителе $ 23 и $ 3500. Это означает, что вам не нужно готовить эту дробь к десятичной дроби.
Напишите $, добавьте десятичную точку и запишите $ 23 $ от числителя. Получите десятичную дробь, $ 23 $.
Запишите правильную пропорцию $ \ frac $ в виде десятичной дроби.
Поскольку в знаменателе этой дроби $ 3 $ спряталось, в числителе $ 5 $ ноль, эту дробь нужно подготовить к преобразованию в дробь. Для этого добавьте оставшиеся нули $ 5-3 = 2 $ к числителю $ \ frac $.
Это создаст десятичную дробь. Для этого напишите $, впишите партицию и запишите число из числителя. Получите дробь 00351 $ из десятичной дроби.
Ответ: 00351 $.
Правило преобразования несправедливой дроби со знаменателем $10, $100, десятичной дроби в $ \ точки $:.
Запишите число от числителя до
делить на десятичную дробь на несколько мест вправо, так же как нули в знаменателе исходной дроби.
Преобразуйте нерегулярный нормальный процент $ \ frac $ в десятичную дробь.
Запишите число из числителя $12756 и отделите десятичные цифры $3500 справа, потому что ноль $3500 в знаменателе исходной дроби. Получите десятичную дробь $ 127,56.
, $ 138? $ 5.34 $? $ 56,123456 $? $ 350 972.54 $.
Конечные дроби можно преобразовать в обычные дроби или смешанные числа.
Например, конечной десятичной дроби $ 7,39 $ соответствует дробное число $ 7 \ frac $, а конечной дроби $ 5 $ соответствует обычная дробь $ \ frac $ (или любая дробь типа $ \ frac $ или $ \ frac.
$.
Во многих случаях десятичная точка заменяется запятой. Например, $ 35,02 $, $ 100,7 $, $ 123 \ 456,5 $, $ 54,89.
Среди многочисленных дробей, которые встречаются в арифметике, особого внимания заслуживают дроби со знаменателями 10, 100 и 1000 — короче говоря, с силой 10. Эти дроби имеют специальные названия и формы записи.
Правила записи десятичных дробей
Основное преимущество дробных дробей заключается в том, что их легко и понятно записывать. В частности.
— Это форма десятичной символики, при которой целое число отделяется от дробной части обычной точкой или стороной. Вызывается подразделение (точка или партия).
Например, 0,3 (ноль целых три десятых) — 7,25 (семь целых чисел, 25 см) — 3,049 (три целых числа, 49 мм). Все примеры взяты из предыдущих определений.
В письменной речи стороны обычно используются как десятичные знаки. Здесь и на всем этом сайте также используются партии.
Чтобы записать любую дробь в указанном выше формате, необходимо выполнить три простых действия.
- Выписать отдельно числитель;
- Сдвинуть десятичную точку влево на столько знаков, сколько нулей содержит знаменатель. Считать, что изначально десятичная точка стоит справа от всех цифр;
- Если десятичная точка сдвинулась, а после нее в конце записи остались нули, их надо зачеркнуть.
На втором этапе может не хватить чисел в числителе для завершения вытеснения. В этом случае недостающее число дополняется нулем. На самом деле, нулевые числа можно добавлять слева от любого числа без вреда для здоровья. Это не очень хорошо, но иногда полезно.
На первый взгляд, этот алгоритм может показаться очень сложным. На самом деле, это очень просто — нужно лишь немного практики. См. например:.
Задача. Для каждой дроби укажите десятичную запись.
Числитель первой дроби: 73. Если мы передвинем десятичную точку на одно место (так как в знаменателе 10), то получим 7,3.
Числитель второй дроби: 9. Сдвиньте десятичную точку на два места (так как в знаменателе 100) и получите 0,09. Необходимо было добавить ноль после десятичной точки и еще один перед ней, не оставляя странных регистраций, таких как «, 09».
Числитель третьей дроби: 10029. Сдвиньте десятичную точку на три места (поскольку 1000 находится в знаменателе) и получите 10 029.
Числитель последней дроби: 10500. верните точку с тремя цифрами — там 10 500. В конце числа находятся дополнительные нули. Удалите их — останется 10,5.
Обратите внимание на два последних примера: числа 10,029 и 10,5. согласно правилам, нули в правой части должны быть удалены, как в последнем примере. Однако ни в коем случае нельзя делать это с цифрами ноль (в окружении других цифр). Поэтому вместо 1,29 и 1,5 мы имеем 10,029 и 10,5.
Таким образом, мы разобрались с определением и форматом десятичных чисел. Затем узнайте, как преобразовывать обыкновенные дроби в десятичные и наоборот.
Переход от обычных дробей к десятичным
Рассмотрим простую дробь a/b. Используя основные свойства дробей, вы можете умножить числитель и знаменатель на число, которое в конечном итоге является степенью десяти. Однако прежде чем это сделать, прочтите следующее.
Существуют знаменатели, которые не равны 10. Вы научитесь распознавать такие дроби, поскольку с ними не справится алгоритм, описанный ниже.
Так что вот оно. Как же узнать, что знаменатель равен 10?
Ответ прост. Проанализируйте знаменатель простого множителя. Если разложение содержит только множители 2 и 5, то число можно уменьшить до степени 10. Если вы найдете другие числа (3, 7, 11 — неважно), то можете забыть о степени 10.
Работа. Проверьте, можете ли вы выразить эти дроби в виде десятичных чисел.
Опишите и проанализируйте знаменатели этих дробей.
Поэтому дроби могут быть выражены в виде десятичных чисел.
Дробь не может быть выражена в виде десятичного числа.
Это нормально; есть только числа 2 и 5. Дробь можно представить в виде десятичного числа.
Снова отображается множитель 3. Она не может быть выражена десятичной дробью.
Решив задачу для знаменателя, рассмотрим весь алгоритм перевода его в десятичную дробь.
- Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
- Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
- Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.
Конечно, дополнительные мультипликаторы можно разделить только на парные и квинтильные. Однако, чтобы не усложнять жизнь, следует выбирать наименьший возможный множитель.
И еще одно: если дробь содержит целую часть, обязательно преобразуйте ее в неправильную дробь, прежде чем применять описанный выше алгоритм.
Задача. Преобразуйте числовую дробь в десятичную дробь.
Проведите факторизацию и анализ знаменателя первой дроби. Таким образом, дробь является десятичной. В разработке есть две двойки и ни одной пятерки, поэтому дополнительный коэффициент равен количеству двоек и пятерок. У нас есть:.
Теперь перейдем ко второй дроби. Для этого обратите внимание, что дроби не могут быть выражены в виде десятичных чисел из-за триады в развитии.
Две последние дроби имеют знаменатель, равный 5 (первое число). Везде можно найти только кратные 2 и 5. В первом случае множитель 2 отсутствует, а во втором случае отсутствует множитель 5.
![]()
Переход от десятичных дробей к обычным
Обратное преобразование из десятичной в нормальную форму намного проще. Всегда можно преобразовать десятичную часть в обычный «двухуровневый» формат, поскольку нет никаких ограничений или специальных средств контроля.
Алгоритм следующий
- Зачеркните все нули, стоящие в десятичной дроби слева, а также десятичную точку. Это будет числитель искомой дроби. Главное — не переусердствуйте и не зачеркните внутренние нули, окруженные другими цифрами;
- Подсчитайте, сколько знаков стоит в исходной десятичной дроби после запятой. Возьмите цифру 1 и припишите справа столько нулей, сколько знаков вы насчитали. Это будет знаменатель;
- Собственно, запишите дробь, числитель и знаменатель которой мы только что нашли. По возможности, сократите. Если в исходной дроби присутствовала целая часть, сейчас мы получим неправильную дробь, что очень удобно для дальнейших вычислений.
Задача. Преобразуйте десятичное число в обычную дробь.
Уберите нули и запятые в левой части — получатся следующие числа (это числители):.
Первая и вторая десятичные части имеют три десятичных знака, вторая десятичная часть имеет два десятичных знака, а третья десятичная часть имеет четыре десятичных знака. Получите знаменатель.
Наконец, объедините числитель и знаменатель в обычную дробь.

Как видно из примера, полученные фракции очень часто можно уменьшить. Опять же, каждая дробь может быть выражена в виде простой дроби. Обратные преобразования не всегда выполнимы.
Такие дроби не могут быть написаны целиком, поэтому пишутся только их части, за которыми следуют недочеты. Это означает, что количество десятичных знаков бесконечно. Пример класса бесконечных десятичных дробей: 0,143346732 … ; 3,1415989032 … ; 2,666666666666666…
Как записать десятичную дробь
Посмотрите примеры написания десятичных дробей. Простое напоминание: сначала пишите целое, затем запятую, затем числитель десятичной части.
Пример 1.Преобразуйте десятичную дробь 16/10 в десятичную дробь.
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Пример 2.Преобразуйте 37/1000 в десятичную дробь.
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Как читать десятичную дробь
Важно правильно читать десятичные числа, чтобы учитель мог вас понять. Сначала добавьте слово «целый», чтобы сказать целое, затем добавьте десятичную часть с десятичной точкой. Это зависит от количества знаков после запятой.
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняйте четкость изображения для более быстрого запоминания.

Преобразование десятичных дробей
Чтобы не путать задачу с ее представлением, важно знать, как преобразовывать десятичные числа в другие виды дробей. Узнайте как!
Как перевести десятичную дробь в проценты
Уже в пятой начальной школе математика показывает, что дроби связаны с процентами. Верно: процент — это один сантиметр от любого числа, обозначается символом %.
Чтобы увидеть, как проценты преобразуются в дроби, нужно вычесть знак процента и разделить число на 100, как в примере выше.
Чтобы преобразовать дробь в проценты, умножьте дробь на 100 и добавьте знак %. Приведем пример:.
Выразить дробь в процентах очень просто. Сначала переведите в десятичные дроби, а затем примените предыдущее правило.
Чтобы ровно разрезать торт и не расстроить гостей, достаточно запомнить соотношение частей и целого. Карты — наши друзья-помощники:.
Преобразование десятичных дробей
Десятичные числа — это числа с остатком, где остаток следует за целой частью и отделяется запятой.
Смешанные дроби также являются числами с остатком, но остаток записывается как простая дробь (через дефис).
Нет необходимости изучать специальный алгоритм для преобразования дробей в смешанные дроби. Если они понимают определения и правильно читают заданные дроби, то именно это и делают учащиеся 5-го класса. Теперь давайте потренируемся!
Пример 1.Преобразуйте 5,4 в смешанные числа.
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Пример 2.Преобразуйте 4,005 в смешанные числа.
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Пример 3.Преобразуйте 5,60 в общие числа.
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Как перевести десятичную дробь в обыкновенную
Рассмотрим самый простой способ преобразования десятичного числа в обычную дробь, не изобретая велосипед. Послушайте, как это делается:.
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.








