Ну, так… У нас осталось семь слив. Но у нас больше слив, нам уже шесть лет. И каждый из нас мог бы получить сливу сверху. Тогда каждый получит три сливы вместо двух.
Что такое деление с остатком: основные правила и порядок решения
Деление с остатком — это числовое действие, при котором одно число делится на другое число, и в результате получаются два целых числа: неполный делитель и остаток. Сам остаток всегда должен быть меньше делителя. С другой стороны, если результат равен нулю во время этого действия, то делитель считается не делимым.
Следует проводить различие между делением с остатком и NAHL при выполнении числовых операций, так как это находится в строгих пределах натуральных чисел. Здесь важно помнить, что ноль не является натуральным числом. Еще один важный момент: неполный коэффициент меньшего числа, деленного на большее, должен быть равен нулю. Это несколько выходит за пределы диапазона натуральных чисел. Все эти искусственные ограничения затрудняют формулирование и дальнейшие расчеты. Балансовое деление можно выполнять не только с целыми числами, но и с другими математическими объектами. Например, с многочленами.
Дети начинают изучать деление в небольших классах. Это одно из самых важных действий, которые можно выполнить с числами. Впоследствии можно сказать, что он является основой для более сложных расчетов. В результате правила необходимо запоминать.
На первый взгляд может показаться, что сбалансированное деление никогда не пригодится в будущем. Неправда. Эта функция часто используется в компьютерных материалах и коммуникационных устройствах для получения случайных и контрольных чисел. Сама функция в разных языках программирования определяется по-разному.
Как проводится
Деление на остаток — это метод, при котором число не может быть точно разделено на различные части. Этот математический акт оставляет неделимые части, исключая целые числа.
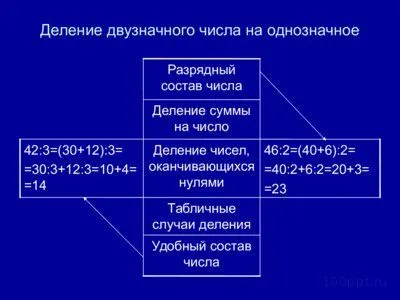
Ниже приведен простой пример, проиллюстрированный подробно.
Есть две банки по 5 литров воды и две банки по 2 литра. Когда в двухлитровую бутылку наливают воду из пятилитровой, в пятилитровой остается 1 литр неиспользованной воды. Это остаток. Численно это выглядит следующим образом:.
5:2 = 2 ОСТ (1). Откуда берется 1? 2х2 = 4, 5-4 = 1.
Рассмотрим порядок деления сбалансированных колонок. Это визуально упрощает процесс расчета.
Алгоритм определяет расположение всех элементов и порядок выполнения вычислений. Например, 17 — это 5 x 5.
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель. Основная черта обозначена оранжевым цветом.
- Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
- Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
При делении таким способом остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Если делитель больше делимого, это вызывает трудности. Дробные дроби еще не изучаются в учебном плане третьего года обучения, но по логике ответ должен быть дан в виде наихудшей простой дроби, в лучшем случае — в виде десятичной дроби. Однако (!) В дополнение к программе, метод расчета ограничен выполненной работой. Вам не нужно делить, вам нужно найти остаток! Неполная часть не является остатком! Как решить такие проблемы?
Существует правило для случая, когда делитель больше делимого: НФ равен 0, а остаток равен делителю.

Как число 5 делится на число 6? Может ли 6-литровая банка поместиться в 5 банок? Ноль, от 6> 5.
Задача состоит в том, чтобы заполнить 5 литров — нет ничего, что нельзя было бы заполнить. Это 5. После вычисления NC = 0, OST-C = 5.
Эта проблема начинается в 3 классе. До этого момента ученикам приходилось учить таблицу умножения. Это позволило им делить двузначные числа на однозначные единицы.
Решите задачу: 18 детям нужно дать 18 конфет. Сколько конфет осталось?
NC: Найдите 3*1 = 3, 3*2 = 6, 3*3 = 9, 3*4 = 12, 3*5 = 15. 5 — это слишком много. Давайте вернемся к 4.
Вам может быть интересно, почему при делении на 2 остаток равен либо 1, либо 0. Согласно таблице умножения, существует разница между делением числа на два.
Так создается расчет. Если вы внимательны и следуете правилам, нет ничего сложного. Все ученики могут научиться считать столбиками, потому что это быстро и удобно.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов разделения. Подробно об этом рассказывается в отдельной статье о делении натуральных чисел в столбик. Мы не будем повторять здесь всю теорию, а сосредоточимся на сбалансированном разделении.
Примеры будут решаться так, чтобы было легче понять реальный метод.
Пример 1.Как натуральные числа делятся в равновесии?
Разделите целое положительное число 273844 на 97.
Выполняем деление в столбик и записываем его:.
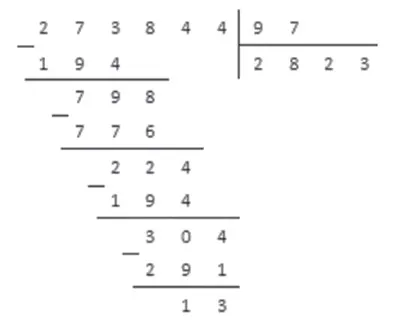
Результат: неполная часть деления равна 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти кутиент и остаток, мы можем прибегнуть к удалению делителя. Этот метод не всегда применим, но в некоторых случаях может быть очень полезен. Опять же, смотрите примеры.
Пример 2. Непрерывная абстракция наряду с балансом.
Теперь возьмите в руки семь яблок. Вы должны положить семь яблок в мешок по три яблока в каждом. Другими словами, разделите семь яблок на три.
Возьмите 3 яблока из первоначального количества и положите их в мешок. Таким образом, остается 7-3 = 4 яблока. Из оставшегося количества яблок снова извлеките 3 яблока и поместите их в другой пакет. Таким образом, они остаются 4-3 = 1 яблоко.
Одно яблоко — это остаток от деления. На этом этапе уже невозможно сформировать еще один мешок с тремя яблоками, и деление, по сути, завершено. Последствия разделения:.
Это означает, что число 3 каким-то образом дважды подходит к числу 7, причем один остаток меньше 3.
Рассмотрим другой пример. На этот раз мы приводим только математические данные, не прибегая к пропорциям.
Пример 3. Последовательное удаление в равновесии.
Число 99 больше 46, поэтому продолжите последовательное вычитание делителей.
Повторите эту функцию еще раз.
В результате, прежде чем взять остаток, необходимо было трижды отнять делимое от делителя. В результате получается меньше абстракций, чем делителей. В нашем случае остаток — это число 7.
Если делитель меньше делимого, последовательные абстракции не подходят. В этом случае ответ можно написать сразу. Неполный делитель равен нулю, а остаток равен делителю.
12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)
Следует также отметить, что что касается методов последовательной абстракции, то они полезны только тогда, когда все деление сводится к небольшому количеству вычитаний. Если дивиденд представляет собой множество делителей, использование этого метода невозможно и предполагает множество сложных вычислений.
Метод подбора неполного частного
Если натуральные числа делятся на один остаток, то результат можно вычислить, найдя неполный делитель. Покажите, как работает процесс и на чем он основан.
Сначала определим числа, необходимые для нахождения неполного делителя. Из определения делителя ясно, что делитель равен либо нулю, либо одному из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, давайте определим соотношение между делителем, делимым, не делимым и остатком. Рассмотрим уравнение d = a -b -c. Здесь d — остаток от делителя, a — делимое, b — делитель и c — квота.
В-третьих, помните, что остаток всегда меньше делителя.
Давайте вкратце рассмотрим процесс установки. С самого начала мы знаем делитель A и делитель B. Поэтому из строк 0, 1, 2, 3 и т.д. берутся числа в виде неполного квадрата c. Применяя формулу d = a -b -c и вычисляя полученное значение делителя, процесс заканчивается, если остаток d меньше делителя b. Число c на этом шаге является неполным делителем.
Используйте этот метод в примере.
Пример 4. уравновешивание и деление путем корректировки
A = 267; b = 21. Найдите неполный делитель.
Используйте тип d = a -b -c и, соответственно, измените выражение c на 0, 1, 2, 3 и т.д.
Если c = 0, то d = a -b -c = 267-21-0 = 267; число 267 больше 21, поэтому продолжите его замену.
Если c = 1, то имеем d = a -b -c = 267-21-1 = 246. После 246> 21 процесс повторяется снова.
Для c = 2, d = a -b -c = 267-21-2 = 267-42 = 225; 225> 21.
Для c = 3: d = a -b -c = 267-21-3 = 267-63 = 204; 204> 21.
Для c = 12: d = a -b -c = 267-21-12 = 267-252 = 15; 15< 21 .
На этом процесс разделения можно считать завершенным. Дробь c = 12, а остаток от деления равен 15.
Таким образом, акт деления на столбы в балансе осуществляется с помощью определенных приемов. Для этого необходимо знать точку деления одной величины на другую, тип числа и его основную награду (простое или сложное). ).
Классификация числовых величин
Точка деления — это индивидуальный критерий, по которому можно заключить деление целого числа на другое значение. Следует отметить, что числа сортируются на два типа.
Для определения первого необходимо использовать три метода: специальные таблицы, вычислительные средства и вычислительные методы. Каждая книга по математике имеет первый номер в качестве приложения. Кроме того, специальные программы можно загрузить из Интернета. Это позволяет определить, находится ли значение в первом числе или нет.
Последний метод называется ручным, так как он требует использования точки разделения для определения принадлежности значения к данной группе. Отличие простой величины от сложной заключается в том, что она может быть разделена только с одной стороны или сама по себе. Комплексные значения включают значения, эквивалентные внешнему множителю единицы.

Эксперты рекомендуют записывать точки деления на специальных картонных карточках. Все правила для двух целых чисел должны быть им понятны. Новичкам, стремящимся преуспеть в этой отрасли, следует найти примеры каждого из них, как в случае с семеркой.
Следует отметить, что создание таких «тренажеров» воспитывает память и аналитическое мышление. Затем перейдите к правилу интегрального коэффициента или делителя.
Правила целочисленного частного
В учебнике советского математика Виленкина Наума Яковлевича, утвержденном Федеральными государственными образовательными стандартами (ФГОС), содержатся правила деления одной величины на другую. К ним относятся следующие.


- На единицу и эквивалентное значение делится любая величина.
- Только четные значения, последний разряд которых заканчивается на цифры 2, 4, 6, 8, 0, могут делиться на двойку.
- Если сумма всех элементов разрядной сетки делится на тройку, то значит частное при делении на это значение будет целым.
- На четверку можно разделить величину, у которой сумма разрядов единиц и десятков делится на четыре.
- Условие деления на 5 — разряд единиц эквивалентен 0 или 5.
- Чтобы разделить искомое значение на шесть, необходимо соблюдение сразу двух условий (второго и третьего).
- Для деления величины, количество разрядов которой превышает 7, на семерку необходимо руководствоваться таким методом: разбить на группы-триады (по три), а затем просуммировать. Сумма должна делиться на 7. Если количество цифр не превышает 7, то нужно отсеять последний единичный элемент, и отнять от искомого числа удвоенный последний компонент. Результат должен делиться на 7.
- Условием деления величины на восьмерку является одновременное выполнение второго и четвертого правил.
- Чтобы разделить значение на 9, необходимо сложить все компоненты разрядной сетки. Результирующая величина при этом должна быть целочисленным значением.
- Когда последний разряд равен нулю, тогда число делится на 10.
Однако седьмое правило может показаться непонятным начинающему математику. В этом случае следует использовать пример с номером 754231897, чтобы более подробно разъяснить его реализацию. Решение заключается в следующем.
- Разбить на триады начиная от единиц: 754 | 231 | 897.
- Сложить элементы в группах: 18+6+24=48.
- Результат, полученный на втором шаге, не делится на 7 по таблице умножения (49/7=7 и 56/7=8).
Если количество имеет небольшое число цифр (273), то тип определения записывается так: 27-2 * 3 = 27-9=21. Результат показывает, что коэффициент 273 и 7 является целым числом.
Определение принадлежности чисел
Не всегда можно использовать программное обеспечение, предустановленное на мобильных телефонах или компьютерах. Для этого эксперты рекомендуют использовать метод, определяющий число как простую или сложную группу значений. Этот формат показан ниже.
Однако для демонстрации алгоритма следует провести анализ значений, эквивалентных 567. Применение выглядит следующим образом (номер шага совпадает с делителем, за исключением первого делителя)

- 567.
- (-), т. к. 7 является нечетным значением.
- 5+6+7=18 (+). Алгоритм прерывается, поскольку множитель найден.
- 567 — составная величина.
Дальнейшее нахождение множителей не может быть продолжено. Единственным исключением являются задачи, в которых необходимо найти все делители. Поскольку у нас уже достаточно базовых знаний для выполнения этой операции, мы можем перейти непосредственно к алгоритму деления с использованием остатка.
Одно яблоко — это остаток от деления. На этом этапе уже невозможно сформировать еще один мешок с тремя яблоками, и деление, по сути, завершено. Последствия разделения:.
Методика обучения детей делению столбиком
Если ученик пропускает уроки математики или не способен усваивать знания в классе, ответственность за предоставление необходимой информации лежит на родителях/опекунах. Быстрая атака на эту проблему неуместна — быстро не значит хорошо. Необходимо проявить терпение. Деление чисел легко для взрослых, но очень трудно для школьников.
Проверьте знания вашего ребенка о девяноста девяти. Если ваш ребенок не выполняет умножение «автоматически», просмотрите таблицу.
Первый пример самый простой: остаток делится на одну цифру (как показано на рисунке 1).
После того как ваш ребенок понял первое и успешно выполнил простое задание, научите его делить трехзначное число. Создайте пример 2.
Работа с многозначными числами
Задание 2: Разделите 372 на 6. Для этого сделайте на листе бумаги следующее.
- Определяем делимое (372) и делитель (6), оформляем запись в уголок:
- Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
- Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
- Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:
- В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
Пример решен, правильность можно проверить умножением: 62X6=372.
Как объяснить деление с остатком?
Бывают ситуации, когда невозможно разделить на равные доли. Самый простой способ объяснить такие ситуации ученикам — использовать простые задачи. Например.
В группе восемь учеников, и они получили 18 сырников на свои обеденные подносы. Если каждый получает по два чизкейка (18:8 = 2 и оставшиеся 2), то на подносе остается еще два чизкейка. Это остаток.
Решение для столбца с остатком описывается так же, как и для столбца без остатка, в соответствии с математическими правилами. Разница лишь в том, что остаток — последний. В этом варианте правильно писать количество целых единиц и количество оставшихся единиц (например, четыре в целых оставшихся единицах и девять в оставшихся).
Учеников следует обучать постепенно, от простых примеров к более сложным. Если они не знают простых действий деления, информацию следует повторить. Постепенно решение примеров будет становиться все быстрее и безопаснее. Главное — доверять способностям малышей, набраться терпения, и деление чисел методом столбика может стать увлекательным занятием для школьников.








