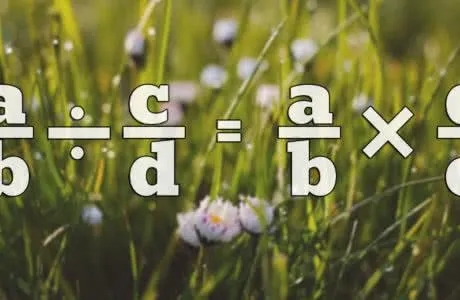Если коэффициент деления двух чисел является многозначным числом, то оно делится в столбик. Это также известно как угловое деление.
Получить целое число при делении
В этой статье мы рассмотрим разделение полноты без баланса. Мы будем обсуждать деление чисел целостности только в тех случаях, когда абсолютные числа делятся поровну (см. Деление чисел целостности без равновесия). В отдельной статье мы обсудим деление целых чисел, которые уравновешивают друг друга.
Сначала представлены термины и символы, используемые для описания деления интегралов. Далее вводится понятие расщепления чисел целостности. Это помогает извлечь правила для разбиения положительной полноты, отрицательных целых чисел и целых чисел с разными знаками. В этом разделе также рассматривается пример применения правил разбиения к целым числам. Наконец, мы показываем, как контролируются результаты расщепления последовательности.
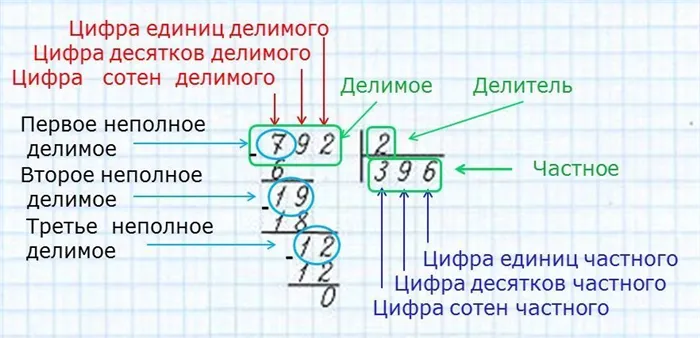
Термины и обозначения
Для описания деления целых чисел мы используем те же термины и символы, что и при описании деления натуральных чисел (см. разделение, разделы, части и деления). Позвольте нам напомнить вам.
Делимое целое число называется делителем. Делимое целое число называется делителем. Результат деления целого числа называется делителем.
Деление обозначается символом: между дивидендом и дивидендом (иногда встречается символ, указывающий на деление). Деление целого числа a на целое число a можно записать символом: a:b. Если целое число a приводит к числу C, исключая целое число B, то удобно записать этот факт в виде равенства: выражение b = C вида a:b также называется квантором, как и значение выражения.
Смысл деления целых чисел
Мы знаем о существовании связи между умножением и делением натуральных чисел. Из этой связи мы делаем вывод, что деление — это нахождение неизвестного множителя, когда второй множитель и произведение известны. Давайте придадим такое же значение разделению последовательности. Другими словами, деление последовательности — это одно целое число определенного произведения и другой целочисленный множитель.
Исходя из понятия последовательного деления, можно сказать, что если произведение двух целых чисел a и b равно c, то при делении c на a получается b, а при делении c на b — b. Пример. Допустим, мы знаем, что произведение двух целых чисел 5 и -7 равно -35, мы можем сказать, что коэффициент (-35) : 5 равен -7, а коэффициент (-35) : (-7) равен 5.
Обратите внимание, что коэффициент деления целого числа a на целое число b является целым числом (если A делится на B без остатка).
Результат этого действия считается бесконечно большим и бесконечно равным. Смысл этого выражения заключается в том, что коэффициент бесконечно возрастает (по модулю), если делитель приближается к нулю, а делимое остается равным или близким к A.
Содержание

Целочисленное кольцо не замкнуто на деление. Проще говоря, это означает, что результат деления целого числа на другое целое число может быть нецелым. Однако если результатом является целое число, то говорят, что это деление без остатка.
Деление чисел долгое время считалось самой сложной арифметической операцией. В Средние века мало кто знал «секрет» деления. Это было связано с тем, что существовавшие алгоритмы деления были очень громоздкими и сложными для выполнения и запоминания (например, деление в виде лодочек). С появлением колонного деления ситуация радикально изменилась. Деление, наряду с другими арифметическими действиями, теперь входит в программу по математике для первого класса школы. Однако, как и в случае с умножением (см. Быстрое умножение), недавно был открыт более эффективный алгоритм для вычислительных целей (см. en: Деление (цифровое)).
Существуют правила, позволяющие быстро определить, делится ли число на определенный делитель без остатка (точка деления). Наиболее известными делителями являются 2, 3, 4, 5, 8, 9, 11, 25 и их производные, а также делители 7, 13, 1001 и других чисел.
Целое число, которое одновременно делится на много чисел без остатка, называется наибольшим общим делителем.
Определение количества делителей натурального числа приводит к двум важным понятиям: комплексные числа и простые числа. Простое число имеет два различных делителя: единицу и само число. Комплексные числа имеют три или более различных делителей. 1 не является ни комплексным, ни простым числом.
Если натуральное число не делится на другое число без остатка, его иногда называют делением с остатком. Изучение остатков, их сравнение и стандартизация в выводе привели к созданию целой науки — теории чисел.
На остатки обычно накладываются следующие ограничения (чтобы они были правильно определены, т.е. уникальны).
где — делитель, а — остаток.
Деление целых чисел
Деление на любое целое число по сути ничем не отличается от деления на натуральные числа. При условии, что единицы измерения разделены и учтена конвенция знаков.
Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например,
Деление рациональных чисел
Замыкание множества целых чисел действием деления расширяет множество логических чисел. Это приводит к тому, что результат деления целого числа на другое целое число всегда является рациональным числом. Более того, полученные числа (рациональные числа) уже полностью поддерживают акт деления (они замкнуты на него).
Правила деления логических дробей: = \ frac = \ frac «ширина =» «» высота = «» />
Если известно количество учеников в классе и количество яблок, взятых каждым из них, то общее количество яблок можно вычислить, умножив количество учеников на количество яблок, взятых каждым из них. Другими словами, количество учеников — это первый фактор, количество яблок — второй фактор, а количество розданных яблок — произведение.
Конкретный смысл действия деление. Название чисел при делении
Минус сказал, что он посетил ГД. Там они кормили голодных кошек и распределяли пойманную рыбу поровну между ними. Таким же образом они ели соседских детей, а также груши. Они решали различные задачи на деление и объясняли, когда нужно делить с минусом.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный кабинет.
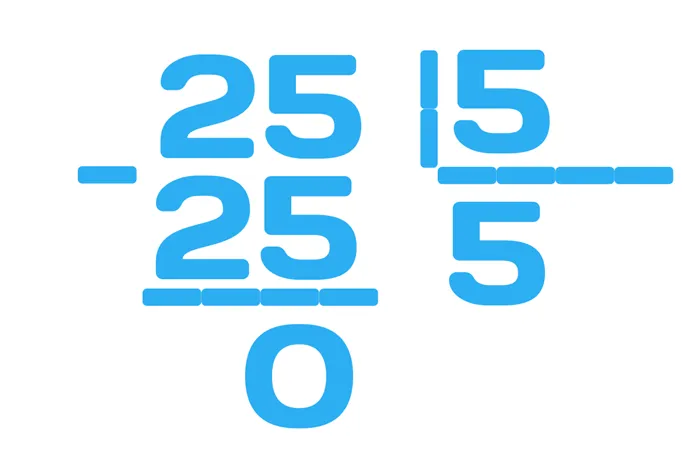


Конспект урока «Конкретный смысл действия деление. Название чисел при делении»
Добрый вечер!!! Я скучал по вам, ребята. Я поехал в отпуск к родственникам. А Плюс был здесь совсем один. Но теперь пришло время отдохнуть. О, все будет хорошо. r
И сегодня я представляю вам новое поведение — ядерное деление. Именно так зовут моего родственника — Ядерное Деление. Он очень добрый. Мы вместе сделали много хорошего. Недалеко от жизни, которую мы разделяем, живет бездомная кошка. Поэтому каждый день мы ловили рыбу и приносили еду. В первый день мы поймали восемь рыб и пошли кормить кота. Кошки подбежали к нам, и мы дали им две рыбки. Как вы думаете, сколько кошек мы накормили в первый день?
Посмотрите, как это произошло. Первый кот побежал и взял две рыбы, затем следующий кот. Он поймал еще две рыбы, затем еще одна кошка поймала две рыбы. И последняя кошка, к которой он подошел, была маленькая рыжая, и он тоже поймал две рыбы. А наше ведро было пустым.
Все котята взяли по две рыбки. Сколько раз ты дал каждому из них по две рыбки? Один, два, три и четыре. Поэтому мы подарили им четырех кошек.
На следующий день мы поймали четырнадцать рыб. Мы накормили кошек и рыбу и подумывали о том, чтобы съесть оставшуюся рыбу. Но на этот раз у нас было больше кошек. Поэтому мы стали кормить двух рыбок равными порциями каждую, пока ведро снова не освободилось. Сколько кошек мы накормили в этот раз?
Поэтому, используя цифры и математические символы, мы записывали, как мы кормили кошек.
Да, это хорошо. Семь раз происходит акт удаления. Другими словами, семь котят ели рыбу.
Но на третий день мы пошли на рыбалку рано утром, и мы поймали котенка, и это был хороший котенок, и это был хороший котенок, и мы поймали его. И мы поймали, вы не поверите — 48 рыб. Но на этот раз пришло целое стадо кошек и все съело. Хотите посчитать, сколько кошек бегает?
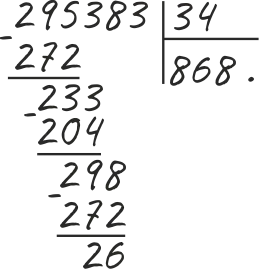
Ну, мы боимся смотреть на снимки. Конечно, мы измерили 24 кошки. Но это очень позорный рекорд. И здесь мне на помощь пришел сектор, который является моим родственником. Если все удаления на самом деле одинаковы, т.е. если что-то распределено поровну и ответ равен нулю, то это действие можно заменить делением. Результат — количество абстрактных факторов.
Посмотрите, как кормили кошку в первый день:.
Затем мы измерили, сколько раз кошке давали рыбу, т.е. два числа. Вместо того чтобы входить в систему таким образом, вы можете делать более короткие записи. Сначала мы пишем число, обозначающее общее количество рыб. Мы пропускаем ячейку и пишем число, указывающее, сколько рыб получил каждый кот. А между ними мы помещаем символ разделения:.
Видите, это мое относительное разделение, а это символ разделения — две точки.
А теперь читаем запись: восемь делится на два получается 4. Поэтому я поставил четырех кошек.
А как вы поделили 14 рыб между кошками:.
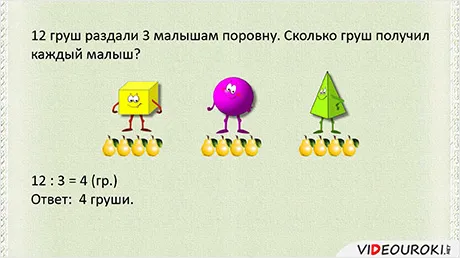
Рядом с адресом живут три малыша — Кубик, Шарик и Пирамидка. При делении они часто превращаются в плоды. А вчера, пока я не пришла домой, мы купили 12 груш и раздали всем поровну. Вы думаете, каждый человек получил его?
Давайте посмотрим, как распределились груши. Вот 12 груш. Сначала каждому ребенку давали по одному, потом еще и еще. Груши готовы. Мы распределяем 12 груш поровну между тремя детьми.
Разделения могут контролироваться подразделениями, если действие разделения не приводит к равновесию. Действительно, если делитель является произведением делимого и делителя, нам нужно взять второй коэффициент, делитель, разделив делимое на делитель (один из коэффициентов).
Деление 3 класс
Дети в третьем классе только начинают проходить через разделение. Поэтому студенты третьего курса решают самые простые задачи.
Задача 1. Работник фабрики обещает положить 56 пирожных в 8 упаковок. Сколько пирожных должно быть в каждой упаковке, чтобы положить в каждую упаковку одинаковое количество пирожных?
Вопрос 2: В канун Нового года классу из 15 детей в школе раздают 75 конфет. Сколько сладостей должен получить каждый ребенок?
Вопрос 3. Роман, Саша и Миса выбрали 27 яблок с одной яблони. Сколько яблок получит каждый, если им придется делиться поровну?
Вопрос 4. Четыре друга купили 58 печений. Но потом они поняли, что не могут разделить их поровну. Сколько еще печенья нужно, чтобы каждый друг получил 15 печений?
Деление 4 класс
Деление на четвертый класс более серьезное, чем на третий. Все расчеты производятся путем разбиения на столбцы, и число, входящее в разбиение, немаленькое. Что такое разделение колонок? Ответ вы найдете ниже:.
Деление в столбик
Найди ответ на свой вопрос Что такое деление в столбик? Это способ поиска ответов для деления больших чисел. Если вы можете разделить такое простое число, как 16 или 4, то ответ очевиден — 4. Тогда 512:8 в детском сознании не так-то просто. Наша задача — рассказать о методах решения таких примеров.

Шаг 1. Напишите делитель и делимое следующим образом.
В итоге части записываются под делителем, а вычисление — под делимым.
Шаг 2. Начните делить слева направо. Во-первых, возьмите число 5.
Шаг 3. Пятая цифра меньше восьмой и поэтому не может быть разделена. Таким образом, получается еще одна цифра делителя.
51 теперь больше 8. Это неполный коэффициент.
Шаг 4. Поставьте точку под разделителем.
Шаг 5. За 51 следует 2, поэтому ответом будет другое число. Другими словами, коэффициент — это двузначное число. Поставьте вторую точку:.
Шаг 6. Запустите режим разделения. Максимальное число делителей от 8 до 51 без остатка равно 48; деление 48 на 8 дает 6. Напишите 6 вместо первой точки под делителем.
Шаг 7. Затем напишите число чуть ниже 51 и добавьте знак ‘-‘.
Шаг 8. Затем вычтите 48 из 51, чтобы получить ответ 3.
Шаг 9*. Вычтите число 2 и запишите его рядом с числом 3.
Шаг 10 Разделите полученное число 32 на 8, чтобы получить вторую цифру ответа — 4.
Ответ — 64, что не является сбалансированным. При делении на 513 остаток равен 1.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления столбиком, описанным в примере выше. Это пример трехзначного числа.
Деление дробей
Деление не так сложно, как может показаться на первый взгляд. Например, (2/3): (1/4). Метод деления прост. 2/3 — делитель, а 1/4 — делимое. Знак деления (:) может быть заменен знаком умножения (), но для этого позиции числителя и знаменателя делителя меняются местами. Таким образом, мы имеем (2/3) (4/1), (2/3) * 4, что равно 8/3 или 2 целых числа и 2/3. Вот еще один пример с диаграммой для лучшего понимания. Изучение дробей (4/7):( 2/5):.
Как и в предыдущем примере, делитель 2/5 инвертируется для получения 5/2, а делитель заменяется умножением. Таким образом, получаем (4/7)*(5/2). Вычтите и ответьте: 10/7, затем вычтите целую часть: 1 целое число и 3/7.
Деление числа на классы
Введите число 148951784296 и разделите на 3 цифры: 148 951 784296. Таким образом, справа налево: 296 — класс единиц, 784 — класс тысяч, 951 — класс миллионов, 148 — класс миллионов. миллиарды. Аналогично, каждый класс имеет три разряда со своим разрядным классом. Справа налево: первая цифра — единицы, вторая цифра — десятки, третья цифра — сотни. Например, порядок единиц — 296, 6 — единицы, 9 — десятки и 2 — сотни.
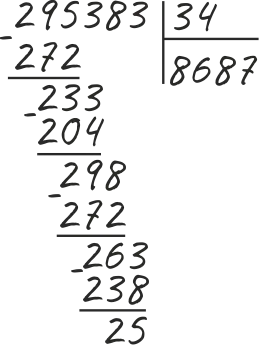
Вопрос 2: В канун Нового года классу из 15 детей в школе раздают 75 конфет. Сколько сладостей должен получить каждый ребенок?
Рассмотрим пример: 6:2 = 3, умножаем на 2σ3= 6, чтобы проверить, правильно ли вы разделили. Примечание 3:0 является неконтролируемым, так как любое число, умноженное на ноль, будет равно нулю. Поэтому примечание 3:0 не имеет смысла. Правило деления: нельзя делить на ноль.
0: 3 = 0 Это письмо имеет смысл. Если ничто разделить на три, то не будет ничего. 0: a = 0 Правило деления: если 0 делится на натуральное число, не равное нулю, то результат всегда равен нулю.
3: 3 = 1 a: a = 1 Правило деления: при делении любого числа, не равного нулю, на само себя результат всегда равен 1.
Вопрос по дивизиону:.
С помощью символики a: b = c, каков здесь коэффициент? Ответ: a: b и c.
Каков здесь коэффициент? ОТВЕТ: Коэффициент показывает, во сколько раз делимое больше делителя.
Что символизирует 0⋅m= 5? Ответ: При умножении на ноль ответ всегда равен нулю. Записи бессмысленны.
Существует ли n такое, что 0⋅n= 0? Ответ: Да, запись имеет смысл. Если умножить любое число на ноль, то оно станет нулем. Следовательно, n — произвольное число.
Пример №1: Найти значение выражения: а) 0:41 б) 41:41 в) 41:1 Ответ: а) 0:41 = 0 б) 41:41 = 1 в) 41:1 = 41
Пример 2: Исходя из значений переменных, применимо следующее уравнение: a) x: 6 = 8 b) 54: x = 9
(a) В данном примере x — это линия раздела. Чтобы найти дивиденд, умножьте делимое на делитель. x — неизвестный делитель, 6 — делимое и 8 — делитель. x = 8⋅6x = 48
(b) 54 — делитель, x — делимое и 9 — делитель. Чтобы найти неизвестный делитель, разделите делимое на делитель. x = 54: 9 x = 6
Задача 1: У Саши 15 марок, а у Мисс — 45. На сколько марок больше у Мисс, чем у Саши? Решение: проблема может быть решена двумя способами. Первый способ: 15+15+15 = 45 Чтобы получить 45, нужно 3 числа 15. Таким образом, масса имеет в 3 раза больше марок, чем Саша. Второй метод: 45:15 = 3
ОТВЕТ: у массы в три раза больше марок, чем у Саши.
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.