$ 3.5: 1.8 =.<35\over<10>>:<18\over<10>> = \ over> =.<35\over<18>> $ — это все расчеты. Иногда необходимо разделить десятичное число на столбики. В этом случае проще использовать и этот метод.
Деление десятичной дроби на натуральное число
Чтобы разделить десятичное число на натуральное, необходимо
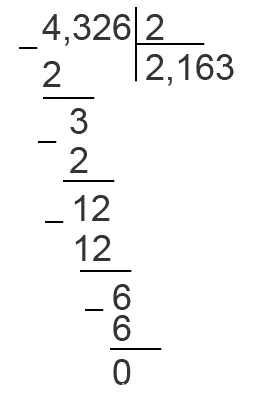
Разделите пропорцию на это число без учета сторон. После того, как вы закончили деление целой части и вам нужно убрать число после партии, поместите партию в коэффициент.
Если целое число меньше делителя, то ответ начинается с нулевого целого числа.

Деление на десятичную дробь
Чтобы разделить число на десятичные дроби, необходимо
- Избавиться от запятой в делителе. Для этого в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
- После этого выполнить деление на натуральное число.
Разделите 12.096 на 2.24. Для любого номера переместите две цифры вправо. Вы получите 1209.6 и 224. Разделите их один на другой.
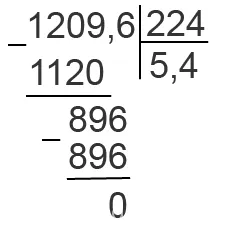
12,096:2,24 = 1209.6:224 = 5.4

Разделите 4,5 на 0,125. Переместите партию на три места вправо как к делителю, так и к делимому. Добавьте два нуля справа, поскольку 4,5 имеет только одну цифру после десятичной точки. Получите 4500 и 125. Разделите на столбцы.
4,5: 0,125 = 36, как в 4500: 125 = 36.
Разделите 25 на 0,05. Сторона должна быть перенесена на делитель, а делитель должен быть перенесен на два места вправо. Но 25 — это целое число, а как насчет сторон? Каждое целое число может быть записано в виде партий, за которыми следует то, что вы хотите. 25 = 25.00. сдвиньте сторону на две цифры, чтобы получить 2500.
Деление десятичной дроби 0,1; 0,01; 0,001 и т.д.
Разделите число на 0,1, 0,01, 0,001 и т.д. — Это то же самое, что и умножение на 10, 100, 1000 и т.д. Для этого переместите партию на делитель так далеко вправо, как ноль находится в делителе перед единицей (ноль перед партией также учитывается).
Если чисел недостаточно, то сначала нужно добавить несколько нулей в конец дроби.
См. схему ниже. Здесь показано, где писать делитель, делимое, коэффициент, остаток и промежуточные вычисления при делении дробей в столбик.
Деление с целыми числами
Вы можете сохранить деление целого числа на дробь десятичной дроби или наоборот.
При делении всегда следует учитывать, хотите ли вы получить результат в дробной или десятичной форме. Другими словами, вы можете получить результат, записанный в виде строки или дроби.
Давайте рассмотрим оба варианта, начиная с целых чисел.
Чтобы вызвать дробь в качестве результата деления, делитель и делимое должны быть дробями. Давайте разделим 18 на 1,9.
Что такое 18? Доля доллара.<18\over<1>> $. Результат — 400,9 =.<19\over<10>> $
Когда дробь делится, дроби деления меняются местами, а получившиеся дроби перемножаются.
В дробях тире обозначает символ деления. Это свойство очень часто используется в преобразованиях и расчетах, поэтому его важно знать.
При делении в столбик следует учитывать, что всякий раз, когда остается неделимый остаток, необходимо добавить стороны, а для продолжения деления — нули. Это конкретное число может быть бесконечным, но будет достигнуто немного позже.
Что делать, если нужно разделить целое число на десятичные единицы, используя подходящий или неправильный десятичный конечный результат? Вам нужно умножить делитель на делимое и разделить на 10. Этот процесс в математике называется смещением запятых.
Для 72:3,6 = 720:36 = 20 -0,36 необходимо умножить на 100.
Сигнальное правило умножения также применимо к делению. Отрицательные числа, деленные на отрицательные числа, приводят к положительным числам. Позитивные позитивы также позитивны. Однако при делении положительного числа на отрицательное или наоборот получается отрицательное число.
Вам не нужно бояться больших результатов. Это нормально и более чем правильно. При делении целого числа на десятичную дробь, если дробь правильная, результат должен быть больше делителя. Правильная дробь — это дробь, меньшая единицы.
Деление с дробными числами
То же самое справедливо и для дробей. Основная проблема — страх перед дробями. Деление целых чисел на дроби не кажется большой проблемой, но почему-то ученики неоправданно боятся деления дробей на дроби.
Чтобы обойти это, просто переместите партию.
$ 3,8:0,5 = $ 38:5 — и правило несбалансированного деления работает.
Процесс еще более упрощается, если вдруг желаемый результат нужно записать в дробях. Таким образом, дивиденд переносится в числитель, а делитель — в знаменатель. Внимательно следите за конверсиями и не пропускайте ни одной партии.
$ 3.5: 1.8 =.<35\over<10>>:<18\over<10>> = \ over> =.<35\over<18>> $ — это все расчеты. Иногда необходимо разделить десятичное число на столбики. В этом случае проще использовать и этот метод.
Бесконечные числа
Неприятная ситуация может возникнуть, если результат вычисления окажется бесконечным. К таким числам относятся числа с бесконечным числом знаков после запятой. Вспомните уже упомянутые примеры.
$ 18:1.9 = 180:19 = 9.473684 … $ — и, следовательно, возможность перехода к бесконечности. Кстати, такие числа можно встретить и в точных расчетах. Например, пи часто принимают за 3,14, хотя на самом деле это бесконечность. Он еще не полностью рассчитан. Более того, десятичная точка этого числа повторяется без каких-либо определенных параметров, что является одной из загадок математики.
Что вы должны делать в таком случае? Запишите его в виде дроби или округлите, если позволяет задача.
Если цифра перед округленным значением меньше 5, то значение не изменяется. В противном случае значение округляется в большую сторону на 1.
$ 18:1.9 = 180:19 = 9.473684 … = $ 9,47 — в большинстве случаев цена округляется до ближайшего сантиметра.
Если учащимся необходимо выучить основные правила деления десятичных чисел, следует отметить, что популярные сегодня калькуляторы дают надежные ответы. Без них решение проблем может стать проблемой. Однако если вы правильно объясните ребенку предмет, он быстро освоит самые сложные области математики.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
Лучший способ объяснить, как делить колонки, — это использовать примеры. Расчет:.
Начните с записи делителя и делимых в столбик. Это будет выглядеть следующим образом
Запишите делитель (результат) под делителем. В нашем случае это номер 8.
1 Определите неполный делитель. Сначала посмотрите на первую цифру слева от делителя. Если число, определяемое этой цифрой, больше делителя, обработайте его в следующем разделе. Если число меньше делителя, необходимо добавить следующую цифру слева от делителя и обработать число, определяемое этими двумя цифрами. Для удобства укажите номер для работы в списке. 2.2.
2 Возьмите 5. 5 меньше 8, поэтому из делителя нужно взять еще одну цифру. 51 больше 8 и поэтому является неполным делителем. Поставьте точку на делителе (под углом делителя).
После 51 остается только одна цифра — 2. Поэтому добавьте к результату еще одну точку.
Теперь вспомните 99 из 8 и найдите произведение, близкое к 51 → 6 x 8 = 48 → впишите 6 в коэффициент.
Запишите 48 под 51 (умножение делимого на 6 и делителя на 8 дает 48).
Предупреждение.При записи под неполным коэффициентом правая цифра предсердного коэффициента должна быть выше цифры справа от произведения.
4. между 51 и 48 поставьте знак «-» (минус) с левой стороны. Удалите 48, используя правило удаления, и запишите результат под чертой.
Однако, если результат удаления равен нулю, не пишите его (если только удаление в этот момент не является последним шагом для завершения процесса разделения столбцов).
Баланс — 3. Сравните остаток с делителем. 3 меньше 8.
Предупреждение. Если остаток больше делителя, значит, мы вычислили неправильно и имеем произведение, близкое к полученному.
5.Далее запишите это число в той же колонке файла делителей, под горизонтальной чертой справа от стоящего там числа (или справа от точки, где вы не написали ноль). Если в этом столбце нет числа в обозначении делителя, то деление столбца на этом заканчивается.
Число 32 больше 8. Используйте таблицу умножения еще раз с 8, чтобы найти ближайшее произведение -> 8 x 4 = 32:.

Баланс равен нулю. Это означает, что числа разделены поровну (нет баланса). Если последнее удаление заканчивается нулем и больше нет цифр, то это остаток. Добавьте к коэффициенту скобки (например, 64 (2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число выполняется аналогичным образом. Таким образом, первый «промежуточный» дивиденд делится на старший разряд, который должен быть больше делителя.
Например, в 1976 году деление было разделено на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов – 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов – 197.
- Число 197 больше 26, делим 197 десятков на 26: 197 : 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.
- 156 делим на 26, получаем 6.

Если на каком-либо этапе деления «промежуточный» делитель окажется меньше делимого, в делитель записывается 0, а число из этой цифры записывается в следующую меньшую цифру.
Деление с десятичной дробью в частном.
Если целое положительное число не делится на одно угловое положительное целое число, его можно продолжать делить на число и получать дробь от получившейся десятичной дроби.
Например, 64 делится на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.

Таким образом, если при делении положительного целого числа на положительное уникальное или кратное число получается остаток, вы можете поместить партицию на цитату, преобразовать остаток в следующую меньшую единицу числа и продолжить деление.
Если учащимся необходимо выучить основные правила деления десятичных чисел, следует отметить, что популярные сегодня калькуляторы дают надежные ответы. Без них решение проблем может стать проблемой. Однако если вы правильно объясните ребенку предмет, он быстро освоит самые сложные области математики.
Бесконечные числа
Неприятная ситуация может возникнуть, если результат вычисления окажется бесконечным. К таким числам относятся числа с бесконечным числом знаков после запятой. Вспомните уже упомянутые примеры.
$ 18:1.9 = 180:19 = 9.473684 … $ — и, следовательно, возможность перехода к бесконечности. Кстати, такие числа можно встретить и в точных расчетах. Например, пи часто принимают за 3,14, хотя на самом деле это бесконечность. Он еще не полностью рассчитан. Более того, десятичная точка этого числа повторяется без каких-либо определенных параметров, что является одной из загадок математики.
Что вы должны делать в таком случае? Запишите его в виде дроби или округлите, если позволяет задача.
Если цифра перед округленным значением меньше 5, то значение не изменяется. В противном случае значение округляется в большую сторону на 1.
$ 18:1.9 = 180:19 = 9.473684 … = $ 9,47 — в большинстве случаев цена округляется до ближайшего сантиметра.
При делении в столбик следует учитывать, что всякий раз, когда остается неделимый остаток, необходимо добавить стороны, а для продолжения деления — нули. Это конкретное число может быть бесконечным, но будет достигнуто немного позже.
Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Разделение десятичных дробей на столбцы немного сложнее, чем разделение целостности, так как оно используется в мобильных устройствах по умолчанию и требует разделения баланса. Поэтому при необходимости упрощения процесса или проверки результатов можно использовать электронный калькулятор. Здесь будет показан весь процесс, а также ответы.
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
Существует множество онлайн-сервисов, подходящих для этой цели, но почти все они не сильно отличаются друг от друга. Сегодня мы подготовили два разных способа сделать это, и вы можете выбрать тот, который лучше всего подходит для ваших нужд, прочитав инструкцию.
Сайт Onlinemschool был разработан для того, чтобы помочь вам в изучении математики. Помимо того, что он содержит много полезной информации, курсов и заданий, он также построен на основе калькулятора, которым вы пользуетесь в настоящее время. Вот как разделить десятичное число
-
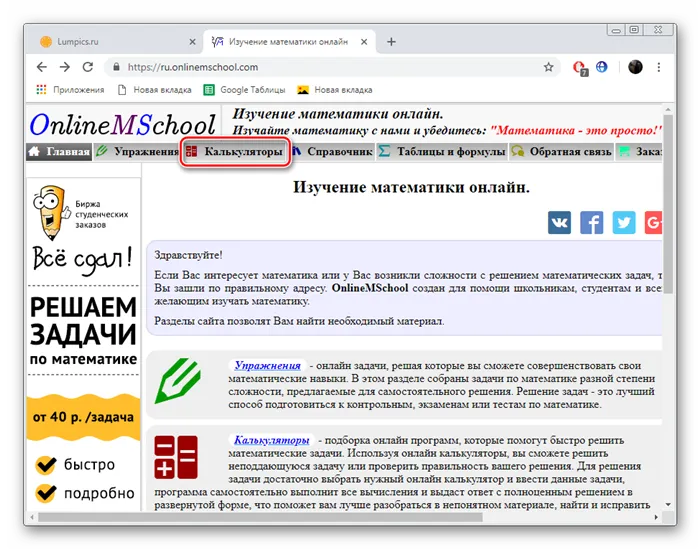
Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
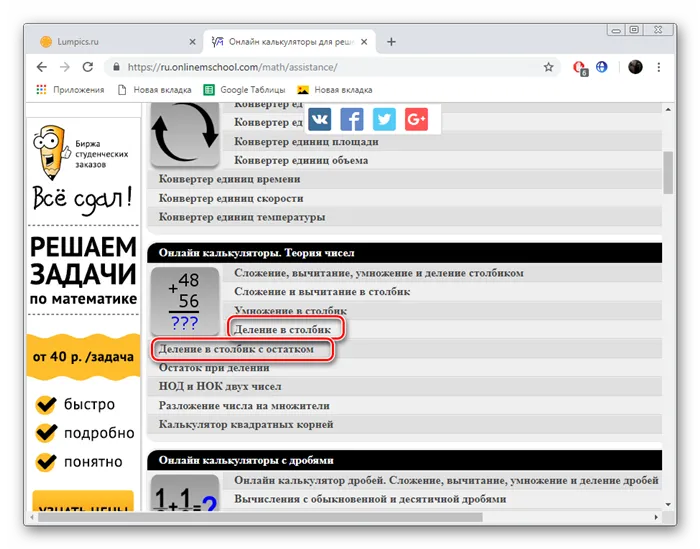
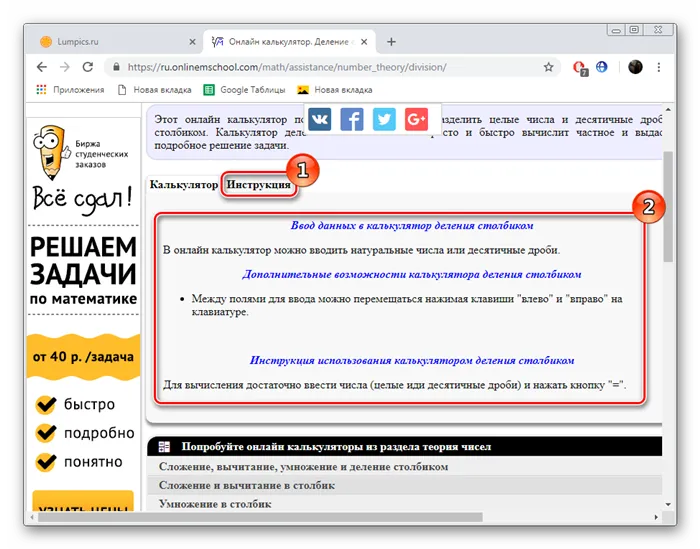
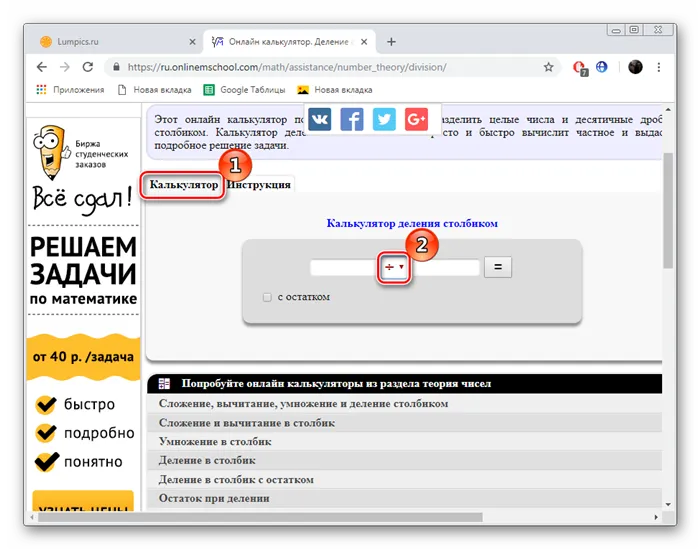
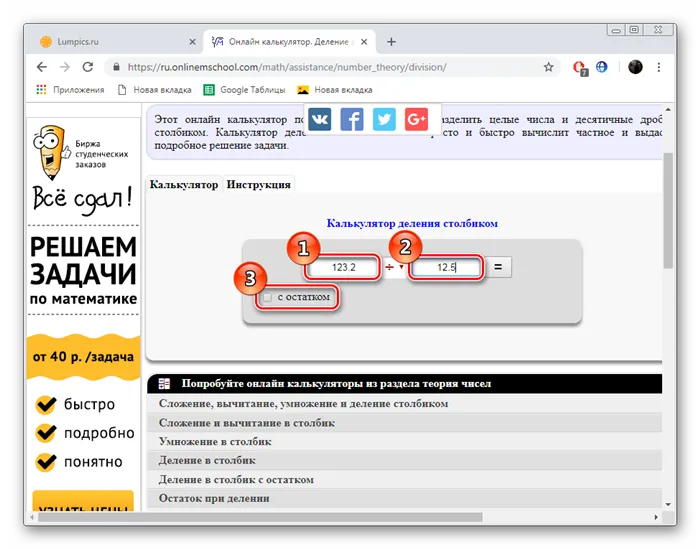
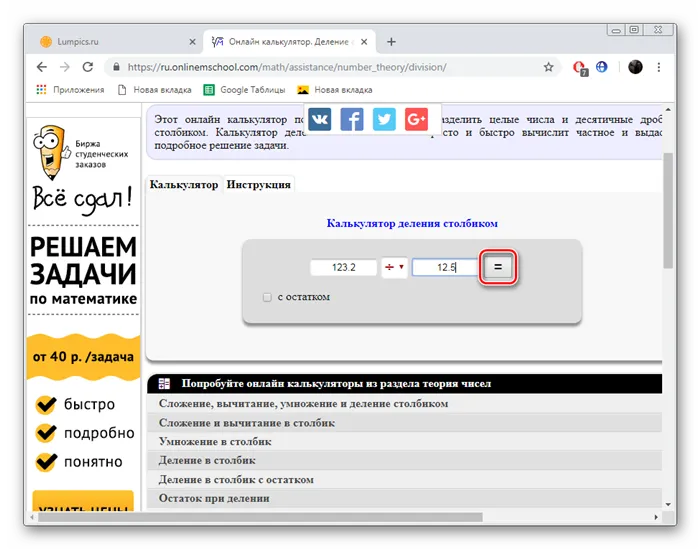

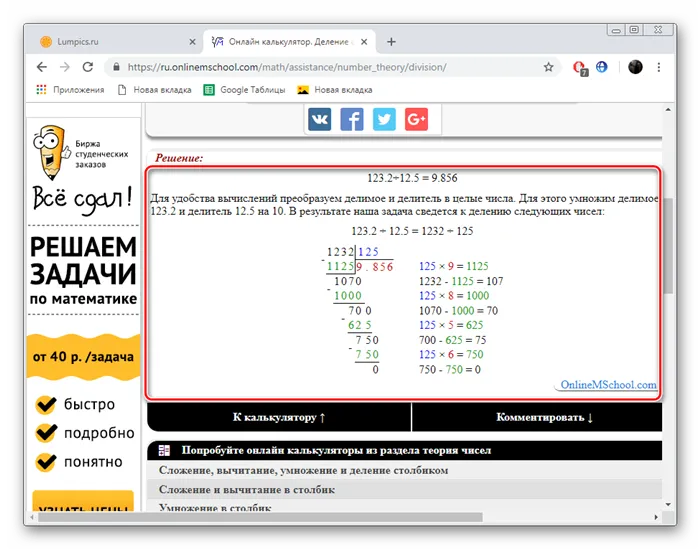
Внимательно изучите состояние проблемы, прежде чем делиться балансом. Часто в этом нет необходимости, иначе ответ может оказаться неверным.
Всего за семь простых шагов с помощью небольшого инструмента от Onlinemschool можно разделить десятичную дробь на столбцы.
Способ 2: Rytex
Онлайн-сервис Rytex также может помочь вам в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует его калькулятор. Это можно использовать следующим образом.
-
Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи «Онлайн калькуляторы».
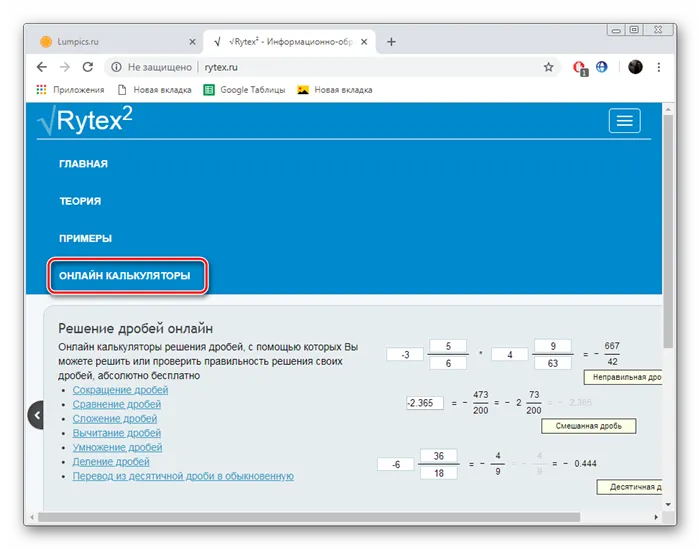
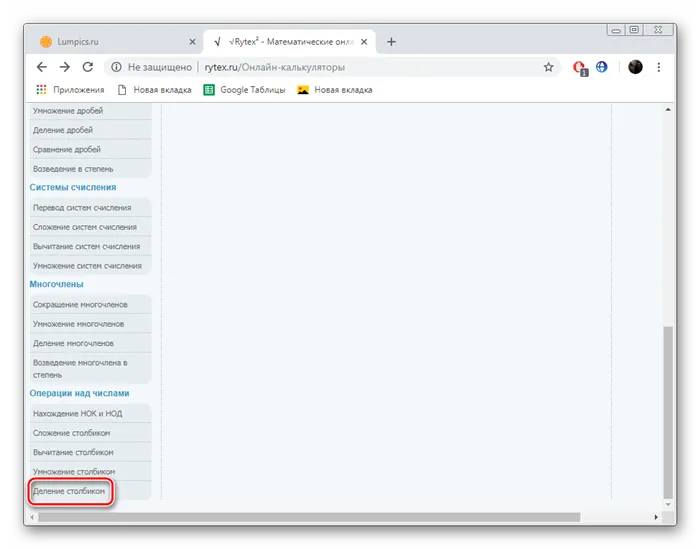
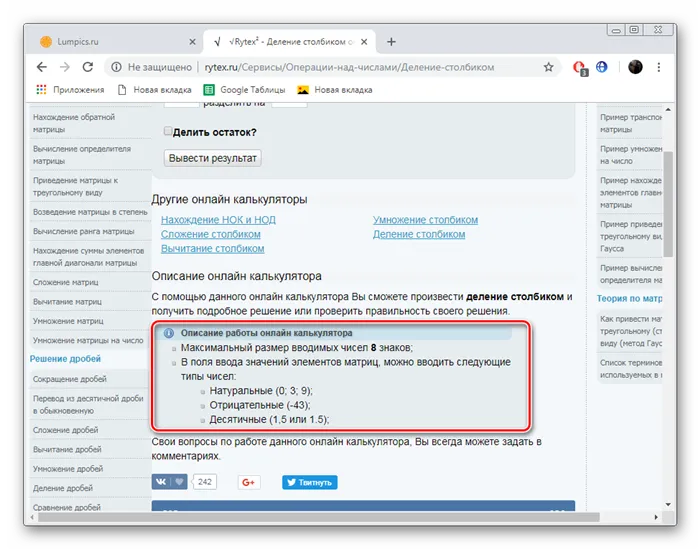
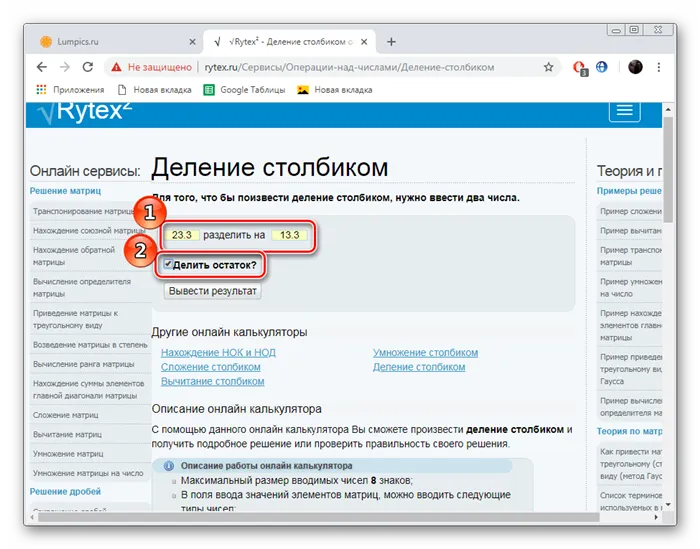
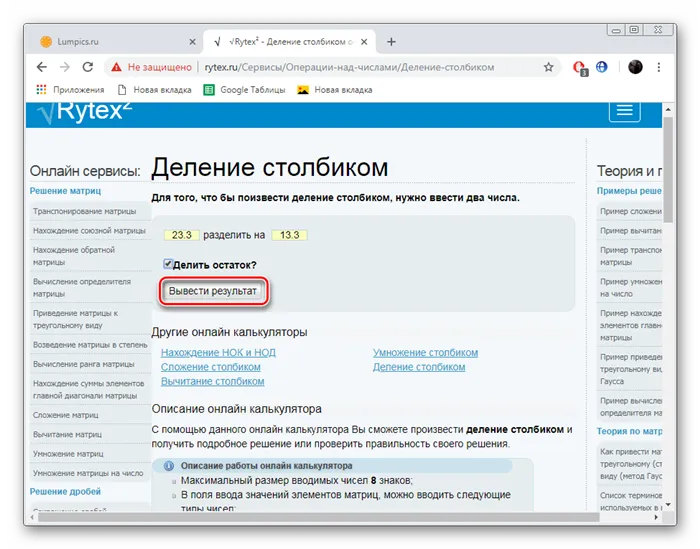
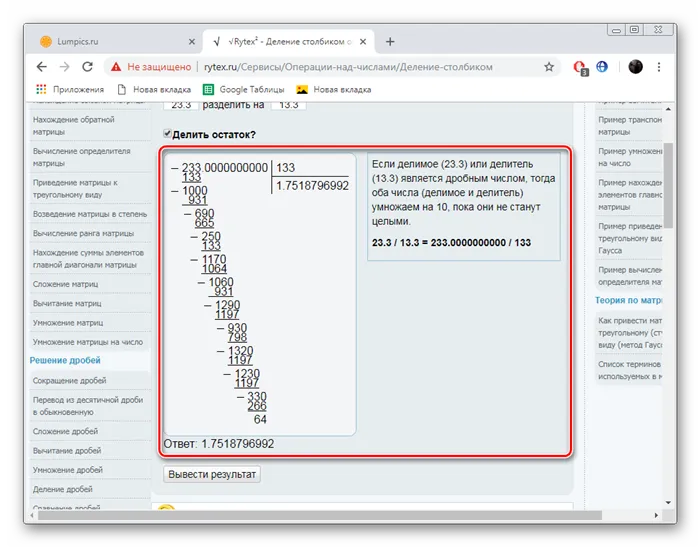
Как видите, рассматриваемые нами услуги практически идентичны друг другу, за исключением их внешнего вида. Таким образом, можно сделать вывод — нет никакой разницы, каким онлайн-источником вы пользуетесь. Все калькуляторы рассчитывают правильно и дают подробные ответы на примеры.
Мы рады, что помогли вам решить вашу проблему, и надеемся, что наша помощь будет вам полезна.
Помимо этой статьи, на сайте есть еще 12866 полезных инструкций. Добавьте lumpics.ru в закладки (ctrl+d) и вы окажетесь там.








